Lecture 1 5 Hierarchy Theorem Space Hierarchy Theorem

Lecture 1 -5 Hierarchy Theorem

Space Hierarchy Theorem

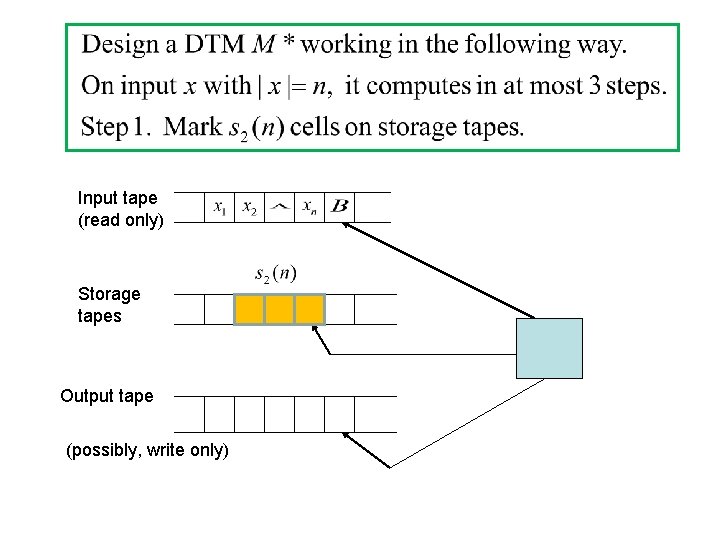
Space-constructible function • s(n) is fully space-constructible if there exists a DTM M such that for sufficiently large n and any input x with |x|=n, Space. M(x) = s(n).

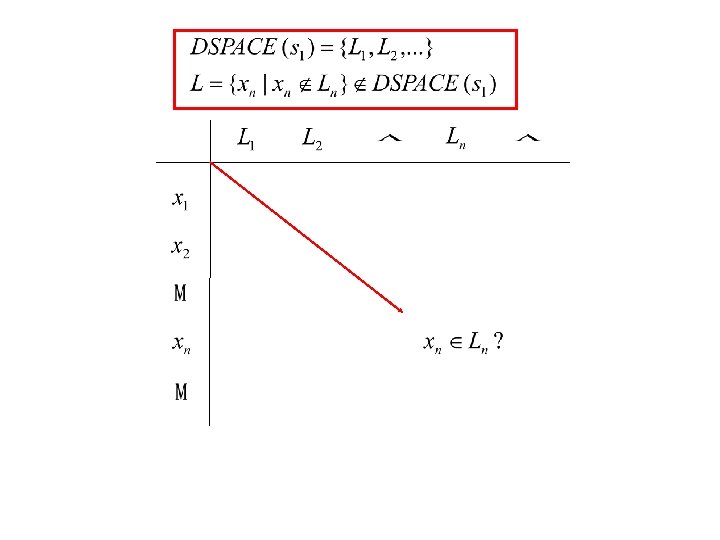
Space Hierarchy If • s 2(n) is a fully space-constructible function, • s 1(n)/s 2(n) → 0 as n → ∞, • s 1(n) > log n, (this may be replaced by s (n)/log n → 0 as n → ∞) then DSPACE(s 2(n)) DSPACE(s 1(n)) ≠ Φ 2

Input tape (read only) Storage tapes Output tape (possibly, write only)

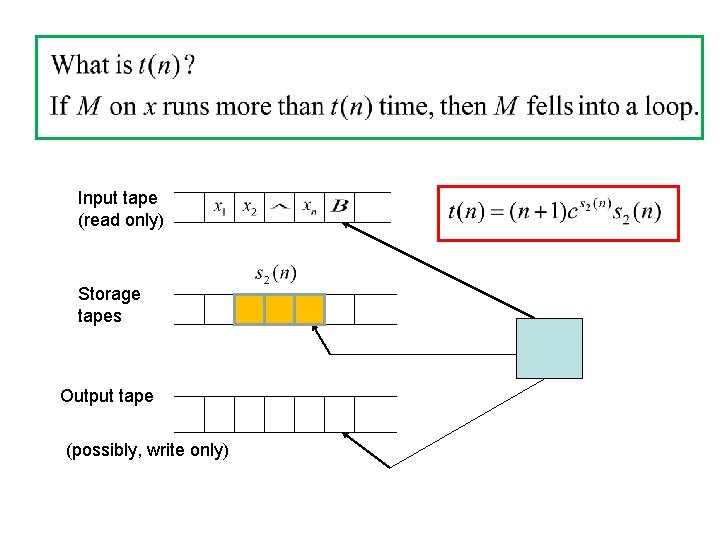
Input tape (read only) Storage tapes Output tape (possibly, write only)

Claim Proof

Claim Proof

Claim Proof

Time Hierarchy

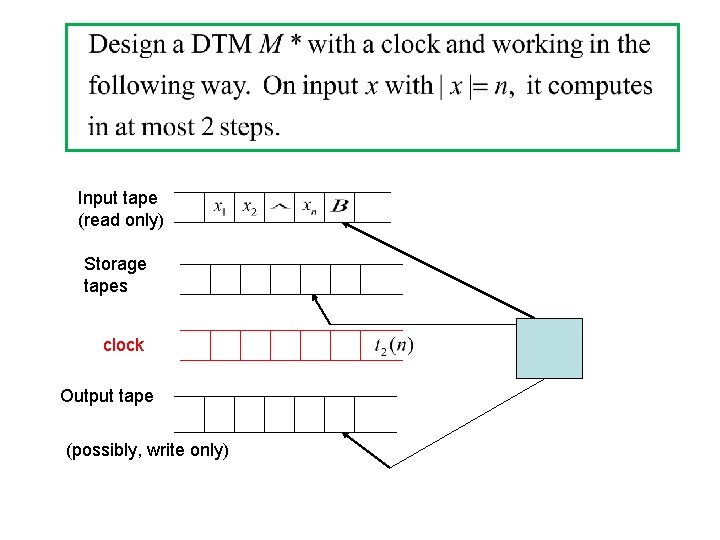
Time-constructible function • t(n) is fully time-constructible if there exists a DTM such that for sufficiently large n and any input x with |x|=n, Time. M(x) = t(n).

Time Hierarchy If • t 1(n) > n+1, • t 2(n) is fully time-constructible, • t 1(n)2 /t 2(n) → 0 as n → infinity, then DTIME(t 2(n)) DTIME(t 1(n)) ≠ Φ

Input tape (read only) Storage tapes clock Output tape (possibly, write only)

Claim Proof ?

Claim Proof

If • t 1(n) > n+1, (this condition may not need) • t 2(n) is fully time-constructible, • t 1(n) log t 1(n) /t 2(n) → 0 as n → infinity, then DTIME(t 2(n)) DTIME(t 1(n)) ≠ Φ

Time Hierarchy If • t 1(n) > n+1, • t 2(n) is fully time-constructible, • t 1(n) log t 1(n) /t 2(n) → 0 as n → infinity, then DTIME(t 2(n)) DTIME(t 1(n)) ≠ Φ

Model Independent Classes c • P = U c>0 DTIME(n ) cn • EXP = U c > 0 DTIME(2 ) n c • EXPOLY = U c > 0 DTIME(2 ) c • PSPACE = U c > 0 DSPACE(n )

PSPACE≠EXP

Problems in P • Are they in P? Sorting minimum spanning tree shortest path maximum flow

Problems in P • None of following is in P? Sorting minimum spanning tree shortest path maximum flow • They are all polynomial-time computable functions

P contains only languages or decision problems • A decision problem is a problem who has only two answers, YES and NO. • A decision problem can be described by a language consisting of all inputs at which YES answer would be obtained.

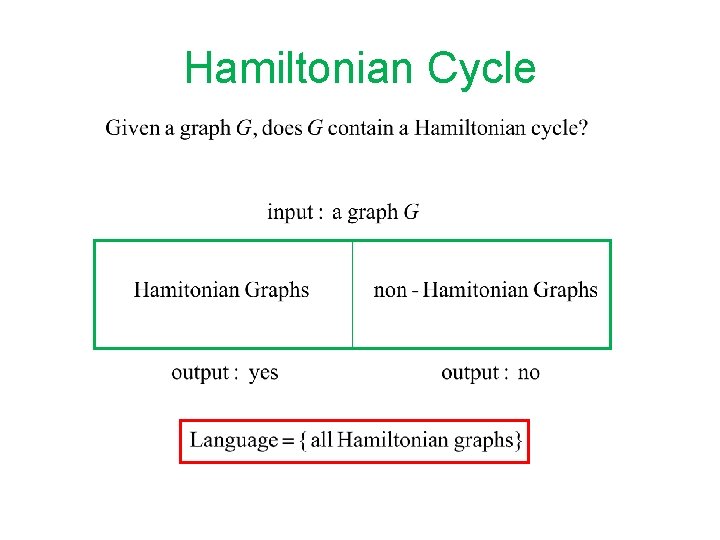
Hamiltonian Cycle

Every optimization problem has a decision version Minimum spanning tree Decision version of minimum spanning tree

For optimization problem with integer value, the decision version is equivalent to it.

Problem in EXP • • • Traveling Salesman Problem Minimum Vertex Cover Hamiltonian Cycle Satisfiability Partition

Edmonds Conjecture in 1965 • Traveling Salesman Problem cannot be solved in polynomial time.