Lecture 06 Analysis II Controllability and Observability 6

Lecture 06 Analysis (II) Controllability and Observability 6. 1 Controllability and Observability 6. 2 Kalman Canonical Decomposition 6. 3 Pole-zero Cancellation in Transfer Function 6. 4 Minimum Realization Modern Contral Systems 1

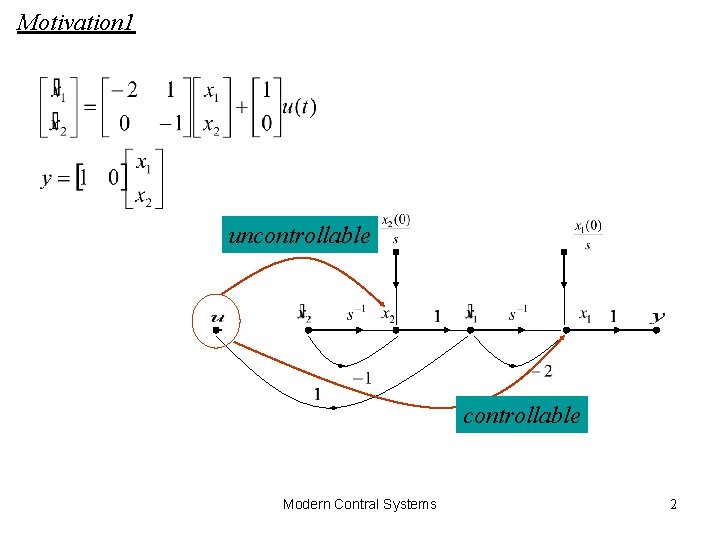
Motivation 1 uncontrollable Modern Contral Systems 2

Controllability and Observability Plant: Definition of Controllability A system is said to be (state) controllable at time , if there exists a finite such for any and any , there exist an input that will transfer the state to the state at time , otherwise the system is said to be uncontrollable at time. Modern Contral Systems 3

Controllability Matrix Example: An Uncontrollable System ※ State is uncontrollable. Modern Contral Systems 4

Proof of controllability matrix Initial condition Modern Contral Systems 5

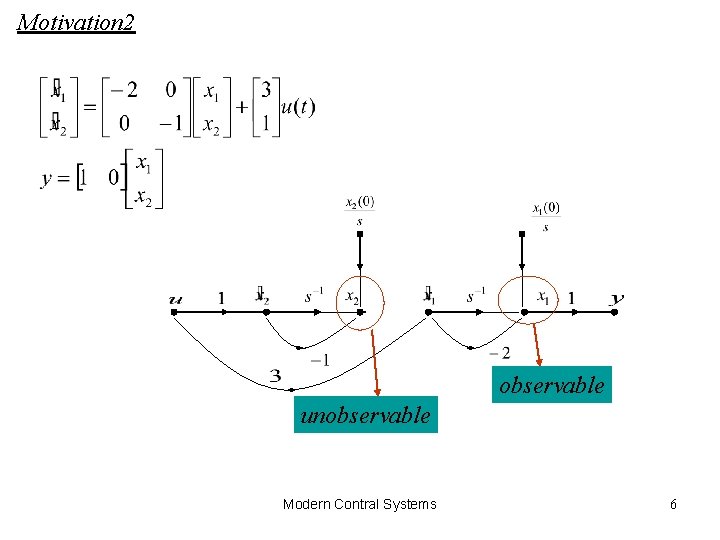
Motivation 2 observable unobservable Modern Contral Systems 6

Definition of Observability A system is said to be (completely state) observable at time , if there exists a finite such that for any at time , the knowledge of the input and the output over the time interval suffices to determine the state , otherwise the system is said to be unobservable at. Modern Contral Systems 7

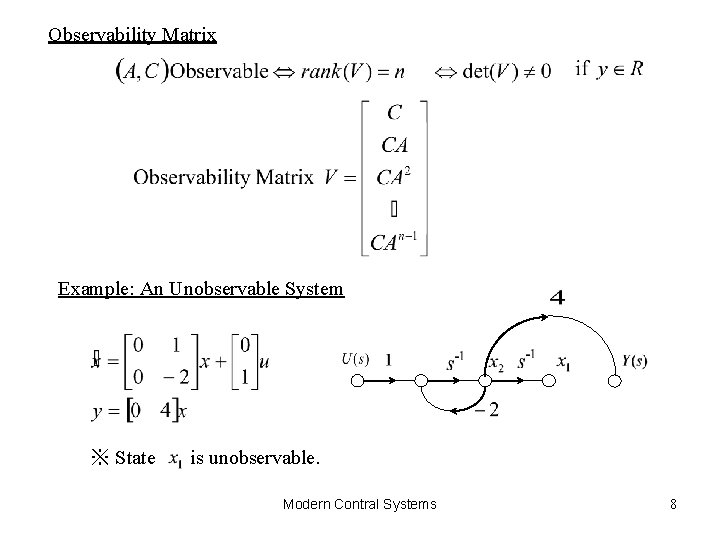
Observability Matrix Example: An Unobservable System ※ State is unobservable. Modern Contral Systems 8

Proof of observability matrix Inputs & outputs Modern Contral Systems 9

Example Plant: Hence the system is both controllable and observable. Modern Contral Systems 10

Theorem I Controllable canonical form Controllable Theorem II Observable canonical form Modern Contral Systems Observable 11

example Controllable canonical form Observable canonical form Modern Contral Systems 12

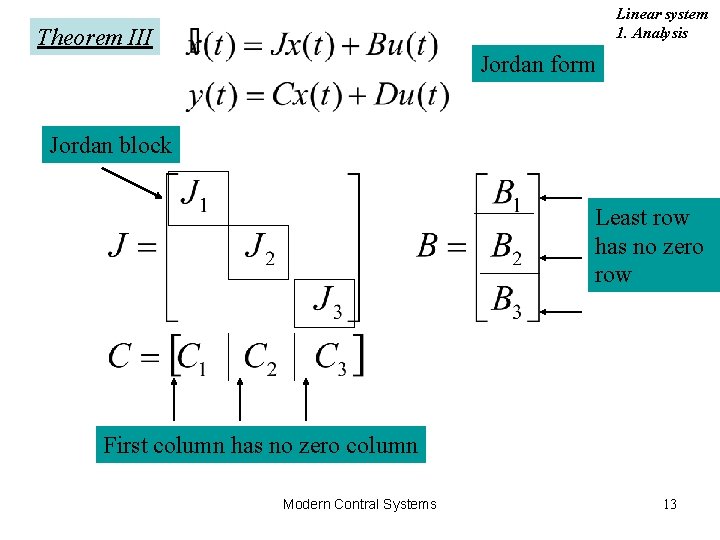
Linear system 1. Analysis Theorem III Jordan form Jordan block Least row has no zero row First column has no zero column Modern Contral Systems 13

Example If uncontrollable If unobservable Modern Contral Systems 14

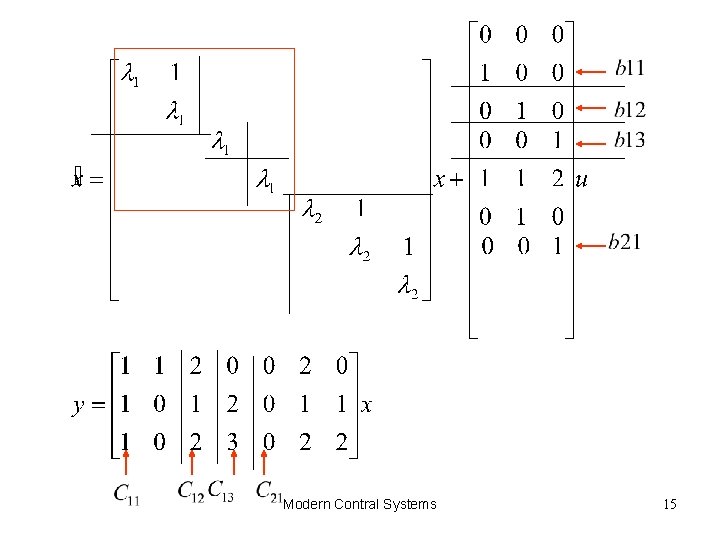
Modern Contral Systems 15

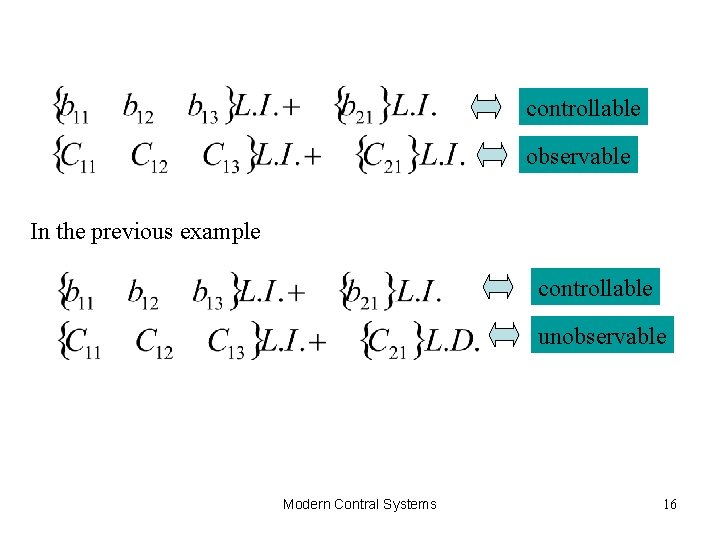
controllable observable In the previous example controllable unobservable Modern Contral Systems 16

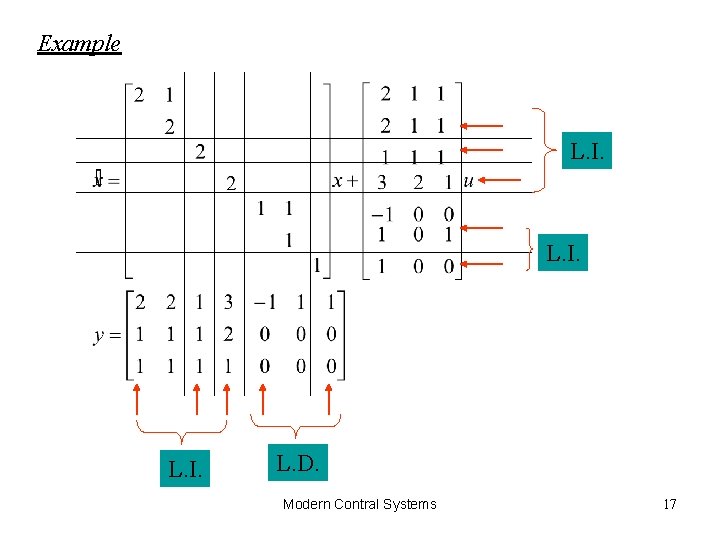
Example L. I. L. D. Modern Contral Systems 17

Kalman Canonical Decomposition Diagonalization: All the Eigenvalues of A are distinct, i. e. There exists a coordinate transform (See Sec. 4. 4) such that System in z-coordinate becomes Homogeneous solution of the above state equation is Modern Contral Systems 18

How to construct coordinate transformation matrix for diagonalization All the Eigenvalues of A are distinct, i. e. The coordinate matrix for diagonalization Consider diagonalized system Modern Contral Systems 19

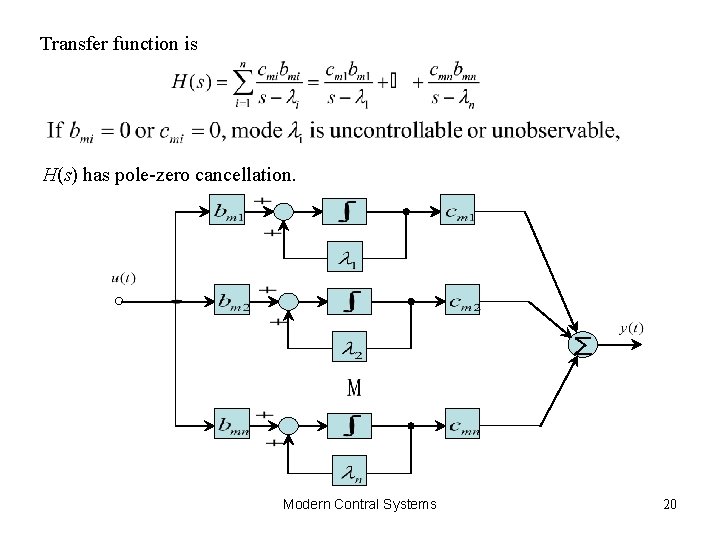
Transfer function is H(s) has pole-zero cancellation. ∑ Modern Contral Systems 20

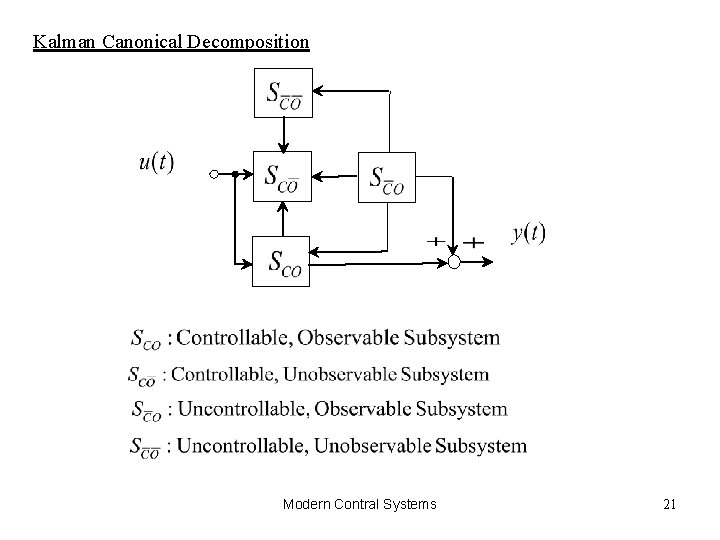
Kalman Canonical Decomposition Modern Contral Systems 21

Kalman Canonical Decomposition: State Space Equation (5. X) Modern Contral Systems 22

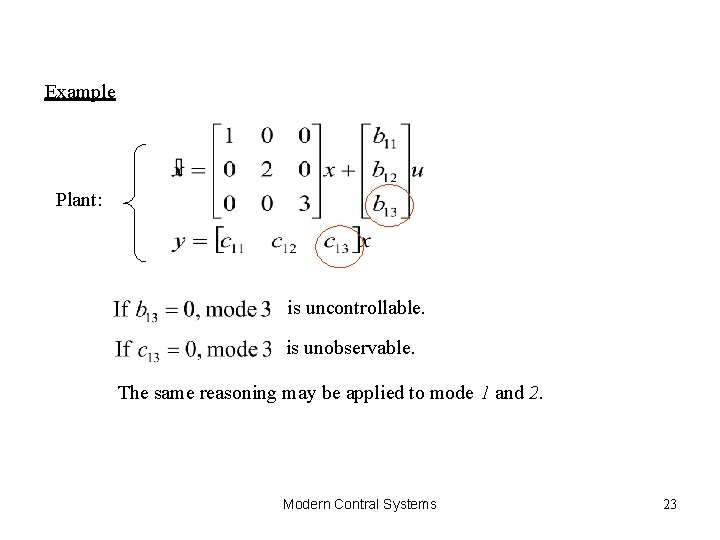
Example Plant: is uncontrollable. is unobservable. The same reasoning may be applied to mode 1 and 2. Modern Contral Systems 23

Pole-zero Cancellation in Transfer Function From Sec. 5. 2, state equation may be transformed to Hence, the T. F. represents the controllable and observable parts of the state variable equation. Modern Contral Systems 24

Example Plant: Transfer Function Modern Contral Systems 25

Example 5. 6 Plant: Transfer Function Modern Contral Systems 26

Minimum Realization: Realize a transfer function via a state space equation. Example Realization of the T. F. Method 1: Method 2: ※There is infinity number of realizations for a given T. F. . Modern Contral Systems 27

Minimum realization: Realize a transfer function via a state space equation with elimination of its uncontrollable and unobservable parts. Example 5. 8 Realization of the T. F. Modern Contral Systems 28