Lecture 04 AC SERIES CIRCUITS VOLTAGE DIVIDER OBJECTIVES

Lecture 04: AC SERIES CIRCUITS, VOLTAGE DIVIDER

OBJECTIVES 1. Relate Ohm’s Law with resistors to Ohm’s Law with impedances. 2. Relate the current phase angle through a component to the voltage phase angle across the component for a resistor, capacitor and inductor. 3. Explain impedance and relate it to resistance and reactance. 4. Explain circuit impedance and circuit phase angle.

OBJECTIVES 5. Compute the total circuit impedance for series RLC circuits. 6. Explain the effects of frequency changes on RLC circuit response. 7. Determine circuit voltages and currents in series RLC circuits. 8. Compute voltage drops across components in an RLC circuit using the voltage divider formula.

Relating Ohm’s Law from DC to AC circuits • Ohm’s still applies even though we have switched from DC to AC circuits. • It just takes on a new form to account for varying frequencies and phase angles.

Relating Ohm’s Law from DC to AC circuits • V=IR becomes V=IZ where Z is the complex impedance.

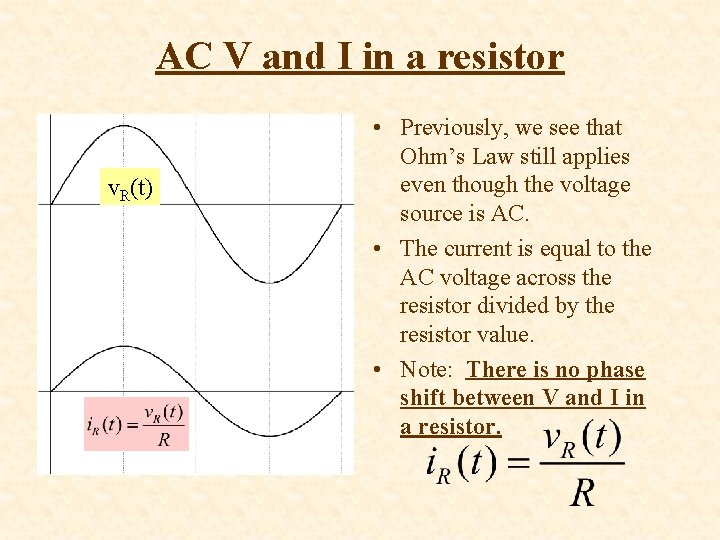
AC V and I in a resistor v. R(t) • Previously, we see that Ohm’s Law still applies even though the voltage source is AC. • The current is equal to the AC voltage across the resistor divided by the resistor value. • Note: There is no phase shift between V and I in a resistor.

AC V and I in a resistor • The magnitude of the current through a resistor is calculated using i= v/R, and from the graph of i and v there was no phase shift from i to v. • We now define the complex impedance of R as:

AC V and I in a resistor • The current through a resistor can be found by writing the voltage as a phasor and dividing by the complex impedance of R. • We see from the final result that the phase shift in a resistor is still 0 o.

AC V and I in a Capacitor • The Capacitive impedance, Zc where =2 f.

AC V and I in a Inductor • We can now define the Inductive impedance, ZL where =2 f.

Impedances Summary Impedance Phasor form: Rectangular form (a + jb) ZR R+j 0 ZL 0+j. XL ZC 0 -j. XC

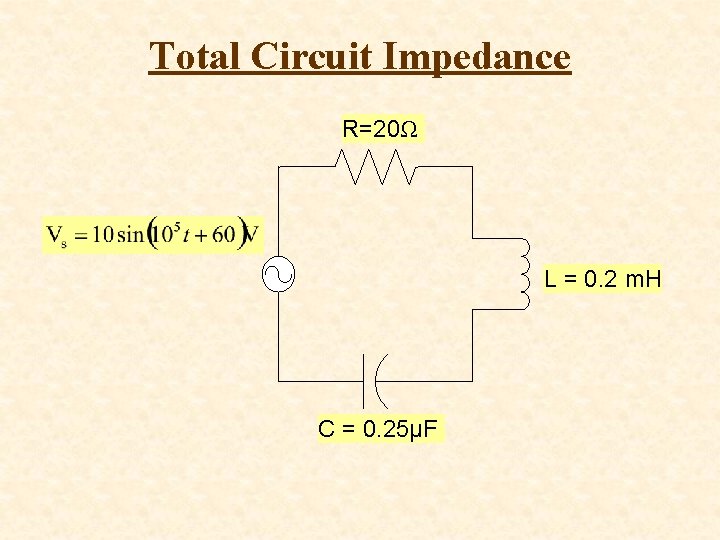
Total Circuit Impedance R=20Ω L = 0. 2 m. H C = 0. 25μF

Total Circuit Impedance

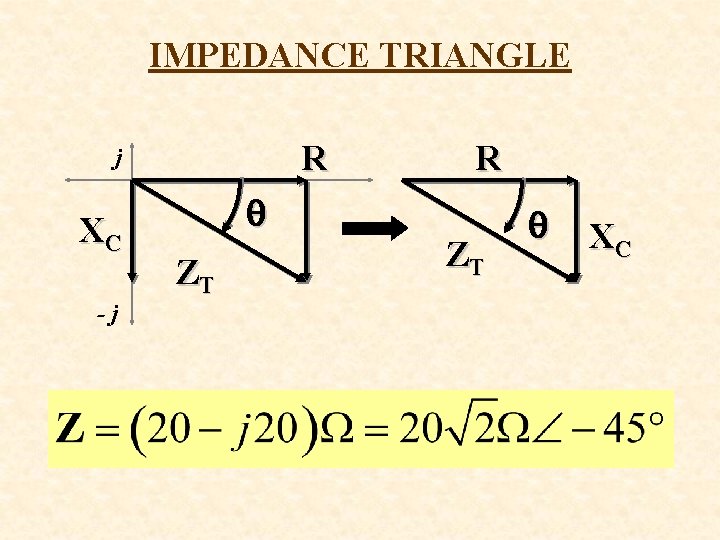
IMPEDANCE TRIANGLE R j XC -j q ZT R ZT q XC

Find is, v. R, v. C, v. L Remember to convert to RMS values when converting from sinusoid to phasors.

Voltage Divider • Voltage divider still works, too.

XL and XC are frequency dependent • Remember that the magnitude of the impedances for Capacitors and Inductors, XC and XL, are frequency dependent. • A new voltage source with a different frequency will cause a different total impedance, thereby changing all of the values in the circuit.