Lecture 02 ITS 033 Programming Algorithms Algorithm Representation

Lecture 02 ITS 033 – Programming & Algorithms Algorithm Representation & Analysis Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 1

Overview n n n Conceptual Flow Pseudo code Asymptotic Notation Growth Rate Common Running Times 2

Lecture 02. 1 ITS 033 – Programming & Algorithms Algorithm Representation: Conceptual Flow Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 3

Conceptual Flow Conceptual flow is a casual diagram showing a flow of thinking process. It can be written using informal diagram (which is not the programming-like Flow Chart. ) Or written in a more formal Pseudo code. 4

Conceptual Flow Example: write a conceptual flow for Nag Screen v Random a number from 0 – 100, if the number is more than 50 then random a location on the screen (25 rows x 80 columns) and print ‘X’, but if the random number is less than or equal to 50 then random a location on the screen and print ‘O’. v Repeat the first step until the screen is fully covered by letters. 5

See example 6

Heuristics is an loosely defined algorithm which is likely to perform faster or better. However, the output is not guaranteed. For example, in Nag Screen Problem, we random the position only 4000 times before we stop. More of Heuristic in Approximation algorithm and AI course in 3 rd year. 7

Problem 1: New world puzzle - revisited n n n n There are N people who want to cross a bridge; they all begin on the same side. It is night, and they have one flashlight. A maximum of two people can cross the bridge at one time and have to have the flashlight with them. Mr. A 1 takes T 1 minutes to cross the bridge, Mr. A 2 takes T 2 minutes to cross the bridge, Mr. A 3 takes T 3 minutes to cross the bridge, Mr. An takes Tn minutes to cross the bridge, ¨ T 1 < T 2 < T 3 < T 4 < … < T n A pair must walk together at the rate of the slower person’s pace. For example, Mr. A 2 and Mr. A 8 have to take T 8 minutes to get across the bridge. Design an Algorithm to move them all to the other side of the bridge with minimum total time. 8

See example 9

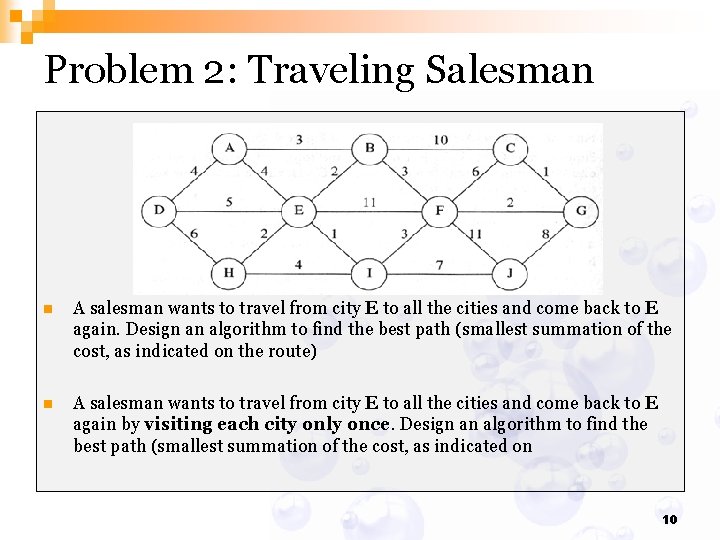
Problem 2: Traveling Salesman n A salesman wants to travel from city E to all the cities and come back to E again. Design an algorithm to find the best path (smallest summation of the cost, as indicated on the route) n A salesman wants to travel from city E to all the cities and come back to E again by visiting each city only once. Design an algorithm to find the best path (smallest summation of the cost, as indicated on 10

See example 11

Conceptual Flow Weakness Conceptual flow is probably too casual and can sometime only be understood by the person who created it. For communication and analysis purposes, a more formal Pseudo code may be used instead. 12

Lecture 02. 2 ITS 033 – Programming & Algorithms Algorithm Representation: Psudo Code Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 13

Pseudo code n n n High-level description of an algorithm More structured than English paragraph Less detailed than a program Preferred notation for describing algorithms Hides program design issues 14

Example of Pseudo code Algorithm array. Max 1(A, n) Input array A of n integers Output maximum element of A for i 1 to n 1 do max true; for r i+1 to n do if A[i] < A[r] then max false exit; if (max = true) return (A[i]); 15

Pseudo code n Algorithm header Algorithm method (arg [, arg…]) Input … Output … n Control flow ¨ if … then … [else …] ¨ while … do … ¨ repeat … until … ¨ for … do … ¨ Indentation replaces braces 16

Pseudo code n Method call var. method (arg [, arg…]) n Return value return expression n Expressions Assignment = Equality testing n 2 Superscripts and other mathematical formatting allowed 17

Pseudo code A structure of an algorithm using Pseudo code Algorithm what is the name of your algorithm ? Input What is your input for this ? Output what will you get after process the input ? the algorithm itself. 18

Pseudo code Design an algorithm with Pseudo code to find a maximum value in an array with n elements. ? 19

Algorithm array. Max 2(A, n) This algorithm is better than the previous one Algorithm array. Max 2(A, n) Input array A of n integers Output maximum element of A current. Max A[0] for i 1 to n 1 do if A[i] current. Max then current. Max A[i] set current. Max to A[0] repeat n-1 times starting from i = 1 return current. Max if element no. i current. Max then set current. Max to this element 20

Example of Pseudo code Algorithm array. Max 1(A, n) Input array A of n integers Output maximum element of A for i 1 to n 1 do max true; for r i+1 to n do if A[i] < A[r] then max false exit; if (max = true) return (A[i]); Algorithm array. Max 1(A, n) Input array A of n integers Output maximum element of A repeat n-1 times starting from i – 1 assume that element no. i is a max repeat starting from r = i+1 until r=n if element no. i < element no. r then element no. i is not a max if (max = true) return (A[i]); 21

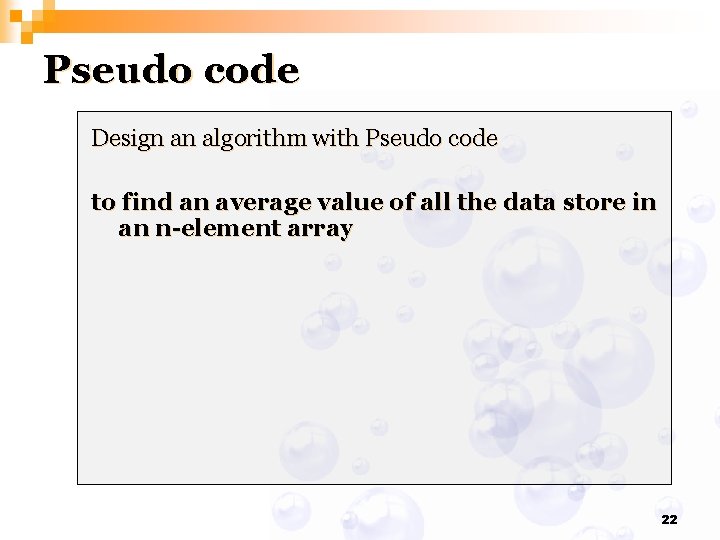
Pseudo code Design an algorithm with Pseudo code to find an average value of all the data store in an n-element array 22

ITS 033 – Programming & Algorithms Lecture 02. 3 Algorithm Complexity Analysis Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 23

Complexity Analysis: How can we measure the efficiency of an algorithm ? the fundamental importance to the design of efficient algorithm is its “Running Time”. After all, time is the most precious measure of an algorithm’s efficiency. 24

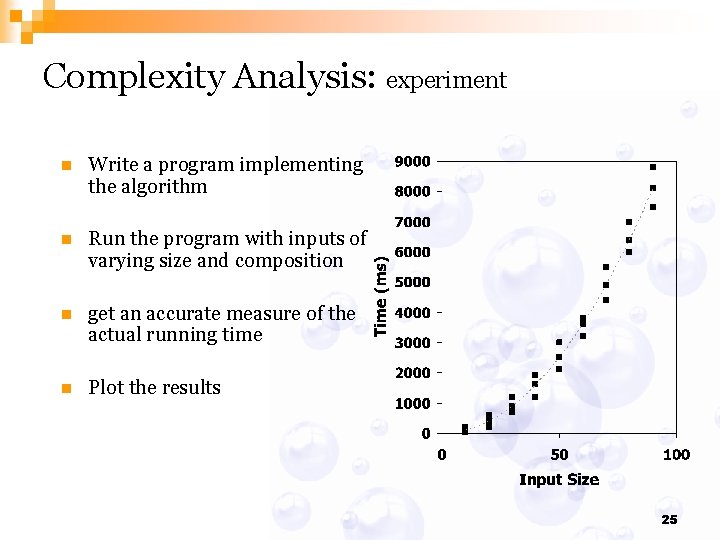
Complexity Analysis: experiment n Write a program implementing the algorithm n Run the program with inputs of varying size and composition n get an accurate measure of the actual running time n Plot the results 25

Complexity Analysis: Limitations of Experiments n It is necessary to implement the algorithm, which may be difficult n Results may not be indicative of the running time on other inputs not included in the experiment. n In order to compare two algorithms, the same hardware and software environments must be used 26

Complexity Analysis: Theoretical Analysis n Uses a high-level description of the algorithm instead of an implementation n Characterizes running time as a function of the input size, n. n Takes into account all possible inputs n Allows us to evaluate the speed of an algorithm independent of the hardware/software environment 27

Complexity Analysis: bound The bound of the running time could be estimated by computing the number of times which the basic operation is executed 28

Basic Operation ‘Basic Operations’ are the most important operation of the algorithm or the operation contributing the most to the total running time. Normally, it is not difficult to identify the basic operation of an algorithm. It is usually the most time-consuming operation in the algorithm’s inner-most loop. 29

Basic Operations n Basic computations performed by an algorithm n Identifiable in pseudocode n Largely independent from the programming language n Exact definition not important (we will see why later) n Assumed to take a constant amount of time 30

Bound is a function of input size, N n By inspecting the pseudocode, we can determine the maximum number of basic operations executed by an algorithm, as a function of the input size, n 31

Example n For each of the following algorithms, indicate A natural size for its input ¨ Its basic operation ¨ 1. 2. 3. Computing the sum of n numbers Computing n! Finding the largest element in a list of n numbers 32

Example n Consider the algorithm for adding two n-by-n matrices. What is its basic operation? ¨ How many times is it performed as a function of the matrix order n? ¨ How many times is it performed as a function of the total number of element, N? ¨ 33

Counting Basic Operations Student A’s counting Algorithm array. Max(A, n) current. Max A[0] for i 1 to n 1 do if A[i] current. Max then current. Max A[i] return current. Max number of operations for this line 2 n-1 2(n 1) 1 Total 5 n - 1 Student B’s counting Algorithm array. Max(A, n) current. Max A[0] for i 1 to n 1 do if A[i] current. Max then current. Max A[i] return current. Max number of operations for this line 2 2+ n 2(n 1) 1 Total 5 n + 1 34

Extra example 35

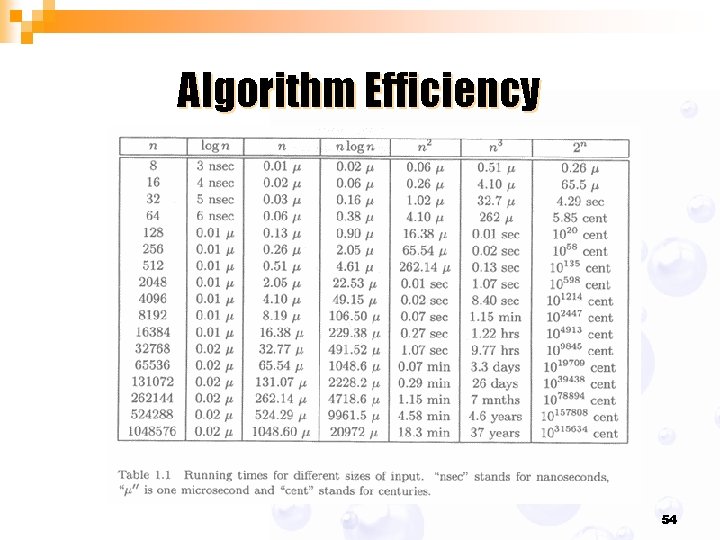
Algorithm Efficiency 36

ITS 033 – Programming & Algorithms Lecture 02. 4 Order of Growth Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 37

Growth Rate of Running Time n Changing the hardware/ software environment ¨ Affects T(n) by a constant factor, but ¨ Does not alter the growth rate of T(n) n The linear growth rate of the running time T(n) is an intrinsic property of algorithm array. Max 38

Big-Oh Notation Formal Definition n Given functions f(n) and g(n), we say that f(n) is O(g(n)) if there are positive constants c and n 0 such that f(n) cg(n) for all n n 0 Informal definition Big Oh is a function which is an upper bound of a function in question. It indicates the class of performance of that algorithm. It’s like putting a bicycle and a car into a race. The are in different classes. 39

Algorithm Efficiency 40

More Big-Oh Examples 7 n-2 is O(n) need c > 0 and n 0 1 such that 7 n-2 c • n for n n 0 this is true for c = 7 and n 0 = 1 n 3 n 3 + 20 n 2 + 5 is O(n 3) need c > 0 and n 0 1 such that 3 n 3 + 20 n 2 + 5 c • n 3 for n n 0 this is true for c = 4 and n 0 = 21 n 3 log n + log log n is O(log n) need c > 0 and n 0 1 such that 3 log n + log n c • log n for n n 0 this is true for c = 4 and n 0 = 2 41

Big-Oh Rules n If is f(n) a polynomial of degree d, then f(n) is O(nd), i. e. , 1. Drop lower-order terms 2. Drop constant factors n Use the smallest possible class of functions ¨ Say “ 2 n is O(n)” instead of “ 2 n is O(n 2)” n Use the simplest expression of the class ¨ Say “ 3 n + 5 is O(n)” instead of “ 3 n + 5 is O(3 n)” 42

More Big-Oh Examples what are Big-O for these functions ? 7 n-2 3 n 3 + 20 n 2 + 5 21, 207 n – 211 n 4 + 23 n 4 – 20 n 3 + 2 n – 211 3 log n + log n 43

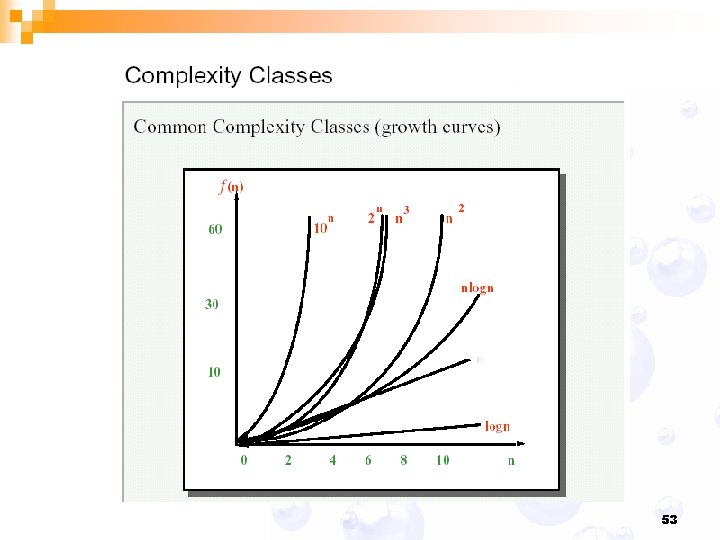
Big-Oh and Growth Rate n The big-Oh notation gives an upper bound on the growth rate of a function n The statement “f(n) is O(g(n))” means that the growth rate of f(n) is no more than the growth rate of g(n) n We can use the big-Oh notation to rank functions according to their growth rate from best to worst n O(1) O(log n) O(n 2) O(n 3) O(2 n) O(n!) n n n n 44

Lecture 02. 5 ITS 033 – Programming & Algorithms Common Running Times Asst. Prof. Dr. Bunyarit Uyyanonvara IT Program, Image and Vision Computing Lab. School of Information, Computer and Communication Technology (ICT) Sirindhorn International Institute of Technology (SIIT) Thammasat University http: //www. siit. tu. ac. th/bunyarit@siit. tu. ac. th 02 5013505 X 2005 45

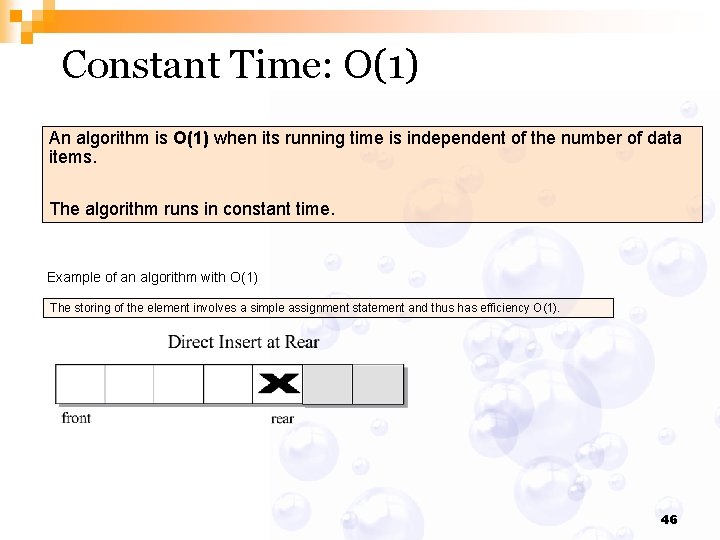
Constant Time: O(1) An algorithm is O(1) when its running time is independent of the number of data items. The algorithm runs in constant time. Example of an algorithm with O(1) The storing of the element involves a simple assignment statement and thus has efficiency O(1). 46

Logarithmic Time : O(log n) An algorithm is O(log n) is among the best algorithms. Typically a result of cutting a problem’s size by a constant factor on each iteration of the algorithm. When the number of elements doubles, the number of operations increases by just 1. 47

Linear Time Algorithms: O(n) An algorithm is O(n) when its running time is proportional to the size of the list. When the number of elements doubles, the number of operations doubles. 48

n-log-n Algorithms: O(n log n) An algorithm is O(n log n) are from many divide-and-conquer algorithms. A little bit slower than O(n) but it is still consider very good algorithm. 49

Quadractic & Cubic : O(n 2) n Algorithms with running time O(n 2) are quadratic. ¨ practical only for relatively small values of n. n Whenever n doubles, the running time of the algorithm increases by a factor of 4. n Algorithms with running time O(n 3)are cubic. ¨ efficiency is generally poor; doubling the size of n increases the running time eight-fold. 50

Exponential : O(2 n) Typical for algorithms that generate all subsets of an n-element set. Often the term exponential is used in a broader sense to include this and larger orders of growth as well. Considered as bad algorithm. 51

Factorial Time : O(n!) Typical for algorithms that generate all permutations fo an n-element set. Considered as worst algorithm. O(n!), sometimes, reads Oh! No! Algorithm. 52

53

Algorithm Efficiency 54

End of Chapter 2 Thank You! 55