Lecture 02 CS 001 CALCULUS AND ANALYTIC GEOMETRY

Lecture 02 CS 001 CALCULUS AND ANALYTIC GEOMETRY

Rectangular Coordinate Systems • We shall now show to assign an ordered pair (a, b) of real numbers to each point in a plane. Although we have also used the notation (a, b) to denote an open interval, there is little chance for confusion, since it should always be clear from our discussion whether (a, b) represents a point or an interval. 2

Rectangular Coordinate Systems • We introduce a rectangular, or Cartesian, coordinate system in a plane by means of two perpendicular coordinate lines, called coordinate axes, that intersect at the origin O, as shown in Figure 1. Figure 3

Rectangular Coordinate Systems • We often refer to the horizontal line as the x-axis and the vertical line as the y-axis and label them x and y, respectively. The plane is then a coordinate plane, or an xy-plane. The coordinate axes divide the plane into four parts called the first, second, third, and fourth quadrants, labeled I, III, and IV, respectively (see Figure 1). Points on the axes do not belong to any quadrant. Each point P in an xy-plane may be assigned an ordered pair (a, b), as shown in Figure 1. 4

Rectangular Coordinate Systems • We call a the x-coordinate (or abscissa) of P, and b the y-coordinate (or ordinate). We say that P has coordinates (a, b) and refer to the point (a, b) or the point P (a, b). • Conversely, every orderedpair (a, b) determines a point P with coordinates a and b. We plot a point by using a dot, as illustrated in Figure 2. Figure 5

Rectangular Coordinate Systems • Distance between two points • The length of a horizontal line segment is the abscissa (x coordinate) of the point on the right minus the abscissa (x coordinate) of the point on the left. Distance D = X 2 – X 1 Distance d= x 2 – x 1 6

Rectangular Coordinate Systems • Distance between two points • The length of a vertical line segment is the ordinate (y coordinate) of the upper point minus the ordinate (y coordinate) of the lower point. • Distance D = y 2 – y 1 7

Rectangular Coordinate Systems • To determine the distance between two points of a slant line segment add the square of the difference of the abscissa to the square of the difference of the ordinates and take the positive square root of the sum. 8

Rectangular Coordinate Systems • 9

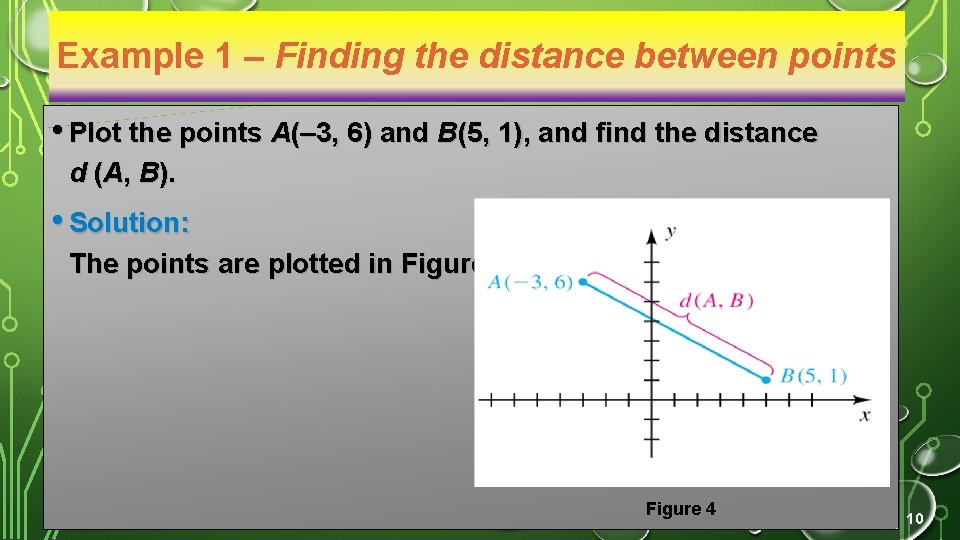
Example 1 – Finding the distance between points • Plot the points A(– 3, 6) and B(5, 1), and find the distance d (A, B). • Solution: The points are plotted in Figure 4 10

• By the distance formula, • d (A , B ) = • = • • = = • 9. 43. 11

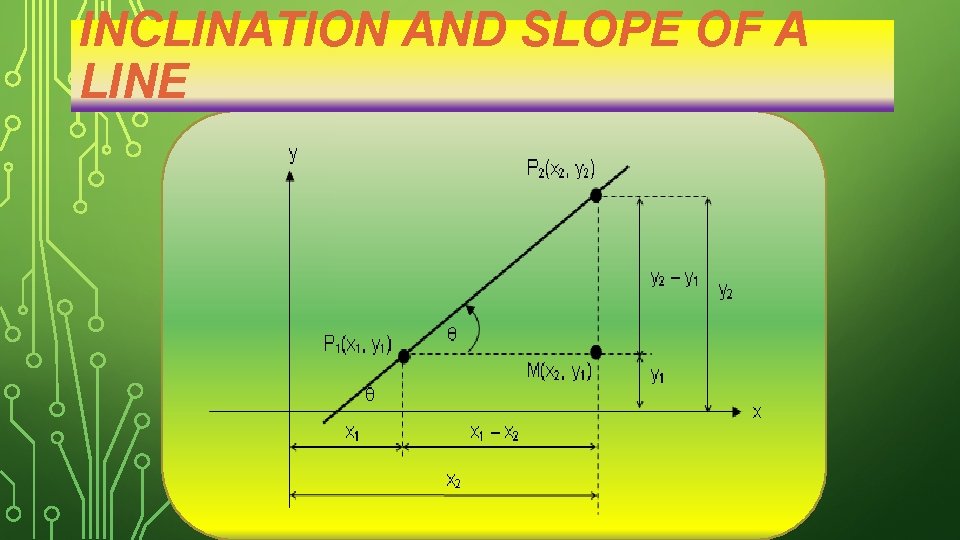
INCLINATION AND SLOPE OF A LINE The inclination of the line, L, (not parallel to the x-axis) is defined as the smallest positive angle measured from the positive direction of the x-axis or the counterclockwise direction to L. The slope of the line is defined as the tangent of the angle of inclination. 12

INCLINATION AND SLOPE OF A LINE

INCLINATION AND SLOPE OF A LINE

PARALLEL AND PERPENDICULAR LINES If two lines are parallel their slope are equal (m 1= m 2). If two lines are perpendicular the slope of one of the line is the negative reciprocal of the slope of the other line. If m 1 is the slope of L 1 and m 2 is the slope of L 2 then, or m 1 m 2 = -1. 15

16

17

18

MIDPOINT OF A LINE • 19

20

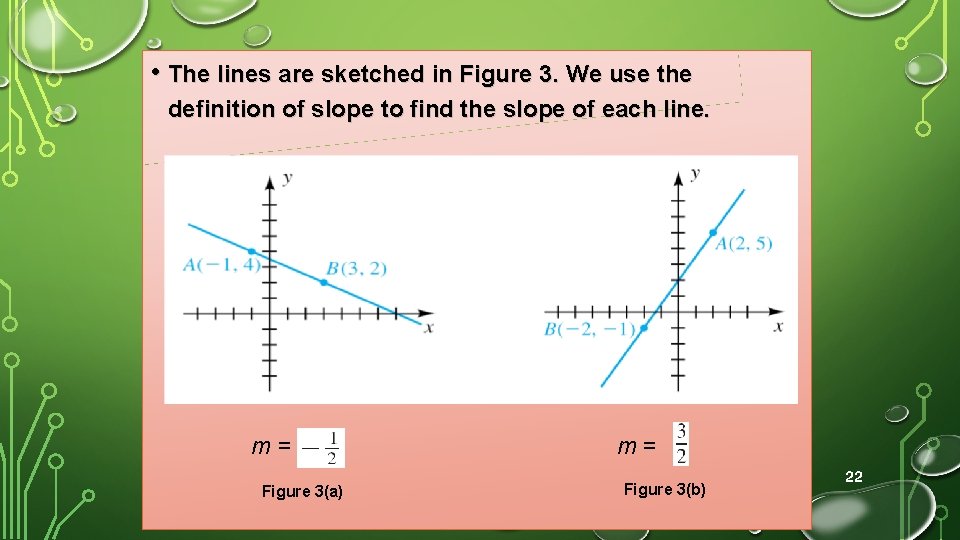
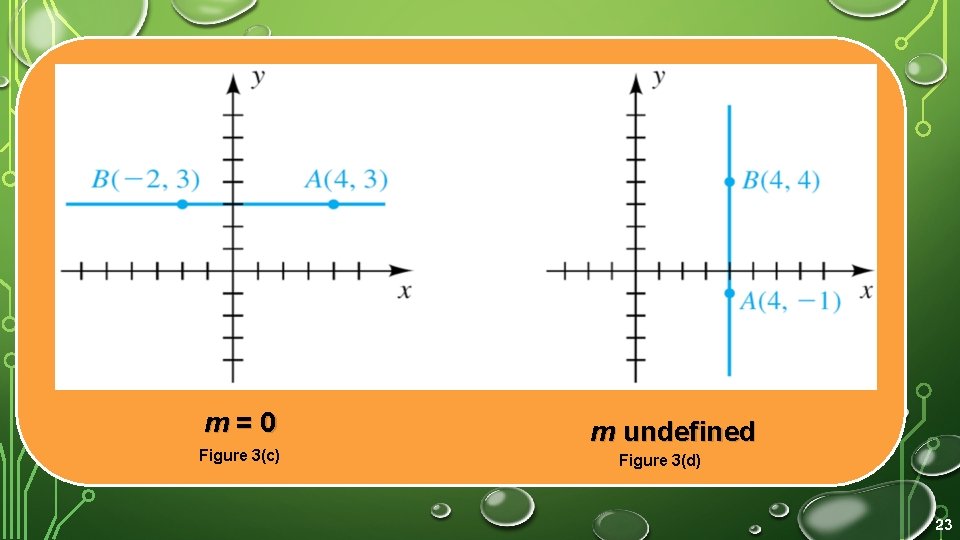
Example 1 – Finding slopes • Sketch the line through each pair of points, and find its slope m: • (a) A(– 1, 4) and B(3, 2) • (b) A(2, 5) and B(– 2, – 1) • (c) A(4, 3) and B(– 2, 3) • (d) A(4, – 1) and B(4, 4) 21

• The lines are sketched in Figure 3. We use the definition of slope to find the slope of each line. m= Figure 3(a) m= Figure 3(b) 22

m=0 Figure 3(c) m undefined Figure 3(d) 23

• (a) • (b) • (c) • (d) The slope is undefined because the line is parallel to the y-axis. Note that if the formula for m is used, the denominator is zero. 24

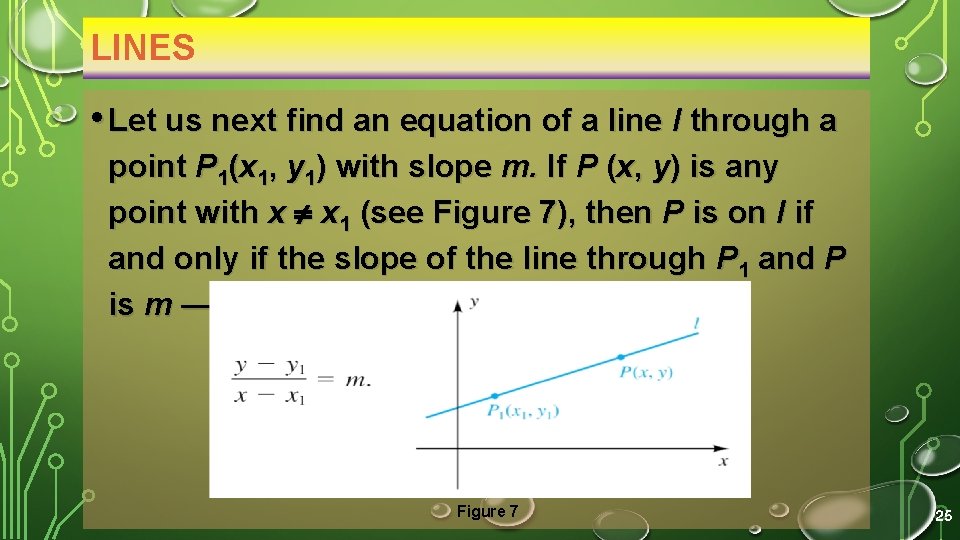
LINES • Let us next find an equation of a line l through a point P 1(x 1, y 1) with slope m. If P (x, y) is any point with x x 1 (see Figure 7), then P is on l if and only if the slope of the line through P 1 and P is m — that is, if Figure 7 25

LINES • This equation may be written in the form • y – y 1 = m(x – x 1). • Note that (x 1, y 1) is a solution of the last equation, and hence the points on l are precisely the points that correspond to the solutions. • This equation for l is referred to as the point- 26

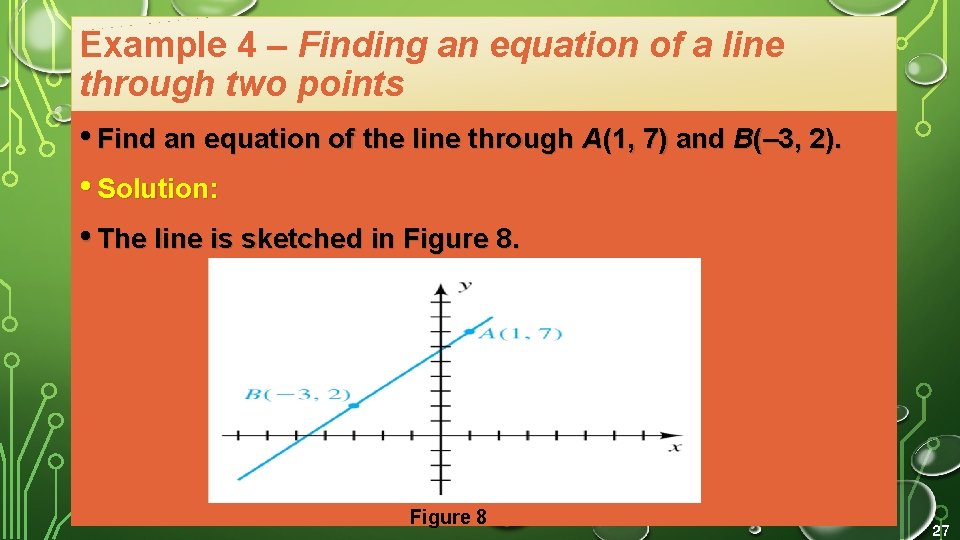
Example 4 – Finding an equation of a line through two points • Find an equation of the line through A(1, 7) and B(– 3, 2). • Solution: • The line is sketched in Figure 8 27

• The formula for the slope m gives us • We may use the coordinates of either A or B for (x 1, y 1) in the point-slope form. 28

• Using A(1, 7) gives us the following: • • y– 7= (x – 1) 4(y – 7) = 5(x – 1) 29

• 4 y – 28 = 5 x – 5 • – 5 x + 4 y = 23 • 5 x – 4 y = – 23 • The last equation is one of the desired forms for an equation of a line. • Another is 5 x – 4 y + 23 = 0. 30

EXAMPLE 31

EXAMPLE 32

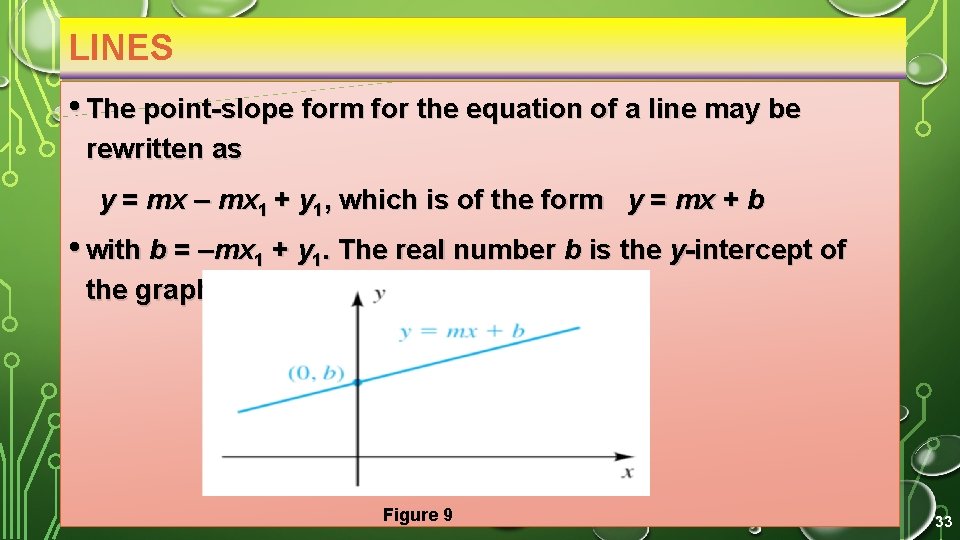
LINES • The point-slope form for the equation of a line may be rewritten as y = mx – mx 1 + y 1, which is of the form y = mx + b • with b = –mx 1 + y 1. The real number b is the y-intercept of the graph, as indicated in Figure 9 33

Example 5 – Expressing an equation in slopeintercept form • Express the equation 2 x – 5 y = 8 in slope-intercept form. • Solution: • Our goal is to solve the given equation for y to obtain the form • • • y = mx + b. We may proceed as follows: given 2 x – 5 y = 8 34

• – 5 y = – 2 x + 8 • y= subtract 2 x divide by – 5 equivalent equation • The last equation is the slope-intercept form y = mx + b with slope • m= and y-intercept b = . 35

TRY THIS Find distance from A to B , write an equation for the line through A and B and find a midpoint in problem 1 -4. Write line equation in problem 19 - 21 36

TRY THIS 37