Lect 13 Public Key Encryption RSA El Gamal

Lect. 13 : Public Key Encryption RSA El. Gamal 1

RSA Public Key Systems v RSA is the first public key cryptosystem v Proposed in 1977 by Ron Rivest, Adi Shamir and Leonard Adleman at MIT v It is believed to be secure and still widely used Shamir Rivest Adleman 2

RSA Public Key Systems v Key generation Ø Choose two large (512 bits or more) primes p & q Ø Compute modulus n = pq, and (n) = (p-1)(q-1) Ø Pick an integer e relatively prime to (n), gcd(e, (n))=1 Ø Compute d such that ed = 1 mod (n) Ø Public key (n, e) : publish Ø Private key d : keep secret (may discard p & q) v Special Property Ø (me mod n)d mod n = (md mod n)e mod n for 0 < m < n v Encryption / Decryption Ø E: c = me mod n for 0 < m < n Ø D: m = cd mod n Ø Proof) Cd = (Me)d = Med = Mk (n) +1 = M {M (n)}k = M 3

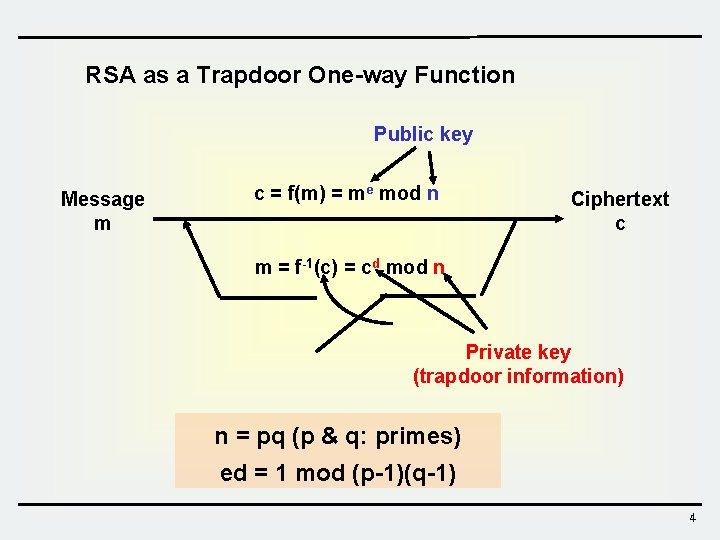
RSA as a Trapdoor One-way Function Public key Message m c = f(m) = me mod n Ciphertext c m = f-1(c) = cd mod n Private key (trapdoor information) n = pq (p & q: primes) ed = 1 mod (p-1)(q-1) 4

RSA Public Key Systems v Example: Key Generation – – – p=3, q=11 n = pq = 33, (n) =(p-1)(q-1) = 2 x 10 = 20 e = 3 s. t. gcd(e, (n) )=(3, 20)=1 Choose d s. t. ed =1 mod (n), 3 d = 1 mod 20, d=7 Public key ={e, n}={3, 33}, private key ={d}={7} Encryption – M =5 – C = Me mod n = 53 mod 33 =26 Decryption – M =Cd mod n = 267 mod 33= 5 5

RSA Public Key Systems Ø Exercise 3: Provide an example of RSA key generation, encryption, and decryption for 1) p=17, q=23 (by hand calculation) 2) p=2357, q=2551 (using big number calculator) 3) p=885320963, q=238855417 (using big number calculator) 1. Key generation 2. Encryption 3. Decryption 6

Selecting Primes p and q for RSA v How to select primes p and q ? 1. |p| |q| to avoid ECM (Elliptic Curve Method for factoring) 2. p-q must be large to avoid trial division 3. p and q are strong prime § p-1 has large prime factor r (pollard’s p-1) § p+1 has large prime factor (William’s p+1) § r-1 has large prime factor (cyclic attack) 7

Security of RSA v Common Modulus attack: v If multiple entities share the same modulus n=pq with different pairs of (ei, di), it is not secure. Do not share the same modulus! v Cryptanalysis: If the same message M was encrypted to different users User u 1 : C 1 = Me 1 mod n User u 2 : C 2 = Me 2 mod n If gcd(e 1, e 2)=1, there a and b s. t. ae 1 + be 2 = 1 mod n Then, (C 1)a(C 2)b mod n = (Me 1)a(Me 2)b mod n = Mae 1+be 2 mod n = M mod n 8

Security of RSA v Cycling attack If f(f( …f(M)))=f(M) where f(M) = Me mod n ? If a given ciphertext appears after some iterations, we can recover the plaintext at collusion point. Let C=Me mod n If (((Ce)e)…)e mod n = Ce^k mod n = C, then Ce^(k-1) mod n = M v Multiplicative attack (homomorphic property of RSA) (M 1 e) (M 2 e) mod n = (M 1 x M 2 ) e mod n 9

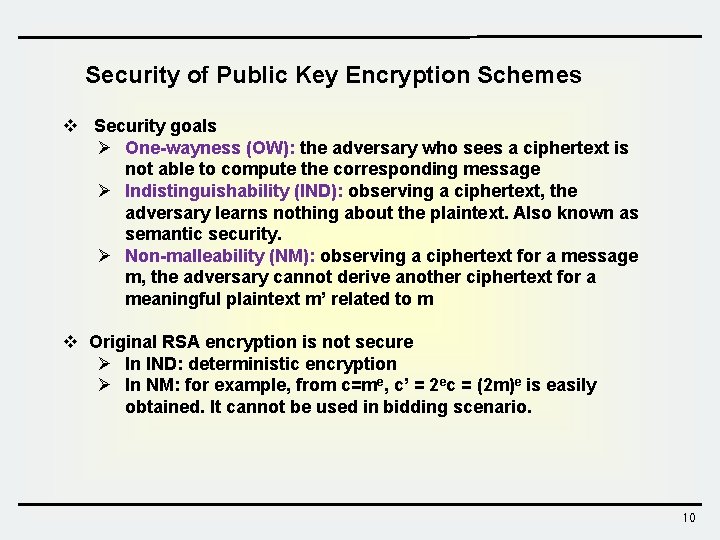
Security of Public Key Encryption Schemes v Security goals Ø One-wayness (OW): the adversary who sees a ciphertext is not able to compute the corresponding message Ø Indistinguishability (IND): observing a ciphertext, the adversary learns nothing about the plaintext. Also known as semantic security. Ø Non-malleability (NM): observing a ciphertext for a message m, the adversary cannot derive another ciphertext for a meaningful plaintext m’ related to m v Original RSA encryption is not secure Ø In IND: deterministic encryption Ø In NM: for example, from c=me, c’ = 2 ec = (2 m)e is easily obtained. It cannot be used in bidding scenario. 10

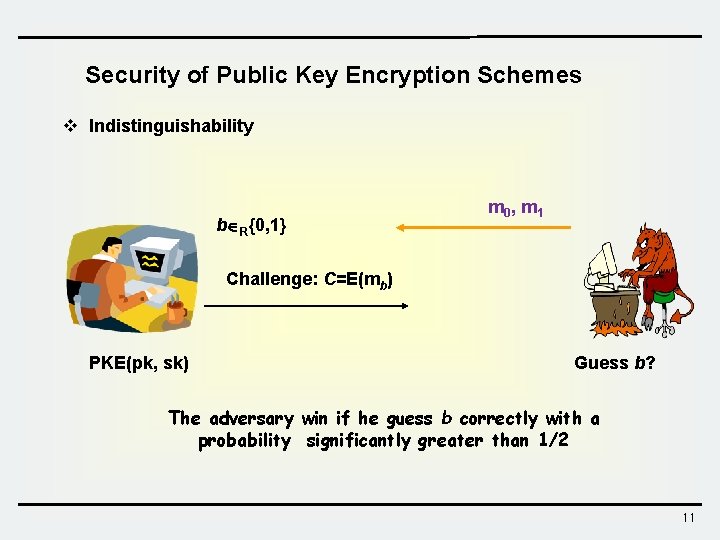
Security of Public Key Encryption Schemes v Indistinguishability b R{0, 1} m 0 , m 1 Challenge: C=E(mb) PKE(pk, sk) Guess b? The adversary win if he guess b correctly with a probability significantly greater than 1/2 11

Security of Public Key Encryption Schemes v Assume the existence of Decryption Oracle v Mimics an attacker’s access to the decryption device v Attack models Ø Chosen Plaintext Attack (CPA): the adversary can encrypt any plaintext of his choice. In public key encryption this is always possible. Ø Non-adaptive Chosen Ciphertext Attack (CCA 1): the attacker has access to the decryption oracle before he sees a ciphertext that he wishes to manipulate (lunchtime attack) Ø Adaptive Chosen Ciphertext Attack (CCA 2): the attacker has access to the decryption oracle before and after he sees a ciphertext c that he wishes to manipulate (but, he is not allowed to query the oracle about the target ciphertext c. ) 12

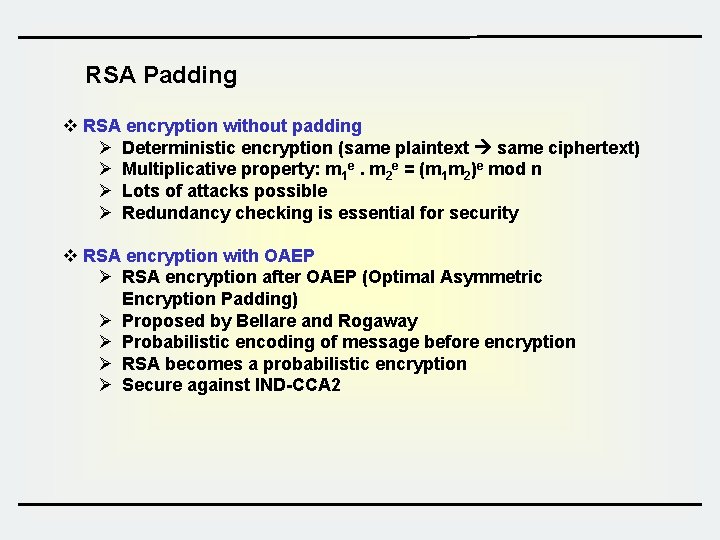
RSA Padding v RSA encryption without padding Ø Deterministic encryption (same plaintext same ciphertext) Ø Multiplicative property: m 1 e. m 2 e = (m 1 m 2)e mod n Ø Lots of attacks possible Ø Redundancy checking is essential for security v RSA encryption with OAEP Ø RSA encryption after OAEP (Optimal Asymmetric Encryption Padding) Ø Proposed by Bellare and Rogaway Ø Probabilistic encoding of message before encryption Ø RSA becomes a probabilistic encryption Ø Secure against IND-CCA 2

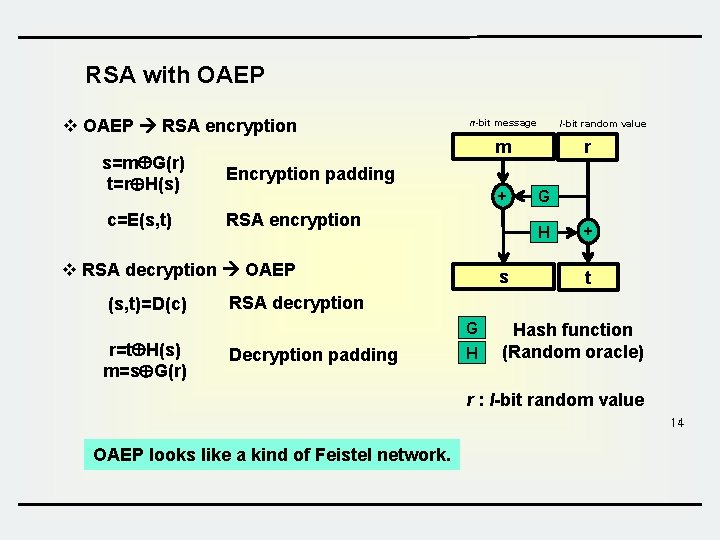
RSA with OAEP v OAEP RSA encryption n-bit message m s=m G(r) t=r H(s) Encryption padding c=E(s, t) RSA encryption + s G + t RSA decryption G r=t H(s) m=s G(r) r H v RSA decryption OAEP (s, t)=D(c) l-bit random value Decryption padding H Hash function (Random oracle) r : l-bit random value 14 OAEP looks like a kind of Feistel network.

RSA Encryption with RSA-OAEP Padding In PKCS #1 v 2. 0, v 2. 1 · Parameter : Hash, MGF · Input : M, L, (n, e) L Seed PS 01 MGF EM = M Hash DB = l. Hash Random string, seed. Len = h. Len MGF(Seed, Len) = Hash(Seed || 0) || Hash(Seed || 1) ||. . . Hash(Seed || t) Padding string: all 0 x 00 (Optional) Label 00 M m. Len k - 2 h. Len - 2 MGF masked Seed Masked. DB C = (EM)e mod n 15

Diffie-Hellman / El. Gamal-type Systems v Domain parameter generation Ø Based on the hardness of DLP Ø Generate a large (1024 bits or more) prime p Ø Find a generator g that generates the cyclic group Zp* Ø Domain parameter = {p, g} v Key generation Ø Pick a random integer x [1, p-1] Ø Compute y = gx mod p Ø Public key (p, g, y) : publish Ø Private key x : keep secret v Applications Ø Public key encryption Ø Digital signatures Ø Key agreement 16

El. Gamal Encryption Scheme v Keys & parameters Ø Domain parameter = {p, g} Ø Choose x [1, p-1] and compute y = gx mod p Ø Public key (p, g, y) Ø Private key x v Encryption: m (C 1, C 2) Ø Pick a random integer k [1, p-1] Ø Compute C 1 = gk mod p Ø Compute C 2 = m yk mod p v Decryption Ø m = C 2 C 1 -x mod p Ø C 2 C 1 -x = (m yk) (gk)-x = m (gx)k (gk)-x = m mod p 17

El. Gamal Encryption Scheme -- Example v Key Generation Ø Let p=23, g=7 Ø Private key x=9 Ø Public key y = gx mod p = 79 mod 23 = 15 v Encryption: m (C 1, C 2) Ø Let m=20 Ø Pick a random number k=3 Ø Compute C 1 = gk mod p = 73 mod 23 = 21 Ø Compute C 2 = m yk mod p = 20 153 mod 23 = 20 17 mod 23 = 18 Ø Send (C 1 , C 2) = (21, 18) as a ciphertext v Decryption Ø m = C 2 / C 1 x mod p = 18 / 219 mod 23 = 18 / 17 mod 23 = 20 18