LECII PE CALCULATOR MATEMATIC Clasa a VIIa ALGEBR

LECŢII PE CALCULATOR MATEMATICĂ Clasa a VII-a ALGEBRĂ Semestrul I Realizat de prof. TIT CUPRIAN Tit Cuprian – Sarichioi - 2008

NUMERE REALE Tit Cuprian – Sarichioi - 2008

RĂDĂCINA PĂTRATĂ Patratul unui numar rational este totdeauna pozitiv sau zero (adica nenegativ). DEFINITIE Fie a un numar rational nenegativ (a 0). Numarul nenegativ x se numeste radacina patrata a numarului a daca x 2 = a. Notam radacina patrata a numarului a cu EXEMPLE Tit Cuprian – Sarichioi - 2008 .

ALGORITMUL DE EXTRAGERE A RĂDĂCINII PĂTRATE Sa calculam radacina patrata a lui 55225. Despartim numarul in grupe de cate doua cifre, de la dreapta spre stanga Ne intrebam: care este cel mai mare numar al carui patrat este mai mic sau egal cu 5. Acesta este 2; il scriem in dreapta sus; Il ridicam la patrat, obtinem 4 si-l trecem sub 5, aflam restul scaderii 1. Coboram grupul de urmatoarele 2 cifre langa rest. Dublam pe 2 si rezultatul 4 il trecem sub 2. Ne gandim care cifra punem alaturi de 4 si rezultatul il inmultim cu cifra aleasa astfel incat numarul dat sa se cuprinda in 152. Acesta poate este 3 si facem calculele. Rezultatul fiind 129, il trecem sub 152 si aflam restul scaderii. 55225 23 5 4 4 3 3=129 152 46 5 5=2325 129 =2325 ==== Cifra 3 o trecem la rezultat, alaturi de 2. Coboram urmatoare grupa de cifre, pe 25, langa restul 23. Coboram dublul lui 23, care este 46. Ne gandim care cifra punem alturi de 46, numarul format Il inmultim cu acea cifra iar rezultatul sa fie mai mic sau egal cu 2325. Acesta poate fi 5 si facem calculele. Trecem rezultatul 2325 sub numarul 2325 si efectuam scaderea. Asadar radical din 55225 este egal cu 235. Restul fiind zero, algoritmul s-a terminat, cifra 5 o trecm la rezultat alaturi de 23. Tit Cuprian – Sarichioi - 2008 .

MULŢIMEA NUMERELOR REALE Multimea numerelor naturale N = {0; 1; 2; 3; 4; …. } Multimea numerelor intregi Z = {…, -3; -2; -1; 0; +1; +2; +3; …} Multimea numerelor rationale Multimea numerelor irationale Numerele irationale sunt numere care in exprimarea zecimala au partea zecimala infinita si neperiodica. Exemple de numere irationale: Simbolul multimii numerelor irationale: Fie multimea N Z Z Q R R–Q Tit Cuprian – Sarichioi - 2008 .

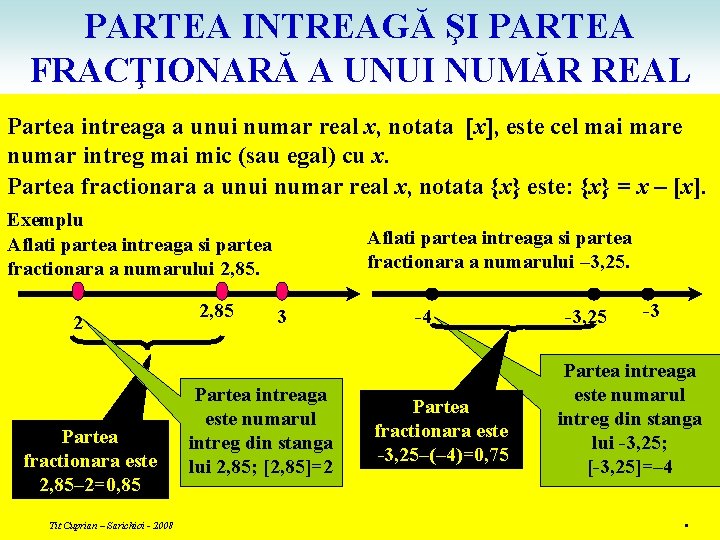
PARTEA INTREAGĂ ŞI PARTEA FRACŢIONARĂ A UNUI NUMĂR REAL Partea intreaga a unui numar real x, notata x , este cel mai mare numar intreg mai mic (sau egal) cu x. Partea fractionara a unui numar real x, notata {x} este: {x} = x – [x]. Exemplu Aflati partea intreaga si partea fractionara a numarului 2, 85. 2 Partea fractionara este 2, 85– 2=0, 85 Tit Cuprian – Sarichioi - 2008 2, 85 Aflati partea intreaga si partea fractionara a numarului – 3, 25. 3 Partea intreaga este numarul intreg din stanga lui 2, 85; [2, 85]=2 -4 Partea fractionara este -3, 25–(– 4)=0, 75 -3, 25 -3 Partea intreaga este numarul intreg din stanga lui -3, 25; [-3, 25]=– 4.

ORDONAREA, OPUSUL SI Dintre doua numere. MODULUL reale diferite, x si y, este mai IN mare cel care se afla R reprezentat la dreapta pe axa numerelor reale. - + y Daca x x > y sau y < x x > y sau x = y spunem ca x este mai mare sau egal cu y si notam x y. Doua numere reale sunt opuse daca sunt coordonatele a doua puncte diferite de pe axa numerelor, egal departate de origine. -a O +a +a + (-a) = 0 Modulul unui numar real x, notat x , este distanta de la origine la punctul ce-l reprezinta pe o axa a numerelor. Tit Cuprian – Sarichioi - 2008 .

REGULI DE CALCUL: PROPRIETATE EXEMPLU Tit Cuprian – Sarichioi - 2008 .

SCOATEREA FACTORILOR DE SUB RADICAL Spre exemplu sa scoatem factorul de sub 1. Se descompune in factori primi numarul dat. 2. Dintr-o pereche de numere prime, iese de sub radical ca factor, un singur factor. 2 2 3 3. De sub radical va iesi sub radical va ramane Tit Cuprian – Sarichioi - 2008 si 864 432 216 108 54 27 9 3 1 2 2 2 3 3 3 2 2 3 .

INTRODUCEREA FACTORILOR SUB RADICAL Regula de introducere a factorilor sub radical: Observatie: sub radical se introduc doar factori pozitivi. EXEMPLE Aceste exercitii pot ajuta la compararea numerelor irationale. Comparati numerele: Se introduc factorii sub radical si obtinem: Prin compararea numerelor de sub radicali, obtinem: Tit Cuprian – Sarichioi - 2008 .

ADUNAREA ŞI SCĂDEREA RADICALILOR Pentru a aduna/scadea mai multe numere reale de forma care au acelasi numar sub radical, se aduna/scad factorii din fata radicalilor, iar rezultatul se inmulteste cu radicalul. EXEMPLUL 1. EXEMPLUL 2. Tit Cuprian – Sarichioi - 2008 .

INMULTIREA SI IMPARTIREA Produsul numerelor reale este numarul real RADICALILOR deci EXEMPLU: Catul numerelor reale deci este numarul real EXEMPLU: 5 8 1 Tit Cuprian – Sarichioi - 2008 1

PUTEREA UNUI NUMĂR REAL ( sub forma de radical ) Tit Cuprian – Sarichioi - 2008 .

MEDIA GEOMETRICĂ SAU MEDIA PROPORŢIONALĂ DEFINITIE. Media geometrica sau proportionala a doua numere nenegative este egala cu cu radacina patrata din produsul lor. PR OP RI ET AT E. Daca 0 a b, atunci: EXEMPLUL 1. Aflati media geometrica a numerelor 7 si 28. Tit Cuprian – Sarichioi - 2008 Cu proprietatea ca a 0 si b 0. EXEMPLUL 2. Daca media geometrica a doua numere este 12, unul din numere este 8, aflati celalalt numar. .

RAŢIONALIZAREA NUMITORILOR Daca numitorul unui raport de numere reale este un numar irational de forma prin amplificarea raportului cu numitorul devine un numar rational si spunem ca am rationalizat numitorul. EXERCITIU REZOLVAT: Rationalizati fractia: Tit Cuprian – Sarichioi - 2008 Rezolvare: este necesar a amplifica fractia cu

VREAU SĂ MĂ MAI UIT INCĂ ODATĂ! SFARSIT