Lec 8 Real gases specific heats internal energy




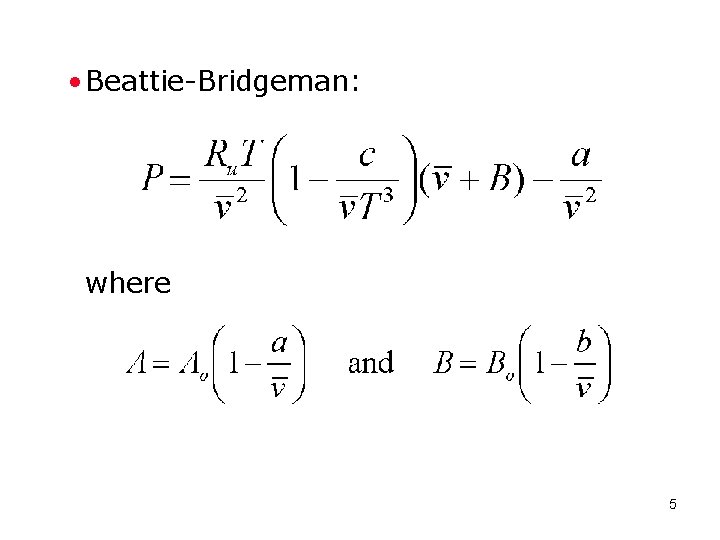






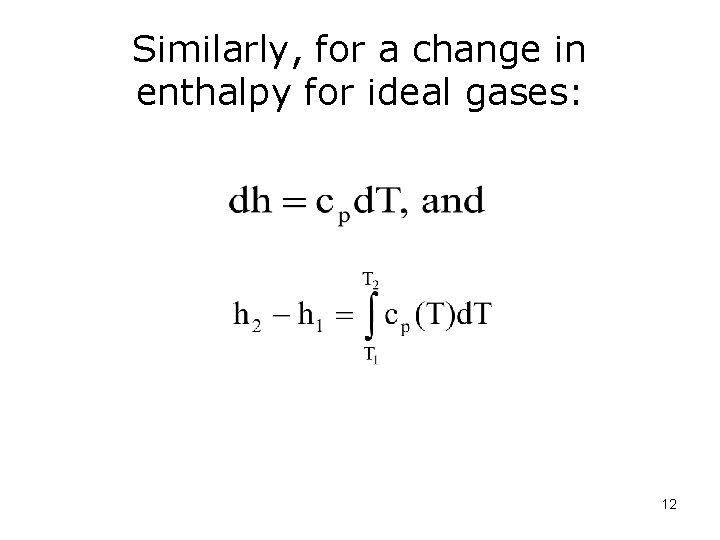
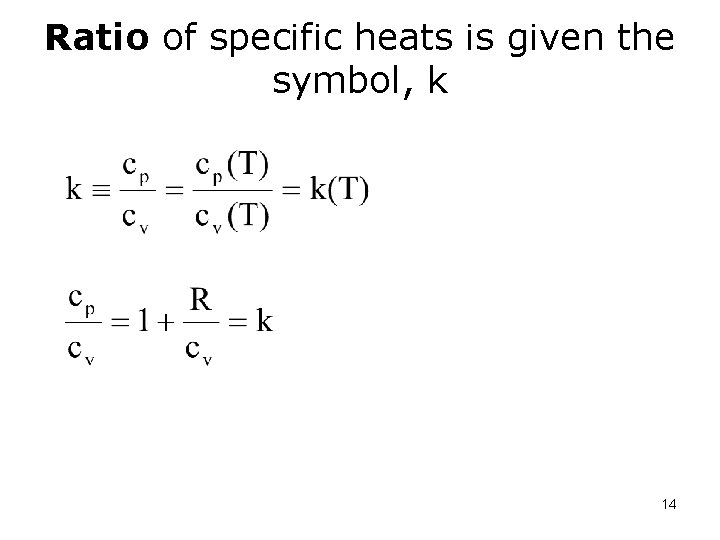
















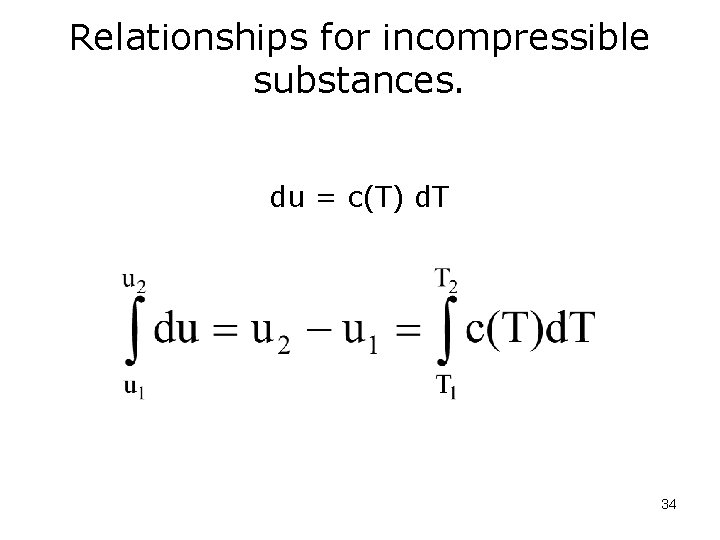


- Slides: 36

Lec 8: Real gases, specific heats, internal energy, enthalpy 1

• For next time: – Read: § 4 -1 to 4 -4 • Outline: – Real gases (Compressibility factor) – Specific heats – Special relationships for ideal gases • Important points: – How to manipulate the ideal gas law – Energy relationships to specific heats – How to evaluate properties of ideal gases 2

TEAMPLAY Under what conditions is it appropriate to apply the ideal gas equation of state? 3

Besides compressibility factor, we can also use more complex equations of state • Van der Waals 4
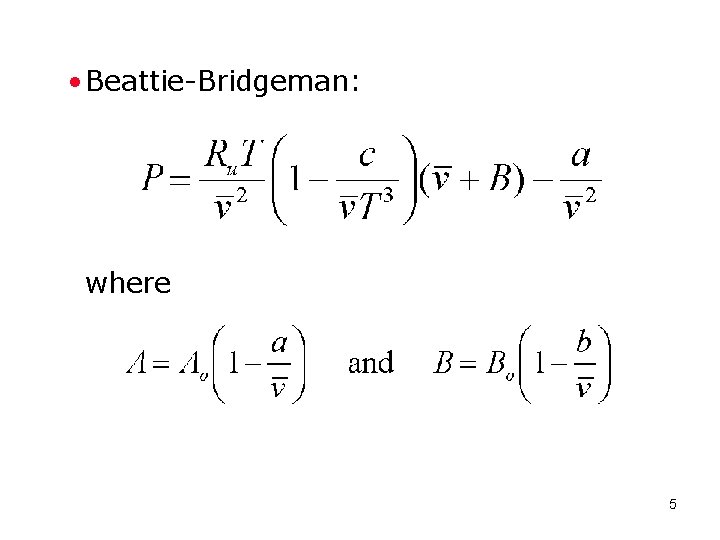
• Beattie-Bridgeman: where 5

Specific Heats Another set of properties that is a common combination of properties are the specific heats. They show up often. For simple compressible systems, these are: 6

Specific Heats • cv is called the “constant volume” specific heat • cp is called the “constant pressure” specific heat • These names tell you how they are determined or measured. • These names do not limit the applicability of them to either constant volume or constant pressure processes. 7

Specific Heats • In general, the specific heats are functions of two variables for simple, compressible systems. • However, we will show that for ideal gases, solids and liquids, they are functions of temperature alone 8

Specific Heats and Ideal Gases: • Joule conducted some experiments where he found that the internal energy, u, was only a function of temperature, u = u(T). • It was independent of P or v. • This implies that cv is also only a function of temperature for an ideal gas: 9

We can start with du and integrate to get the change in u: Note that cv does change with temperature and cannot be automatically pulled from the integral. 10

Let’s look at enthalpy for an ideal gas: • h = u + pv where pv can be replaced by RT because pv = RT. • Therefore, h = u + RT => since u is only a function of T, R is a constant, then h is also only a function of T • so h = h(T) 11
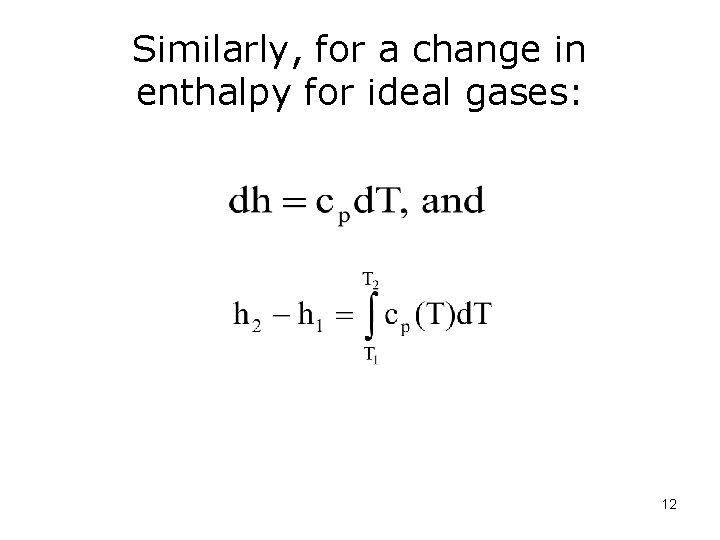
Similarly, for a change in enthalpy for ideal gases: 12

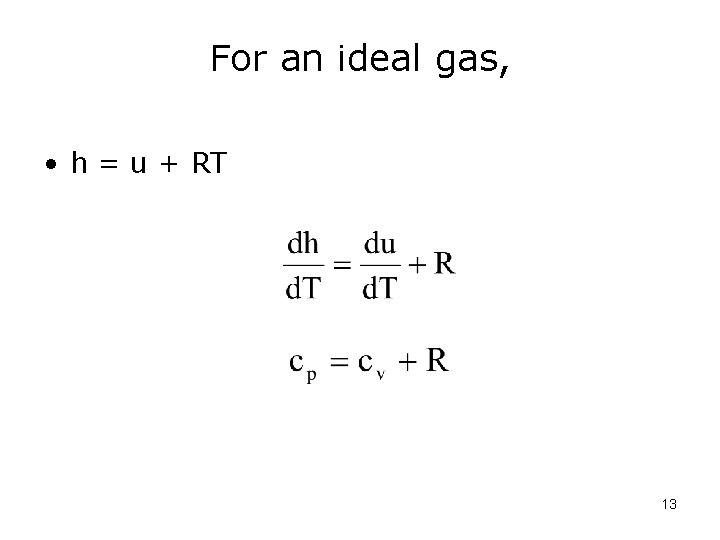
For an ideal gas, • h = u + RT 13
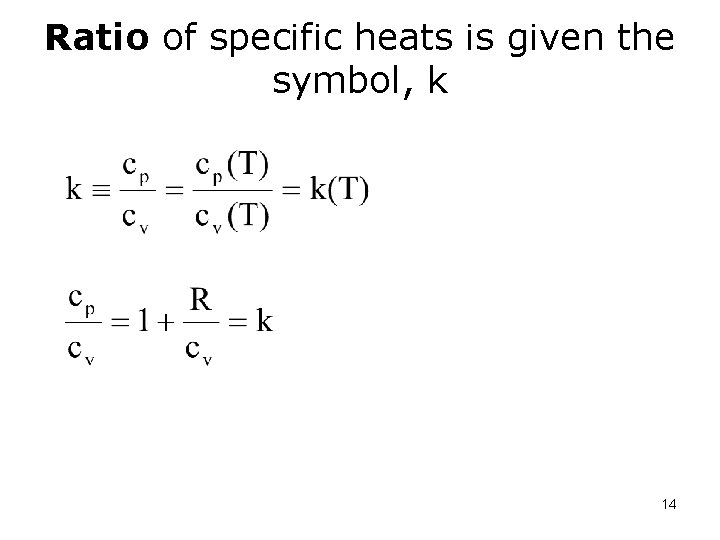
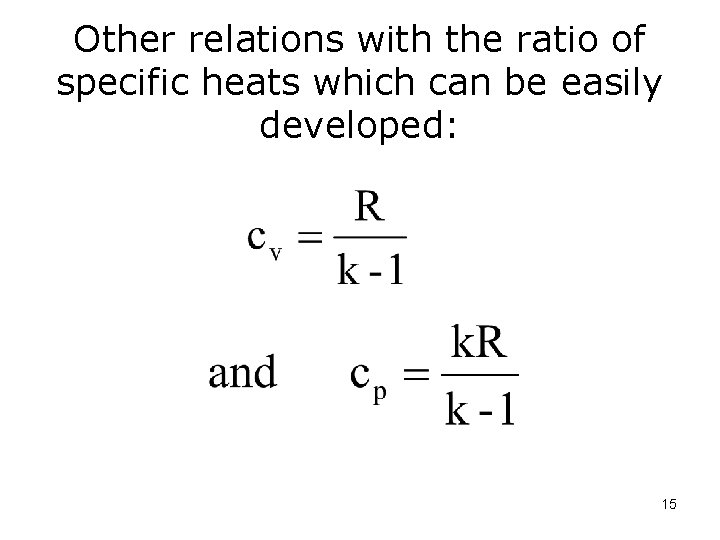
Ratio of specific heats is given the symbol, k 14

Other relations with the ratio of specific heats which can be easily developed: 15

For monatomic gases, 16

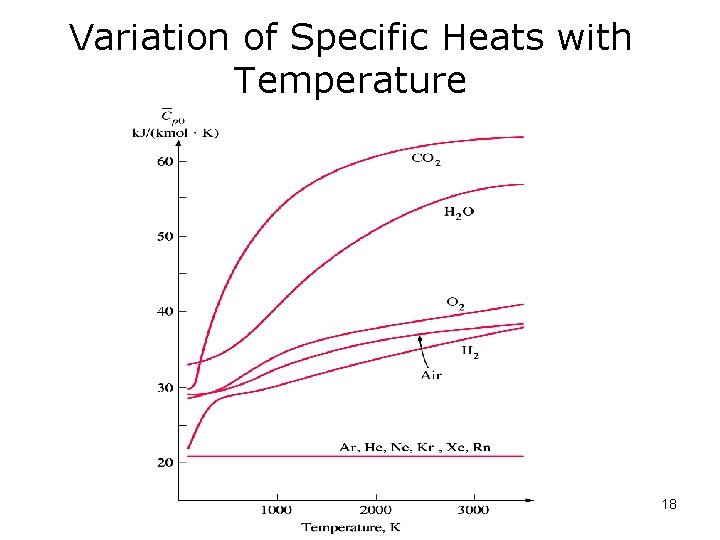
For all other gases, • cp is a function of temperature and it may be calculated from equations such as those in Table A-2 and A-2 E in the appendices • cv may be calculated from cp=cv+R. • Next figure shows the temperature behavior…. many specific heats go up with temperature. 17

Variation of Specific Heats with Temperature 18

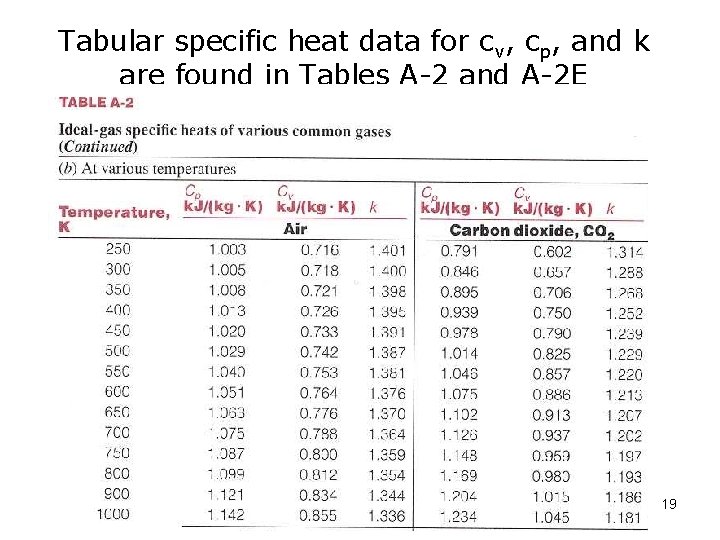
Tabular specific heat data for cv, cp, and k are found in Tables A-2 and A-2 E 19

Assumption of constant specific heats: when can you use it? where Either formulation for cp will be adequate because cp is fairly linear with T over a narrow temperature range. Take your choice. 20

Rule of thumb • Specific heats for ideal gases may be considered to be constant when T 2 -T 1 200 K or 400 °R. • (Note in many cases the temperature range can be significantly larger. ) 21

Changes in enthalpy and internal energy can be calculated from tabular data: • Frequently, we wish to know h 2 -h 1 or u 2 -u 1 and we do not want to go to the trouble to integrate • where cp or cv is a third-degree polynomial in T, as shown in Tables A-2 and A-2 E. 22

The integration is done for us in the ideal gas tables: Tables A-17 and A-17 are for air. Units are mass-based for both h and u. Reference temperature is = 0 K and h = 0 @ Tref = 0 K for ideal gas tables. 23

Example Problem Calculate the change in enthalpy of air for a temperature rise from 300 to 800 K. a) assuming constant specific heats b) using the ideal gas tables 24

Solution For part a), we calculate the enthalpy difference using: Where, 25

Solution - Page 2 For constant specific heats: 26

Solution - Page 3 For variable specific heats, we’ll use the ideal gas air tables 27

Solution - Page 4 So for variable specific heats: Recall for constant specific heats, h = 520 k. J/kg, which is less than 0. 5% difference. 28

Consider incompressible substances • What’s an incompressible substance? – Liquid – Solid • For incompressible substances v = constant dv = 0 29

Incompressible substances Express u = u(T, v) We can take the derivative of u: 0 But dv = 0 for an incompressible substance, so 30

Incompressible substances Recall that Thus: The right hand side is only dependent on temperature. Thus, u = u(T) only for an incompressible substance. 31

Enthalpy of incompressible substances h = u + pv • For an incompressible substance, v=const as before. • If we hold P constant, then we can take ( h/ T)p and show: 32

Specific heats of incompressible substances: cp cv Bottom line: cp = cv = c for an incompressible substance. 33
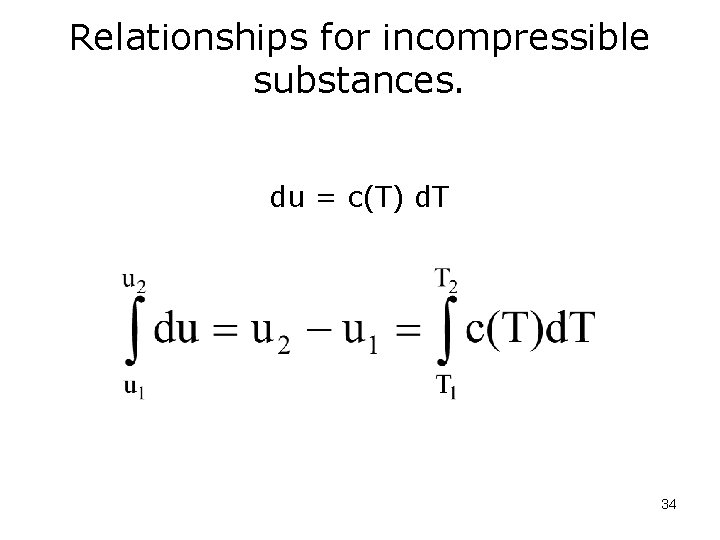
Relationships for incompressible substances. du = c(T) d. T 34

Relationships for incompressible substances. We can also show that: 35

Relationships for incompressible substances • Now, if the temperature range is small enough, say up to about 200 K (400 °F), then c may be regarded as a constant, and • u 2 - u 1=c(T 2 - T 1) • and h 2 - h 1=c(T 2 - T 1)+v(p 2 - p 1) 36