Leastsquare collocation in geoid determination Reporter Duong Thanh

Least-square collocation in geoid determination Reporter: Duong Thanh Trung Student ID: P 68987015 Duong Thanh Trung, Department of Geomatics, NCKU 1

Outline n n n n Introduction Principles of prediction Least square collocation (LSC) Least square collocation of functions Least square collocation with noise Application of LSC to Geoid determination Simulation program Duong Thanh Trung, Department of Geomatics, NCKU 2

Introduction n Geoid determination is one of the important tasks of geodesy q q q n n For research the shape of earth determining geoid height in satellite measurements monitoring sea level changes … To determine geoid model we need to take gravity measurements over the whole earth The fact that we can measure gravitational quantities only at limited points Duong Thanh Trung, Department of Geomatics, NCKU 3

Introduction n To build Geoid model we must estimate gravitational quantities at other points by prediction (interpolation or extrapolation) One useful method used in prediction is leastsquare collocation (LSQ) LSQ can be used to estimate gravitational quantities such as g, N, , from variety of measurements. Duong Thanh Trung, Department of Geomatics, NCKU 4

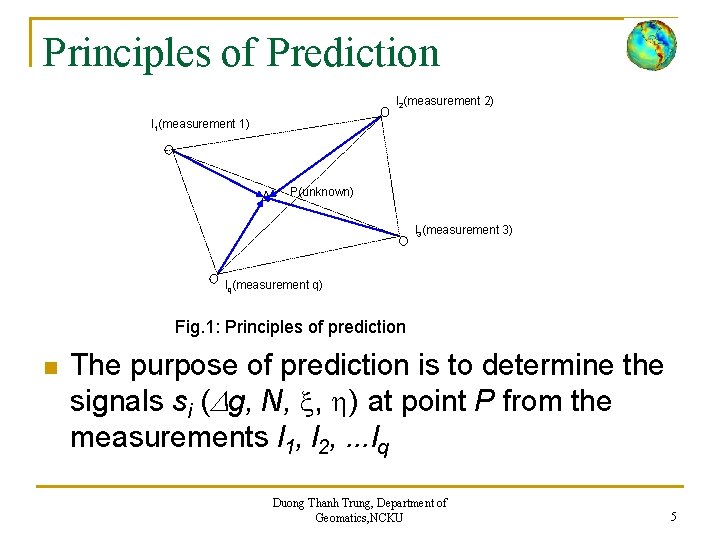
Principles of Prediction l 2(measurement 2) l 1(measurement 1) P(unknown) l 3(measurement 3) lq(measurement q) Fig. 1: Principles of prediction n The purpose of prediction is to determine the signals si ( g, N, , ) at point P from the measurements l 1, l 2, . . . lq Duong Thanh Trung, Department of Geomatics, NCKU 5

Principles of Prediction n The linear estimation for s form as n H is matrix of coefficients approximated by a linear combination of l The error vector is The covariance matrix is determined by n n Duong Thanh Trung, Department of Geomatics, NCKU 6

Principles of Prediction n After some transformations we get n n We need to choose H in which the C is minimum That means Now the estimated value is n With covariance error is n Duong Thanh Trung, Department of Geomatics, NCKU 7

Principles of Prediction n Where q C(P, Q) is called covariance function between two points P and Q and can be determined in term of spherical harmonic n In some cases it is determined empirically in analytical expression by Hirvonen (1962) or Tscherning (1967) Duong Thanh Trung, Department of Geomatics, NCKU 8

Least square collocation (LSC) n The determination of a function by fitting an analytical approximation to a certain number of given linear functions is called collocation. The present method for determining the gravitational field by least square prediction is called Least Square Collocation [2] Duong Thanh Trung, Department of Geomatics, NCKU 9

Least square collocation Assume that we have q measured values which are linear functional of the anomalous potential T. q some of popular quantities are: q In general case, they are denoted by In matrix form Duong Thanh Trung, Department of Geomatics, NCKU 10

Least square collocation q n Now, we can find T from q linear functions Li. T Where are called covariance propagation Duong Thanh Trung, Department of Geomatics, NCKU 11

Least square collocation of functions n In more general cases we can estimate arbitrary signals that is anomalous gravitational field S =ST = SPT(P) And error covariance matrix Duong Thanh Trung, Department of Geomatics, NCKU 12

Least square collocation with noise n If the measurement li are affected by random errors n The prediction formula become (by Moritz. H. 1980) n Where: Duong Thanh Trung, Department of Geomatics, NCKU 13

Application to geoid determination n n Determine the geoidal height N from measurements of gravity anomalies g and deflection of vertical , . Since N is linear with T, we can estimate s=N(P) by collocation Duong Thanh Trung, Department of Geomatics, NCKU 14

Application to geoid determination The components of Covariance matrix is determined by covariance propagation described by Moritz. H 1980 P 108 Duong Thanh Trung, Department of Geomatics, NCKU 15

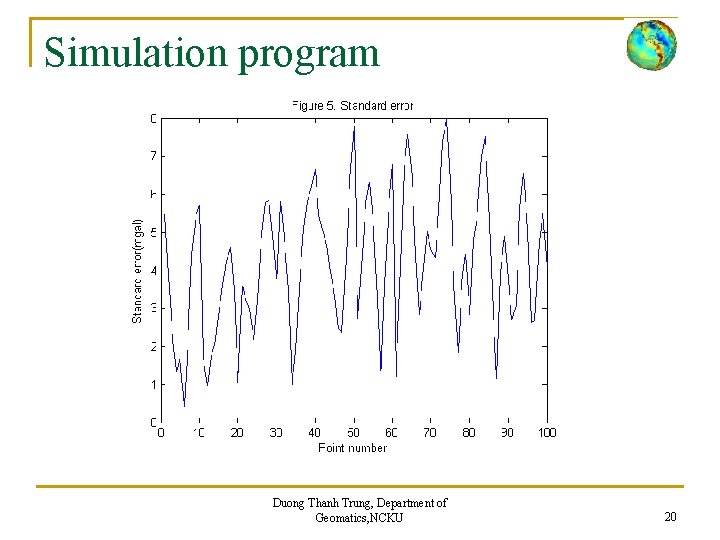
Simulation program n n The purpose of the program is to estimate anomaly g at every grid point from the measured gravity anomalies g 1, g 2, . . . gn in a given area Building a gravity anomalies map as well as perform estimated errors at these points Program is written on matlab language Use the simulated data Duong Thanh Trung, Department of Geomatics, NCKU 16

Simulation program Fig. 3. Estimate gravity anomaly at grid ponts Duong Thanh Trung, Department of Geomatics, NCKU 17

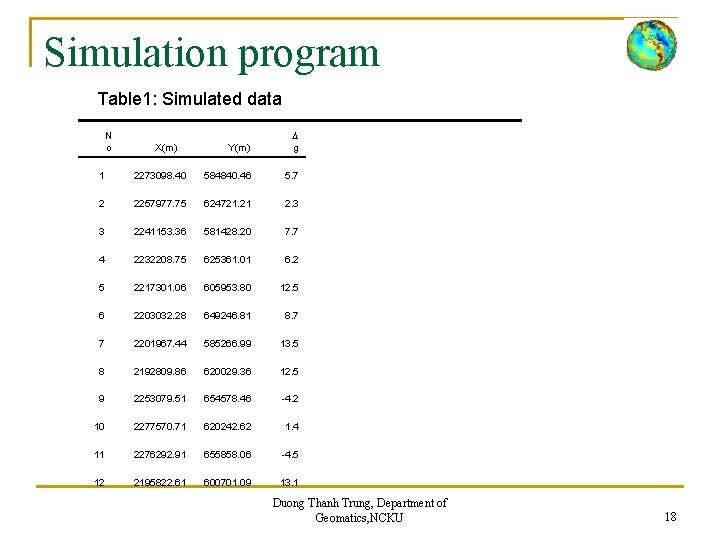
Simulation program Table 1: Simulated data N o X(m) Y(m) D g 1 2273098. 40 584840. 46 5. 7 2 2257977. 75 624721. 21 2. 3 3 2241153. 36 581428. 20 7. 7 4 2232208. 75 625361. 01 6. 2 5 2217301. 06 605953. 80 12. 5 6 2203032. 28 649246. 81 8. 7 7 2201967. 44 585266. 99 13. 5 8 2192809. 86 620029. 36 12. 5 9 2253079. 51 654578. 46 -4. 2 10 2277570. 71 620242. 62 1. 4 11 2276292. 91 655858. 06 -4. 5 12 2195822. 61 600701. 09 13. 1 Duong Thanh Trung, Department of Geomatics, NCKU 18

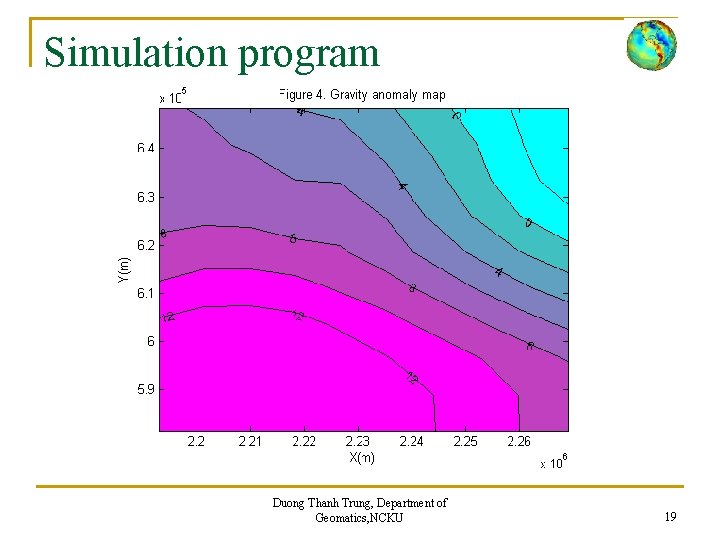
Simulation program Duong Thanh Trung, Department of Geomatics, NCKU 19

Simulation program Duong Thanh Trung, Department of Geomatics, NCKU 20

Conclusions n Although there are have some global geoid models, the establishment of local geoid model is still necessary in certain regions for many accurate geodesy purposes n Least square collocation is still a useful method for geoid model determination n By the development of satellite geodesy, variety of gravitational measurements can be taken and combined in calculating for geoid determination q It requires improving exiting methods or developing new theories to solve complicate combinations. q Requires the development of new softwares strong enough for automatic computation Duong Thanh Trung, Department of Geomatics, NCKU 21

References n n n [1]. Hofmann-Wellenhof, B. and H. Moritz, (2006) [2]. Moritz. H, ”Advanced Physical Geodesy” (1980) [3]. Jonh W. Robbins, “Least square collocation applied to local gravimetric solutions from satellite gravity gradiometry data” (1985) [4]. C. C. Tscherning: Testing griding and filtering of GOCE gradiometer data by least square collocation using simulated data [5]. C. C. Tscherning: Geoid determination by leastsquares collocation using GRAVSOFT Duong Thanh Trung, Department of Geomatics, NCKU 22

Thank you for your attention Reporter: Duong Thanh Trung Student ID: P 68987015 Duong Thanh Trung, Department of Geomatics, NCKU 23