Least Squares Regression Line u Regression line equation








- Slides: 10

Least Squares Regression Line u Regression line equation: ^ y = a + bx – x is the value of the explanatory variable – “y-hat” is the predicted value for a x value – a and b are just the intercept and slope of a straight line Essential Statistics Chapter 5 1

Regression Line Calculation u. Regression equation: ^ y = a + bx where sx and sy are the standard deviations of the two variables, and r is their correlation Essential Statistics Chapter 5 2

R-square 2 (R ) To assess how well regression equation (a model) explain and predicts future outcomes u R-square value (0 ≤ r 2 ≤ 1) u In model analysis, measuring the accuracy of regression equation ◙ value of 1 indicates a reliable model for future prediction ◙ value of zero indicates the model fails. u Essential Statistics Chapter 5 3

Coefficient of Determination 2 (R ) u In linear regression, R 2 is the square of the sample correlation coefficient u R 2 or r 2 is the fraction of the explained variation to the total variation in the values of the response variable (y) ◙ r=1: r 2=1: regression line explains all (100%) of the variation in y ◙ r=. 7: r 2=. 49: regression line explains almost half (50%) of the variation in y Essential Statistics Chapter 5 4

Residuals u. A residual is the difference between an observed value of the response variable and the value predicted by the regression line: residual = y Essential Statistics Chapter 5 ^y 5

Measuring Strength & Direction of a Linear Relationship u The correlation coefficient r – measure of the strength of the relationship: the stronger the relationship, the larger the magnitude of r. – measure of the direction of the relationship: positive r indicates a positive relationship, negative r indicates a negative relationship. Essential Statistics Chapter 4 6

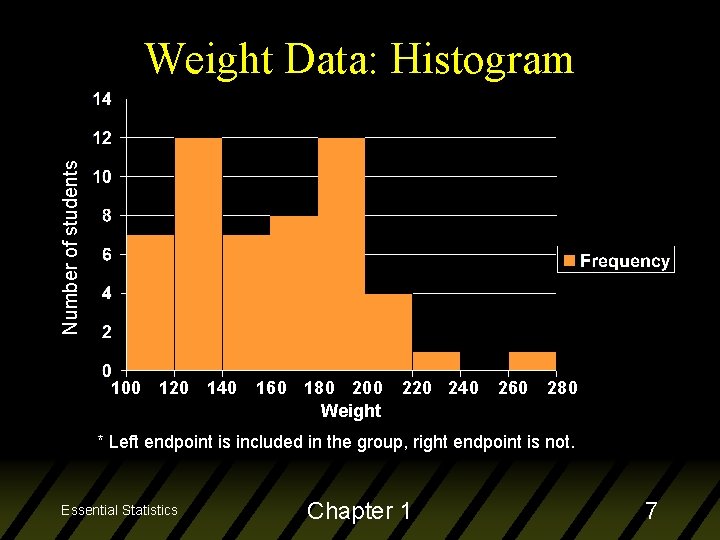
Number of students Weight Data: Histogram 100 120 140 160 180 200 Weight 220 240 260 280 * Left endpoint is included in the group, right endpoint is not. Essential Statistics Chapter 1 7

Weight Data: Stemplot (Stem & Leaf Plot) Key 20|3 means 203 pounds Stems = 10’s Leaves = 1’s Essential Statistics Chapter 1 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0166 009 0034578 00359 08 00257 555 000255 000055567 245 3 025 0 0 8

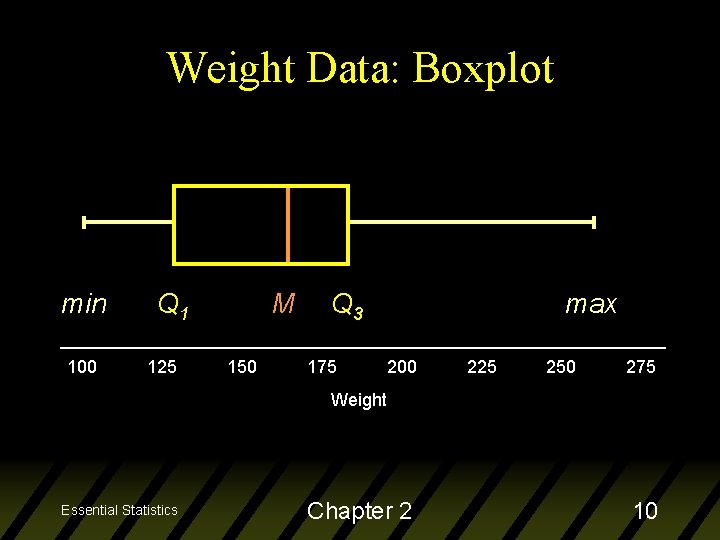
Five-Number Summary u minimum = 100 u Q 1 = 127. 5 u M = 165 u Q 3 = 185 u maximum = 260 The middle 50% of the data are between Q 1 and Q 3 Essential Statistics Chapter 2 9

Weight Data: Boxplot min 100 Q 1 125 M 150 Q 3 175 max 200 225 250 275 Weight Essential Statistics Chapter 2 10