Learning Uncertainty and Information Learning Parameters Big Ideas

Learning, Uncertainty, and Information: Learning Parameters Big Ideas November 10, 2004

Roadmap • Noisy-channel model: Redux • Hidden Markov Models – The Model – Decoding the best sequence – Training the model (EM) • N-gram models: Modeling sequences – Shannon, Information Theory, and Perplexity • Conclusion

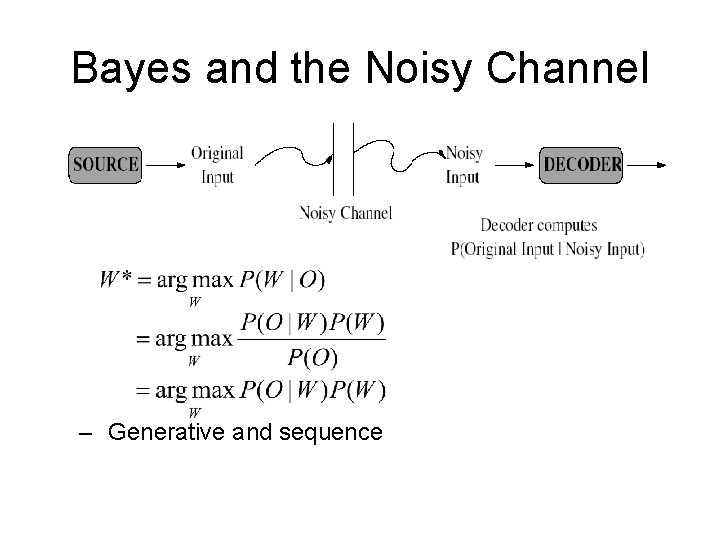
Bayes and the Noisy Channel – Generative and sequence

Hidden Markov Models (HMMs) • An HMM is: – 1) A set of states: – 2) A set of transition probabilities: • Where aij is the probability of transition qi -> qj – 3)Observation probabilities: • The probability of observing ot in state i – 4) An initial probability dist over states: • The probability of starting in state i – 5) A set of accepting states

Three Problems for HMMs • Find the probability of an observation sequence given a model – Forward algorithm • Find the most likely path through a model given an observed sequence – Viterbi algorithm (decoding) • Find the most likely model (parameters) given an observed sequence – Baum-Welch (EM) algorithm

Learning HMMs • Issue: Where do the probabilities come from? • Supervised/manual construction • Solution: Learn from data – Trains transition (aij), emission (bj), and initial (πi) probabilities • Typically assume state structure is given – Unsupervised

Manual Construction • Manually labeled data – Observation sequences, aligned to – Ground truth state sequences • • • Compute (relative) frequencies of state transitions Compute frequencies of observations/state Compute frequencies of initial states Bootstrapping: iterate tag, correct, reestimate, tag. Problem: – Labeled data is expensive, hard/impossible to obtain, may be inadequate to fully estimate • Sparseness problems

Unsupervised Learning • Re-estimation from unlabeled data – Baum-Welch aka forward-backward algorithm – Assume “representative” collection of data • E. g. recorded speech, gene sequences, etc – Assign initial probabilities • Or estimate from very small labeled sample – Compute state sequences given the data • I. e. use forward algorithm – Update transition, emission, initial probabilities

Updating Probabilities • Intuition: – Observations identify state sequences – Adjust probability of transitions/emissions – Make closer to those consistent with observed – Increase P(Observations|Model) • Functionally – For each state i, what proportion of transitions from state i go to state j – For each state i, what proportion of observations match O? – How often is state i the initial state?

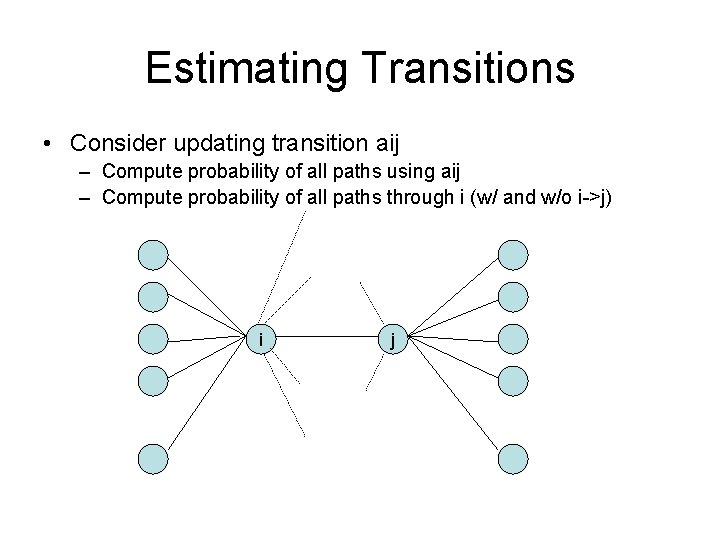
Estimating Transitions • Consider updating transition aij – Compute probability of all paths using aij – Compute probability of all paths through i (w/ and w/o i->j) i j

Forward Probability Where α is the forward probability, t is the time in utterance, i, j are states in the HMM, aij is the transition probability, bj(ot) is the probability of observing ot in state bj N is the max state, T is the last time

Backward Probability Where β is the backward probability, t is the time in sequence, i, j are states in the HMM, aij is the transition probability, bj(ot) is the probability of observing ot in state bj N is the final state, and T is the last time

Re-estimating • Estimate transitions from i->j • Estimate observations in j • Estimate initial i