Learning Target I can use theorems postulates or








- Slides: 28

Learning Target I can use theorems, postulates or definitions to prove that… a. vertical angles are congruent. b. When a transversal crosses parallel lines, alternate interior angles are congruent and corresponding angles are congruent, and sameside interior angles are supplementary.

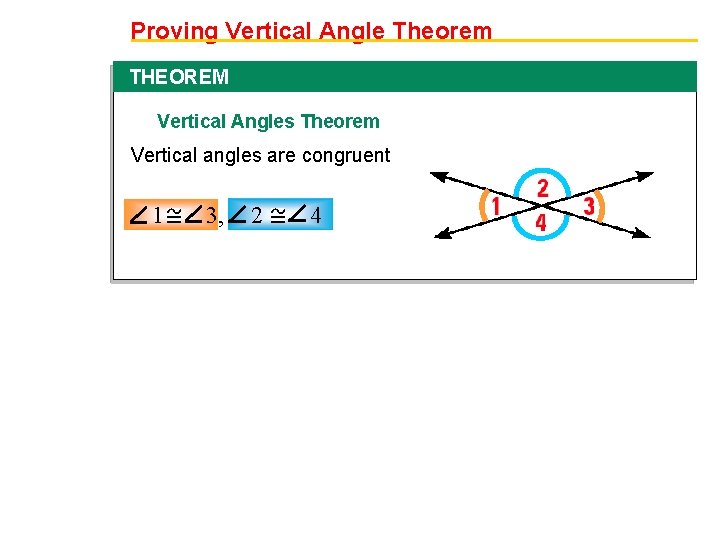
Proving Vertical Angle Theorem THEOREM Vertical Angles Theorem Vertical angles are congruent 1 3, 2 4

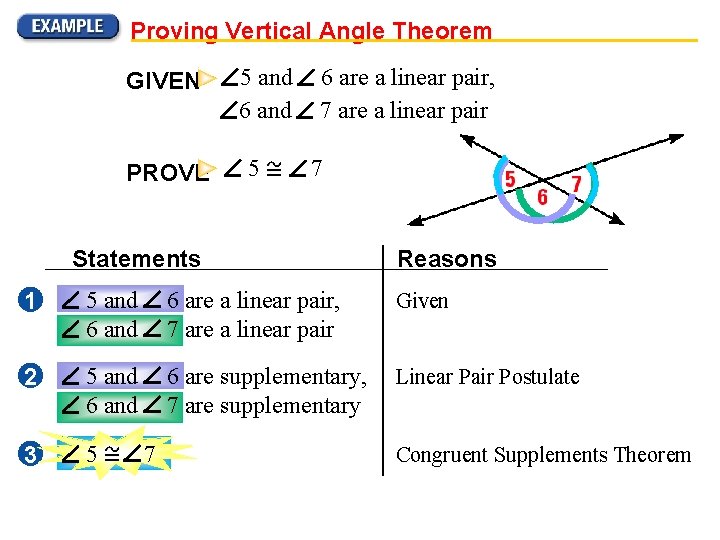
Proving Vertical Angle Theorem GIVEN PROVE 5 and 6 and 5 6 are a linear pair, 7 are a linear pair 7 Statements Reasons 1 5 and 6 are a linear pair, 7 are a linear pair Given 2 5 and 6 are supplementary, 7 are supplementary Linear Pair Postulate 3 5 7 Congruent Supplements Theorem

Third Angles Theorem

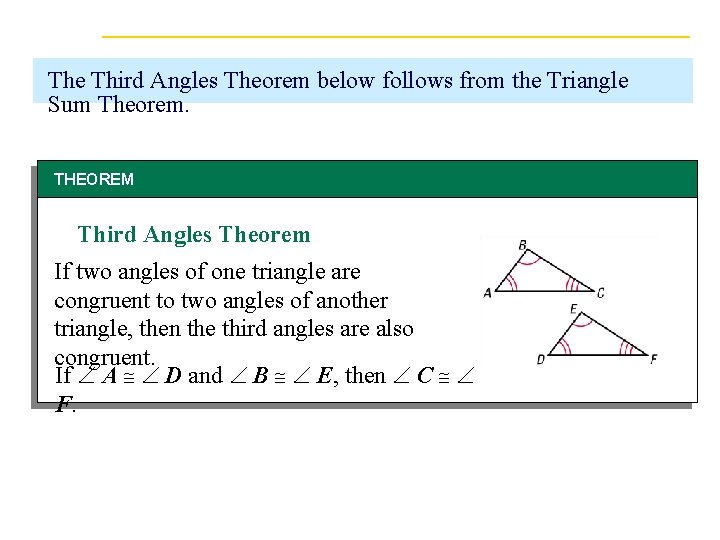
The Third Angles Theorem below follows from the Triangle Sum Theorem. THEOREM Third Angles Theorem If two angles of one triangle are congruent to two angles of another triangle, then the third angles are also congruent. If A D and B E, then C F. Goal 1

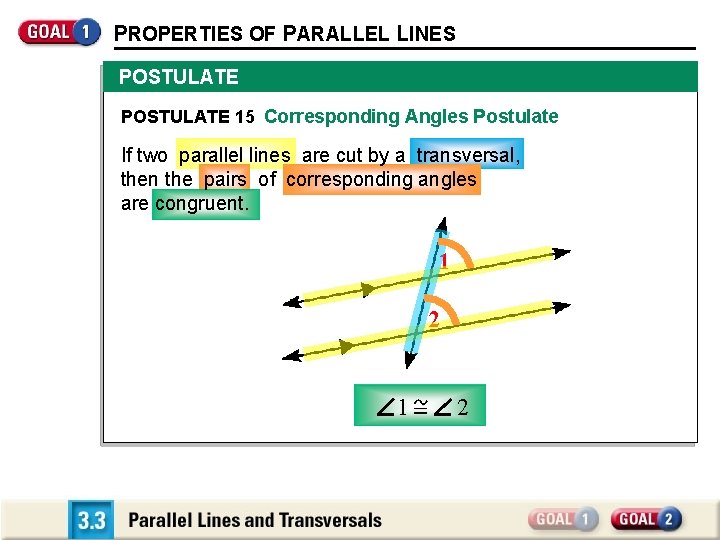
PROPERTIES OF PARALLEL LINES POSTULATE 15 Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. 1 2

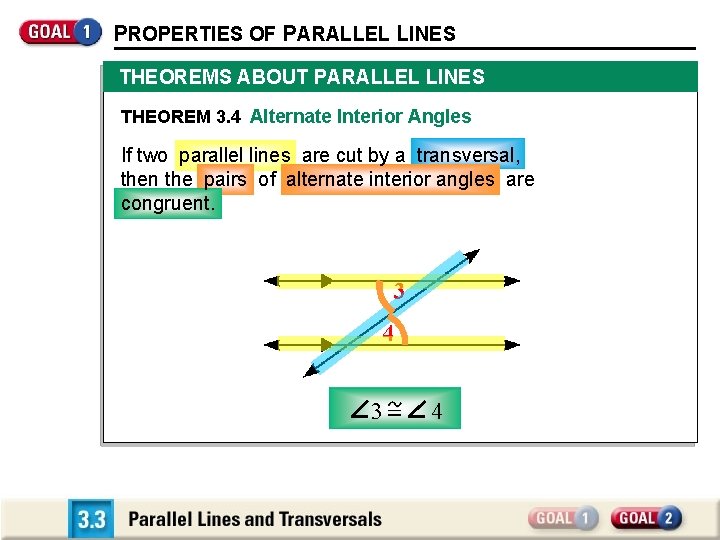
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 4 Alternate Interior Angles If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 3 4

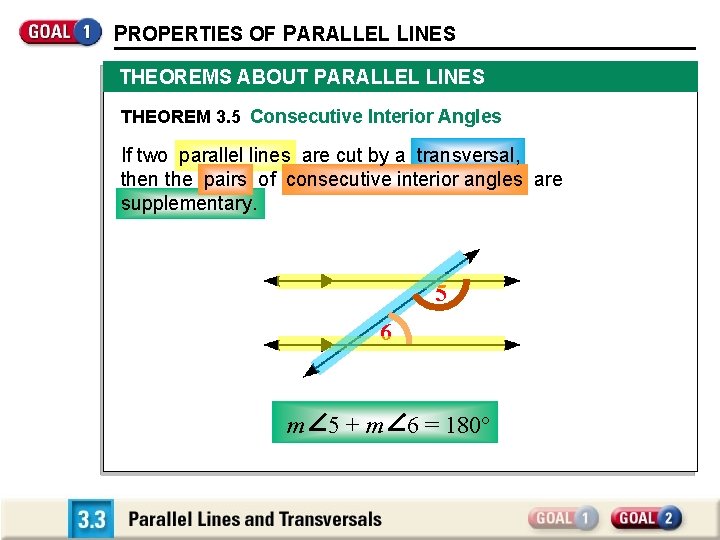
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 5 Consecutive Interior Angles If two parallel lines are cut by a transversal, then the pairs of consecutive interior angles are supplementary. 5 6 m 5+m 6 = 180°

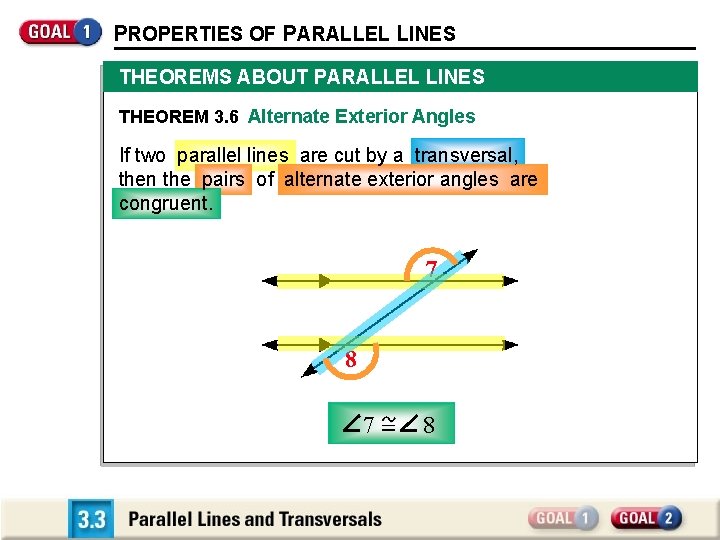
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 6 Alternate Exterior Angles If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent. 7 8

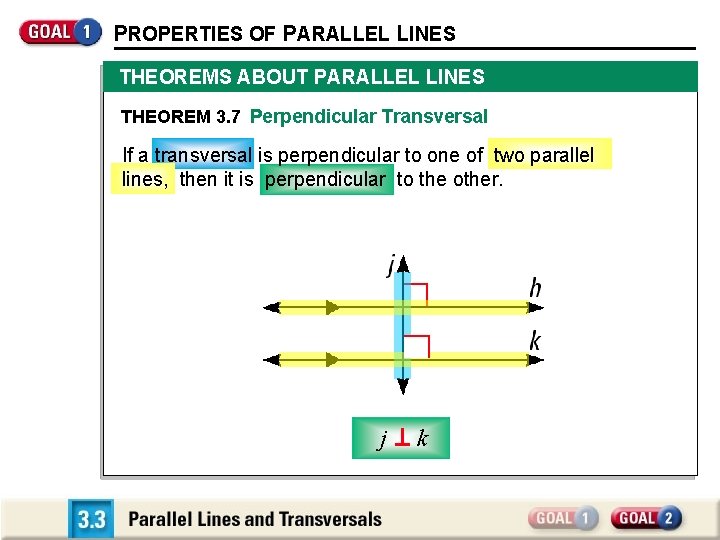
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 7 Perpendicular Transversal If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other. j k

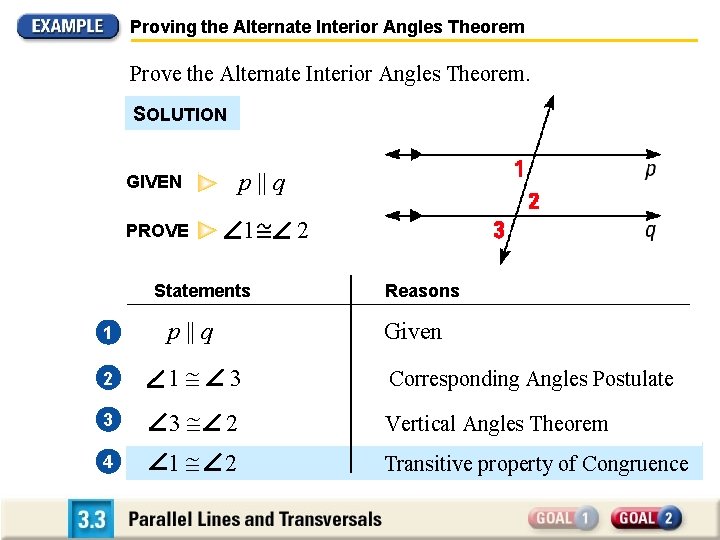
Proving the Alternate Interior Angles Theorem Prove the Alternate Interior Angles Theorem. SOLUTION GIVEN p || q PROVE 1 Statements 2 Reasons 1 p || q Given 2 1 3 Corresponding Angles Postulate 3 3 2 Vertical Angles Theorem 4 1 2 Transitive property of Congruence

Using Properties of Parallel Lines Given that m 5 = 65°, find each measure. Tell which postulate or theorem you use. SOLUTION m 6 = m 5 = 65° m 7 = 180° – m m 8 = m 5 = 65° Corresponding Angles Postulate m 9 = m 7 = 115° Alternate Exterior Angles Theorem Vertical Angles Theorem 5 = 115° Linear Pair Postulate

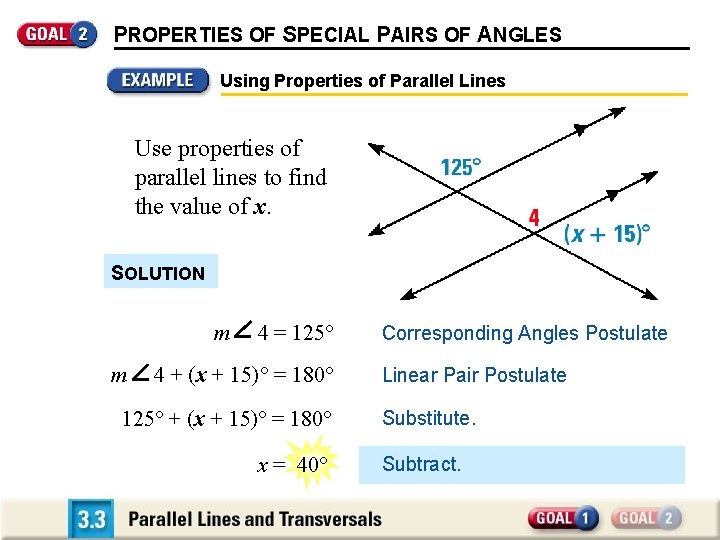
PROPERTIES OF SPECIAL PAIRS OF ANGLES Using Properties of Parallel Lines Use properties of parallel lines to find the value of x. SOLUTION m m 4 = 125° 4 + (x + 15)° = 180° 125° + (x + 15)° = 180° x = 40° Corresponding Angles Postulate Linear Pair Postulate Substitute. Subtract.

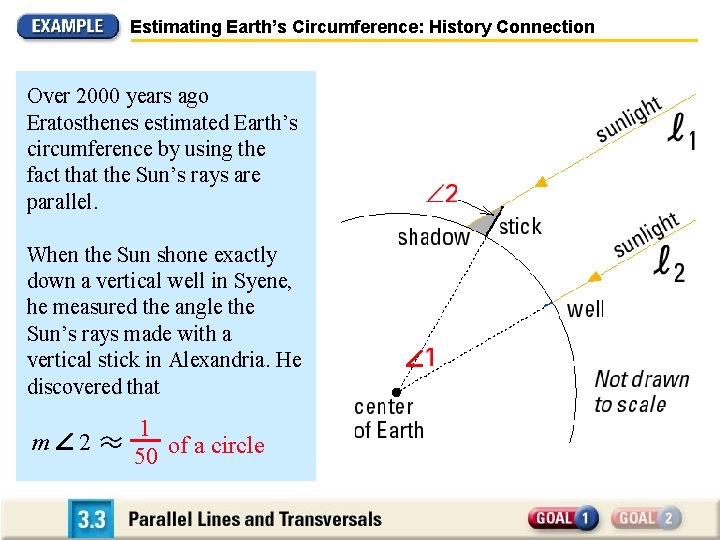
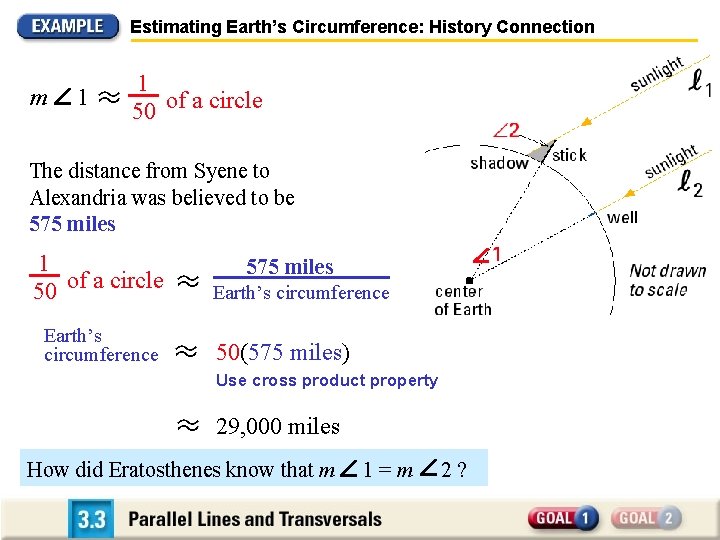
Estimating Earth’s Circumference: History Connection Over 2000 years ago Eratosthenes estimated Earth’s circumference by using the fact that the Sun’s rays are parallel. When the Sun shone exactly down a vertical well in Syene, he measured the angle the Sun’s rays made with a vertical stick in Alexandria. He discovered that m 2 1 50 of a circle

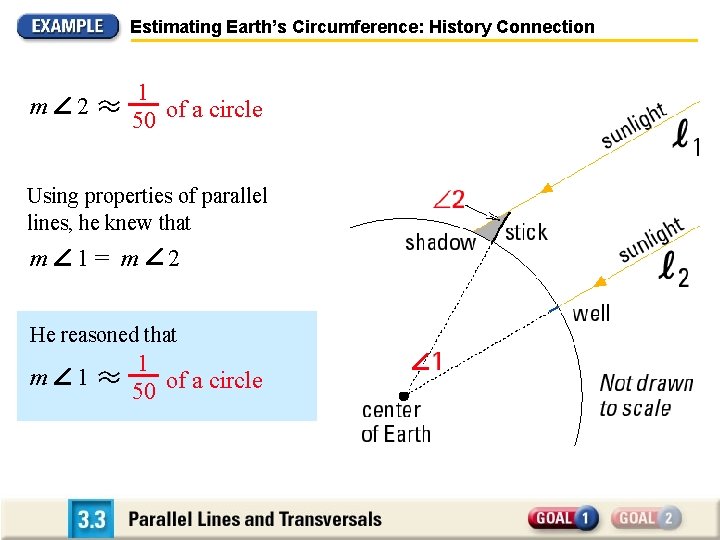
Estimating Earth’s Circumference: History Connection m 2 1 50 of a circle Using properties of parallel lines, he knew that m 1= m 2 He reasoned that m 1 1 50 of a circle

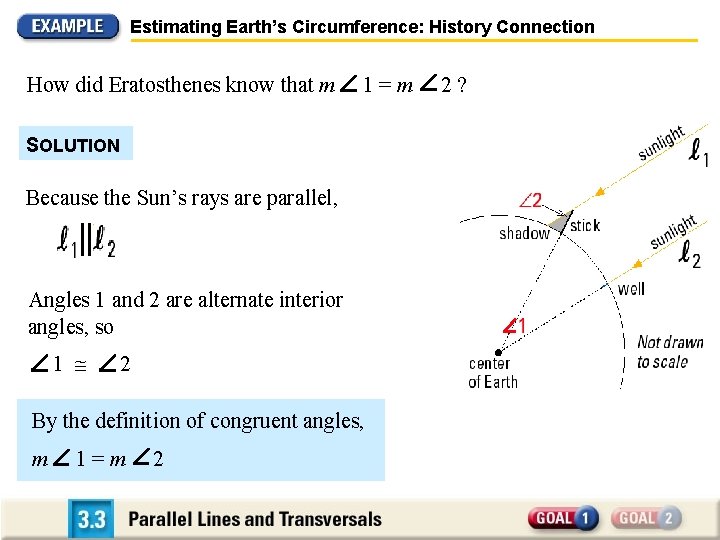
Estimating Earth’s Circumference: History Connection m 1 1 50 of a circle The distance from Syene to Alexandria was believed to be 575 miles 1 50 of a circle Earth’s circumference 575 miles Earth’s circumference 50(575 miles) Use cross product property 29, 000 miles How did Eratosthenes know that m 1=m 2?

Estimating Earth’s Circumference: History Connection How did Eratosthenes know that m 1=m SOLUTION Because the Sun’s rays are parallel, Angles 1 and 2 are alternate interior angles, so 1 2 By the definition of congruent angles, m 1=m 2 2?

Using the Third Angles Theorem Find the value of x. SOLUTIO N In the diagram, N R and L S. From the Third Angles Theorem, you know that So, m M = m T. M the T. Triangle Sum Theorem, m M = 180˚– 55˚ From – 65˚ = 60˚. Third Angles Theorem m M = m T 60˚ = (2 x + 30)˚ Substitute. 30 = 2 x Subtract 30 from each side. 15 = x Divide each side by 2. Example

Learning Target Proving Triangles are Congruent Decide whether the triangles are congruent. Justify your reasoning. SOLUTIO Naragraph Proof P From the diagram, you are given that all three corresponding sides are , NQ and , QR QM RP MN PQ Because P and N have the same measures, P N. By the Vertical Angles Theorem, you know that PQR NQM. By the Third Angles Theorem, R M. So, all three pairs of corresponding sides and all three pairs of corresponding angles are congruent. By the PQR NQM definition of congruent triangles, . Goal 2

Proving Two Triangles are Congruent Prove that AEB DEC . A B E C D GIVEN AB ||DC, AB DC E is the midpoint of BC , and AD. PROVE AEB DEC. Plan for Proof Use the fact that AEB and DEC are vertical angles to show that those angles are congruent. Use the fact that BC intersects parallel segments AB and DC to identify other pairs of angles that are congruent. Example

Proving Two Triangles are Congruent Prove that AEB DEC . A B E SOLUTION D C Statements Reasons AB || DC , AB DC Given EAB EDC, ABE DCE Alternate Interior Angles Theorem AEB DEC Vertical Angles Theorem E is the midpoint of AD, E is the midpoint of BC Given AE DE , BE CE Definition of midpoint AEB DEC Definition of congruent triangles Example

Proving Triangles are Congruent You have learned to prove that two triangles are congruent by the definition of congruence – that is, by showing that all pairs of corresponding angles and corresponding sides are congruent. THEOREM B Theorem 4. 4 Properties of Congruent Triangles A Reflexive Property of Congruent Triangles Every triangle is congruent to itself. Symmetric Property of Congruent Triangles D If ABC DEF , then . DEF ABC Transitive Property of Congruent Triangles If ABC DEF and , ABC then JKL J DEF JKL C E F L . K Goal 2

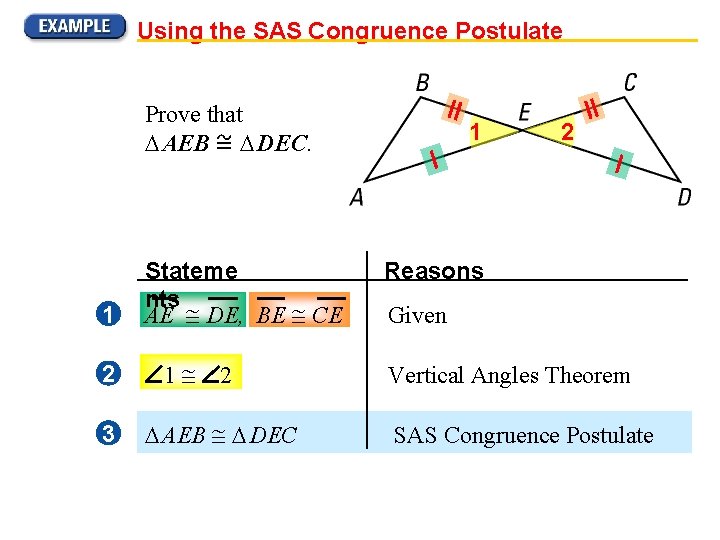
Using the SAS Congruence Postulate Prove that AEB DEC. 1 2 3 Stateme nts AE DE, BE CE 1 2 AEB DEC 1 2 Reasons Given Vertical Angles Theorem SAS Congruence Postulate

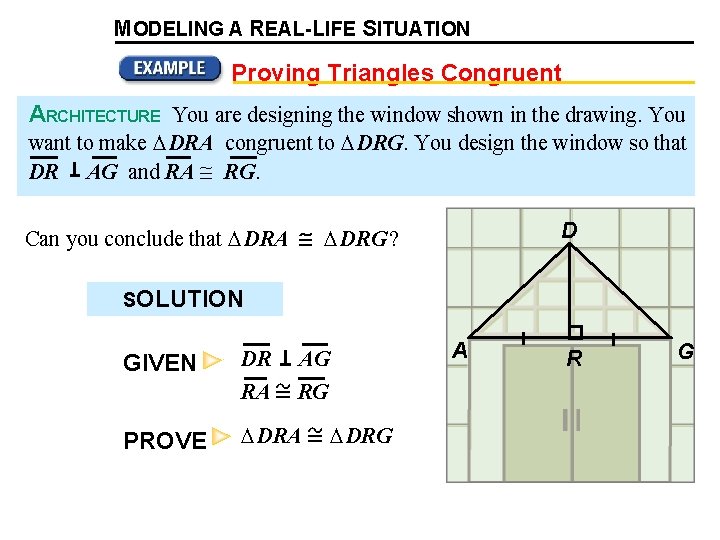
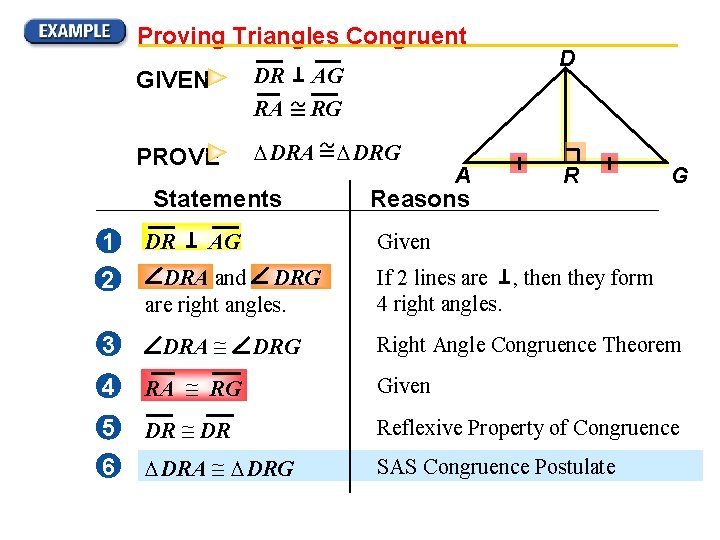
MODELING A REAL-LIFE SITUATION Proving Triangles Congruent ARCHITECTURE You are designing the window shown in the drawing. You want to make DRA congruent to DRG. You design the window so that DR AG and RA RG. D Can you conclude that DRA DRG ? SOLUTION GIVEN DR RA PROVE DRA A AG RG DRG R G

Proving Triangles Congruent GIVEN DR RA AG RG PROVE DRA Statements 1 DR 2 DRA and DRG are right angles. DRG A Reasons D R G Given AG If 2 lines are , then they form 4 right angles. 3 DRA 4 RA RG Given 5 DR Reflexive Property of Congruence 6 DRA DRG SAS Congruence Postulate DRG Right Angle Congruence Theorem

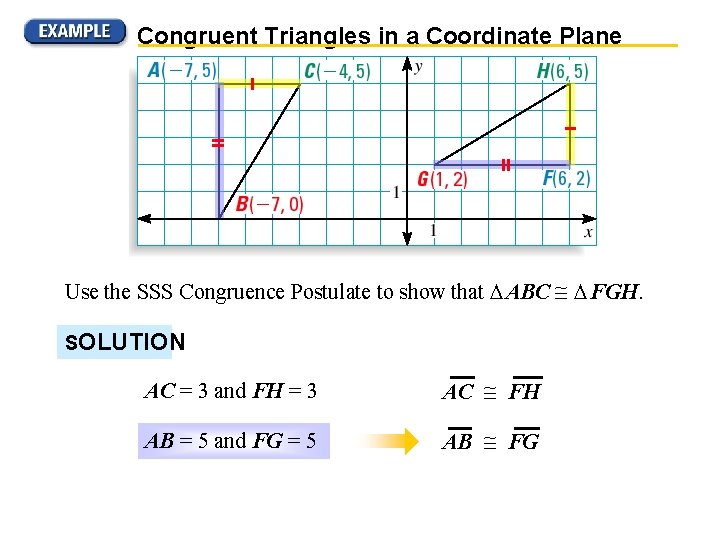
Congruent Triangles in a Coordinate Plane Use the SSS Congruence Postulate to show that ABC FGH. SOLUTION AC = 3 and FH = 3 AC FH AB = 5 and FG = 5 AB FG

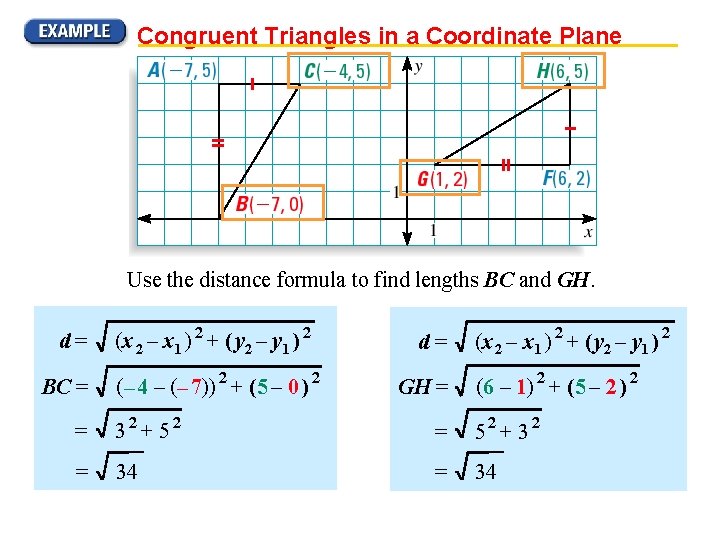
Congruent Triangles in a Coordinate Plane Use the distance formula to find lengths BC and GH. d= BC = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (– 4 – (– 7)) 2 + (5 – 0 ) 2 d= GH = (x 2 – x 1 ) 2 + ( y 2 – y 1 ) 2 (6 – 1) 2 + (5 – 2 ) 2 = 32 + 52 = 52 + 32 = 34

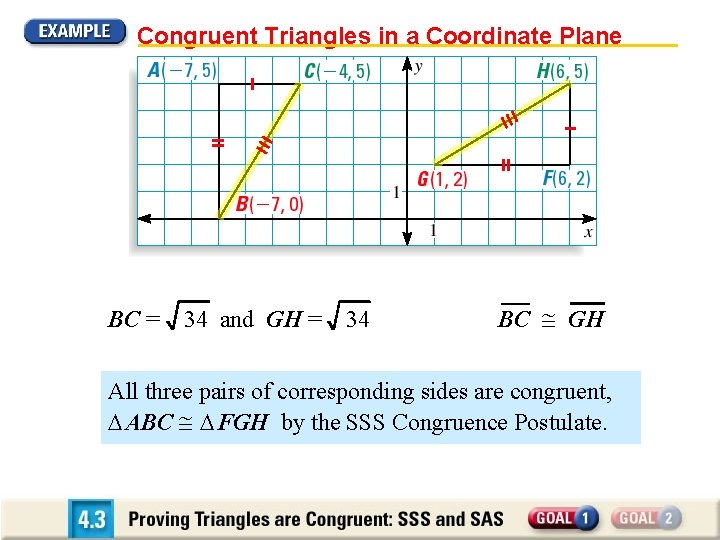
Congruent Triangles in a Coordinate Plane BC = 34 and GH = 34 BC GH All three pairs of corresponding sides are congruent, ABC FGH by the SSS Congruence Postulate.