Learning Target 1 I can define dilation 2





- Slides: 9

Learning Target 1. I can define dilation. 2. I can perform a dilation with a given center and scale factor on a figure in the coordinate plane.

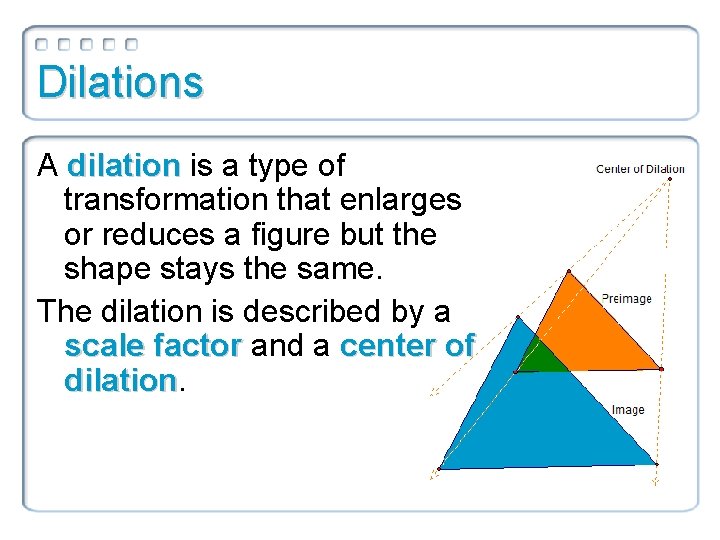
Dilations A dilation is a type of transformation that enlarges or reduces a figure but the shape stays the same. The dilation is described by a scale factor and a center of dilation

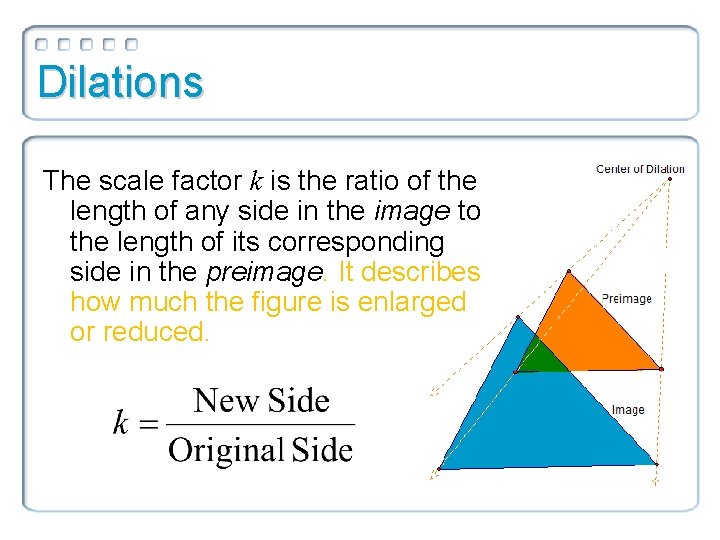
Dilations The scale factor k is the ratio of the length of any side in the image to the length of its corresponding side in the preimage. It describes how much the figure is enlarged or reduced.

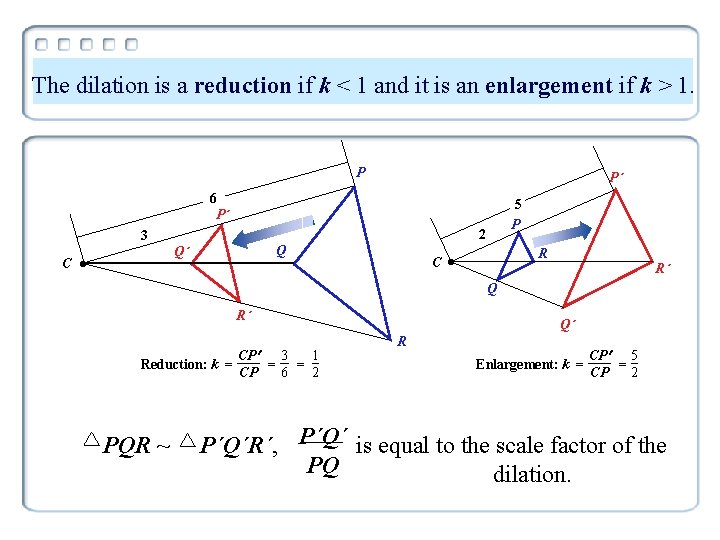
The dilation is a reduction if k < 1 and it is an enlargement if k > 1. P P´ 6 P´ 2 3 C Q Q´ • 5 P C R • R´ Q R´ Reduction: k = PQR ~ 3 CP 1 = = 6 CP 2 Q´ R Enlargement: k = CP 5 = CP 2 P´Q´R´, P´Q´ is equal to the scale factor of the PQ dilation.

Constructing a Dilation Examples of dilations of a triangle.

Questions/ Observations: Step 8: How do they compare to the original coordinates? P(x, y) P´(kx, ky) Pre-image A(3, 6) B(7, 6) C(7, 3) Image A´(9, 18) B´(21, 18) C´(21, 9)

In a coordinate plane, dilations whose centers are the origin have the property that the image of P(x, y) is P´(kx, ky). Draw a dilation of rectangle ABCD with A(2, 2), B(6, 2), C(6, 4), and D(2, 4). Use the origin as the center and use a scale factor of 1. How does the perimeter of the preimage compare to the perimeter of the image? 2 SOLUTION Because the center of the dilation is the origin, you can find the image of each vertex by multiplying its coordinates by the scale factor. A(2, 2) A´(1, 1) B(6, 2) B´(3, 1) C(6, 4) C ´(3, 2) D(2, 4) D´(1, 2) y D D´ A A´ 1 O • 1 C C´ B B´ x

In a coordinate plane, dilations whose centers are the origin have the property that the image of P(x, y) is P´(kx, ky). Draw a dilation of rectangle ABCD with A(2, 2), B(6, 2), C(6, 1 use a scale 4), and D(2, 4). Use the origin as the center and 2 factor of. How does the perimeter of the preimage compare to the perimeter of the image? SOLUTION From the graph, you can see that the preimage has a perimeter of 12 and the image has a perimeter of 6. A preimage and its image after a dilation are similar figures. Therefore, the ratio of the perimeters of a preimage and its image is equal to the scale factor of the dilation. y D D´ A A´ 1 O • 1 C C´ B B´ x

Example 3 Determine if ABCD and A’B’C’D’ are similar figures. If so, identify the scale factor of the dilation that maps ABCD onto A’B’C’D’ as well as the center of dilation. Is this a reduction or an enlargement?