Learning Objectives March 2021 To use Pythagoras Theorem

Learning Objectives: March 2021 • To use Pythagoras’ Theorem to find the longest side in a right-angled triangle. Starter Find the to answers to the following questions, use your calculator if needed. Copy each question and write answers to 1 d. p. where needed. 1) 92 2) 142 3) 202 4) 0. 72 5) 6) 9) 5. 382 10) 7) 8)

By the end of the lesson • All of you will recognise the Theorem of Pythagoras and be able to write it down. • Most of you will be able to use theorem to calculate the longest side in a right-angled triangle. [Level 7. 2] • Some of you will be able to use theorem to calculate one of the shorter sides of a right-angled triangle. [Level 7. 8]

The Theorem of Pythagoras was a Greek mathematician who summarised hundreds of years of knowledge about the properties of rightangled triangles. His rule focused on squares drawn on the sides of right-angled triangles. We are going to try to discover his rule or THEOREM. http: //www. ies. co. jp/math/java/geo/pytha 2. html Pythagoras of Samos (6 C BC) c b a

1. Cut out the small squares and then cut along the dotted lines of the one of the squares. 2. Try to fit these parts together on the large square. 3. Use the right angles to fit into the corners of the large square

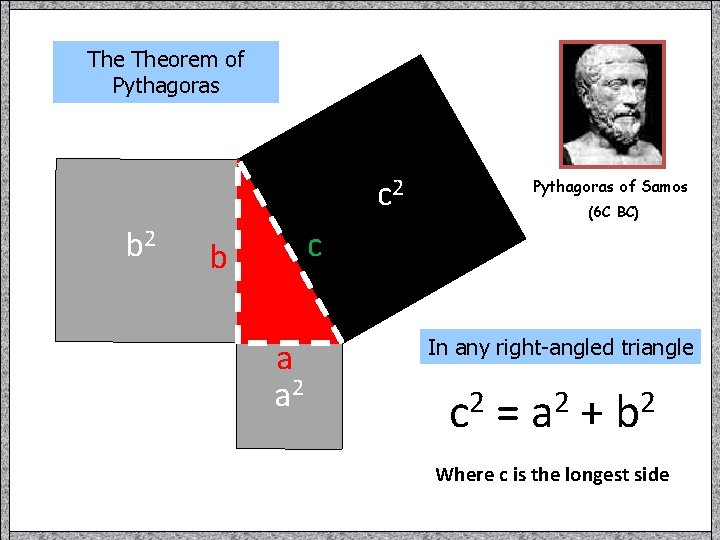
The Theorem of Pythagoras c 2 b 2 Pythagoras of Samos (6 C BC) c b a a 2 In any right-angled triangle c 2 = a 2 + b 2 Where c is the longest side

Using theorem of Pythagoras We can use theorem to find one missing side in a rightangled triangle A GOOD ANSWER SHOULD LOOK LIKE THIS 10 cm y c 2 = a 2 + b 2 The general theorem y 2 Substitute into the formula = 62 + 102 y 2 = 36 + 100 6 cm Work out the squares y 2 = 136 y= y = 11. 7 cm To calculate y find the square root Answer to 1 d. p.

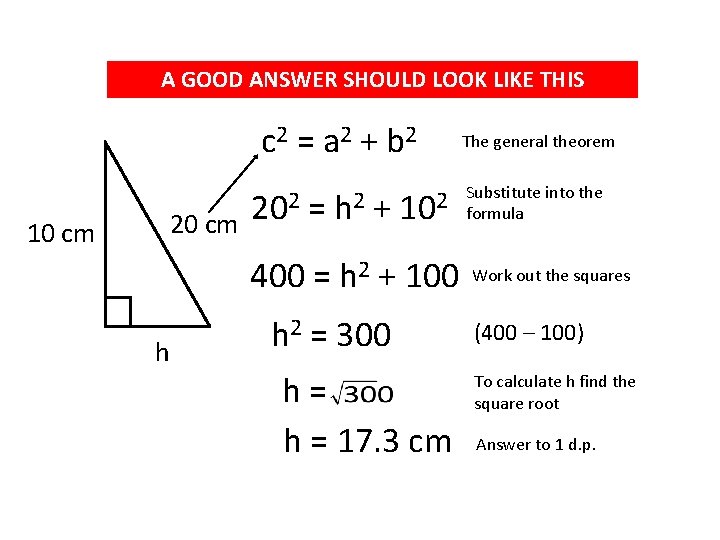
A GOOD ANSWER SHOULD LOOK LIKE THIS c 2 = a 2 + b 2 20 cm 10 cm 202 = h 2 + 102 400 = h 2 + 100 h h 2 = 300 h= h = 17. 3 cm The general theorem Substitute into the formula Work out the squares (400 – 100) To calculate h find the square root Answer to 1 d. p.

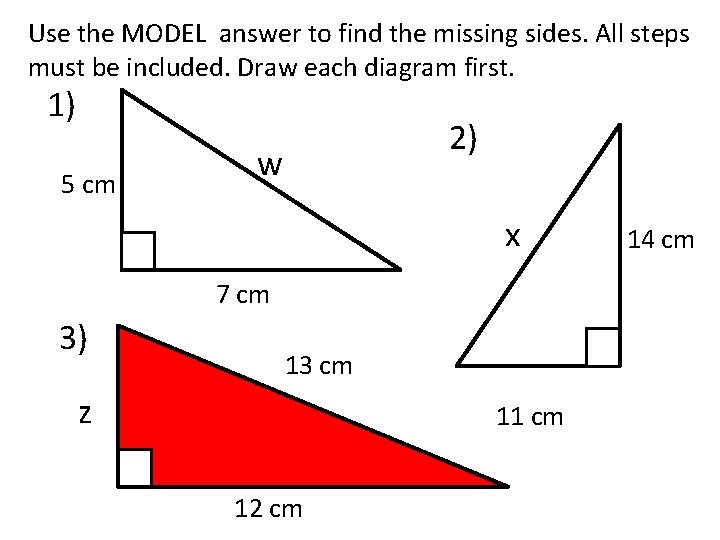
Use the MODEL answer to find the missing sides. All steps must be included. Draw each diagram first. 1) 5 cm 2) w x 7 cm 3) 13 cm z 11 cm 12 cm 14 cm

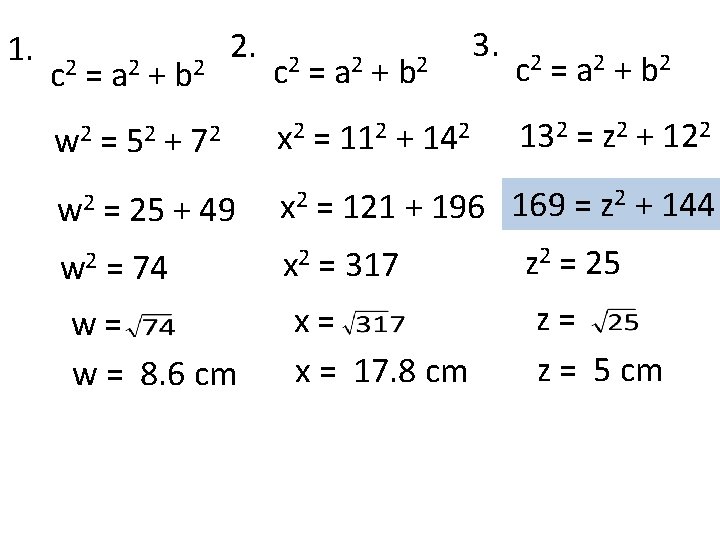
1. c 2 = w 2 w 2 a 2 = + 52 b 2 + 2. 72 c 2 = a 2 + b 2 x 2 = 112 + 142 3. c 2 = a 2 + b 2 132 = z 2 + 122 = 25 + 49 x 2 = 121 + 196 169 = z 2 + 144 = 74 x 2 = 317 w= w = 8. 6 cm x= x = 17. 8 cm z 2 = 25 z= z = 5 cm

By the end of the lesson • All of you will recognise the Theorem of Pythagoras and be able to write it down. • Most of you will be able to use theorem to calculate the longest side in a right-angled triangle. [Level 7. 2] • Some of you will be able to use theorem to calculate one of the shorter sides of a right-angled triangle. [Level 7. 8]