Learning Factors Analysis A General Method for Cognitive

Learning Factors Analysis – A General Method for Cognitive Model Evaluation and Improvement Hao Cen, Kenneth Koedinger, Brian Junker Human-Computer Interaction Institute Carnegie Mellon University

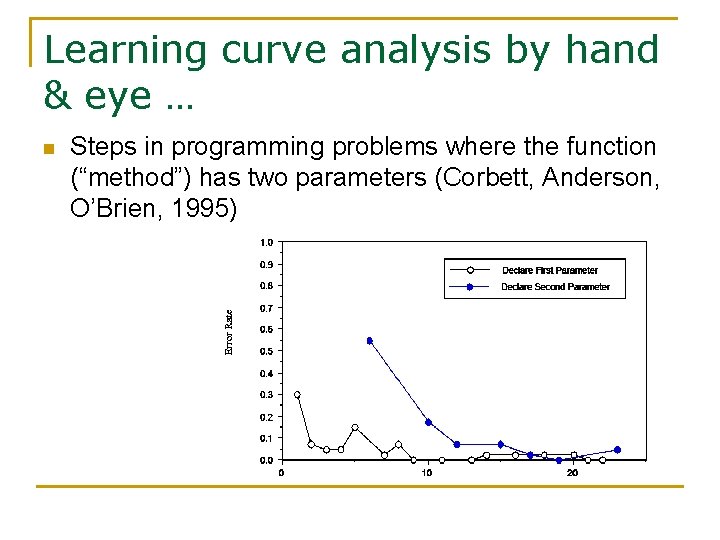
Learning curve analysis by hand & eye … n Steps in programming problems where the function (“method”) has two parameters (Corbett, Anderson, O’Brien, 1995)

Can learning curve analysis be automated? n Learning curve analysis q q q n Identify blips by hand & eye Manually create a new model Qualitative judgment Need to automatically: q q q Identify blips by system Propose alternative cognitive models Evaluate each model quantitatively

Overview n n n A Geometry Cognitive Model and Log Data Learning Factors Analysis algorithm Experiments and Results

Domain of current study n. Domain of study: the area unit of the geometry tutor n. Cognitive model: 15 skills 1. Circle-area 2. Circle-circumference 3. Circle-diameter 4. Circle-radius 5. Compose-by-addition 6. Compose-by-multiplication 7. Parallelogram-area 8. Parallelogram-side 9. Pentagon-area 10. Pentagon-side 11. Trapezoid-area 12. Trapezoid-base 13. Trapezoid-height 14. Triangle-area 15. Triangle-side

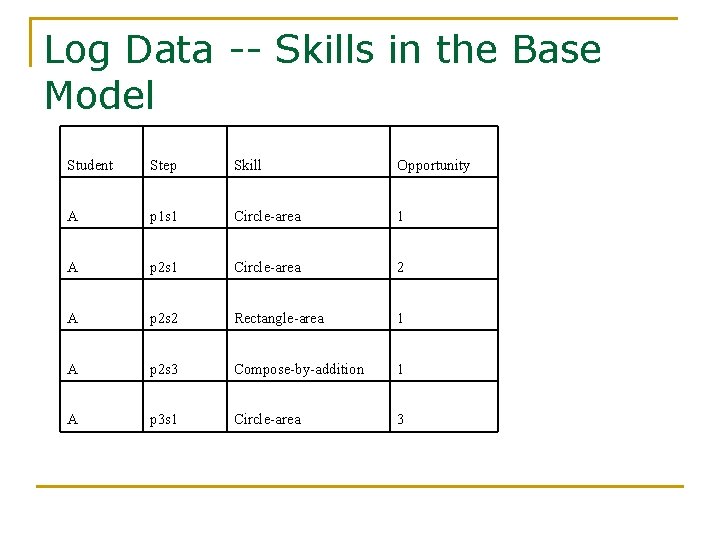
Log Data -- Skills in the Base Model Student Step Skill Opportunity A p 1 s 1 Circle-area 1 A p 2 s 1 Circle-area 2 A p 2 s 2 Rectangle-area 1 A p 2 s 3 Compose-by-addition 1 A p 3 s 1 Circle-area 3

Overview n n n Cognitive Models & Cognitive Tutors Literature Reviews on Model Improvement A Geometry Cognitive Model and Log Data Learning Factors Analysis algorithm Experiments and Results

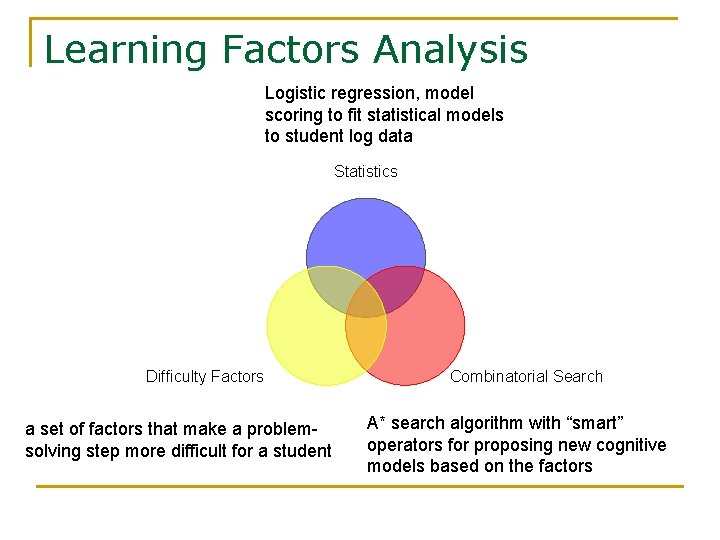
Learning Factors Analysis Logistic regression, model scoring to fit statistical models to student log data Statistics Difficulty Factors a set of factors that make a problemsolving step more difficult for a student Combinatorial Search A* search algorithm with “smart” operators for proposing new cognitive models based on the factors

The Statistical Model p Probability of getting a step correct (p) is proportional to: - - if student i performed this step = Xi, add overall “smarts” of that student = i if skill j is needed for this step = Yj, add easiness of that skill = j add product of number of opportunities to learn = Tj & amount gained for each opportunity = j Use logistic regression because response is discrete (correct or not) Probability (p) is transformed by “log odds” “stretched out” with “s curve” to not bump up against 0 or 1 (Related to “Item Response Theory”, behind standardized tests …)

Difficulty Factors n Difficulty Factors -- a property of the problem that causes student difficulties q n Like first vs. second parameter in LISP example above Four factors in this study q Embed: alone, embed q Backward: forward, backward q Repeat: initial, repeat q Figure. Part: area, area-difference, area-combination, diameter, circumference, radius, side, segment, base, height, apothem Embed factor: Whether figure is embedded in another figure or by itself (alone) Example for skill Circle Area: Q: Given AB = 2, find circle area in the context of the problem goal to calculate the shaded area A B

Goal: Do model selection within the logistic regression model space Combinatorial Search Steps: n 1. 2. 3. 4. Start from an initial “node” in search graph Iteratively create new child nodes by splitting a model using covariates or “factors” Employ a heuristic (e. g. fit to learning curve) to rank each node Expand from a new node in the heuristic order by going back to step 2

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

System: Best-first Search n n n an informed graph search algorithm guided by a heuristic Heurisitcs – AIC, BIC Start from an existing model

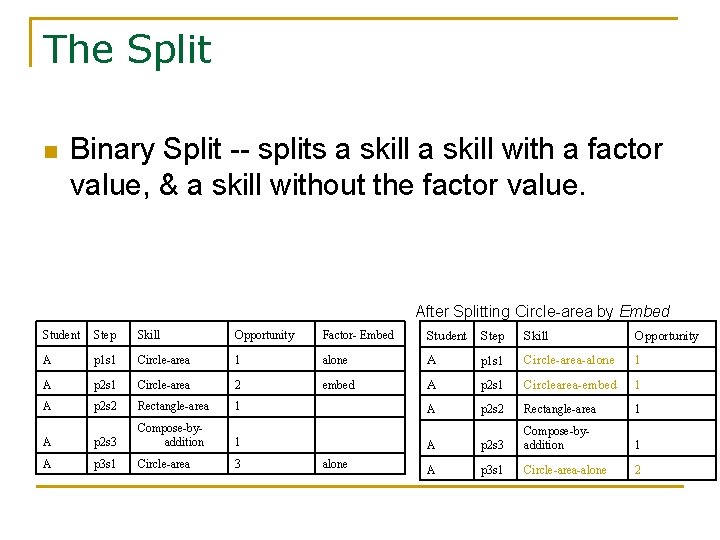
The Split n Binary Split -- splits a skill with a factor value, & a skill without the factor value. After Splitting Circle-area by Embed Student Step Skill Opportunity Factor- Embed Student Step Skill Opportunity A p 1 s 1 Circle-area 1 alone A p 1 s 1 Circle-area-alone 1 A p 2 s 1 Circle-area 2 embed A p 2 s 1 Circlearea-embed 1 A p 2 s 2 Rectangle-area 1 A p 2 s 3 Compose-byaddition 1 A p 3 s 1 Circle-area 3 A p 3 s 1 Circle-area-alone 2 alone

The Heuristics n Good model captures sufficient variation in data but is not overly complicated q n balance between model fit & complexity minimizing prediction risk (Wasserman 2005) AIC and BIC used as heuristics in the search q q q two estimators for prediction risk balance between fit & parisimony select models that fit well without being too complex AIC = -2*log-likelihood + 2*number of parameters BIC = -2*log-likelihood + number of parameters * number of observations

Overview n n n Cognitive Models & Cognitive Tutors Literature Reviews on Model Improvement A Geometry Cognitive Model and Log Data Learning Factors Analysis algorithm Experiments and Results

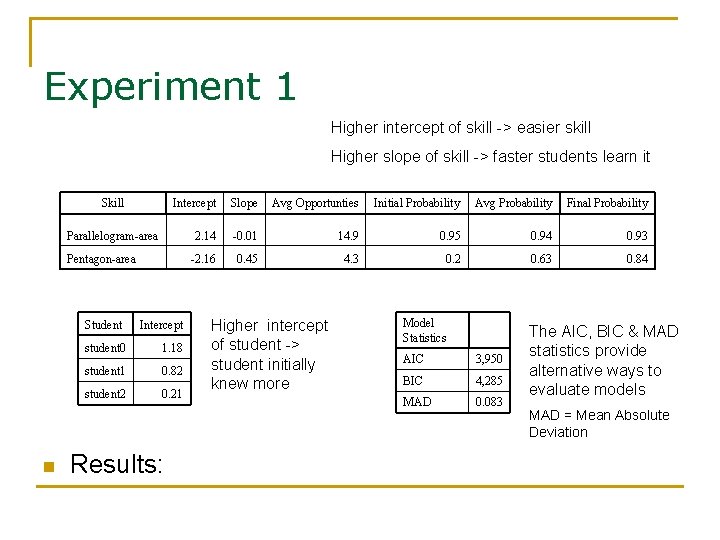
Experiment 1 n n Q: How can we describe learning behavior in terms of an existing cognitive model? A: Fit logistic regression model in equation above (slide 27) & get coefficients

Experiment 1 Higher intercept of skill -> easier skill Higher slope of skill -> faster students learn it Skill Intercept Slope Avg Opportunties Initial Probability Avg Probability Final Probability 2. 14 -0. 01 14. 9 0. 95 0. 94 0. 93 -2. 16 0. 45 4. 3 0. 2 0. 63 0. 84 Parallelogram-area Pentagon-area Student n Intercept student 0 1. 18 student 1 0. 82 student 2 0. 21 Results: Higher intercept of student -> student initially knew more Model Statistics AIC 3, 950 BIC 4, 285 MAD 0. 083 The AIC, BIC & MAD statistics provide alternative ways to evaluate models MAD = Mean Absolute Deviation

Experiment 2 n n Q: How can we improve a cognitive model? A: Run LFA on data including factors & search through model space

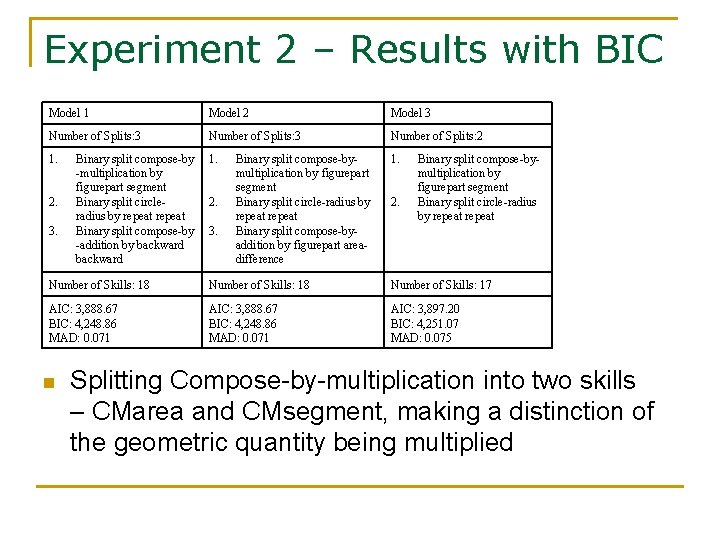
Experiment 2 – Results with BIC Model 1 Model 2 Model 3 Number of Splits: 2 1. 1. 2. 3. Binary split compose-by -multiplication by figurepart segment Binary split circleradius by repeat Binary split compose-by -addition by backward 2. 3. Binary split compose-bymultiplication by figurepart segment Binary split circle-radius by repeat Binary split compose-byaddition by figurepart areadifference 2. Binary split compose-bymultiplication by figurepart segment Binary split circle-radius by repeat Number of Skills: 18 Number of Skills: 17 AIC: 3, 888. 67 BIC: 4, 248. 86 MAD: 0. 071 AIC: 3, 897. 20 BIC: 4, 251. 07 MAD: 0. 075 n Splitting Compose-by-multiplication into two skills – CMarea and CMsegment, making a distinction of the geometric quantity being multiplied

Experiment 3 n n Q: Will some skills be better merged than if they are separate skills? Can LFA recover some elements of original model if we search from a merged model, given difficulty factors? A: Run LFA on the data of a merged model, and search through the model space

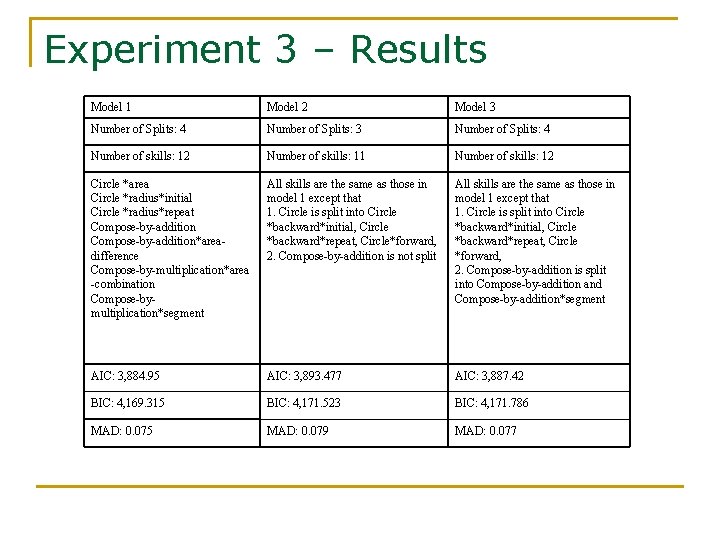
Experiment 3 – Merged Model n Merge some skills in the original model to remove some distinctions, add as a difficulty factors to consider n The merged model has 8 skills: q q q q n Circle-area, Circle-radius => Circle-circumference, Circle-diameter => Circle-CD Parallelogram-area and Parallelogram-side => Parallelogram Pentagon-area, Pentagon-side => Pentagon Trapezoid-area, Trapezoid-base, Trapezoid-height => Trapezoid Triangle -area, Triangle -side => Triangle Compose-by-addition Compose-by-multiplication Add difficulty factor “direction”: forward vs. backward

Experiment 3 – Results Model 1 Model 2 Model 3 Number of Splits: 4 Number of Splits: 3 Number of Splits: 4 Number of skills: 12 Number of skills: 11 Number of skills: 12 Circle *area Circle *radius*initial Circle *radius*repeat Compose-by-addition*areadifference Compose-by-multiplication*area -combination Compose-bymultiplication*segment All skills are the same as those in model 1 except that 1. Circle is split into Circle *backward*initial, Circle *backward*repeat, Circle*forward, 2. Compose-by-addition is not split All skills are the same as those in model 1 except that 1. Circle is split into Circle *backward*initial, Circle *backward*repeat, Circle *forward, 2. Compose-by-addition is split into Compose-by-addition and Compose-by-addition*segment AIC: 3, 884. 95 AIC: 3, 893. 477 AIC: 3, 887. 42 BIC: 4, 169. 315 BIC: 4, 171. 523 BIC: 4, 171. 786 MAD: 0. 075 MAD: 0. 079 MAD: 0. 077

Experiment 3 – Results n n Recovered three skills (Circle, Parallelogram, Triangle) => distinctions made in the original model are necessary Partially recovered two skills (Triangle, Trapezoid) => some original distinctions necessary, some are not Did not recover one skill (Circle-CD) => original distinction may not be necessary Recovered one skill (Pentagon) in a different way => Original distinction may not be as significant as distinction caused by another factor

Beyond Experiments 1 -3 n Q: Can we use LFA to improve tutor curriculum by identifying over-taught or under -taught rules? q n Thus adjust their contribution to curriculum length without compromising student performance A: Combine results from experiments 1 -3

Beyond Experiments 1 -3 -Results n Parallelogram-side is over taught. q q n Trapezoid-height is under taught. q q n high intercept (2. 06), low slope (-. 01). initial success probability. 94, average number of practices per student is 15 low intercept (-1. 55), positive slope (. 27). final success probability is. 69, far away from the level of mastery, the average number of practices per student is 4. Suggestions for curriculum improvement q q Reducing the amount of practice for Parallelogram-side should save student time without compromising their performance. More practice on Trapezoid-height is needed for students to reach mastery.

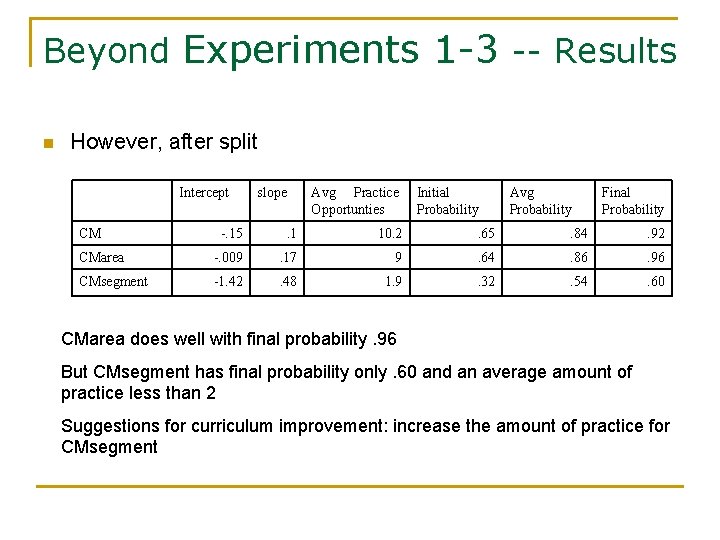
Beyond Experiments 1 -3 -Results n How about Compose-by-multiplication? Intercept CM -. 15 slope Avg Practice Opportunties . 1 10. 2 Initial Probability. 65 Avg Probability Final Probability . 84 . 92 With final probability. 92 students seem to have mastered Compose-by-multiplication.

Beyond Experiments 1 -3 -- Results n However, after split Intercept CM slope Avg Practice Opportunties Initial Probability Avg Probability Final Probability -. 15 . 1 10. 2 . 65 . 84 . 92 CMarea -. 009 . 17 9 . 64 . 86 . 96 CMsegment -1. 42 . 48 1. 9 . 32 . 54 . 60 CMarea does well with final probability. 96 But CMsegment has final probability only. 60 and an average amount of practice less than 2 Suggestions for curriculum improvement: increase the amount of practice for CMsegment

Conclusions and Future Work n n Learning Factors Analysis combines statistics, human expertise, & combinatorial search to evaluate & improve a cognitive model System able to evaluate a model in seconds & search 100 s of models in 4 -5 hours q q n Model statistics are meaningful Improved models are interpretable & suggest tutor improvement Planning to use LFA for datasets from other tutors to test potential for model & tutor improvement

Acknowledgements n This research is sponsored by a National Science Foundation grant to the Pittsburgh Science of Learning Center. We thank Joseph Beck, Albert Colbert, and Ruth Wylie for their comments.

END

To do n Reduce DFA-LFA. ppt, get from ERM lecture q q n Go over 2 nd exercise on creating learning curves (from web site) in this talk & finish in 2 nd session? Print paper …. Other q Mail LOI feedback to Bett, add Kurt’s refs