Learning factor graphs in polynomial time sample complexity

Learning factor graphs in polynomial time & sample complexity Pieter Abbeel Daphne Koller Andrew Y. Ng Stanford University

Overview n First polynomial time & sample complexity learning algorithm for factor graphs, n n a superset of Bayesian nets, Markov nets. Applicable to any factor graph of bounded factor size and connectivity, n n Introduction including intractable networks (e. g. , grids). New technical ideas: n n Parameter learning: closed-form; parameterization with low-dimensional frequencies only. Structure learning: results about guaranteedapproximate Markov blankets from sample data. 1

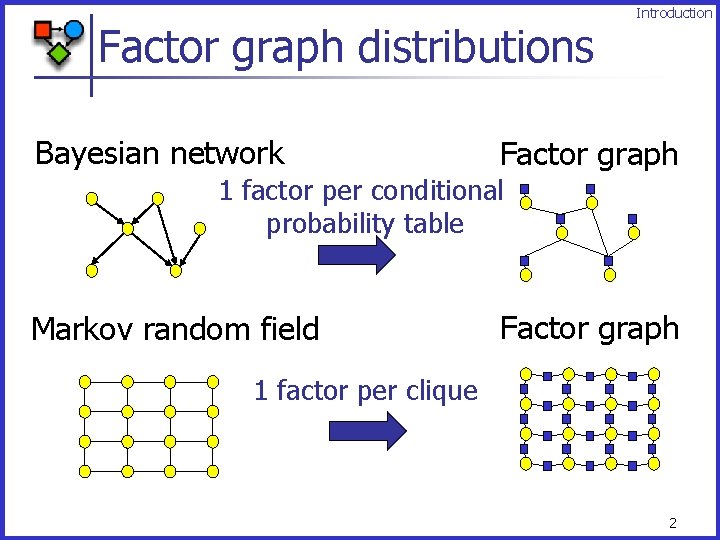
Factor graph distributions Bayesian network Introduction Factor graph 1 factor per conditional probability table Markov random field Factor graph 1 factor per clique 2

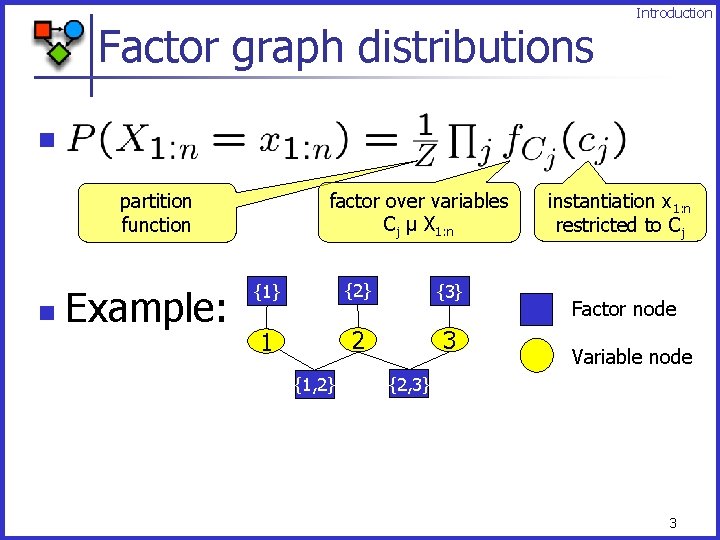
Factor graph distributions n … factor over variables Cj µ X 1: n partition function n Introduction Example: {1} {2} {3} 1 2 3 {1, 2} instantiation x 1: n restricted to Cj Factor node Variable node {2, 3} 3

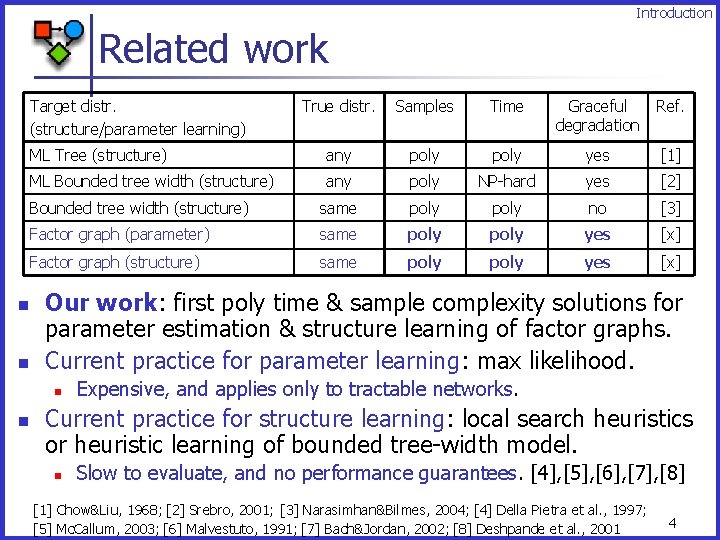
Introduction Related work Target distr. (structure/parameter learning) n n True distr. Samples Time Graceful degradation Ref. ML Tree (structure) any poly yes [1] ML Bounded tree width (structure) any poly NP-hard yes [2] Bounded tree width (structure) same poly no [3] Factor graph (parameter) same poly yes [x] Factor graph (structure) same poly yes [x] Our work: first poly time & sample complexity solutions for parameter estimation & structure learning of factor graphs. Current practice for parameter learning: max likelihood. n n Expensive, and applies only to tractable networks. Current practice for structure learning: local search heuristics or heuristic learning of bounded tree-width model. n Slow to evaluate, and no performance guarantees. [4], [5], [6], [7], [8] [1] Chow&Liu, 1968; [2] Srebro, 2001; [3] Narasimhan&Bilmes, 2004; [4] Della Pietra et al. , 1997; [5] Mc. Callum, 2003; [6] Malvestuto, 1991; [7] Bach&Jordan, 2002; [8] Deshpande et al. , 2001 4

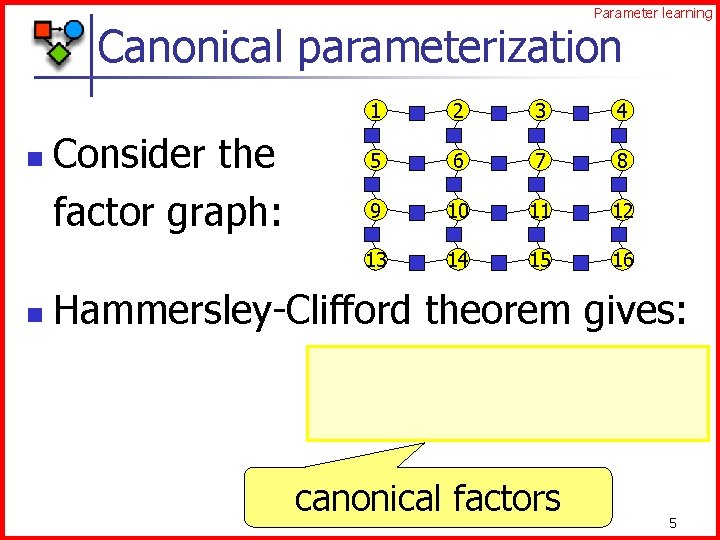
Parameter learning Canonical parameterization n n Consider the factor graph: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 Hammersley-Clifford theorem gives: canonical factors 5

Canonical factors n Parameter learning No lower-order interactions by inclusion-exclusion: Complete interaction. Subtract lower order interactions. Compensate for double counting. Frequencies only. Equal # of +, - terms. Closed-form parameter learning ? NO. (Not yet. ) The frequencies P(X 1: 16=(x 1, x 2, 0, …, 0)) involve full instantiations and are thus expensive to estimate from samples. 6

Parameter learning Markov blanket canonical factors Positive and negative term of canonical factor: Transform to conditional probability. Terms cancel. Conditional independence. Low dimensional distributions. (MB: Markov blanket. ) 7

Parameter learning Markov blanket canonical factors n n {Cj*}: all subfactors of the given structure. : from distribution over Cj*, MB(Cj*). • Low dimensional distributions. • Efficient estimation from samples. n Example: 8

Parameter learning n Algorithm: n n n Parameter learning Estimate the Markov blanket canonical factors from data. Return Theorem. The parameter learning algorithm n n runs in polynomial time, uses polynomial # of samples, guarantees: D(……) is small with high probability. No dependence on tree-width of the network! 9

Graceful degradation n Parameter learning Theorem. When true distribution: factor graph G, structure for parameter learning: factor graph G ( G), n n the additional error consists of two terms: Canonical factors capture residual highest-order interactions only. Small error when subfactors are in G. MB in given factor graph G If MB is a good approximation of MB, error will be small. (See structure learning. ) 10

Structure learning n Assume factor size k. Structure: all factors of size k NO: Parameter + learning = ? Structure learning Estimating Markov blanket canonical factors requires knowledge of the Markov blankets. But if we knew the Markov blankets, structure learning problem would be solved. 11

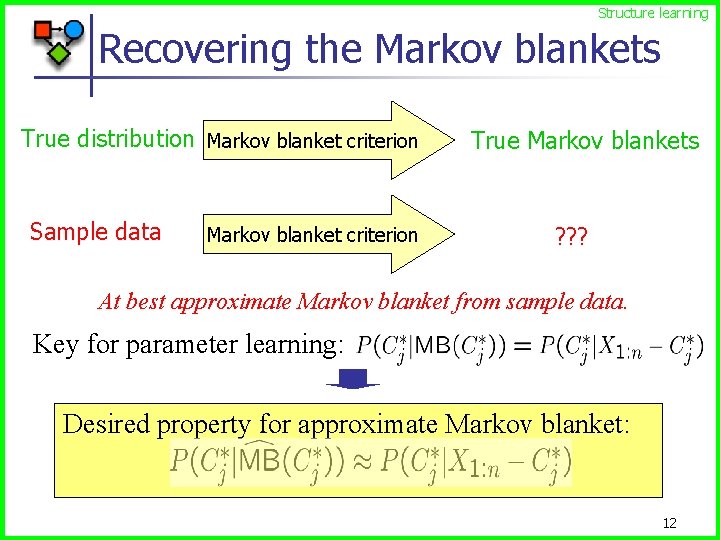
Structure learning Recovering the Markov blankets True distribution Markov blanket criterion Sample data Markov blanket criterion True Markov blankets ? ? ? At best approximate Markov blanket from sample data. Key for parameter learning: Desired property for approximate Markov blanket: 12

Structure learning Conditional entropy n Conditional entropy: n For any candidate Markov blanket Y : Conditional independence Thus What about Conditioning reduces entropy: For any X, Y, Z H (X |Y, Z ) H (X |Y ). True distribution Conditional entropy Sample data Conditional entropy True Markov blankets ? ? ? 13

Structure learning Conditional entropy Theorem. Conditional entropy satisfies the desired approximate Markov blanket property: MB(C) looks like For any > 0, Markov blanket if n Theorem. Empirical conditional entropy estimates are a good approximation for the true conditional entropy, even with poly number of samples. n then where MB(C) can be used as Markov blanket for learning 14

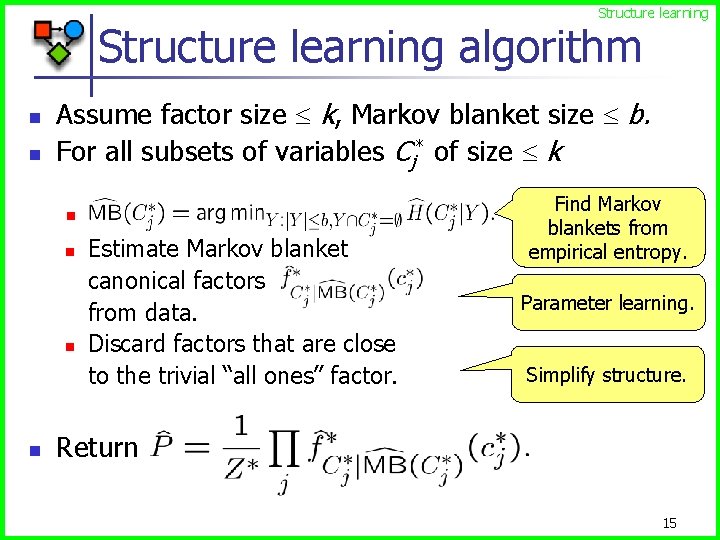
Structure learning algorithm n n Assume factor size k, Markov blanket size b. For all subsets of variables Cj* of size k n n n Estimate Markov blanket canonical factors from data. Discard factors that are close to the trivial “all ones” factor. Find Markov blankets from empirical entropy. Parameter learning. Simplify structure. Return 15

Structure learning theorem n n Assume fixed: factor size k, MB size b. Theorem. The structure learning algorithm n n n runs in polynomial time, uses polynomial # of samples, guarantees: D(……) is small with high probability. Note: n n Exponential dependence on factor size, MB size for computational and sample complexity. Bounded connectivity implies bounded factor and MB size. No dependence on tree-width of the network! 16

Graceful degradation Theorem. Let G be the factor graph of true distribution. When in the true distribution the max factor size > k or max MB size > b, the additional error consists of three terms: Canonical factors capture residual highest-order interactions only. Small error when small true interactions of order > k. n Structure learning If MB is a good approximation of MB, error will be small. Factors that are trivial in the true distribution; but estimated as nontrivial since their MB size is larger than b. 17

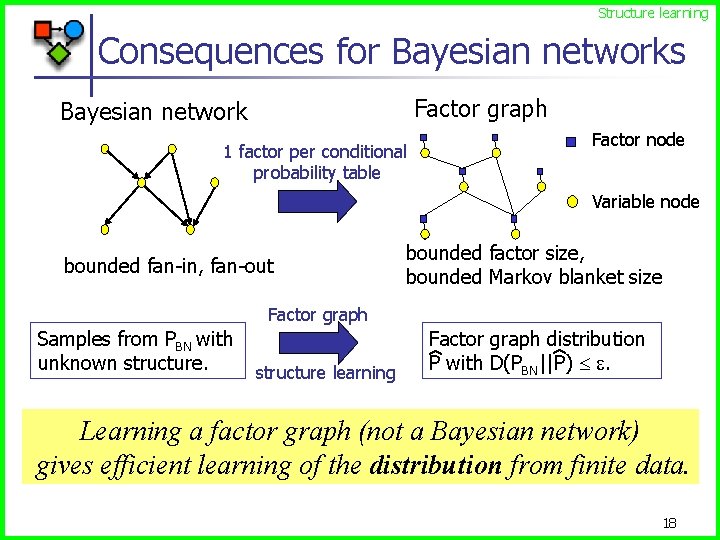
Structure learning Consequences for Bayesian networks Factor graph Bayesian network Factor node 1 factor per conditional probability table Variable node bounded fan-in, fan-out bounded factor size, bounded Markov blanket size Factor graph structure learning Factor graph distribution P with D(PBN||P) . Samples from PBN with unknown structure. Learning a factor graph (not a Bayesian network) gives efficient learning of the distribution from finite data. 18

Related work n Finding highest scoring, bounded in-degree Bayesian network is NP-hard (Chickering, Meek & Heckerman, 2003). ? n n Structure learning n n Our algorithm recovers a factor graph representation only. The (difficult) acyclicity constraint is avoided. Learning a factor graph (not a Bayesian network) gives efficient learning of the distribution from finite data. Note: Spirtes, Glymour & Scheines (2000) and Chickering & Meek (2002) do recover Bayesian network structure, but only with access to true distribution (infinite sample size). 19

Discussion and conclusion n n First polynomial time & polynomial sample complexity learning algorithm for factor graphs. Applicable to any factor graph of bounded factor size and connectivity, n n Conclusion including intractable networks (e. g. , grids). Practical drawbacks of the proposed algorithm: n n n Estimates parameters from only small fraction of data. Structure learning: algorithm enumerates all possible Markov blankets. Complexity exponential in Markov blanket size. 20

Done. . . n Additional and outdated slides follow. 21

Detailed theorem statements Parameter learning theorem 22

Detailed theorem statements Structure learning theorem 23

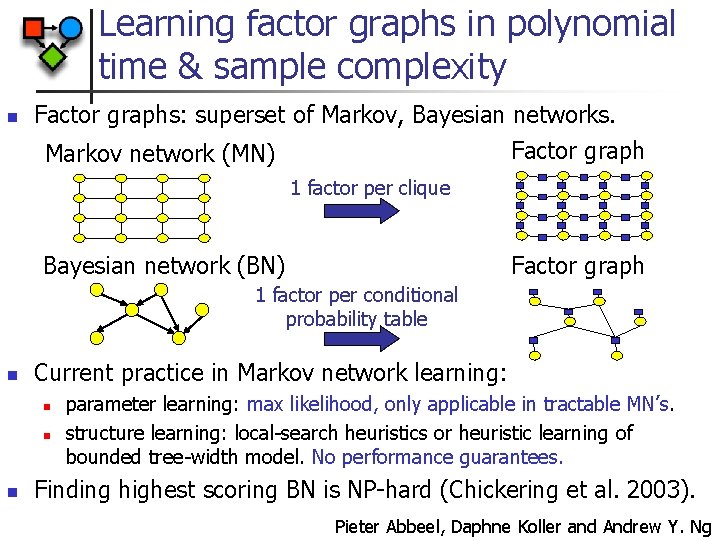
Learning factor graphs in polynomial time & sample complexity n Factor graphs: superset of Markov, Bayesian networks. Factor graph Markov network (MN) 1 factor per clique Bayesian network (BN) Factor graph 1 factor per conditional probability table n Current practice in Markov network learning: n n n parameter learning: max likelihood, only applicable in tractable MN’s. structure learning: local-search heuristics or heuristic learning of bounded tree-width model. No performance guarantees. Finding highest scoring BN is NP-hard (Chickering et al. 2003). Pieter Abbeel, Daphne Koller and Andrew Y. Ng

Learning factor graphs in polynomial time & sample complexity n n First polynomial time & sample complexity learning algorithm for factor graphs. Applicable to any factor graph of bounded factor size and connectivity, n n including intractable networks (e. g. , grids). New technical ideas: n n Parameter learning: in closed-form, using parameterization with low-dimensional frequencies only. Structure learning: results about guaranteedapproximate Markov blankets from sample data. Pieter Abbeel, Daphne Koller and Andrew Y. Ng

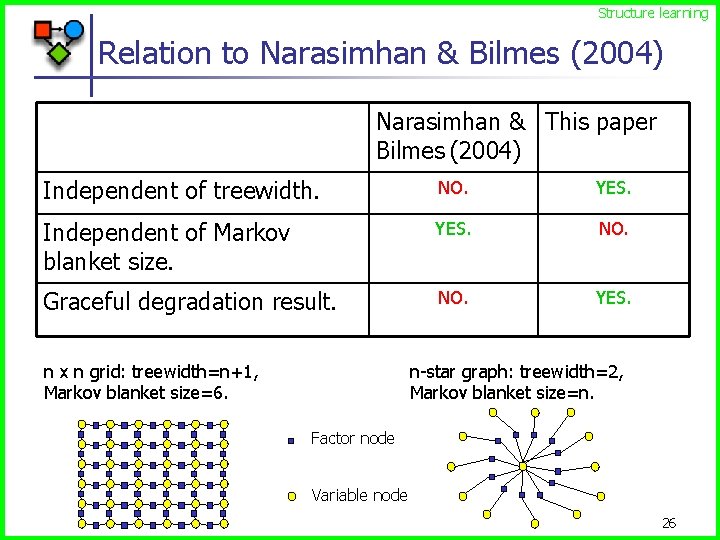
Structure learning Relation to Narasimhan & Bilmes (2004) Narasimhan & This paper Bilmes (2004) Independent of treewidth. NO. YES. Independent of Markov blanket size. YES. NO. Graceful degradation result. NO. YES. n x n grid: treewidth=n+1, Markov blanket size=6. n-star graph: treewidth=2, Markov blanket size=n. Factor node Variable node 26

Canonical parameterization 27

Canonical parameterization (2) 28

Canonical parameterization (3) 29

Markov blanket canonical factors 30

Markov blanket canonical parameterization 31

Approximate Markov blankets 32

Structure learning algorithm 33

Structure learning algorithm 34