Learning Document Type Definition from a set of

Learning Document Type Definition from a set of XML Documents Mr. Phanom Slisatkorn CSA 998556 15 Nov 2000

Outline n n n n Introduction & Statement of the Problem Objective & Scope of the Study Drawbacks of Related Works Methodology Implementation Experiments and Results Conclusion & Future work References

Introduction & Statement of problems n n n DTD provide way to validate the structure and content of XML documents as well as the effective storage and query. DTD is not compulsory and have some complications to create it from scratch. Traditional approaches for learning DTD trend to over generalization and fail to infer concise meaningful DTD.

Objective & Scope n n n To analyze the drawbacks of existing approaches. To propose heuristic machine learning approach by using the star height information for precisely inferring meta characters and enabling regular expression pattern detection. The scope of study will only emphasize on the construction of content model, which is challenging from the aspect of machine learning.

Drawbacks of Related Works n n n n SAXON DTD Generator Fred DTD Engine Data Descriptor by Example (DDb. E) XTRACT System

Drawbacks n Since String pattern matching is used in Generalization module. It doesn’t really understand regular expression pattern. (a(bc)+)+ = abcbcbcabc = a(bc)*abc n It doesn’t precise infer ? , +, * meta character. Repetitive token are fixed generalize to + in DDb. E and * in XTRACT. n

Drawbacks Over-generalization problem e. g. (aa)+(bbb)+ -> aabbb, aabbbbbb It will be infer as -> a+b+ or a*b* n n Efficiency problem XTRACT generates many possible candidates from various parameter values so it produce large search space and need to use sophisticated algorithms to select candidates. aaaabbb -> a*b*, a*bbb, (aa)*b*

Contribution of Our approach (precisely infer ? , +, * and enable pattern detection between examples) (aa)+(bbb)+ ={aabbb, aaaabbb, Initialize Star Pattern aabbbbbb} -> a 2 b 3, a 4 b 3, a 2 b 6 Factoring -> a 2|4|2 b 3|3|6 Reduction& Generalization -> -> (aa)1|2|1(bbb)1|1|2 (aa)+(bbb)+

Contribution of Our approach (understand regular expression pattern) Initialize Star Pattern Factoring Reduction& Generalization (a(bc)+)+={abcbcbcabc} -> a(bc)3 a(bc)2 abc -> a(bc)3 a(bc)2 a (bc)1 -> (a(bc)3, 2, 1)3 -> unchanged -> (a(bc)+)+

Initial Star Pattern n Initialize Star Height Set Covering Problem Intra-Or Generalization(option)

Initialize Star Height e. g. abcbcbcabc a(bc)*abc, 3()2() a(bc)*a(bc)* , 3()2()1() (a(bc)*)* 3(3()2()1()) -> (a(bc)3, 2, 1)3 n Do n n Rule 1: if match(pattern, input) then f = f+1 Rule 2: elseif match(pattern, converse(input)) then f = f+1 Until cannot apply any rule Output pattern, f(star-height)

Regular expression pattern Converter(By unfolding[Bra 95]) Pattern Input string a(bc)*, abc, (bc)*, bc(bc)*, 1() bc, (bc)*, 1() , Remainder Output a(bc)* 1()

Set covering algorithm I = {abc, bcabc, abcbcbc, aabcaaabcbc}. P = {abc, bcabc, a(bc)3, (a 2, 3, 0 bc)3 } + Pattern. Guide Maximum |patternk| |Parsable Input sequences| Select (a*bc)* as general pattern then reform others Output={(a 1 bc)1, (a 0, 1 bc)2, (a 1, 0, 0 bc)3, (a 2, 3, 0 bc)3}

Intra-Or Generalization n n After keen star generalization if the input still contain the repetitions of the elements in any subsequence, those inputs potentially contain (a|b|. . )* patterns. Define the smallest scope by restriction that no other occurrence of elements inside the scope at outside. a, b, c, a*, c, d, e, f, g, e -> (a|b|c)*, d, (e|f|g)*

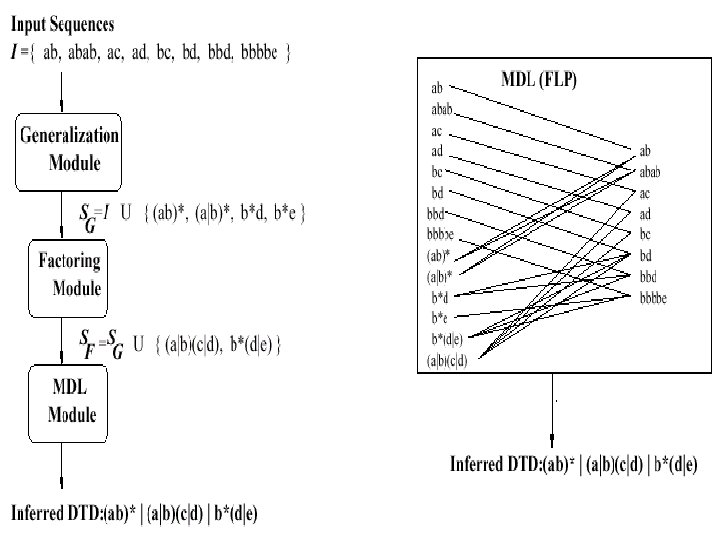
Factoring n Factors common sub expressions in order to produce more concise expression. We use a simplify version of factoring algorithm in XTRACT. n n I = {ac, ad, bc, bd} Output = (a|b)(c|d)

Reduction & Generalization n Remove Extraneous Parentheses ((a, b, c, ((d, (e)), f)), ((g|h)*) -> (a, b, c, d, e, f), (g|h)* (a, b, c, (d, e), f) -> (a, b, c, d, e, f) (a|b|c|(d|e)|f) -> (a|b|c|d|e|f) n Sort Or Element ((b|a|c)|e|d*|(a|b)|(f|e|d)) -> ((a|b)|(a|b|c)|d*|e|(d|e|f)) n Inter-Or Pattern Generalization (a*|e*|(ef*)|f*|(f(e|f))|g*) -> (a*|(e|f)*|g*)

Reduction & Generalization n Gcd generalization a 2|4|2 b 3|3|6 -> (aa)1|2|1(bbb)1|1|2 n Meta-characters generalization an=0|n=1 -> a? an>=1 -> a+ an=0|n>=1 -> a*

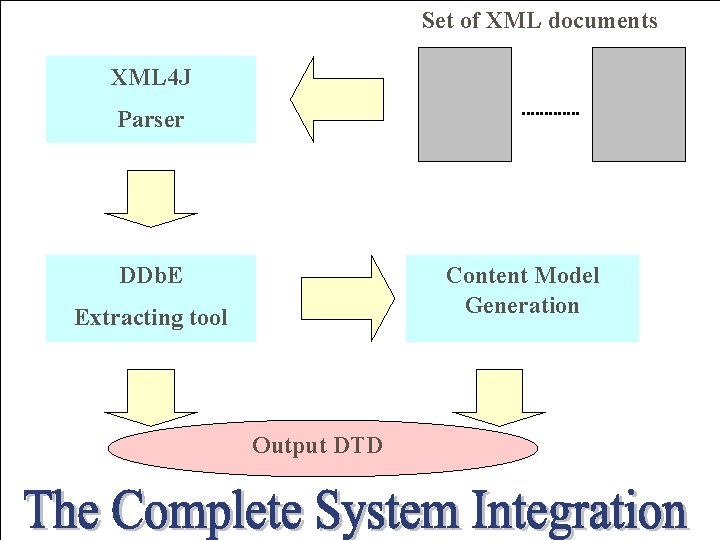
Set of XML documents XML 4 J Parser DDb. E Content Model Generation Extracting tool Output DTD

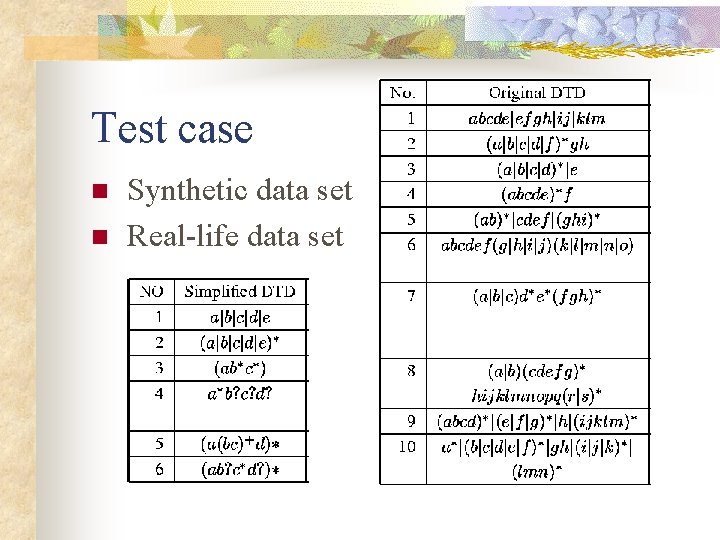
Experiment & Result n Experiment 1: (DDb. E) n n To demonstrate with a large distinct of XML instances, 1, 000 of XML documents are generated for each synthetic and real life DTD. Experiment 2: (DDb. E, SAXON and Fred) n We generate only 10 XML instances for each complex and cyclic DTD to demonstrate that our system requires only a small amount of examples for inferring a quality DTD.

Test case n n Synthetic data set Real-life data set

Conclusion & Future work n By introducing the star height information into learning process. n Precisely infer ? , +, * and enable pattern detection between examples n Enable regular expression pattern detection n Produce more precise and concise meaningful content model than other approaches. n By extend the pattern guide for covering all DTD structures It will provide personalization version of the standard DTD that more suitable to the user document sets.

References n n [Ang 96] Dana Angluin, A 1996 Snapshot of Computational Learning Theory, ACM Computing Surveys, 1996. [Bra 93] Brazma, A. , Efficient Identification of Regular Expression from Representative Examples, ACM COLT’ 93, 1993. [Bra 95] Brazma, A. , Learning of Regular Expressions by Pattern Matching. In Proceedings of the Computational Learning Theory, Euro. COLT’ 95: 392 -403, 1995. [Wan 89] A. R. R. Wang. Algorithms for Multi-level Logic Optimization. Ph. D thesis, The University of California, Berkeley, 1989.

Input sequences ={aabbb, aabbbbbb} Initialize Star Pattern -> a 2 b 3, a 4 b 3, a 2 b 6 Factoring -> a 2|4|2 b 3|3|6 Reduction& Generalization -> -> (aa)1|2|1(bbb)1|1|2 (aa)+(bbb)+