Learning Bayesian Networks Dimensions of Learning Model Bayes

Learning Bayesian Networks

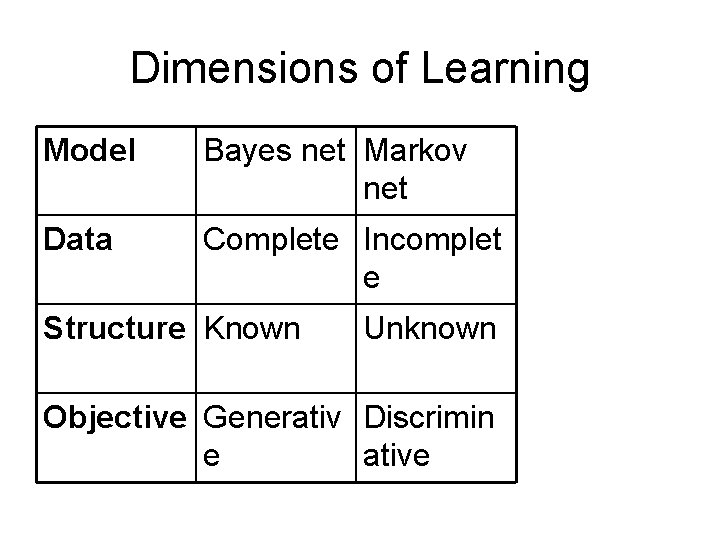
Dimensions of Learning Model Bayes net Markov net Data Complete Incomplet e Structure Known Unknown Objective Generativ Discrimin e ative

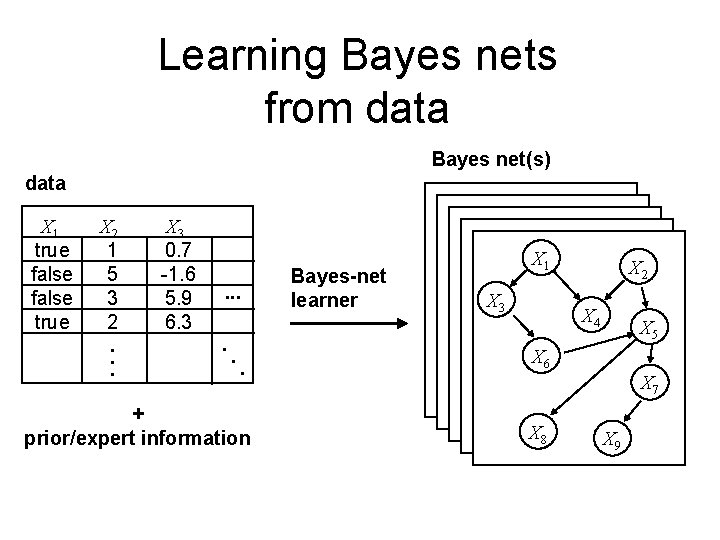
Learning Bayes nets from data Bayes net(s) data X 1 true false true X 2 1 5 3 2. . . X 3 0. 7 -1. 6 5. 9 6. 3 . . . Bayes-net learner X 1 X 3 X 2 X 4 . X 6 + prior/expert information X 8 X 5 X 7 X 9

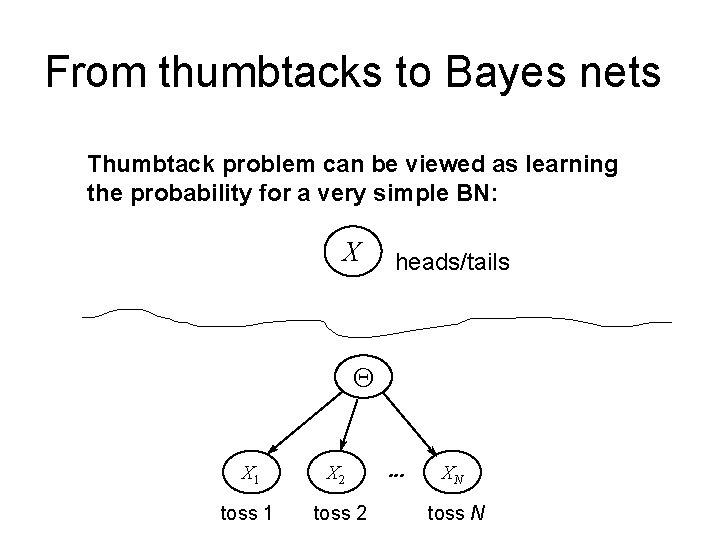
From thumbtacks to Bayes nets Thumbtack problem can be viewed as learning the probability for a very simple BN: X heads/tails Q X 1 X 2 toss 1 toss 2 . . . XN toss N

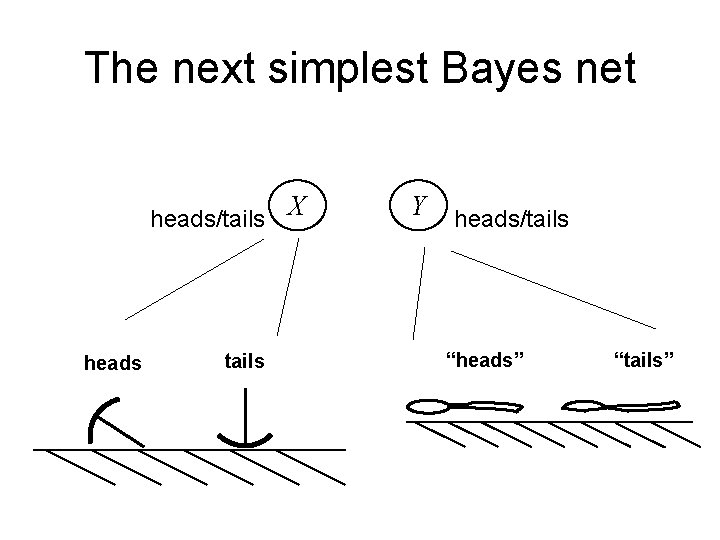
The next simplest Bayes net heads/tails X heads tails Y heads/tails “heads” “tails”

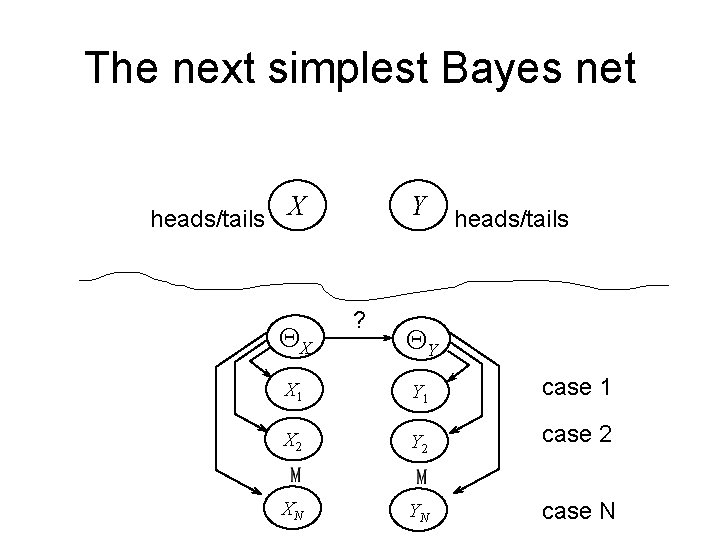
The next simplest Bayes net heads/tails X QX Y ? heads/tails QY X 1 Y 1 case 1 X 2 Y 2 case 2 XN YN case N

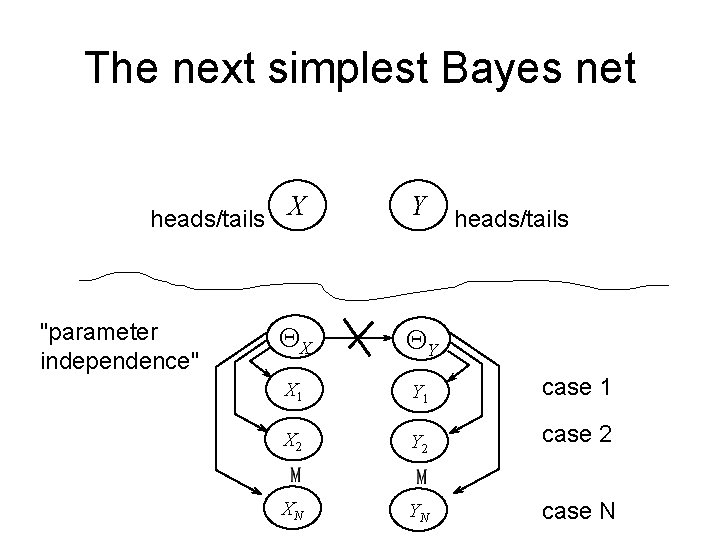
The next simplest Bayes net heads/tails X "parameter independence" Y heads/tails QX QY X 1 Y 1 case 1 X 2 Y 2 case 2 XN YN case N

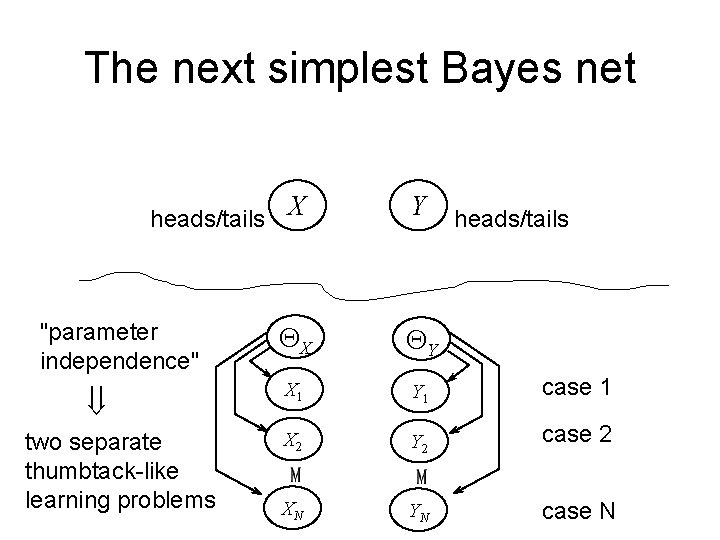
The next simplest Bayes net heads/tails X "parameter independence" ß two separate thumbtack-like learning problems Y heads/tails QX QY X 1 Y 1 case 1 X 2 Y 2 case 2 XN YN case N

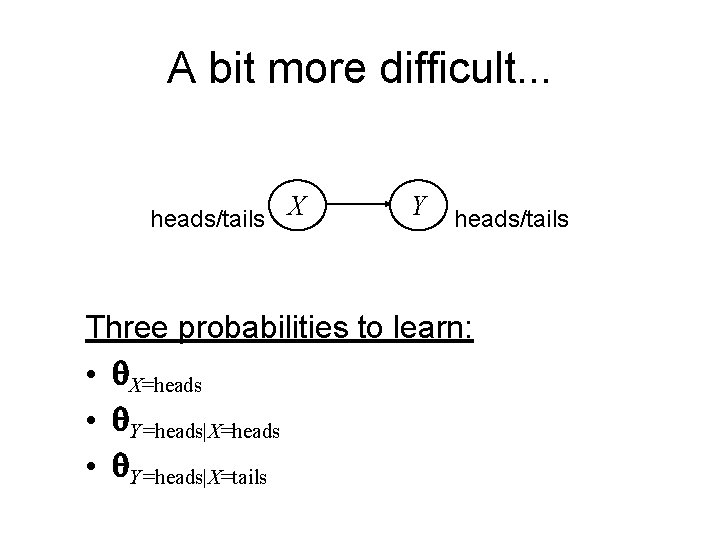
A bit more difficult. . . heads/tails X Y heads/tails Three probabilities to learn: • q. X=heads • q. Y=heads|X=tails

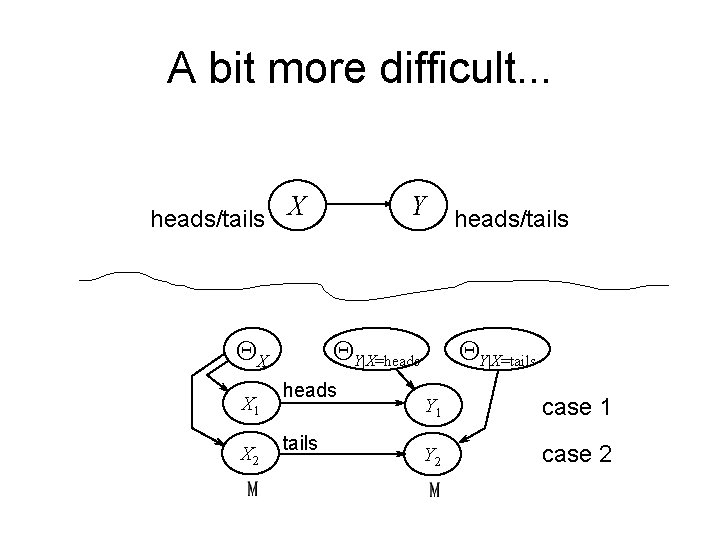
A bit more difficult. . . heads/tails X QY|X=heads QX X 1 X 2 Y heads tails heads/tails QY|X=tails Y 1 case 1 Y 2 case 2

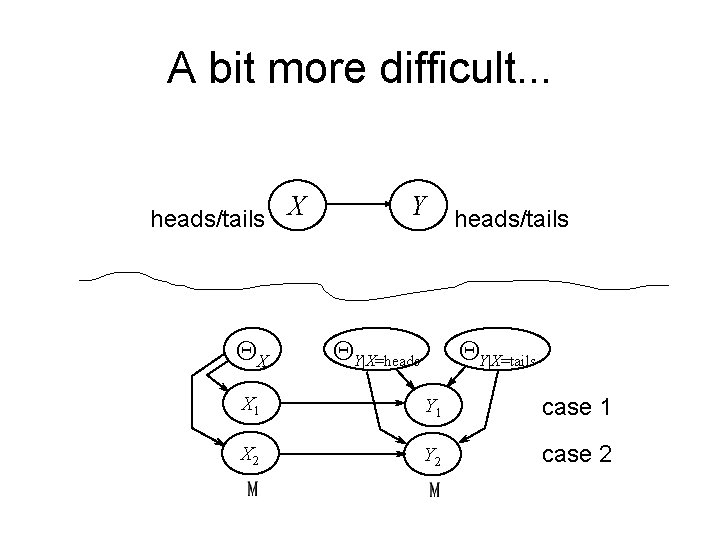
A bit more difficult. . . heads/tails X QX Y QY|X=heads/tails QY|X=tails X 1 Y 1 case 1 X 2 Y 2 case 2

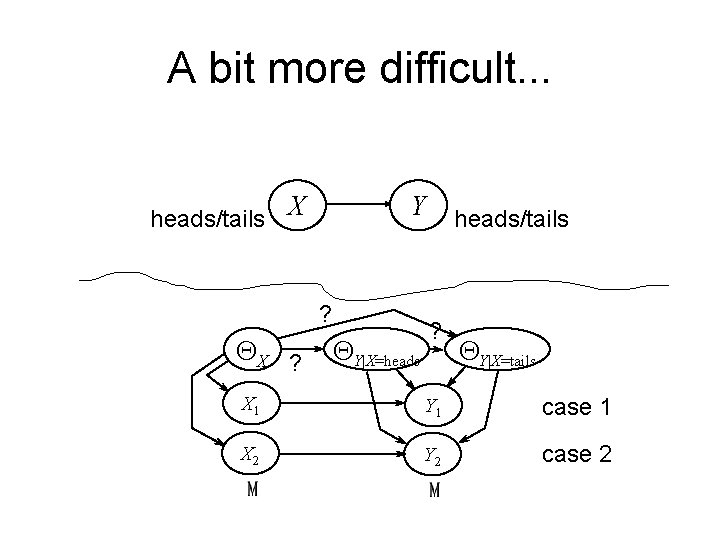
A bit more difficult. . . heads/tails X Y ? QX ? QY|X=heads/tails ? QY|X=tails X 1 Y 1 case 1 X 2 Y 2 case 2

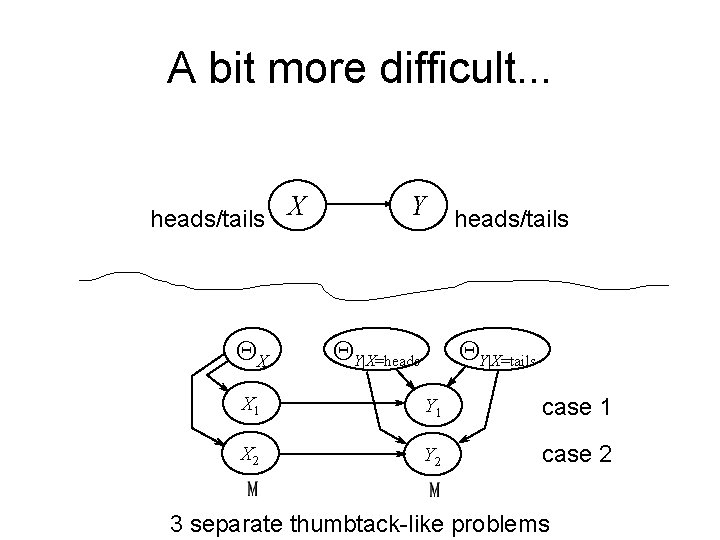
A bit more difficult. . . heads/tails X QX Y QY|X=heads/tails QY|X=tails X 1 Y 1 case 1 X 2 Y 2 case 2 3 separate thumbtack-like problems

In general … Learning probabilities in a Bayes net is straightforward if • Complete data • Local distributions from the exponential family (binomial, Poisson, gamma, . . . ) • Parameter independence • Conjugate priors

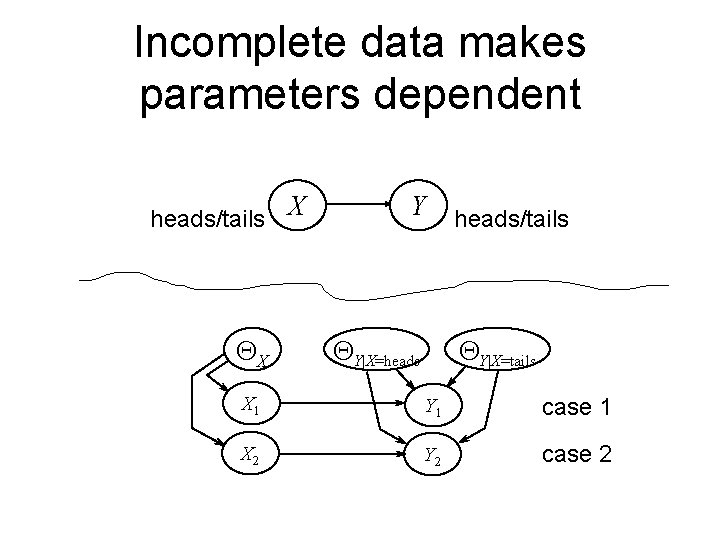
Incomplete data makes parameters dependent heads/tails X QX Y QY|X=heads/tails QY|X=tails X 1 Y 1 case 1 X 2 Y 2 case 2

Solution: Use EM • Initialize parameters ignoring missing data • E step: Infer missing values using current parameters • M step: Estimate parameters using completed data • Can also use gradient descent

Learning Bayes-net structure Given data, which model is correct? model 1: X Y model 2: X Y

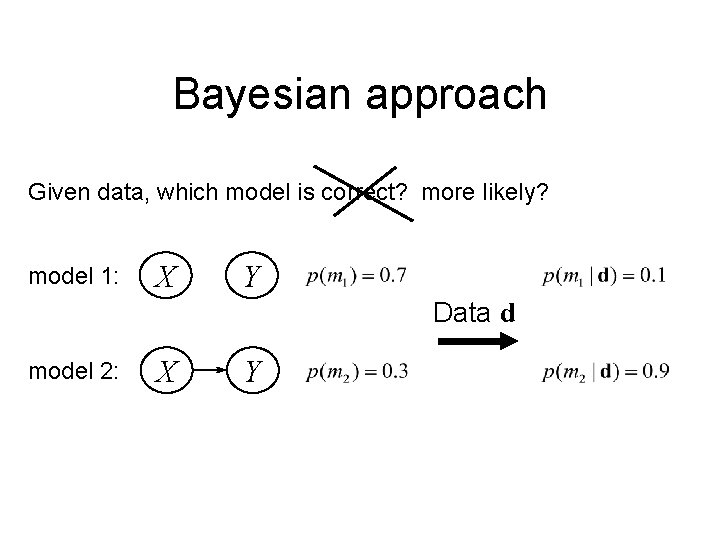
Bayesian approach Given data, which model is correct? more likely? model 1: X Y Data d model 2: X Y

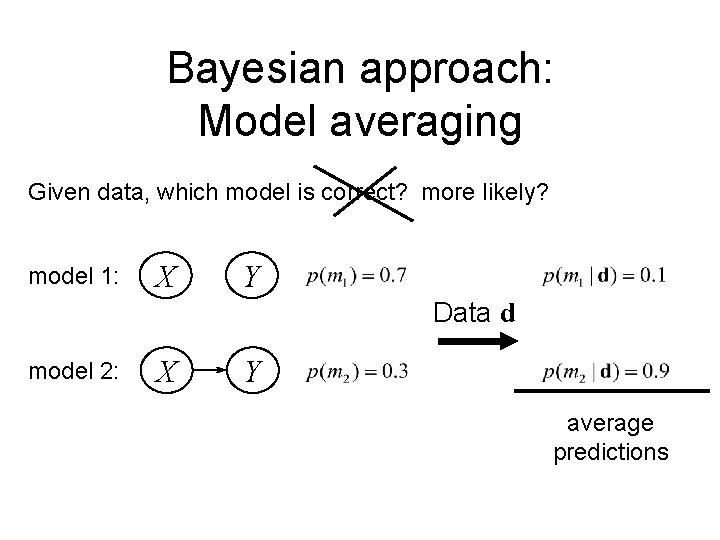
Bayesian approach: Model averaging Given data, which model is correct? more likely? model 1: X Y Data d model 2: X Y average predictions

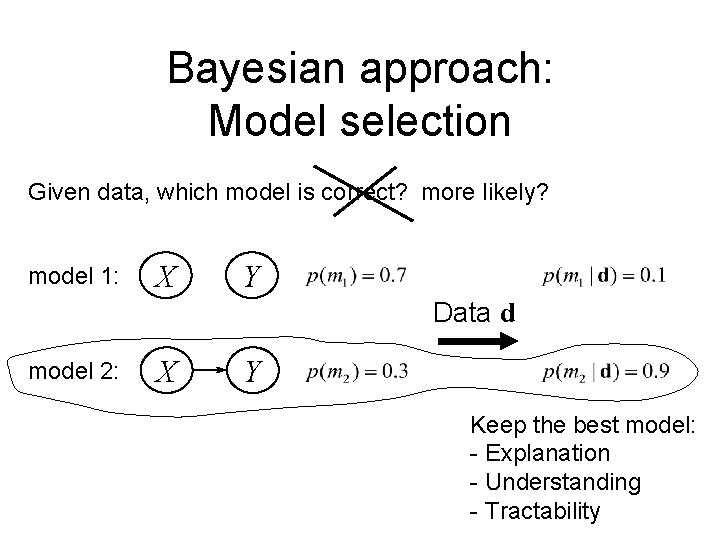
Bayesian approach: Model selection Given data, which model is correct? more likely? model 1: X Y Data d model 2: X Y Keep the best model: - Explanation - Understanding - Tractability

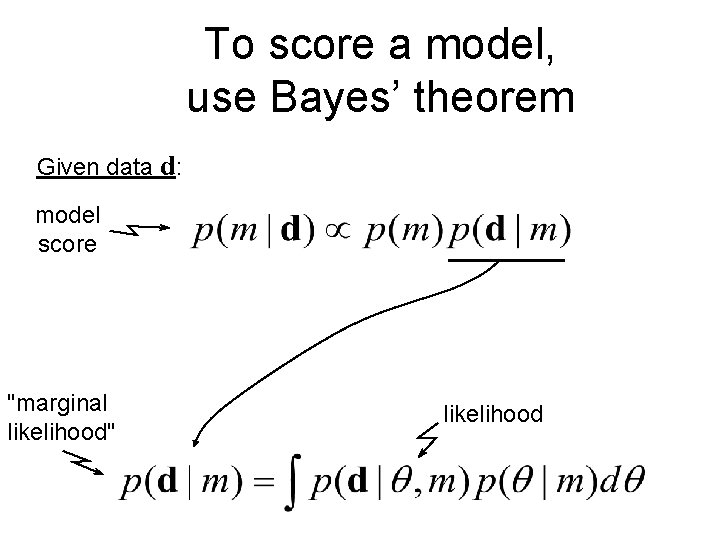
To score a model, use Bayes’ theorem Given data d: model score "marginal likelihood" likelihood

Thumbtack example X heads/tails conjugate prior

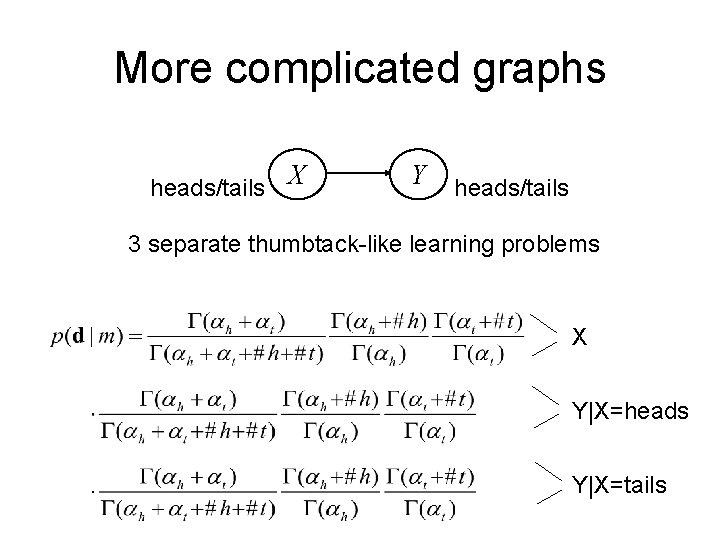
More complicated graphs heads/tails X Y heads/tails 3 separate thumbtack-like learning problems X Y|X=heads Y|X=tails

Model score for a discrete Bayes net

Computation of marginal likelihood Efficient closed form if • Local distributions from the exponential family (binomial, poisson, gamma, . . . ) • Parameter independence • Conjugate priors • No missing data (including no hidden variables)

Structure search • Finding the BN structure with the highest score among those structures with at most k parents is NP hard for k>1 (Chickering, 1995) • Heuristic methods initialize structure – Greedy with restarts – MCMC methods score all possible single changes any changes better? perform best change yes no return saved structure

Structure priors 1. All possible structures equally likely 2. Partial ordering, required / prohibited arcs 3. Prior(m) a Similarity(m, prior BN)

Parameter priors • All uniform: Beta(1, 1) • Use a prior Bayes net

Parameter priors Recall the intuition behind the Beta prior for the thumbtack: • The hyperparameters ah and at can be thought of as imaginary counts from our prior experience, starting from "pure ignorance" • Equivalent sample size = ah + at • The larger the equivalent sample size, the more confident we are about the long-run fraction

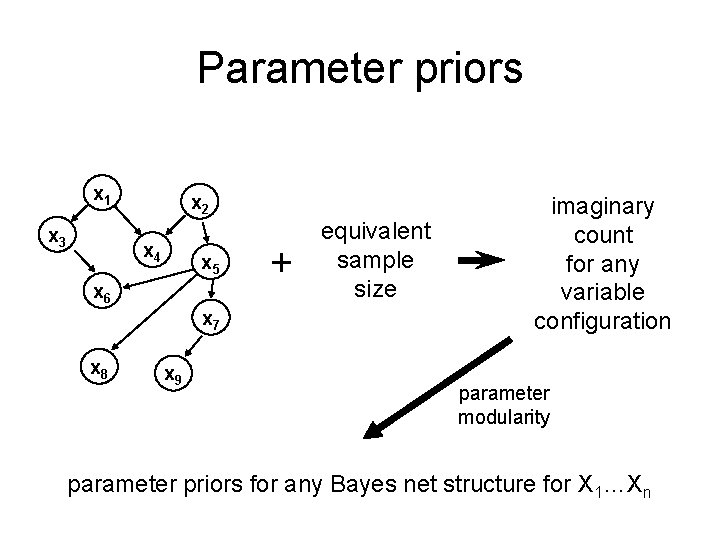
Parameter priors x 1 x 3 x 2 x 4 x 5 x 6 x 7 x 8 x 9 + equivalent sample size imaginary count for any variable configuration parameter modularity parameter priors for any Bayes net structure for X 1…Xn

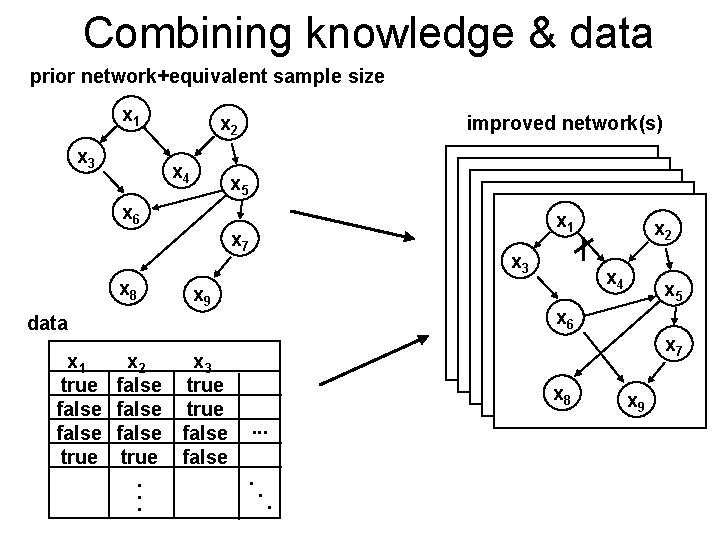
Combining knowledge & data prior network+equivalent sample size x 1 x 3 x 2 x 4 improved network(s) x 5 x 6 x 1 x 7 x 8 x 3 x 9 x 2 false true. . . x 3 true false x 4 x 5 x 6 data x 1 true false true x 2 x 7 x 8. . . x 9