LEARNING ASTRONOMY BY DOING ASTRONOMY ACTIVITY 1 MATHEMATICAL

LEARNING ASTRONOMY BY DOING ASTRONOMY ACTIVITY 1 – MATHEMATICAL AND SCIENTIFIC METHODS STEP 3 – SCALING AND SCALE FACTORS Let’s get started!

The authors of the workbook – Learning Astronomy by Doing Astronomy – have generally found that the biggest stumbling block in learning the methods of astronomy is not actually the math. Instead, it is figuring out the scale factor of an image. For example, we astronomers have to know how many arc seconds of a digital image of a celestial object are represented in a single picture element (pixel) of the camera they used. (Keep zooming into one of the images you took with your smart phone. See those “squares”? Those are pixels. )

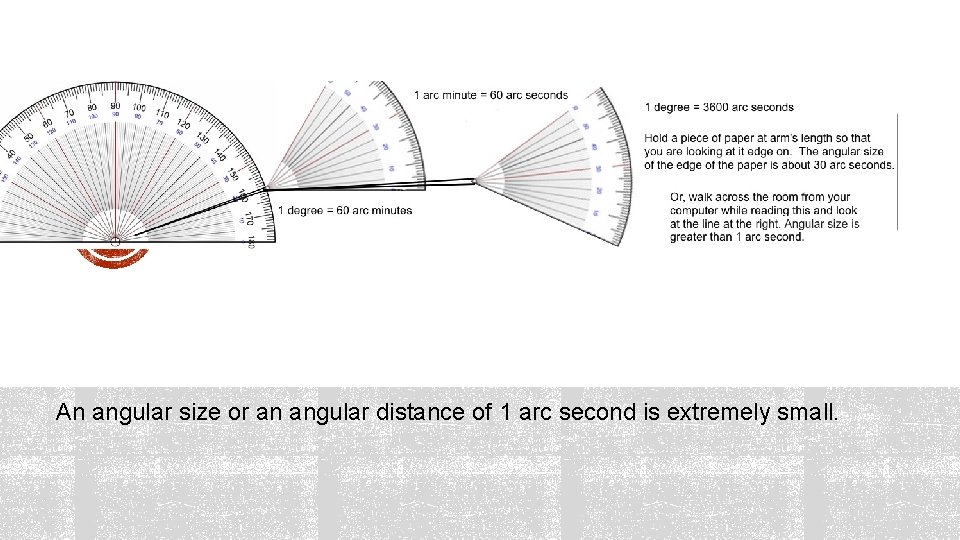
An angular size or an angular distance of 1 arc second is extremely small.

Here we have an imaginary landscape, mapped out with a hill, marshes, lake, creek, and a road. Before we can have any idea of the distances or sizes of any of these features, we need to have some way of translating size on the image versus size in the ‘real world’.

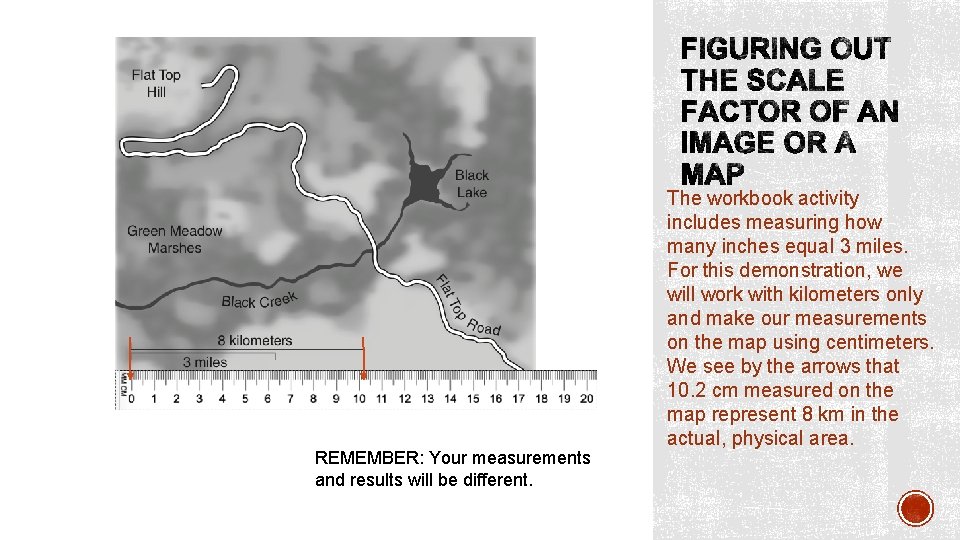
REMEMBER: Your measurements and results will be different. The workbook activity includes measuring how many inches equal 3 miles. For this demonstration, we will work with kilometers only and make our measurements on the map using centimeters. We see by the arrows that 10. 2 cm measured on the map represent 8 km in the actual, physical area.

How many kilometers are represented by 1 cm? You noted that the arrows indicated that 10. 2 cm measured on the map represent 8 km in the actual, physical area. This is NOT a conversion factor, it is a scaling factor. (Conversion would show 100 mm = 10 cm = 0. 1 m = 0. 0001 km. ) REMEMBER: Your measurements and results will be different.

The width of Black Lake ( E – W) is about 1. 1 cm. How wide is the actual lake in km? REMEMBER: Your measurements and results will be different.

Multiply both sides by the length measured on the map: 1. 1 Notice that we rounded off the answer. Now we need to figure out how to find the length of Black Creek, a feature that is not straight. Do we approximate or do we do more precise work?

Approximating the length using a straight ruler for a rambling creek: Start: 0. 5 cm ± 0. 2 cm End: 15. 5 cm ± 0. 2 cm Length: 15 cm ± 0. 4 cm We have an approximate answer and a statement of our uncertainties.

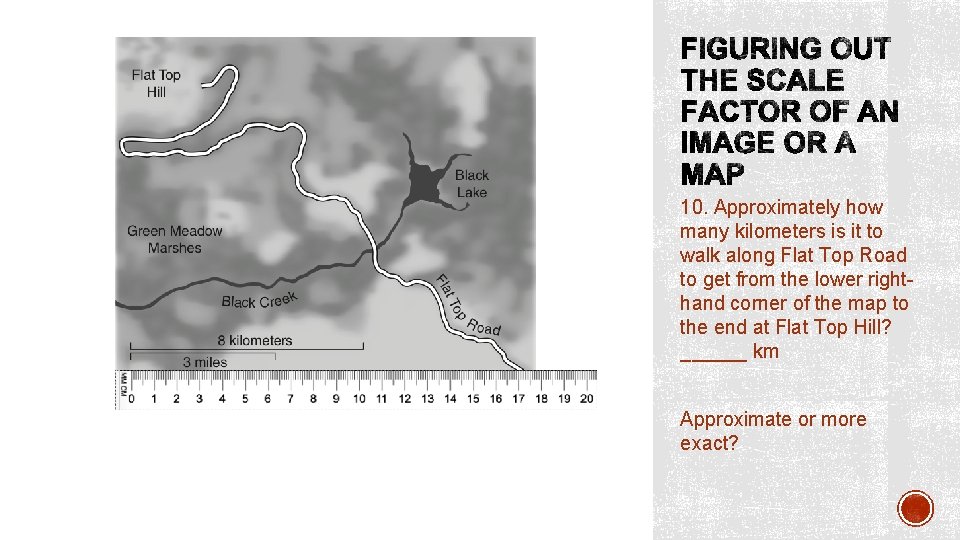
10. Approximately how many kilometers is it to walk along Flat Top Road to get from the lower righthand corner of the map to the end at Flat Top Hill? ______ km Approximate or more exact?

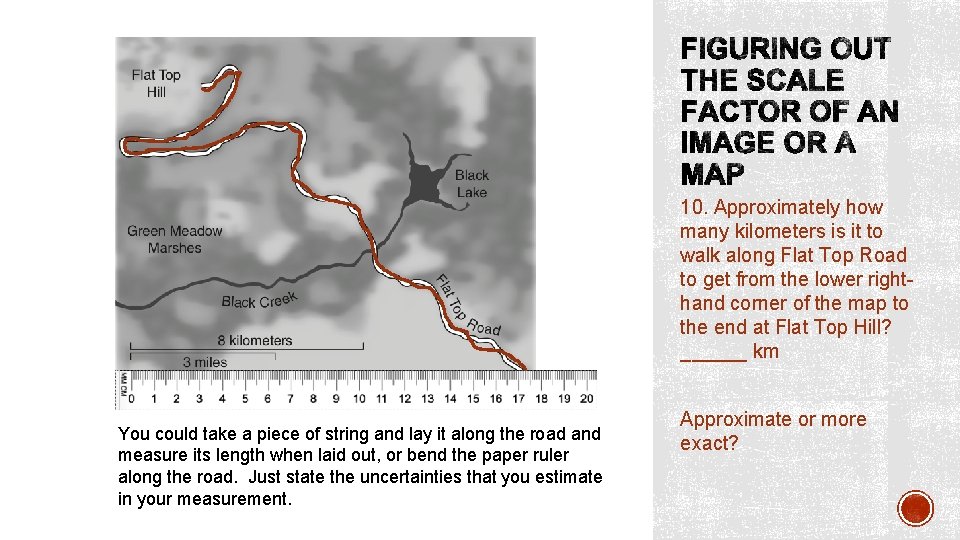
10. Approximately how many kilometers is it to walk along Flat Top Road to get from the lower righthand corner of the map to the end at Flat Top Hill? ______ km You could take a piece of string and lay it along the road and measure its length when laid out, or bend the paper ruler along the road. Just state the uncertainties that you estimate in your measurement. Approximate or more exact?

Your turn: 8. If you walked at 2 kilometers per hour (km/h), how long would the trip take you? ______ hours (You are a very slow walker!) Distance traveled is equal to your velocity times the amount of time it took you to travel: d = vt Rearrange the equation: The amount of time it will take will equal the distance you need to travel divided by your velocity: t = d/v