Le pendule simple Points essentiels Retour sur la

Le pendule simple

Points essentiels Retour sur la dynamique de rotation Moment de force; Moment d’inertie; Approximation des petits angles Énergie dans un pendule simple Travail personnel

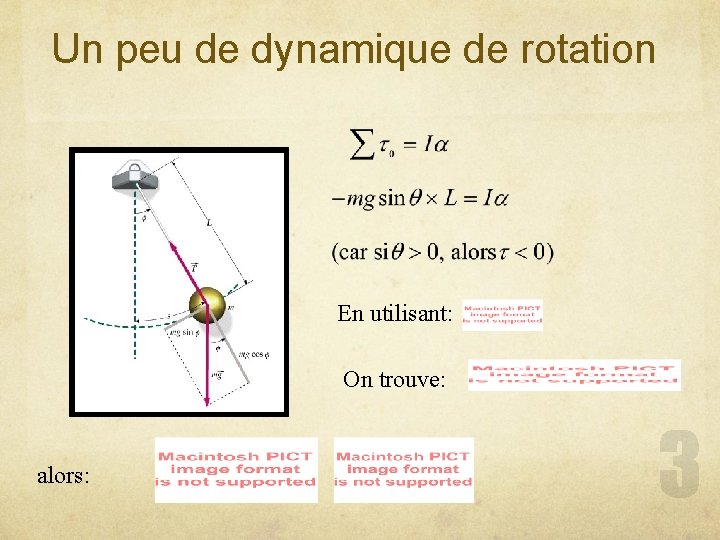
Un peu de dynamique de rotation En utilisant: On trouve: alors:

En utilisant l’approximation des petits angles alors: équation du genre: (en radian) Solution: avec: et

Conclusion 1. La période T est indépendante de l’amplitude (qmax) pour des petits angles. 2. La période T est indépendante de la masse m.

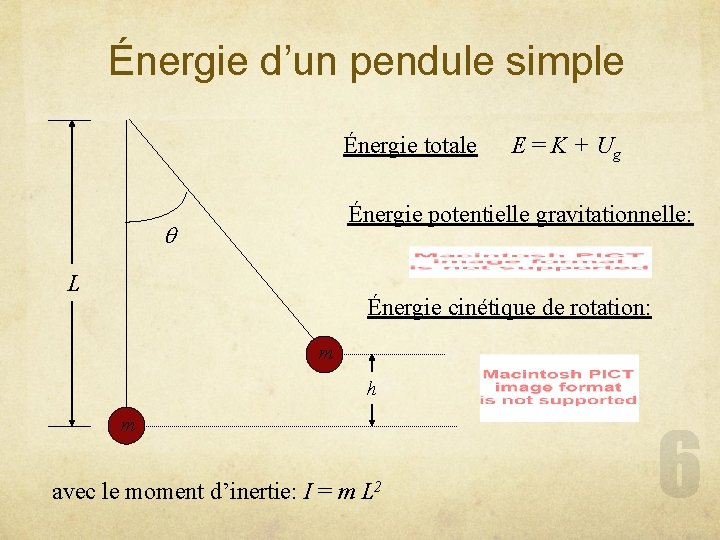
Énergie d’un pendule simple Énergie totale E = K + Ug Énergie potentielle gravitationnelle: q L Énergie cinétique de rotation: m h m avec le moment d’inertie: I = m L 2

Énergie d’un pendule simple (suite) On sait que: alors: et: Pour des petits angles: (réf. p. 404) alors: soit: (en radian) (en radian/s) (en Joule) cos q 1 - ½ q 2 … (en radian)

Énergie d’un pendule simple (suite) En prenant: on obtient: Remarque: L’énergie dans un mouvement harmonique simple est proportionnelle au carré de l’amplitude !

Exercice 31 (page 30) La masse de 20 g d’un pendule simple de longueur 0, 8 m est lâchée lorsque le fil fait un angle de 30° avec la verticale. a)Trouvez la période; b)La position angulaire q(t); c)L’énergie mécanique; d)Le module de la vitesse de la masse à q = 15°

Exercice 31 (suite) a) On sait que b) Pour la fonction position

Exercice 31 (suite) c) On peut calculer l’énergie mécanique totale au point de départ, c’est-à-dire, lorsque le pendule se trouve à la position angulaire q = 30°. À ce moment, toute l’énergie se retrouve sous forme d’énergie potentielle gravitationnelle, soit: d) Pour obtenir la vitesse à q = 15°, on utilise la fonction vitesse:

Exercice 31 (suite) d) Pour obtenir la phase à q = 15°, on utilise la fonction position: On trouve , si l’on désire un temps positif, on ajoute 2 p à l’angle. Il ne faut pas oublier qu’il y a deux vitesses possibles pour une position donnée. Alors les valeurs possibles de la phase sont:

Exercice 31 (suite) Pour obtenir la vitesse tangentielle, on multiplie par le rayon du mouvement (ici la longueur du pendule), alors: On obtient v = ± 1, 27 m/s. Puisqu’on demande le module de la vitesse, alors v = 1, 27 m/s!

Travail personnel Faire l’exemple: 1. 9. La question: 4. Les exercices: 27, 31 et 79. Les problèmes 5 et 13