LCM An Efficient Algorithm for Enumerating Frequent Closed

LCM: An Efficient Algorithm for Enumerating Frequent Closed Item Sets Linear time Closed itemset Miner Takeaki Uno Tatsuya Asai Hiroaki Arimura Yuzo Uchida National Institute of Informatics Kyushu University 19/Nov/2003 FIMI 2003

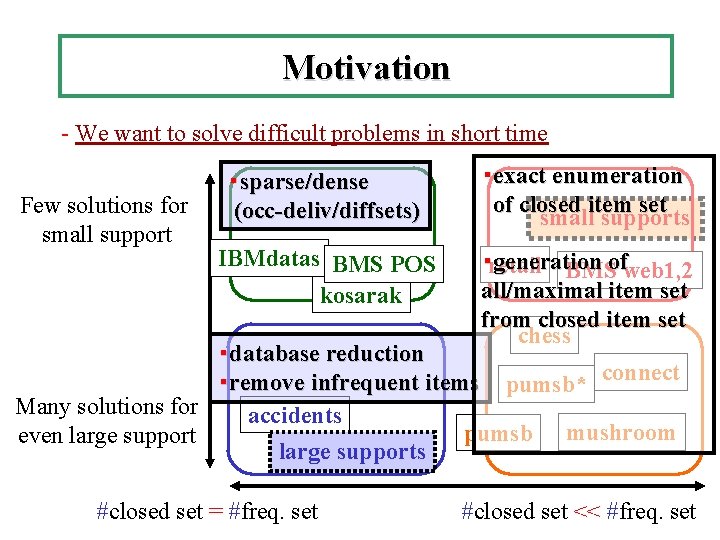
Motivation - We want to solve difficult problems in short time Few solutions for small support ・sparse/dense (occ-deliv/diffsets) ・exact enumeration of closed item set small supports IBMdatas BMS POS kosarak ・retail generation BMSofweb 1, 2 all/maximal item set from closed item set chess ・database reduction ・remove infrequent items pumsb* connect Many solutions for accidents pumsb mushroom even large supports #closed set = #freq. set #closed set << #freq. set

Outline of Our Research - Exact enumeration of closed item sets (no sophisticated pruning, post processing, nor memory for obtained closed item sets) - Enumerate all/maximal frequent item sets using closed item set - Algorithms for updating occurrences/maximality check in dense/sparse cases, and their adaptive hybrid - Save additional memory use (right first sweep, adjacency matrix only for large transactions)

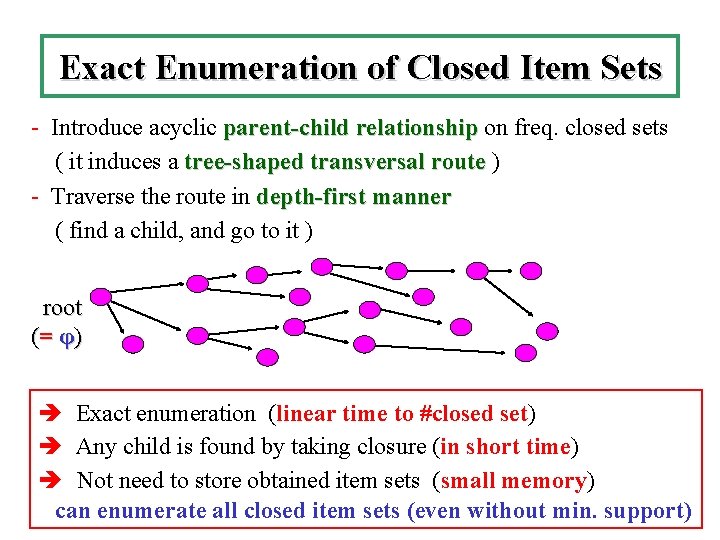
Exact Enumeration of Closed Item Sets - Introduce acyclic parent-child relationship on freq. closed sets ( it induces a tree-shaped transversal route ) - Traverse the route in depth-first manner ( find a child, and go to it ) root (= φ ) Exact enumeration (linear time to #closed set) Any child is found by taking closure (in short time) Not need to store obtained item sets (small memory) can enumerate all closed item sets (even without min. support)

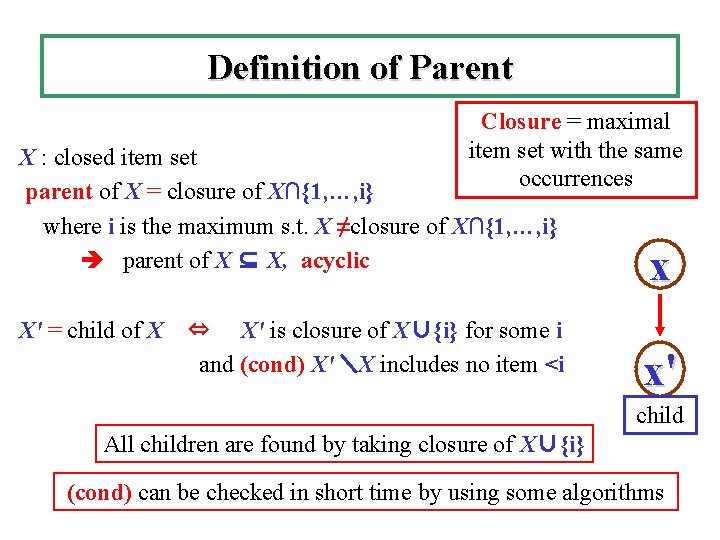
Definition of Parent Closure = maximal item set with the same occurrences X : closed item set parent of X = closure of X∩{1, …, i} where i is the maximum s. t. X ≠closure of X∩{1, …, i} parent of X ⊆ X, acyclic X' = child of X ⇔ X' is closure of X∪{i} for some i and (cond) X'＼X includes no item <i x x' child All children are found by taking closure of X∪{i} (cond) can be checked in short time by using some algorithms

Adaptive Hybrid Algorithm Computation of Occurrences X∪{i} for Sparse and Dense Cases - In sparse case, by tracing items of each occurrence of X (occurrence deliver : maybe a known technique) - In dense case, use diffsets (proposed by Zaki) We choose best one according to estimations of computation time in each iterations

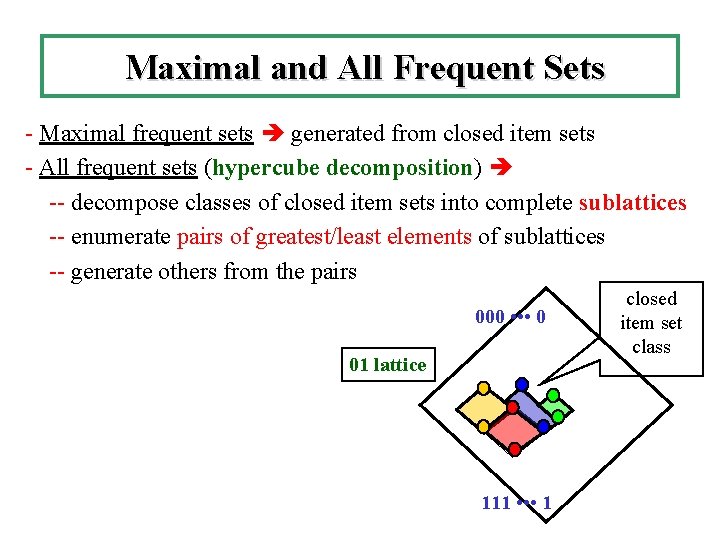
Maximal and All Frequent Sets - Maximal frequent sets generated from closed item sets - All frequent sets (hypercube decomposition) -- decompose classes of closed item sets into complete sublattices -- enumerate pairs of greatest/least elements of sublattices -- generate others from the pairs 000 • • • 0 01 lattice 111 • • • 1 closed item set class

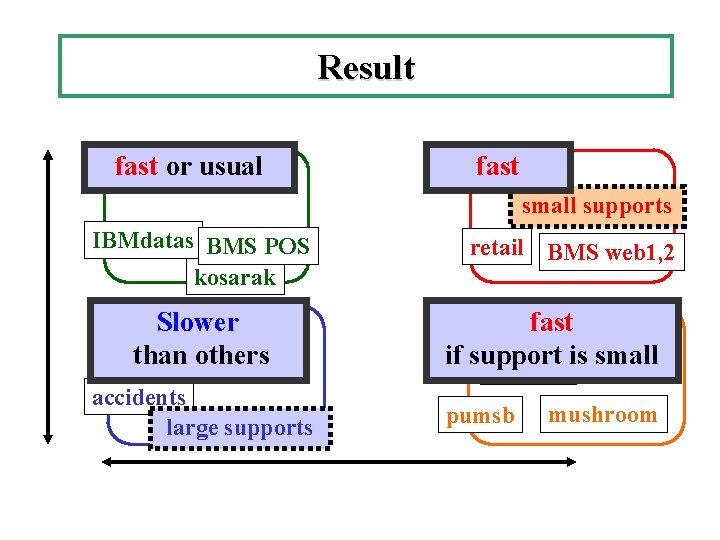
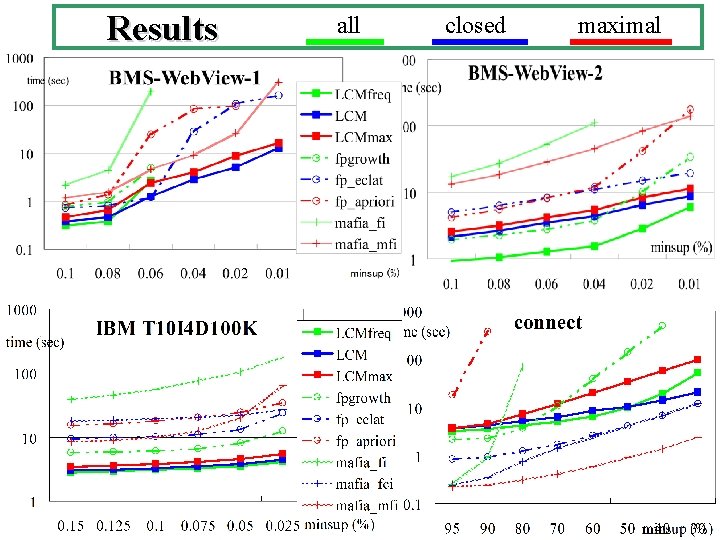
Result fast or usual fast small supports IBMdatas BMS POS kosarak Slower than others accidents large supports retail BMS web 1, 2 chess fast if support small pumsb*isconnect pumsb mushroom

Conclusion - For data sets s. t. #freq. closed sets << #freq. sets - large business datasets: BMS-web 1, 2, retails - machine learning datasets with small supports: UCI repository exact enumeration of closed item sets and hypercube decomposition perform well Fast without pruning, trie, For further speed up other existing method - These techniques are orthogonal to other techniques, ( ・database reduction, ・pruning infrequent items, … ) we can do better for large supports / accidents (blue area). - Parameter of hybrid is not tuned not fast for kosarak, IBMdatas now faster

We think… ● What are the real problem (bottleneck) ? ---- Mining structured item sets (closed item sets, association rule with threshold, … ) ● Is it only a counting problem ? ---- for all frequent item set mining, Yes. the problem is how to make the occurrences of an item set from other item sets (choose best way, represent ● Is maximal item set useful ? ---- closed item set is useful!! have an application for classification, association rule mining

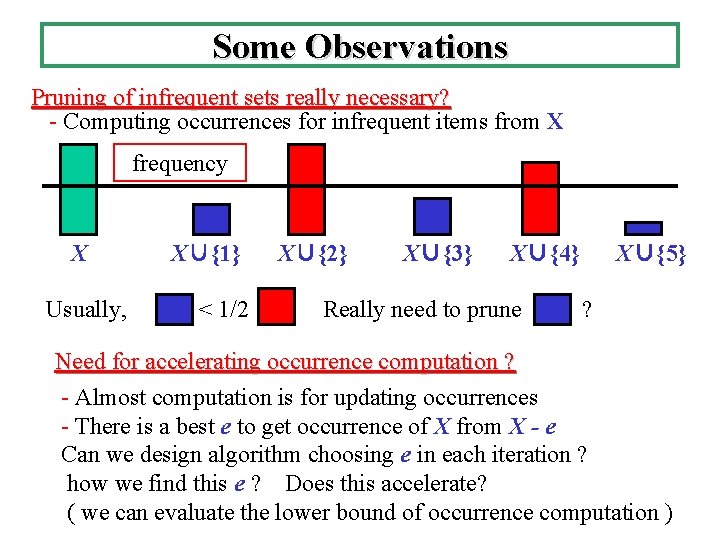
Some Observations Pruning of infrequent sets really necessary? - Computing occurrences for infrequent items from X frequency X Usually, X∪{1} < 1/2 X∪{2} X∪{3} X∪{4} Really need to prune X∪{5} ? Need for accelerating occurrence computation ? - Almost computation is for updating occurrences - There is a best e to get occurrence of X from X - e Can we design algorithm choosing e in each iteration ? how we find this e ? Does this accelerate? ( we can evaluate the lower bound of occurrence computation )

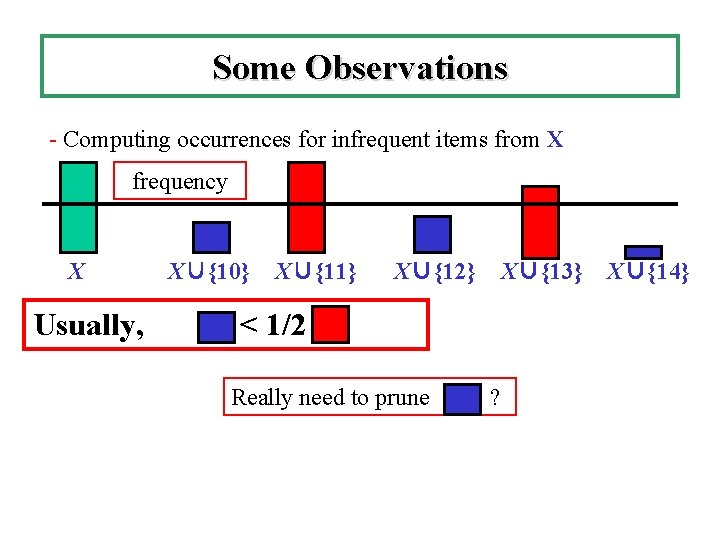
Some Observations - Computing occurrences for infrequent items from X frequency X Usually, X∪{10} X∪{11} X∪{12} X∪{13} < 1/2 Really need to prune ? X∪{14}

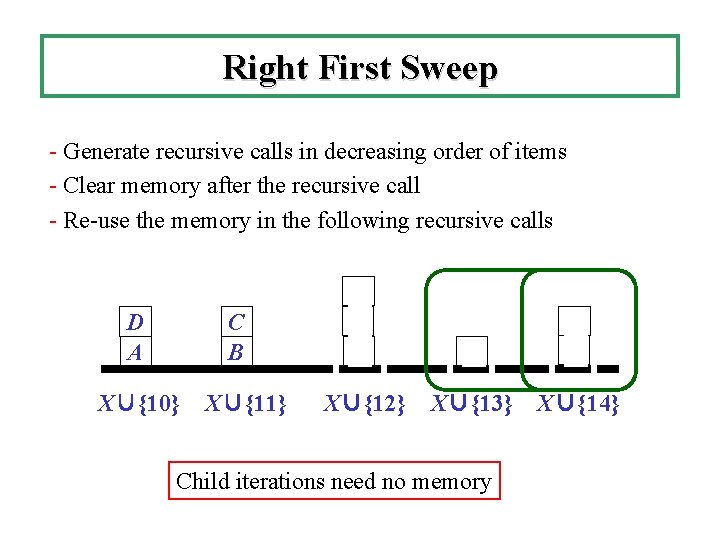
Right First Sweep - Generate recursive calls in decreasing order of items - Clear memory after the recursive call - Re-use the memory in the following recursive calls D A C B X∪{10} X∪{11} D B A E D A X∪{12} X∪{13} X∪{14} Child iterations need no memory

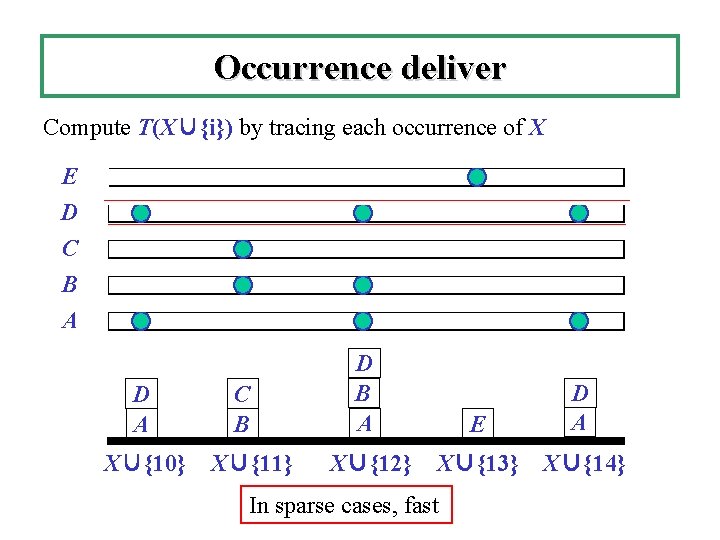
Occurrence deliver Compute T(X∪{i}) by tracing each occurrence of X E D C B A D A X∪{10} C B X∪{11} D B A E D A X∪{12} X∪{13} X∪{14} In sparse cases, fast

Checking (cond) of Closure - Check (cond) closure of X∪{i}＼X includes no item <i - In sparse case, find an occurrence not including j, for all possible item j - In dense case, update occurrences of all frequent X∪{j}, and compute T(X∪{i}∪{j}) C A X∪{1} C B A ・・・ C B A X∪{2} ・・・ X∪{i} X∪{14} Quite faster than computing the closure of X∪{i}

Results all closed maximal