LAY OUT CALCULATIONS TYPICAL YARD Why Layout Calculations

LAY OUT CALCULATIONS

TYPICAL YARD

Why Layout Calculations? • To fix correct position of T/out wrt existing track in case of yard remodeling • To avoid kinks & sharp curvatures • To design new layouts in case of new construction • To ensure safety • For space economization

When needed ? • Open Line engineers Ø To rectify defective layouts Ø For yard remodeling works • Construction Engineers Ø For Gauge conversion works Ø For doubling works Ø For yard remodeling works

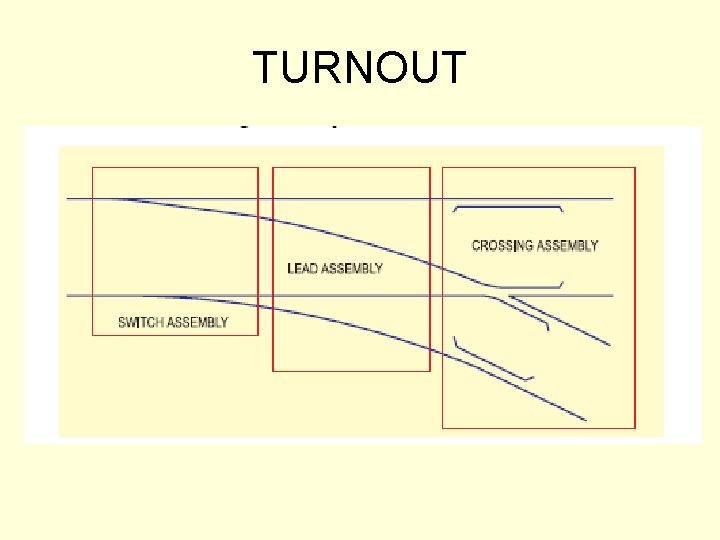
TURNOUT

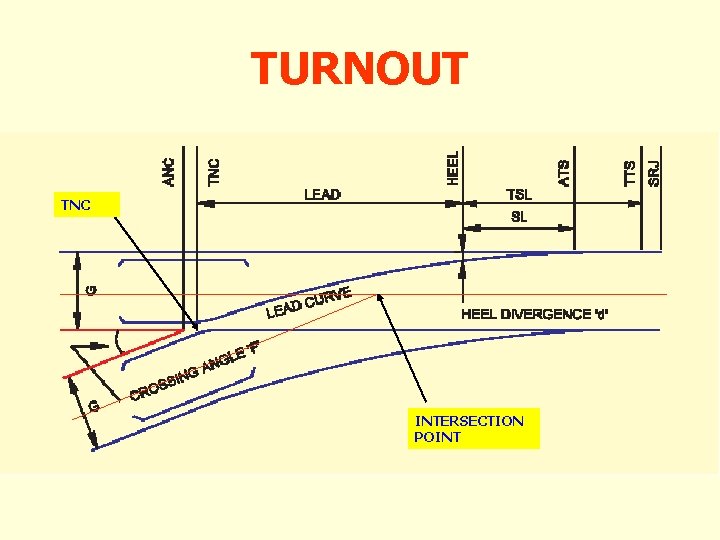
TURNOUT TNC INTERSECTION POINT

Provisions of IRPWM • Para 410(2) § Turn outs in passenger running lines over which passenger trains are received & dispatched should be laid with crossing, not sharper than 1 in 12 for straight switch. § In exceptional circumstances, 1 in 8 1/2 curved switch may be laid; due to space constraint. § Sharper crossings may also be used when T/O is taking off from outside of a curve keeping radius of lead curve within 350 m (BG) (D=5)

Provisions of IRPWM • Turn in curve may be allowed up to 220 m (BG) (D=8) subject to - Turn in curve on PSC or ST sleepers only, with sleeper spacing same as for main line. - Full ballast profile as for main line track. • Emergency X - overs between double or multiple lines which are laid only in the trailing direction may be laid with 1 in 8. 5 crossings.

Provisions of IRPWM In case of - 1 in 8. 5 T/Os with straight switches on passenger lines, speed restricted to 10 Kmph - 1 in 8. 5 T/Os with straight swithes on nonpassenger lines, speed restricted to 15 Kmph • Para 410(3) ØPermissible speed for T/Os taking off from inside of the curve shall be decided by taking resultant radius of lead curve Ø 1 in 8. 5 T/Os not to be laid on inside of curves

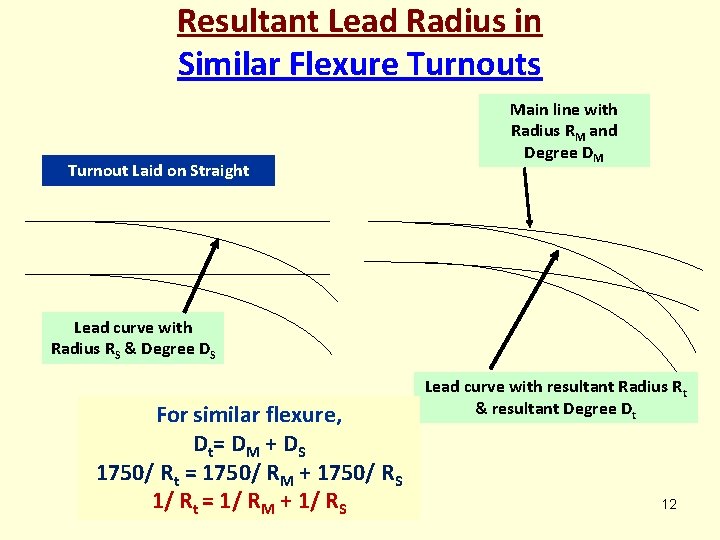
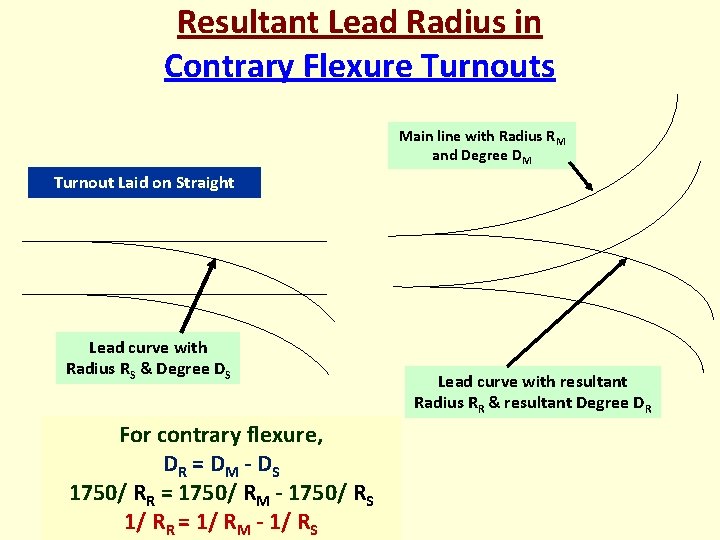
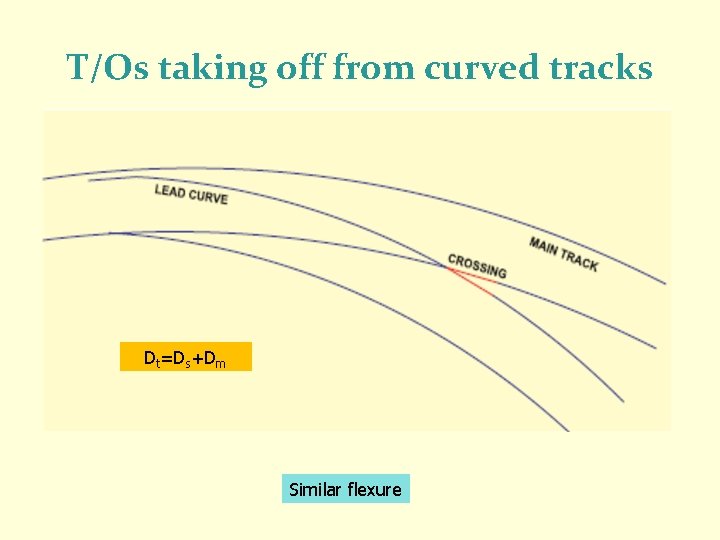
TYPES OF LAYOUT -T/Os taking off from straight track -T/Os taking off from curved tracks • DS is the degree of T/O curve (lead curve) taking off from straight • DM is the degree of main line curve • DR is the resultant degree of T/O curve (lead curve) when taking off from curved main line

Resultant Lead Radius in Similar Flexure Turnouts Turnout Laid on Straight Main line with Radius RM and Degree DM Lead curve with Radius RS & Degree DS For similar flexure, Dt= D M + D S 1750/ Rt = 1750/ RM + 1750/ RS 1/ Rt = 1/ RM + 1/ RS Lead curve with resultant Radius Rt & resultant Degree Dt 12

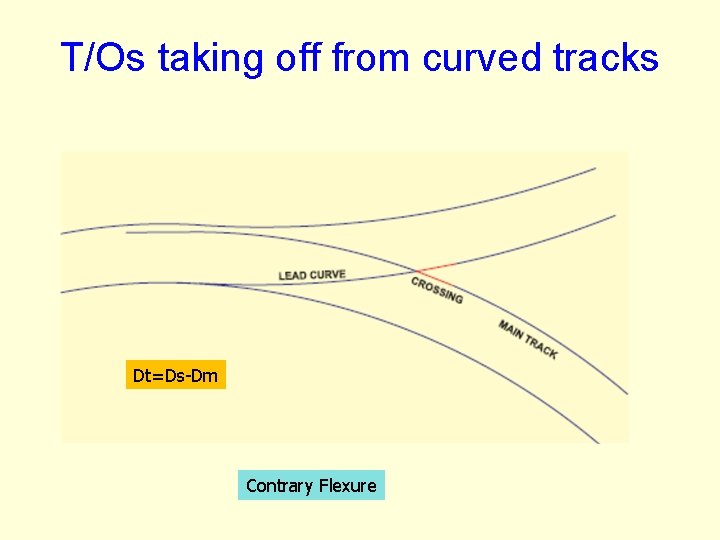
Resultant Lead Radius in Contrary Flexure Turnouts Main line with Radius RM and Degree DM Turnout Laid on Straight Lead curve with Radius RS & Degree DS For contrary flexure, DR = D M - D S 1750/ RR = 1750/ RM - 1750/ RS 1/ RR = 1/ RM - 1/ RS Lead curve with resultant Radius RR & resultant Degree DR

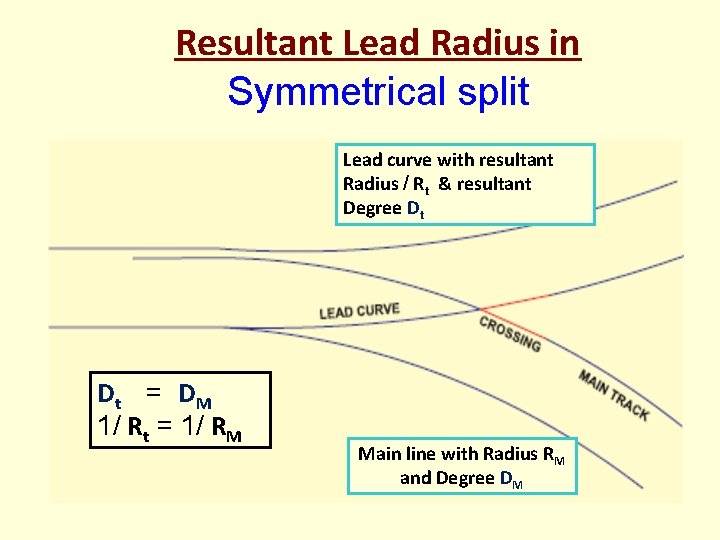
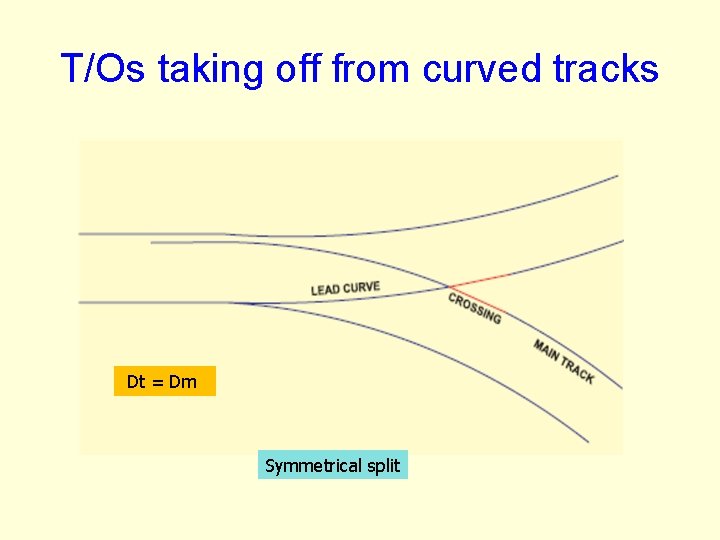
Resultant Lead Radius in Symmetrical split Lead curve with resultant Radius / Rt & resultant Degree Dt Dt = DM 1/ Rt = 1/ RM Main line with Radius RM and Degree DM

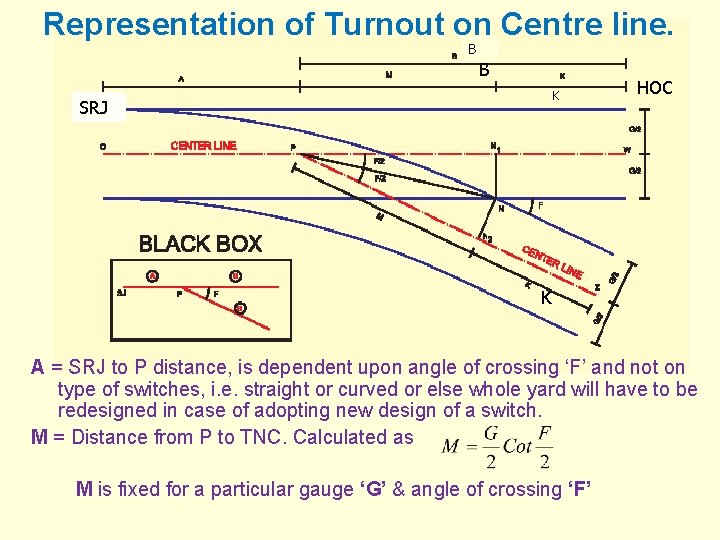
Representation of Turnout on Centre line. BB B K SRJ HOC K A = SRJ to P distance, is dependent upon angle of crossing ‘F’ and not on type of switches, i. e. straight or curved or else whole yard will have to be redesigned in case of adopting new design of a switch. M = Distance from P to TNC. Calculated as M is fixed for a particular gauge ‘G’ & angle of crossing ‘F’

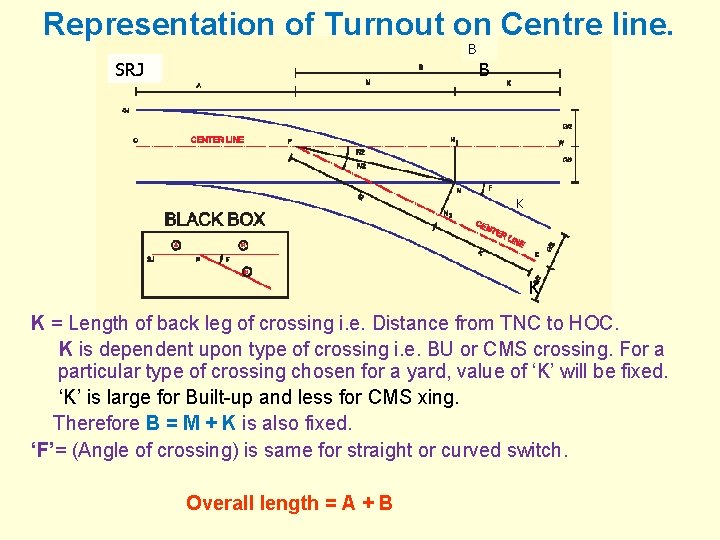
Representation of Turnout on Centre line. BB SRJ B K K K = Length of back leg of crossing i. e. Distance from TNC to HOC. K is dependent upon type of crossing i. e. BU or CMS crossing. For a particular type of crossing chosen for a yard, value of ‘K’ will be fixed. ‘K’ is large for Built-up and less for CMS xing. Therefore B = M + K is also fixed. ‘F’= (Angle of crossing) is same for straight or curved switch. Overall length = A + B

A TURNOUT Ø A, M and K are known as turnout parameters Ø For a particular gauge and angle of crossing , M is fixed Ø K is the length of back leg of Xing and will depend on type of Xing, built up or CMS Ø A is also dependent on angle of xing and not on type of switch Ø Therefore for a given gauge, crossing angle and crossing type (BU or CMS), value of these turnout parameters i. e. ‘A’, ‘M’ & ‘K’ are fixed. i. e. The T/O are fixed.

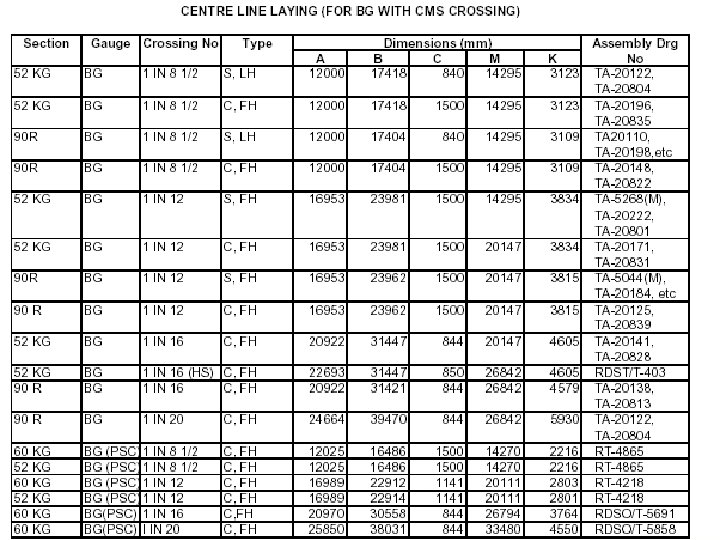
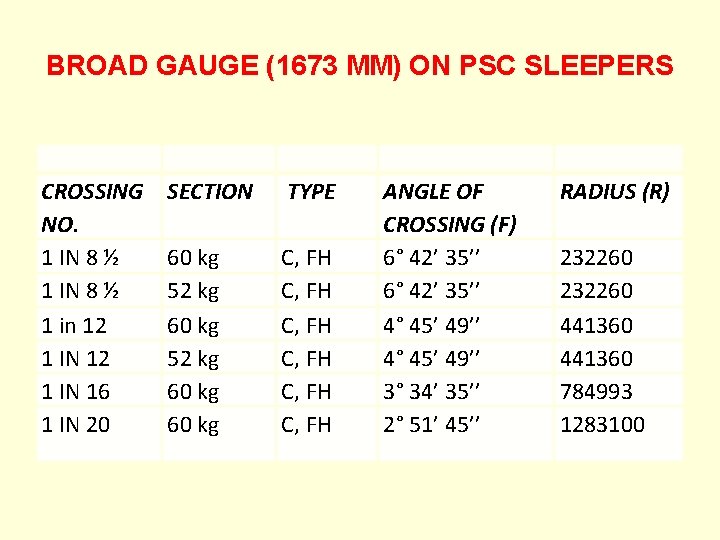
BROAD GAUGE (1673 MM) ON PSC SLEEPERS CROSSING NO. 1 IN 8 ½ 1 in 12 1 IN 16 1 IN 20 SECTION TYPE 60 kg 52 kg 60 kg C, FH C, FH ANGLE OF CROSSING (F) 6° 42’ 35’’ 4° 45’ 49’’ 3° 34’ 35’’ 2° 51’ 45’’ RADIUS (R) 232260 441360 784993 1283100

TYPE OF CONNECTIONS • Connection to non parallel tracks (divergent) • Connection to parallel tracks

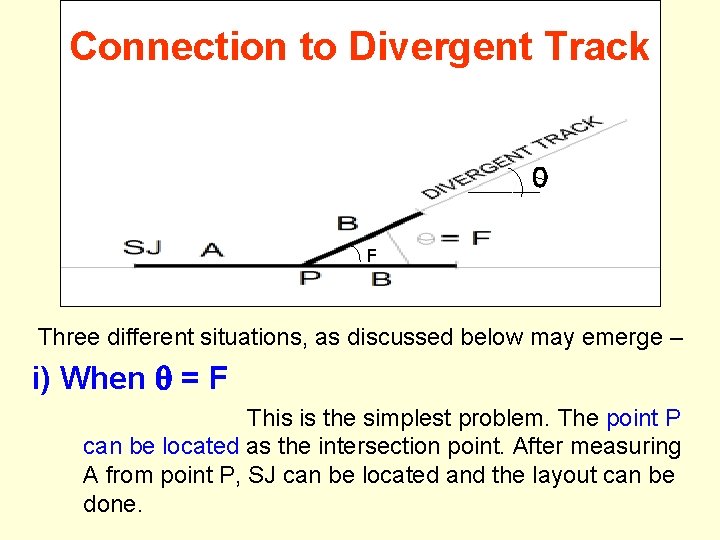
Connection to Divergent Track - F Three different situations, as discussed below may emerge – i) When = F This is the simplest problem. The point P can be located as the intersection point. After measuring A from point P, SJ can be located and the layout can be done.

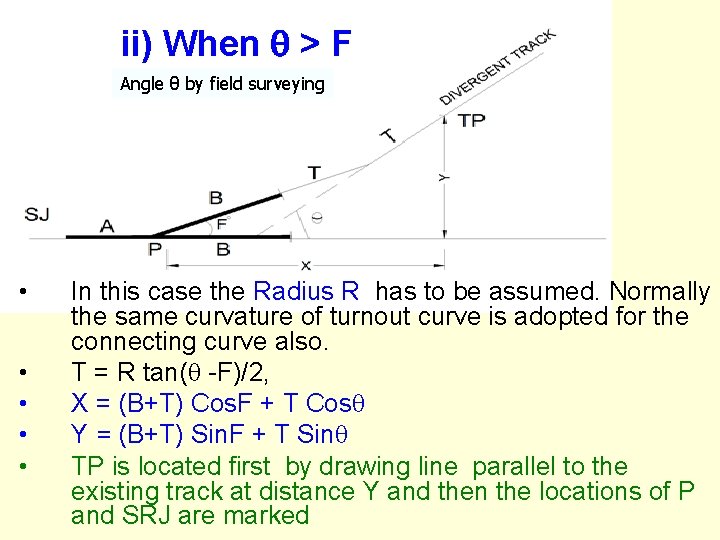
ii) When > F Angle θ by field surveying • • • In this case the Radius R has to be assumed. Normally the same curvature of turnout curve is adopted for the connecting curve also. T = R tan( -F)/2, X = (B+T) Cos. F + T Cos Y = (B+T) Sin. F + T Sin TP is located first by drawing line parallel to the existing track at distance Y and then the locations of P and SRJ are marked

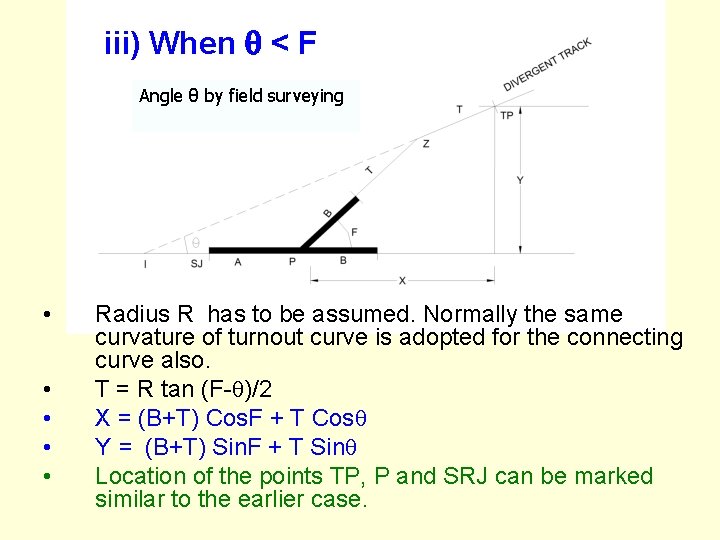
iii) When < F Angle θ by field surveying • • • Radius R has to be assumed. Normally the same curvature of turnout curve is adopted for the connecting curve also. T = R tan (F- )/2 X = (B+T) Cos. F + T Cos Y = (B+T) Sin. F + T Sin Location of the points TP, P and SRJ can be marked similar to the earlier case.

Connections To Straight Parallel Tracks • Type of Layout connections between straight parallel tracks depends upon the distance between them & space availability in the Yard. • Accordingly distance between the two tracks may be treated as NORMAL or LARGE distance.

Connections To Straight Parallel Tracks 1. With normal distance between tracks 2. With large distance between tracks (I) with no straight between reverse curves (II) with a straight between reverse curves

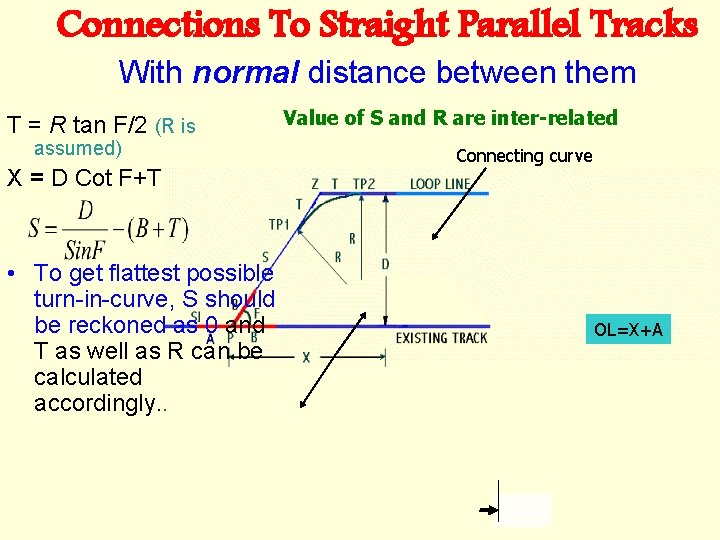
Connections To Straight Parallel Tracks With normal distance between them T = R tan F/2 (R is assumed) X = D Cot F+T • To get flattest possible turn-in-curve, S should be reckoned as 0 and T as well as R can be calculated accordingly. . Value of S and R are inter-related Connecting curve OL=X+A

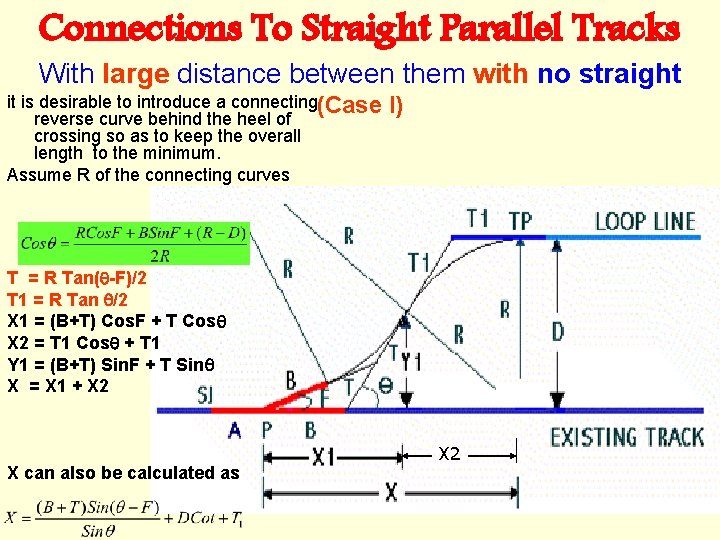
Connections To Straight Parallel Tracks With large distance between them with no straight it is desirable to introduce a connecting(Case reverse curve behind the heel of crossing so as to keep the overall length to the minimum. Assume R of the connecting curves I) T = R Tan( -F)/2 T 1 = R Tan /2 X 1 = (B+T) Cos. F + T Cos X 2 = T 1 Cos + T 1 Y 1 = (B+T) Sin. F + T Sin X = X 1 + X 2 X can also be calculated as X 2

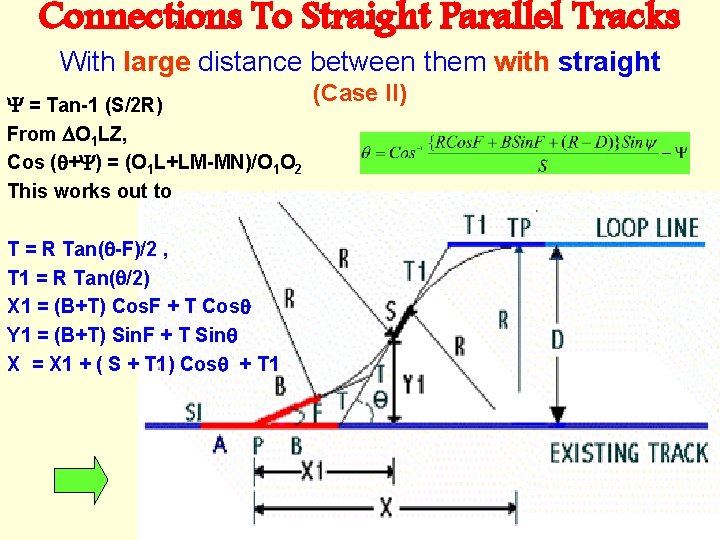
Connections To Straight Parallel Tracks With large distance between them with straight = Tan-1 (S/2 R) From O 1 LZ, Cos ( + ) = (O 1 L+LM-MN)/O 1 O 2 This works out to T = R Tan( -F)/2 , T 1 = R Tan( /2) X 1 = (B+T) Cos. F + T Cos Y 1 = (B+T) Sin. F + T Sin X = X 1 + ( S + T 1) Cos + T 1 (Case II)

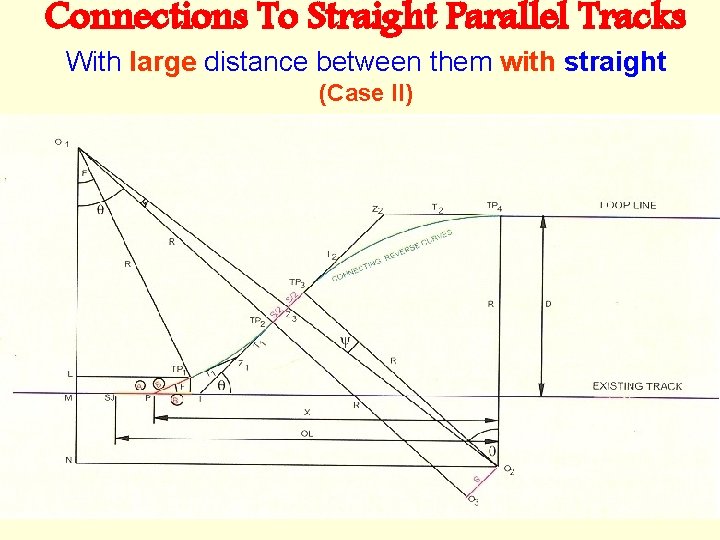
Connections To Straight Parallel Tracks With large distance between them with straight (Case II)

CROSSOVER

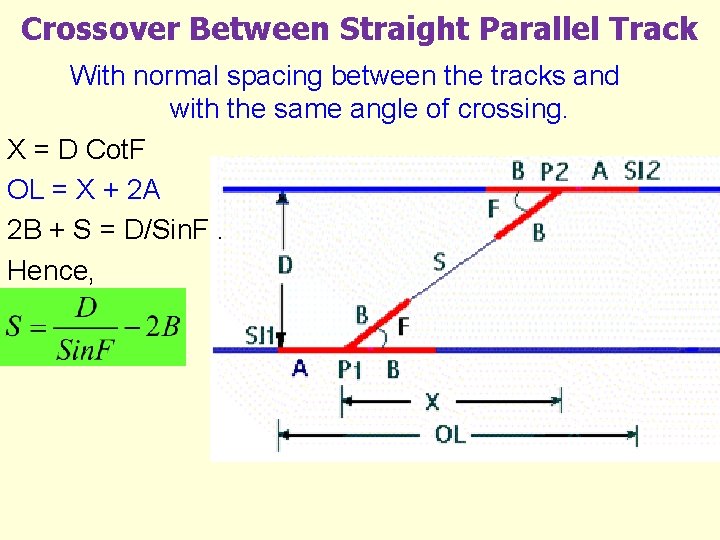
Crossover Between Straight Parallel Track With normal spacing between the tracks and with the same angle of crossing. X = D Cot. F OL = X + 2 A 2 B + S = D/Sin. F. Hence,

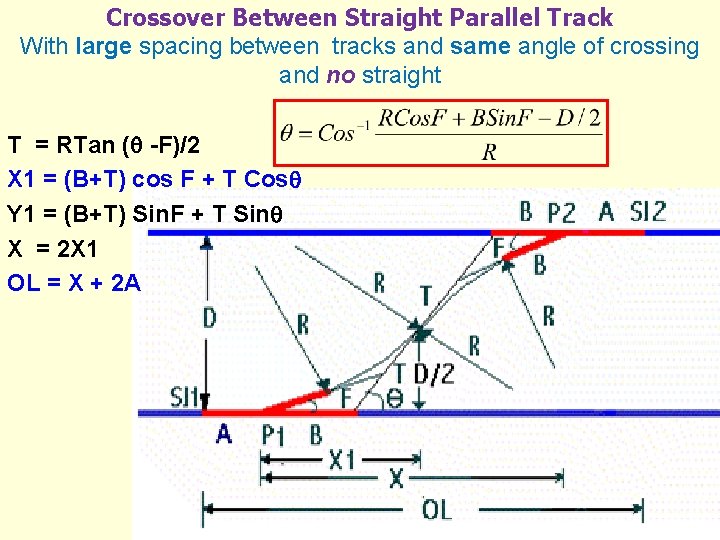
Crossover Between Straight Parallel Track With large spacing between tracks and same angle of crossing and no straight T = RTan ( -F)/2 X 1 = (B+T) cos F + T Cos Y 1 = (B+T) Sin. F + T Sin X = 2 X 1 OL = X + 2 A

Crossover Between Straight Parallel Track With large spacing between tracks and same angle of crossing and no straight - ‘R’ is assumed same as that lead curve radius of T/out. - D’ is known from actual field measurement. - Type of T/out is decided. Accordingly value of T/out parameters A, B will be known. - Ө, T, X 1, Y 1 is calculated from expressions. - One of the point P 1 or P 2 is to be fixed on field considering obligatory points if any. - other points can be fixed w. r. t. P 1 or P 2.

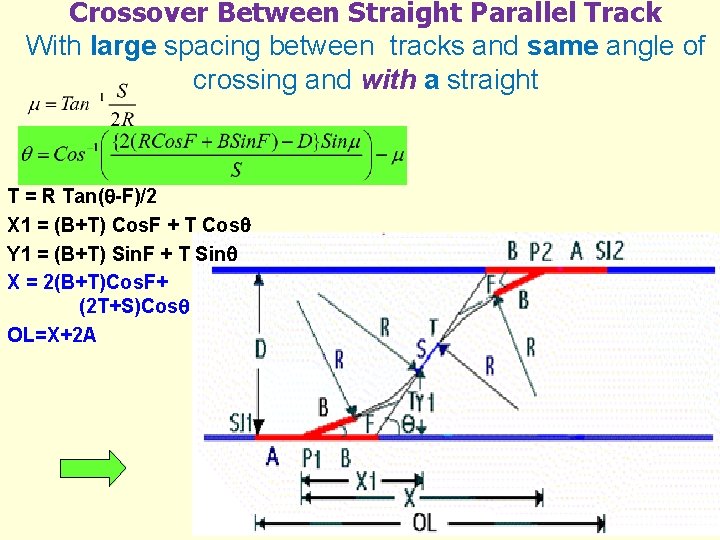
Crossover Between Straight Parallel Track With large spacing between tracks and same angle of crossing and with a straight T = R Tan( -F)/2 X 1 = (B+T) Cos. F + T Cos Y 1 = (B+T) Sin. F + T Sin X = 2(B+T)Cos. F+ (2 T+S)Cos OL=X+2 A

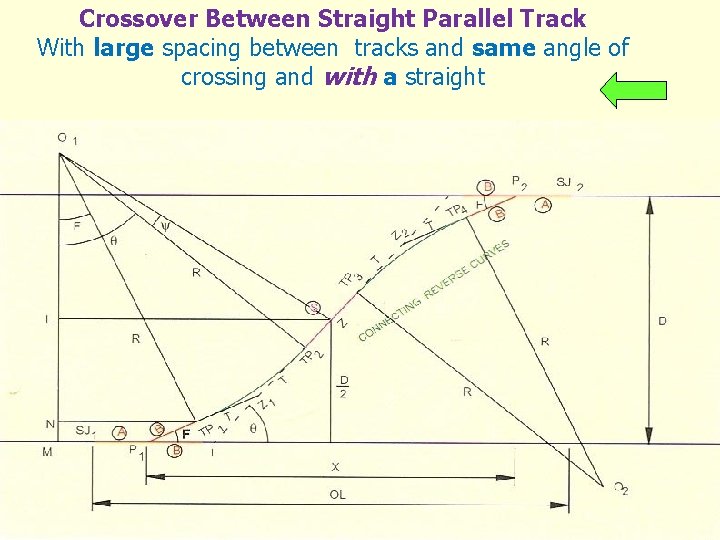
Crossover Between Straight Parallel Track With large spacing between tracks and same angle of crossing and with a straight

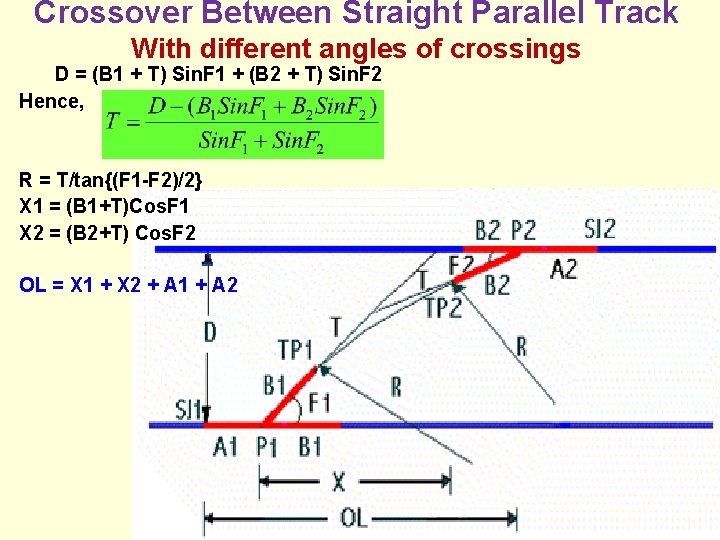
Crossover Between Straight Parallel Track With different angles of crossings D = (B 1 + T) Sin. F 1 + (B 2 + T) Sin. F 2 Hence, R = T/tan{(F 1 -F 2)/2} X 1 = (B 1+T)Cos. F 1 X 2 = (B 2+T) Cos. F 2 OL = X 1 + X 2 + A 1 + A 2

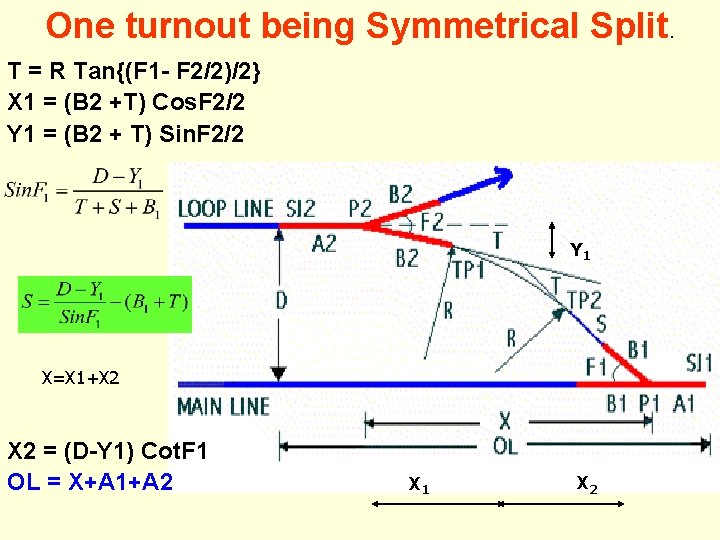
One turnout being Symmetrical Split. T = R Tan{(F 1 - F 2/2)/2} X 1 = (B 2 +T) Cos. F 2/2 Y 1 = (B 2 + T) Sin. F 2/2 Y 1 X=X 1+X 2 = (D-Y 1) Cot. F 1 OL = X+A 1+A 2 X 1 X 2

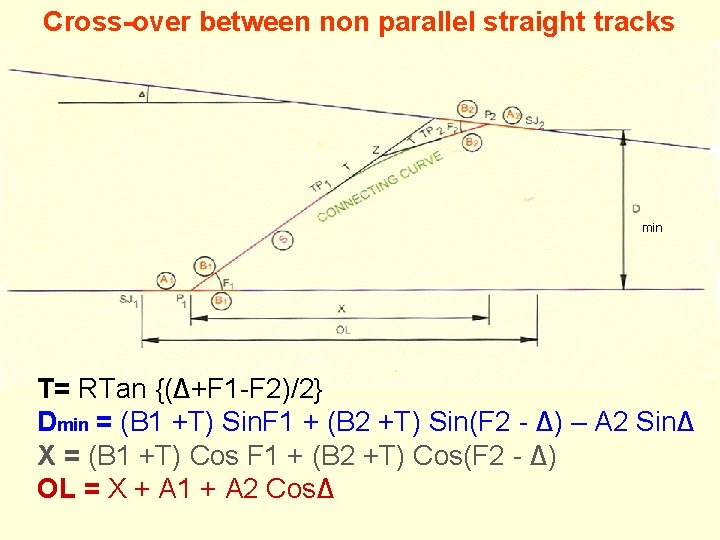
Cross-over between non parallel straight tracks min T= RTan {(Δ+F 1 -F 2)/2} Dmin = (B 1 +T) Sin. F 1 + (B 2 +T) Sin(F 2 - Δ) – A 2 SinΔ X = (B 1 +T) Cos F 1 + (B 2 +T) Cos(F 2 - Δ) OL = X + A 1 + A 2 CosΔ

Cross-over between non parallel straight tracks (I) Given - R, Δ, T/o parameters Find – T - (from eq. 1) Dmin (Location of SJ 2) - (from eq. 2), X - (from eq. 3), OL - (from eq. 4) (II) Given – D, Δ, T/o parameters Find – T - (from eq. 2), R - (from eq. 1) X - (from eq. 3), OL - (from eq. 4)

CONNECTION BETWEEN CURVED TRACK TO PARALLEL CURVED TRACK OR DIVERGENT STRAIGHT TRACK o Connection between two curved parallel tracks - connection on outside of main line curve without straight - connection on outside of main line curve with a straight - connection on inside of main line curve o Connection between a curved track to straight track - connection on inside of main line curve - connection on outside of main line

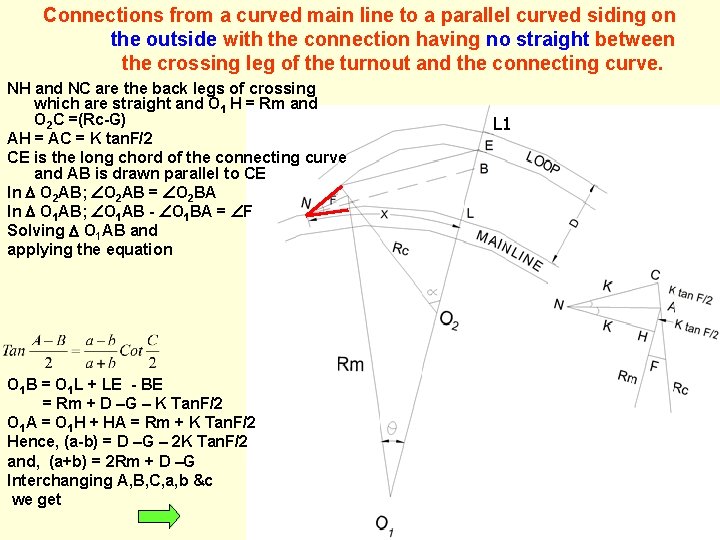
Connections from a curved main line to a parallel curved siding on the outside with the connection having no straight between the crossing leg of the turnout and the connecting curve. NH and NC are the back legs of crossing which are straight and O 1 H = Rm and O 2 C =(Rc-G) AH = AC = K tan. F/2 CE is the long chord of the connecting curve and AB is drawn parallel to CE In O 2 AB; O 2 AB = O 2 BA In O 1 AB; O 1 AB - O 1 BA = F Solving O 1 AB and applying the equation O 1 B = O 1 L + LE - BE = Rm + D –G – K Tan. F/2 O 1 A = O 1 H + HA = Rm + K Tan. F/2 Hence, (a-b) = D –G – 2 K Tan. F/2 and, (a+b) = 2 Rm + D –G Interchanging A, B, C, a, b &c we get L 1

In triangle O 1 AO 2 using formula Sin. A/a =Sin. B/b, we get X = NL = NH + HL = (Rx x /180) + K

• Crossing is fixed first in case of connection to curved tracks. • Distance ‘D’ between two curved parallel tracks & Radius of main line ‘Rm’ are known from field surveying. • Value of turnout parameters will be known once t/out is decided. • Angle ǿ & Radius of connecting curve ‘Rc’ are calculated. • Finally ‘X’ is calculated & ‘L’ & ‘L 1’are fixed wrt TNC.

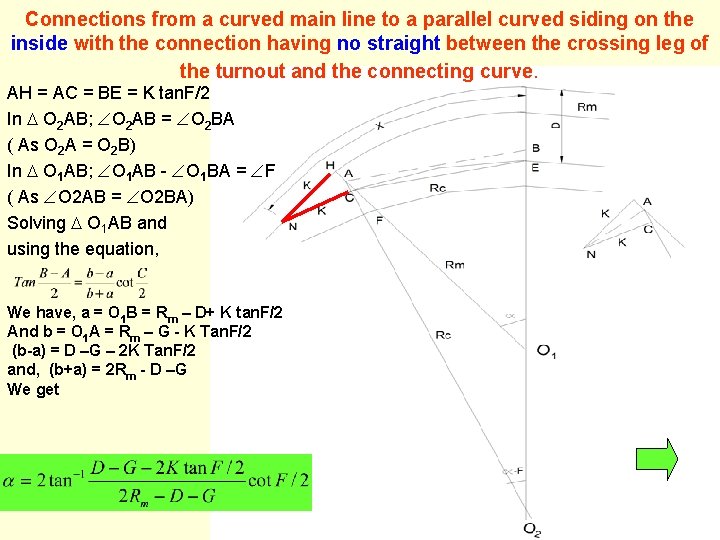
Connections from a curved main line to a parallel curved siding on the inside with the connection having no straight between the crossing leg of the turnout and the connecting curve. AH = AC = BE = K tan. F/2 In O 2 AB; O 2 AB = O 2 BA ( As O 2 A = O 2 B) In O 1 AB; O 1 AB - O 1 BA = F ( As O 2 AB = O 2 BA) Solving O 1 AB and using the equation, We have, a = O 1 B = Rm – D+ K tan. F/2 And b = O 1 A = Rm – G - K Tan. F/2 (b-a) = D –G – 2 K Tan. F/2 and, (b+a) = 2 Rm - D –G We get

Solving O 1 O 2 A and using equation We have, O 2 A = Rc + K tan(F/2) & O 1 A = Rm – G - K Tan. F/2, we get X = NL = NH + HL = (Rm-G)x x /180) + K Sin( -F) can have a positive, zero or a negative value as value of depends upon Rm and D other factors being constant. When ( -F) has a positive value, Rc is positive and the Rc and Rm are in similar flexures. When ( -F) is zero, Rc is infinite i. e. , the two are connected by straight line and when ( -F) has a negative value, Rc is in reverse flexures to the main line curve.

Cross-over between curved parallel tracks • • • In O 1 O 2 A, O 1 A = Rm + K Tan F/2 O 2 A = Rc –G - K Tan F/2 (O 1 O 2)2 = (O 1 A)2 + (O 2 A)2 - 2 O 1 A x. O 2 A Cos F = (Rm+KTan. F/2) 2+ (Rc-G-Ktan. F/2) 2 -2(Rm+KTan. F/2) (Rc-G-Ktan. F/2)Cos. F ………. . (1) In O 1 O 2 B, O 1 B = Rc + K Tan F/2 O 2 B = Rm –D-G - K Tan F/2 (O 1 O 2) 2 = O 1 B 2 + O 2 B 2 - 2 O 1 Bx O 2 B Cos F = (Rc+KTan. F/2) 2 +(Rm-D-G-Ktan. F/2) 2 2(Rc+KTan. F/2) (Rm-D-G-Ktan. F/2)Cos. F ………. . (2) Equating equations (1) & (2), We can have,

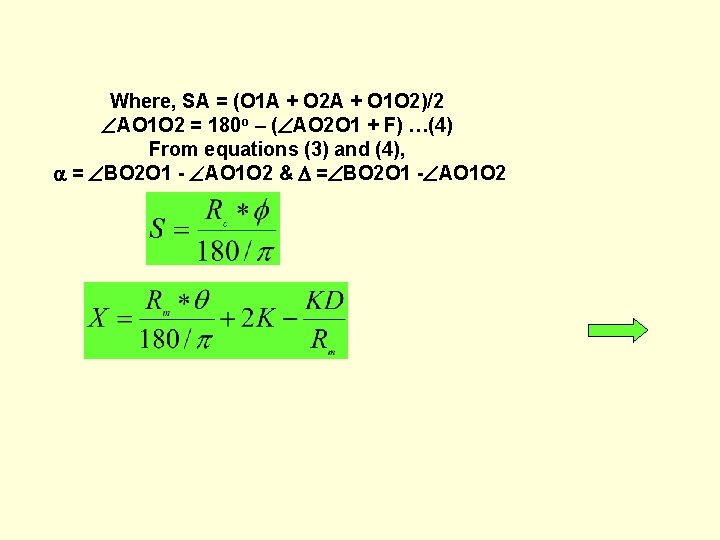
In O 1 O 2 B, O 1 B = Rc + K Tan F/2 O 2 B = Rm –D-G - K Tan F/2 (O 1 O 2)2 = OB 12 + OB 22 - 2 O 1 Bx O 2 B Cos O 1 BO 2 Where, SB = (O 1 B + O 2 B + O 1 O 2)/2 BO 2 O 1 = 180 o – ( BO 1 O 2 + F). (3) In O 1 O 2 A, O 1 A = Rm + K Tan F/2 O 2 A = Rc –G - K Tan F/2 (O 1 O 2)2 = OA 12 + OA 22 - 2 O 1 A x. O 2 A Cos O 1 AO 2

Where, SA = (O 1 A + O 2 A + O 1 O 2)/2 AO 1 O 2 = 180 o – ( AO 2 O 1 + F) …(4) From equations (3) and (4), = BO 2 O 1 - AO 1 O 2 & = BO 2 O 1 - AO 1 O 2

GATHERING LINES OR LADDER

Gathering line laid at angle of crossing This is the simplest and most commonly adopted layout for a gathering line specially in a passenger yard. In this layout, distance P 0 – P 1, P 1 – P 2, P 2 – P 3 are equal and this distance ‘LL’ is greater than the overall length of turnout. The best method to lay a gathering line is by co-ordinates of the deflection points with reference to the 1 st deflection point Po as origin. P 3 P 2 P 1 F

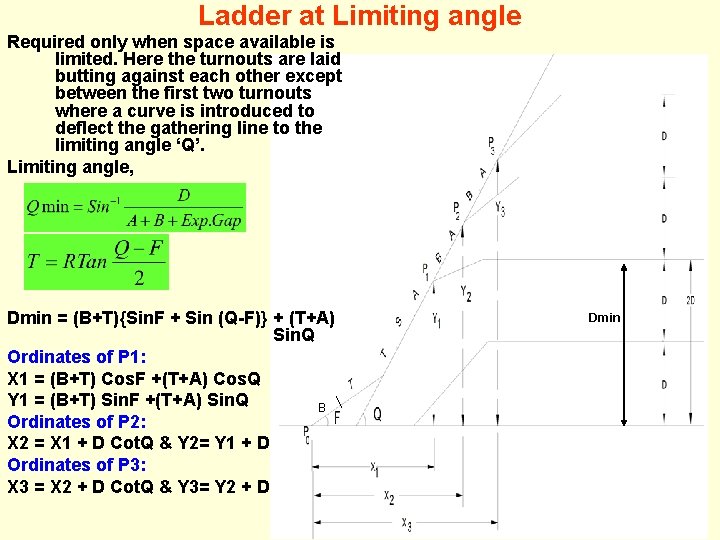
Ladder at Limiting angle Required only when space available is limited. Here the turnouts are laid butting against each other except between the first two turnouts where a curve is introduced to deflect the gathering line to the limiting angle ‘Q’. Limiting angle, Dmin = (B+T){Sin. F + Sin (Q-F)} + (T+A) Sin. Q Ordinates of P 1: X 1 = (B+T) Cos. F +(T+A) Cos. Q Y 1 = (B+T) Sin. F +(T+A) Sin. Q B Ordinates of P 2: X 2 = X 1 + D Cot. Q & Y 2= Y 1 + D Ordinates of P 3: X 3 = X 2 + D Cot. Q & Y 3= Y 2 + D Dmin

T/Os taking off from curved tracks Dt=Ds+Dm Similar flexure

T/Os taking off from curved tracks Dt=Ds-Dm Contrary Flexure

T/Os taking off from curved tracks Dt = Dm Symmetrical split