Lawrence Livermore National Laboratory Using surrogate nuclear reactions

Lawrence Livermore National Laboratory Using surrogate nuclear reactions to determine (n, f) and (n, g) cross sections August 8, 2009 Nicholas Scielzo Physics Division, Physical and Life Sciences Lawrence Livermore National Laboratory, P. O. Box 808, Livermore, CA 94551 This work performed under the auspices of the U. S. Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC 52 -07 NA 27344 LLNL-PRES-408002

Surrogate Nuclear Reactions Approach The Surrogate Nuclear Reactions approach is an indirect method for determining cross sections of compound-nuclear reactions Used when direct measurements are not possible because of beam and/or target limitations – create compound nucleus through reaction of light-ion beam on a (more) stable isotope Can be used in regular or inverse kinematics Lawrence Livermore National Laboratory 2

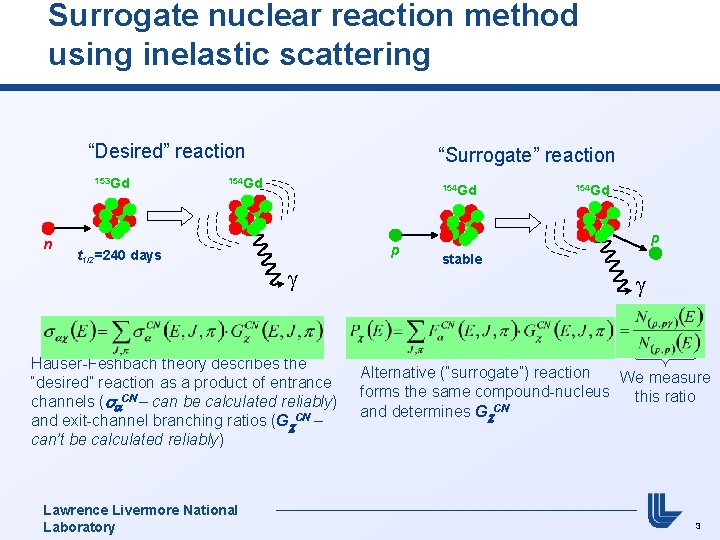
Surrogate nuclear reaction method using inelastic scattering “Desired” reaction 153 Gd n “Surrogate” reaction 154 Gd t 1/2=240 days 154 Gd p Hauser-Feshbach theory describes the “desired” reaction as a product of entrance channels (sa. CN – can be calculated reliably) and exit-channel branching ratios (Gc. CN – can’t be calculated reliably) Lawrence Livermore National Laboratory 154 Gd p stable Alternative (“surrogate”) reaction We measure forms the same compound-nucleus this ratio CN and determines Gc 3

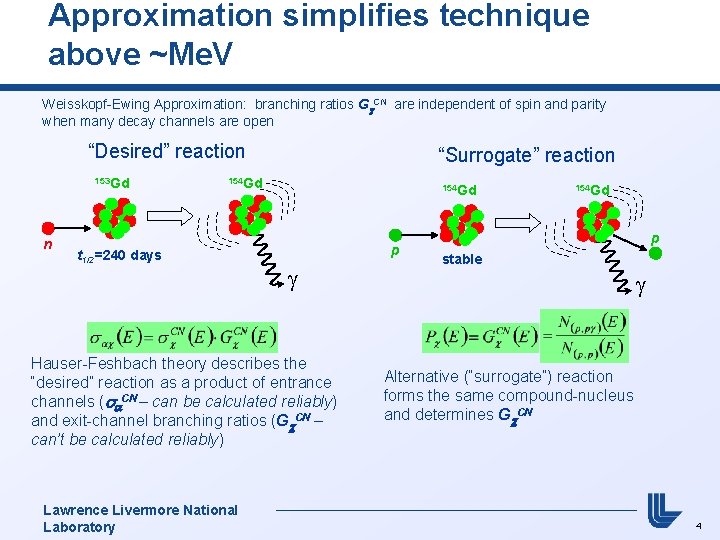
Approximation simplifies technique above ~Me. V Weisskopf-Ewing Approximation: branching ratios Gc. CN are independent of spin and parity when many decay channels are open “Desired” reaction 153 Gd n “Surrogate” reaction 154 Gd t 1/2=240 days 154 Gd p Hauser-Feshbach theory describes the “desired” reaction as a product of entrance channels (sa. CN – can be calculated reliably) and exit-channel branching ratios (Gc. CN – can’t be calculated reliably) Lawrence Livermore National Laboratory 154 Gd p stable Alternative (“surrogate”) reaction forms the same compound-nucleus and determines Gc. CN 4

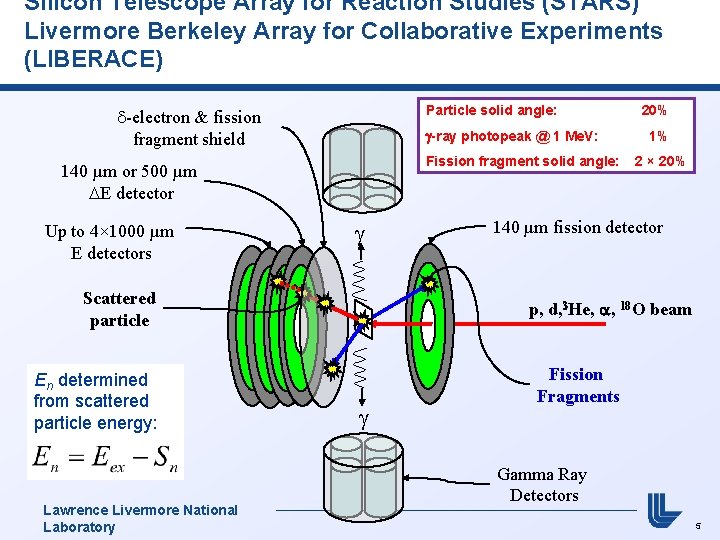
Silicon Telescope Array for Reaction Studies (STARS) Livermore Berkeley Array for Collaborative Experiments (LIBERACE) Particle solid angle: d-electron & fission fragment shield g-ray photopeak @ 1 Me. V: Fission fragment solid angle: 140 µm or 500 µm E detector Up to 4× 1000 µm E detectors Scattered particle En determined from scattered particle energy: Lawrence Livermore National Laboratory 20% 1% 2 × 20% 140 µm fission detector p, d, He, , 18 O beam Fission Fragments Gamma Ray Detectors 5

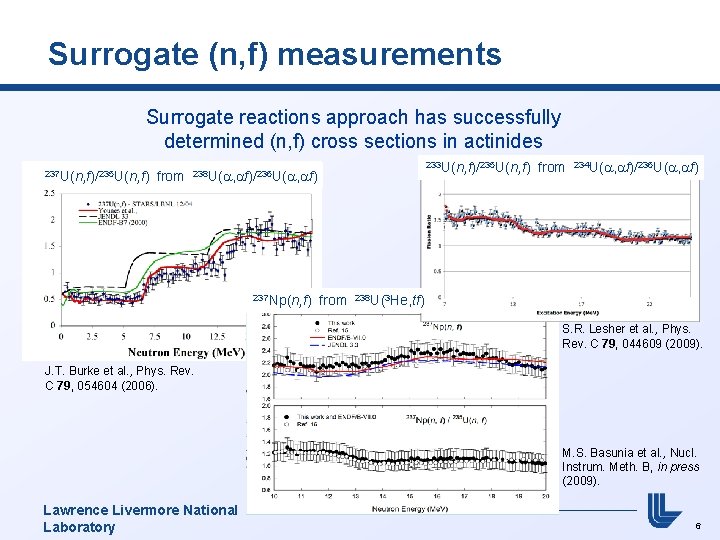
Surrogate (n, f) measurements Surrogate reactions approach has successfully determined (n, f) cross sections in actinides 237 U(n, f)/235 U(n, f) from 233 U(n, f)/235 U(n, f) 238 U(a, af)/236 U(a, af) 237 Np(n, f) from 234 U(a, af)/236 U(a, af) 238 U(3 He, tf) S. R. Lesher et al. , Phys. Rev. C 79, 044609 (2009). J. T. Burke et al. , Phys. Rev. C 79, 054604 (2006). M. S. Basunia et al. , Nucl. Instrum. Meth. B, in press (2009). Lawrence Livermore National Laboratory 6

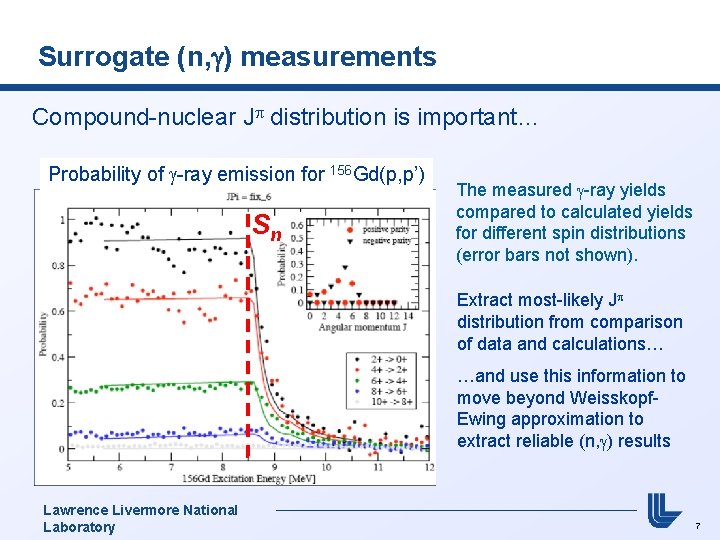
Surrogate (n, g) measurements Compound-nuclear Jp distribution is important… Probability of -ray emission for 156 Gd(p, p’) Sn The measured -ray yields compared to calculated yields for different spin distributions (error bars not shown). Extract most-likely Jp distribution from comparison of data and calculations… …and use this information to move beyond Weisskopf. Ewing approximation to extract reliable (n, ) results Lawrence Livermore National Laboratory 7

Requirements Experiments benefit from: § up to nano-Amp beams (regular or inverse kinematics) § light-ion reactions § efficient particle detectors with excellent PID and energy resolution § high-efficiency -ray detector arrays Lawrence Livermore National Laboratory 8

Collaborators Lawrence Livermore National Laboratory L. A. Bernstein, D. L. Bleuel, J. T. Burke, F. Dietrich, J. Escher, S. R. Lesher, E. B. Norman, N. D. Scielzo, S. Sheets, I. Thompson, M. Wiedeking U. C. Berkeley and Lawrence Berkeley National Laboratory M. S. Basunia, R. M. Clark, P. Fallon, J. Gibelin, R. Hatarik, B. Lyles, M. A. Mc. Mahan, L. Moretto, E. B. Norman, L. Phair, S. G. Prussin, E. Rodriguez-Vieitez University of Richmond J. M. Allmond, C. Beausang Rutgers University J. A. Cizewski, R. Hatarik, P. D. O’Malley and T. Swan Lawrence Livermore National Laboratory 9