Lattice design study for diffractionlimited storage rings Zhenghe

Lattice design study for diffraction-limited storage rings Zhenghe Bai (白正贺) NSRL, USTC Workshop of Measurement and Control Technology for Accelerator of Super Tau-Charm Facility USTC, Hefei 26 -27, June 2019

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

Diffraction-limited storage ring • Diffraction-limited storage ring (DLSR): the electron beam emittance approaches the diffraction-limited emittance λ/4π. • Multi-bend achromat (MBA) lattices are adopted in DLSR designs to reduce the emittance. • The first DLSR, MAX IV: emittance of ~300 pm·rad@3. 0 Ge. V. MAX IV 7 BA lattice

From Super. B lattice to Hybrid MBA lattice • Today many DLSR designs are based on the hybrid MBA lattice and its modifications. • The Hybrid MBA lattice proposed by ESRF EBS origins from the Super. B ARCs design. ESRF EBS lattice Super. B ARC lattice

Hybrid MBA lattice • Hybrid MBA lattice concept proposed by ESRF EBS: • Longitudinal and transverse gradient bends are used to reduce the emittance; • One pair of dispersion bumps separated by –I transformation are created for accommodating sextupoles so as to minimize nonlinear dynamics effects. ESRF EBS lattice

Motivation of our lattice study • The hybrid MBA lattice can promise both lower emittance and larger dynamic aperture. However, for DLSR designs with emittances of tens of pm·rad, it is difficult to achieve a large momentum aperture, and the amplitude dependent tune shift is also large. This is due to that the number of knobs for nonlinear dynamics optimization is limited in the hybrid MBA lattice. 1. Can we propose other new lattice concepts to achieve both larger dynamic aperture and larger momentum aperture? 2. Can we develop a new method for hybrid MBA lattice design to search for better nonlinear dynamics results?

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

Locally symmetric MBA • The locally symmetric MBA (LS-MBA) lattice concept: • The horizontal and vertical beta functions of each lattice cell are made to be locally symmetric about two mirror planes, which have the same distance from the midplane of the cell. • The horizontal and vertical phase advances between the two mirror planes satisfy: μx = (2 m+1)π, μy = nπ , where m & n are integers. Zhenghe Bai, et al. , in: Proc. IPAC 2017

Locally symmetric MBA • From the concept, we can deduce the following: • The local symmetry indicates an invariance: the transfer map from any point in [A, B] to its corresponding point in [B, C] is the same. • Many nonlinear dynamics effects caused by normal sextupoles located in the locally symmetric region can be naturally cancelled out within one lattice cell. • There can be many families of sextupoles in one lattice cell, which can be employed to control, for example, high-order resonance driving terms, tune shifts with amplitude and tune shifts with momentum. Note that harmonic sextupoles can be included.

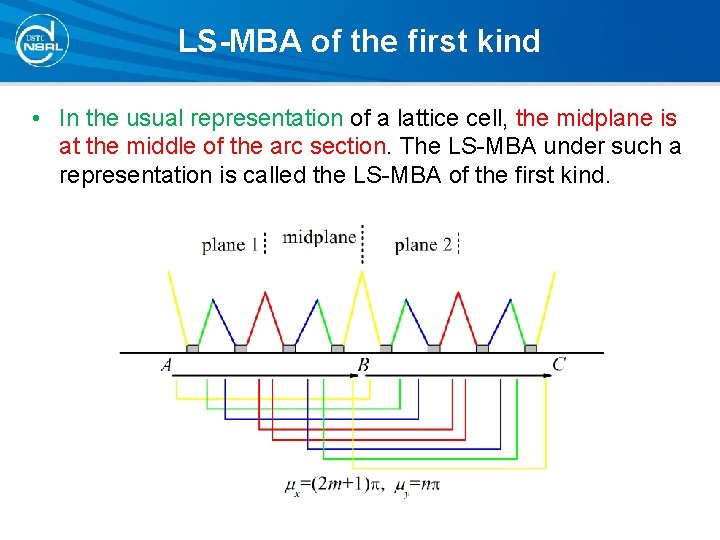
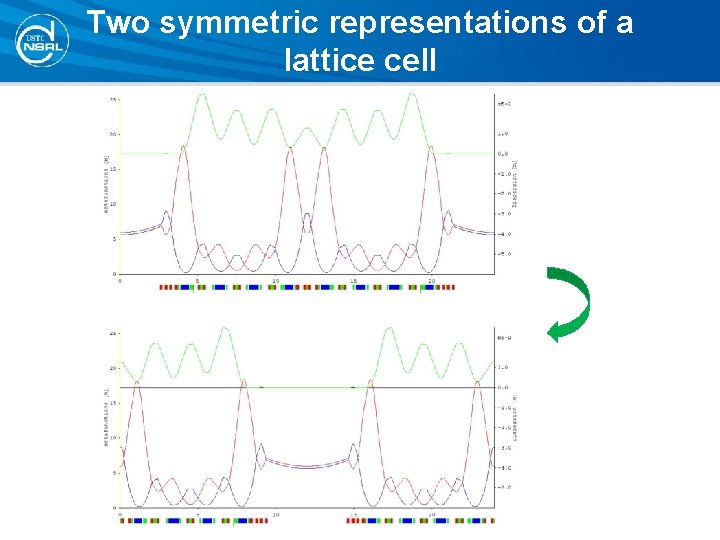
LS-MBA of the first kind • In the usual representation of a lattice cell, the midplane is at the middle of the arc section. The LS-MBA under such a representation is called the LS-MBA of the first kind.

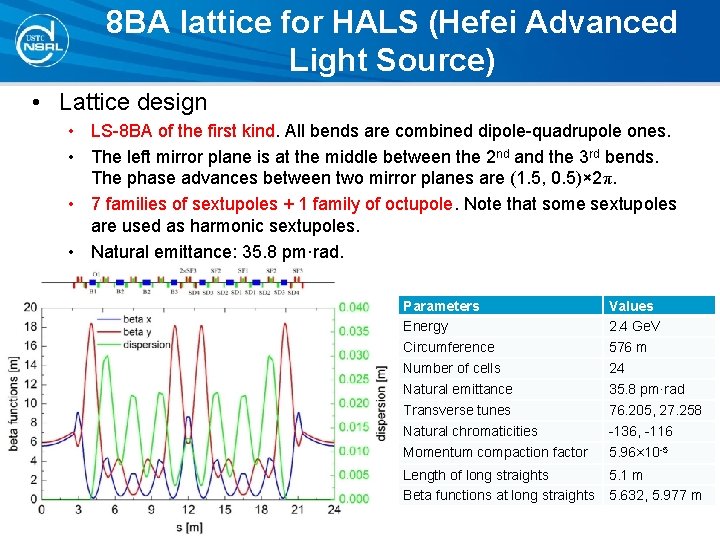
8 BA lattice for HALS (Hefei Advanced Light Source) • Lattice design • LS-8 BA of the first kind. All bends are combined dipole-quadrupole ones. • The left mirror plane is at the middle between the 2 nd and the 3 rd bends. The phase advances between two mirror planes are (1. 5, 0. 5)× 2π. • 7 families of sextupoles + 1 family of octupole. Note that some sextupoles are used as harmonic sextupoles. • Natural emittance: 35. 8 pm·rad. Parameters Energy Circumference Number of cells Natural emittance Transverse tunes Natural chromaticities Momentum compaction factor Values 2. 4 Ge. V 576 m 24 35. 8 pm·rad 76. 205, 27. 258 -136, -116 5. 96× 10 -5 Length of long straights Beta functions at long straights 5. 1 m 5. 632, 5. 977 m

8 BA lattice for HALS • Nonlinear dynamics optimization: • Dynamic aperture (DA): ~ 150 sigma (sigma: rms beam size). Only the part of the DA with y below 1. 5 mm is shown in the figure. • The amplitude dependent tunes are controlled in a relatively small tune region. Note that DA can be further optimized by grouping sextupoles into more families.

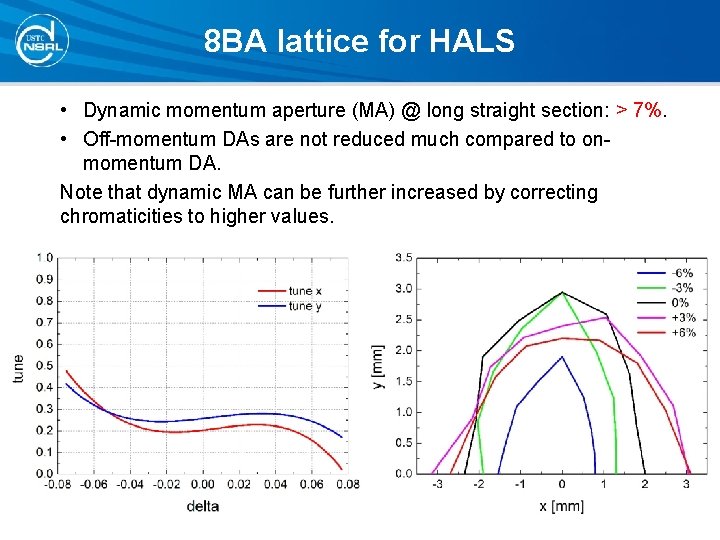
8 BA lattice for HALS • Dynamic momentum aperture (MA) @ long straight section: > 7%. • Off-momentum DAs are not reduced much compared to onmomentum DA. Note that dynamic MA can be further increased by correcting chromaticities to higher values.

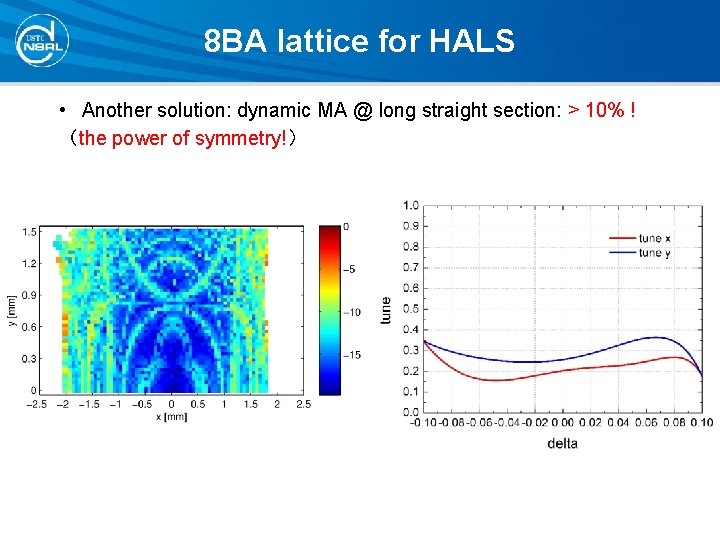
8 BA lattice for HALS • Another solution: dynamic MA @ long straight section: > 10% ! （the power of symmetry!）

Two symmetric representations of a lattice cell

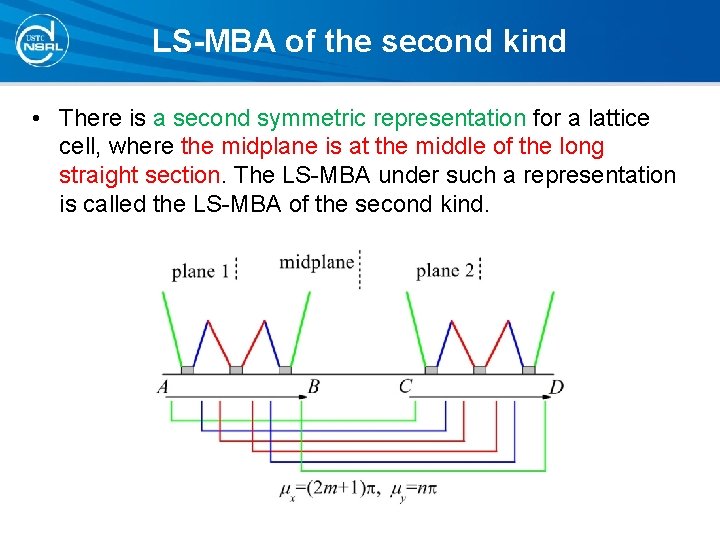
LS-MBA of the second kind • There is a second symmetric representation for a lattice cell, where the midplane is at the middle of the long straight section. The LS-MBA under such a representation is called the LS-MBA of the second kind.

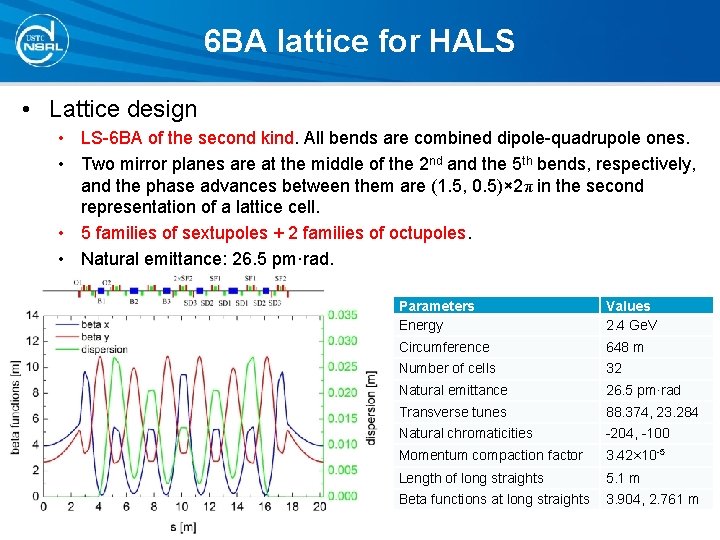
6 BA lattice for HALS • Lattice design • LS-6 BA of the second kind. All bends are combined dipole-quadrupole ones. • Two mirror planes are at the middle of the 2 nd and the 5 th bends, respectively, and the phase advances between them are (1. 5, 0. 5)× 2π in the second representation of a lattice cell. • 5 families of sextupoles + 2 families of octupoles. • Natural emittance: 26. 5 pm·rad. Parameters Energy Values 2. 4 Ge. V Circumference 648 m Number of cells 32 Natural emittance 26. 5 pm·rad Transverse tunes 88. 374, 23. 284 Natural chromaticities -204, -100 Momentum compaction factor 3. 42× 10 -5 Length of long straights 5. 1 m Beta functions at long straights 3. 904, 2. 761 m

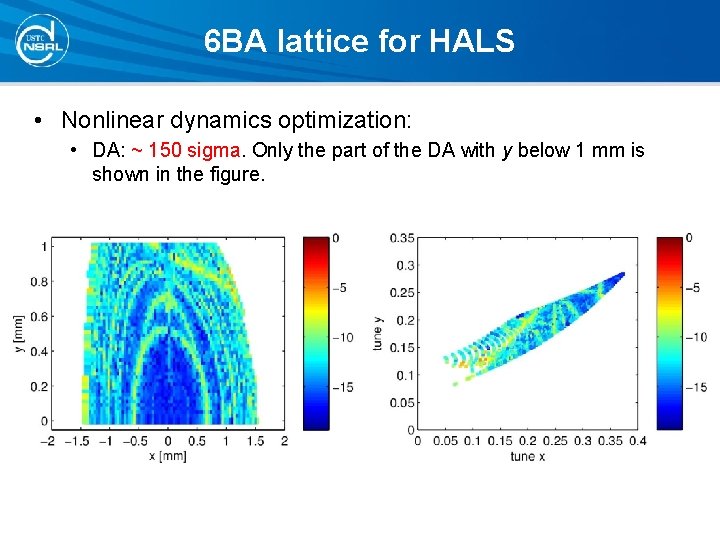
6 BA lattice for HALS • Nonlinear dynamics optimization: • DA: ~ 150 sigma. Only the part of the DA with y below 1 mm is shown in the figure.

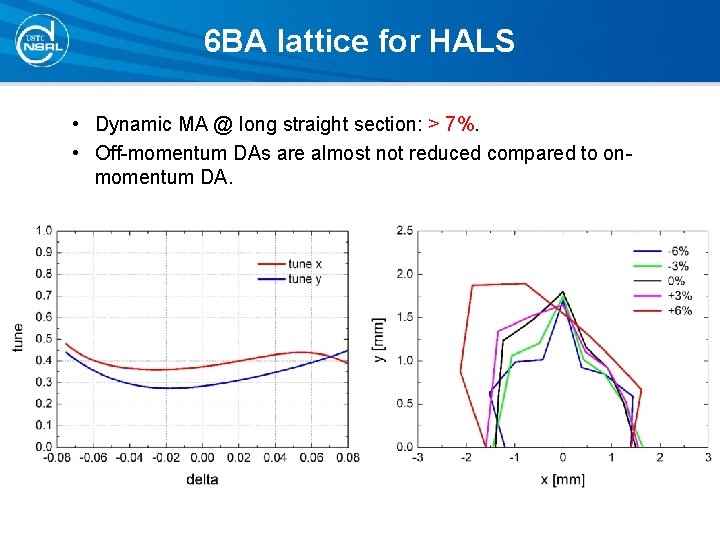
6 BA lattice for HALS • Dynamic MA @ long straight section: > 7%. • Off-momentum DAs are almost not reduced compared to onmomentum DA.

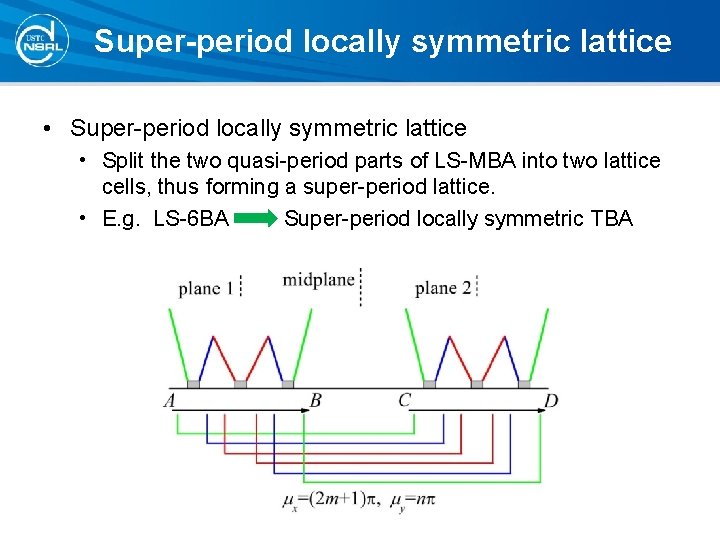
Super-period locally symmetric lattice • Split the two quasi-period parts of LS-MBA into two lattice cells, thus forming a super-period lattice. • E. g. LS-6 BA Super-period locally symmetric TBA

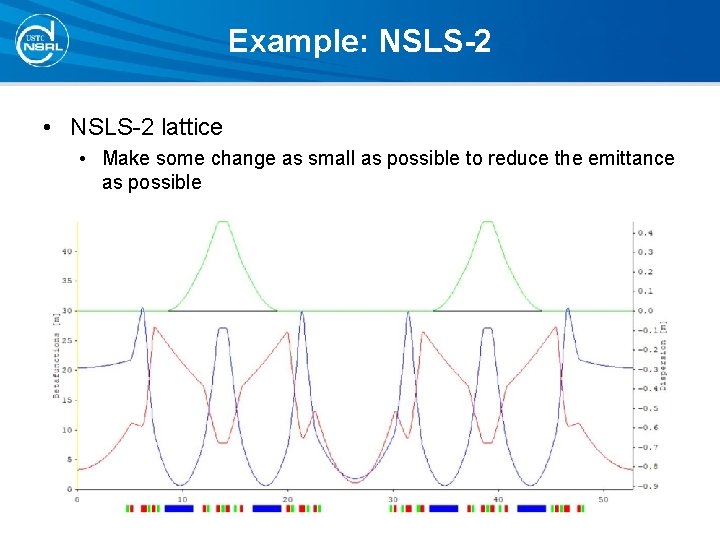
Example: NSLS-2 • NSLS-2 lattice • Make some change as small as possible to reduce the emittance as possible

Example: NSLS-2 • Lower-emittance lattice study for NSLS-2 • Super-period locally symmetric TBA • The natural emittance is lowered from 2. 1 nm·rad down to 0. 3 nm·rad (7 times!). Zhenghe Bai, Yongjun Li (BNL), Oct. , 2018

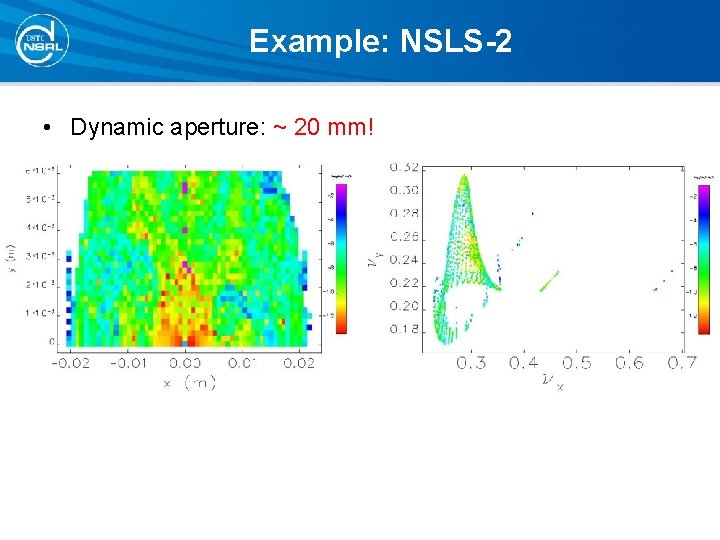
Example: NSLS-2 • Dynamic aperture: ~ 20 mm!

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

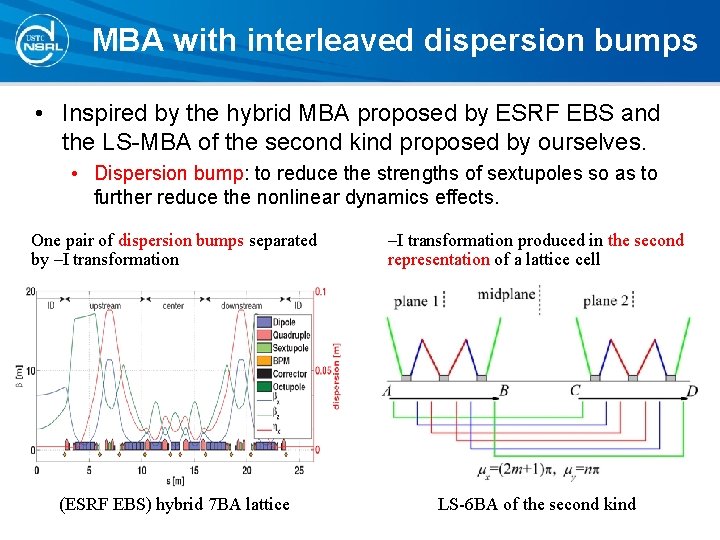
MBA with interleaved dispersion bumps • Inspired by the hybrid MBA proposed by ESRF EBS and the LS-MBA of the second kind proposed by ourselves. • Dispersion bump: to reduce the strengths of sextupoles so as to further reduce the nonlinear dynamics effects. One pair of dispersion bumps separated by –I transformation produced in the second representation of a lattice cell (ESRF EBS) hybrid 7 BA lattice LS-6 BA of the second kind

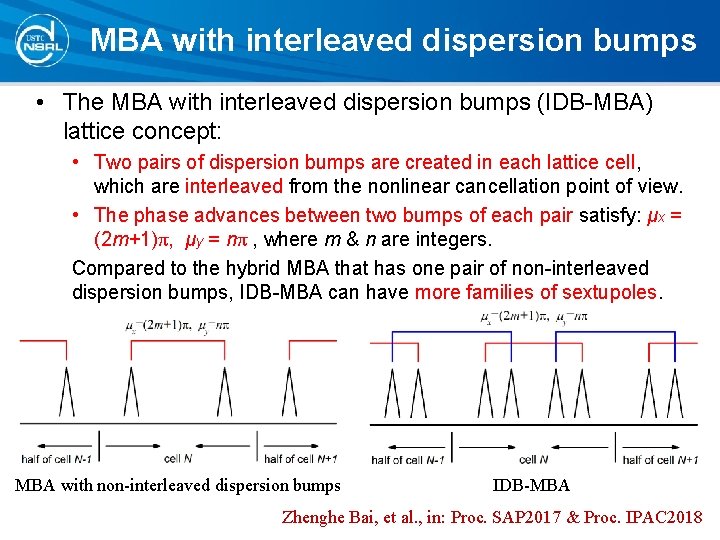
MBA with interleaved dispersion bumps • The MBA with interleaved dispersion bumps (IDB-MBA) lattice concept: • Two pairs of dispersion bumps are created in each lattice cell, which are interleaved from the nonlinear cancellation point of view. • The phase advances between two bumps of each pair satisfy: μx = (2 m+1)π, μy = nπ , where m & n are integers. Compared to the hybrid MBA that has one pair of non-interleaved dispersion bumps, IDB-MBA can have more families of sextupoles. MBA with non-interleaved dispersion bumps IDB-MBA Zhenghe Bai, et al. , in: Proc. SAP 2017 & Proc. IPAC 2018

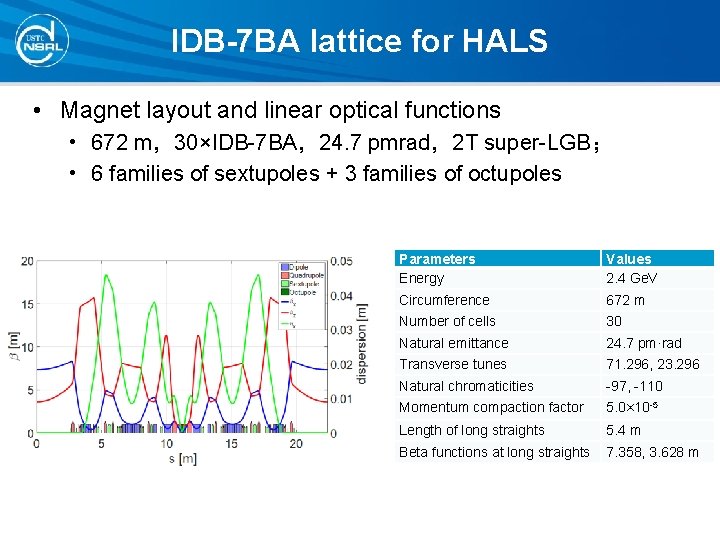
IDB-7 BA lattice for HALS • Magnet layout and linear optical functions • 672 m，30×IDB-7 BA，24. 7 pmrad，2 T super-LGB； • 6 families of sextupoles + 3 families of octupoles Parameters Energy Values 2. 4 Ge. V Circumference 672 m Number of cells 30 Natural emittance 24. 7 pm·rad Transverse tunes 71. 296, 23. 296 Natural chromaticities -97, -110 Momentum compaction factor 5. 0× 10 -5 Length of long straights 5. 4 m Beta functions at long straights 7. 358, 3. 628 m

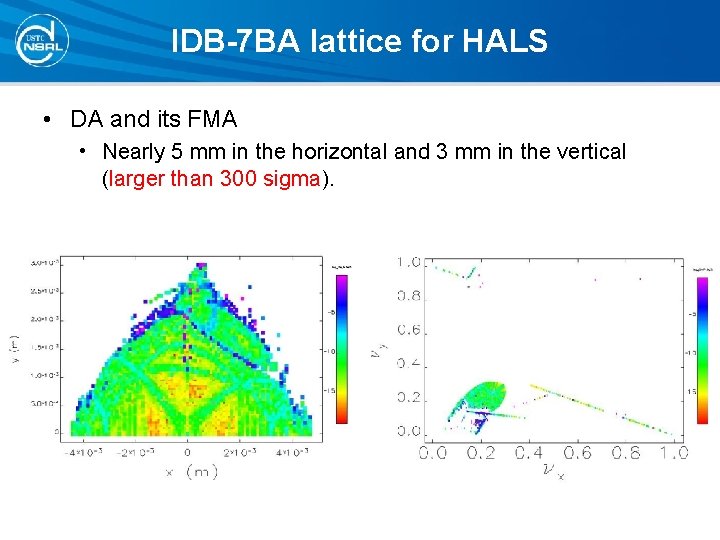
IDB-7 BA lattice for HALS • DA and its FMA • Nearly 5 mm in the horizontal and 3 mm in the vertical (larger than 300 sigma).

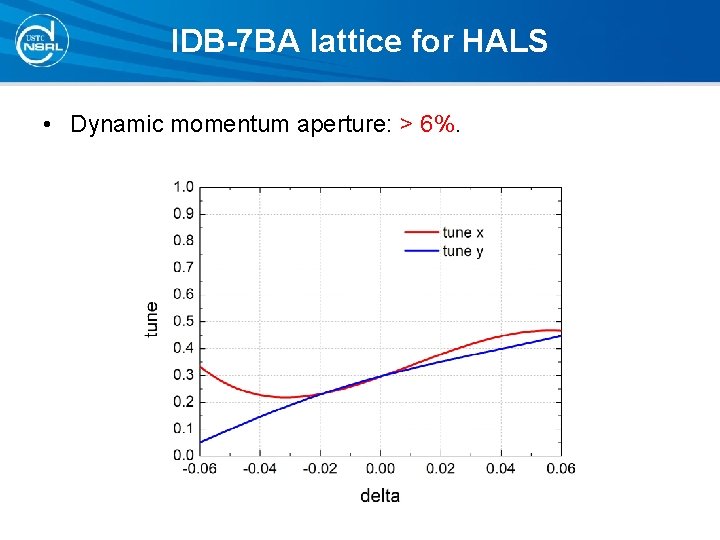
IDB-7 BA lattice for HALS • Dynamic momentum aperture: > 6%.

IDB-7 BA lattice for HALS • Off-momentum DAs are also large.

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

Method • A new method for designing hybrid MBA lattice • Linear lattice design using MOGA / MOPSO • 3 objective functions (including nonlinear dynamics indicators): • Natural emittance (or radiation brightness) • Sum of absolute values of natural chromaticities • Sum of absolute integral strengths of sextupoles – 3 families of sextupoles as a combination of (SF, SD 1) and (SF, SD 2); – Contribution of (SF, SD 1) to chromaticity correction: 2/3, (SF, SD 2): 1/3. • Physics behind the method • To Minimize nonlinear driving terms by optimizing nonlinear dynamics indicators Penghui Yang, Zhenghe Bai, et al. , in: Proc. IPAC 2019

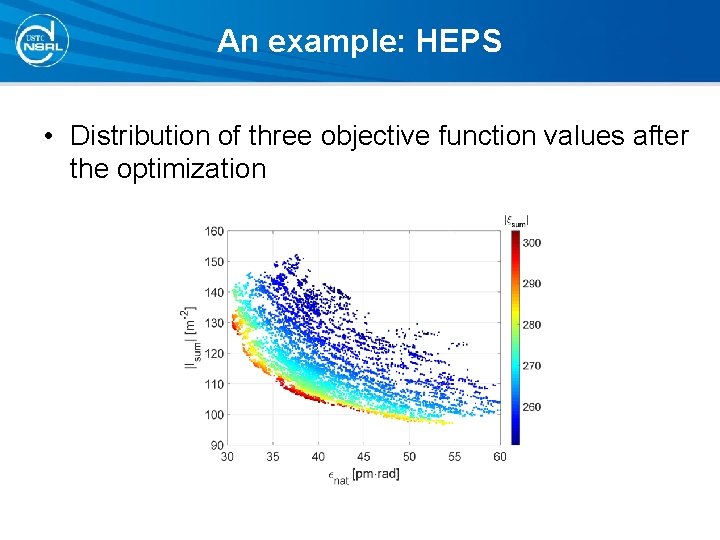
An example: HEPS • Distribution of three objective function values after the optimization

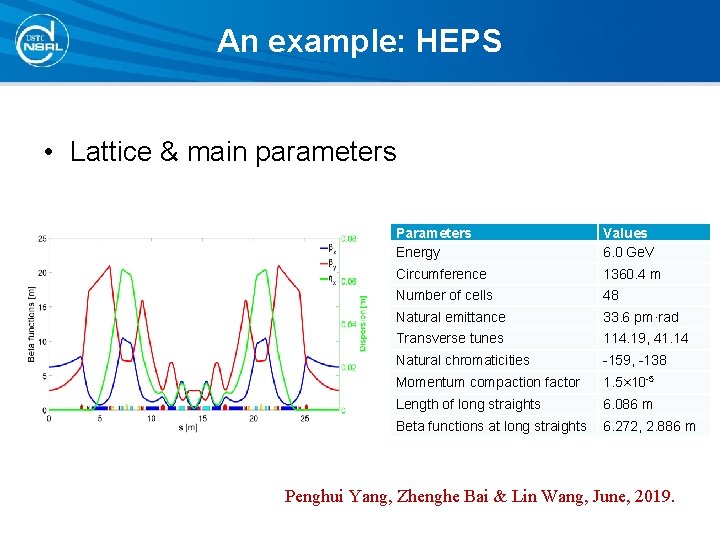
An example: HEPS • Lattice & main parameters Parameters Energy Values 6. 0 Ge. V Circumference 1360. 4 m Number of cells 48 Natural emittance 33. 6 pm·rad Transverse tunes 114. 19, 41. 14 Natural chromaticities -159, -138 Momentum compaction factor 1. 5× 10 -5 Length of long straights 6. 086 m Beta functions at long straights 6. 272, 2. 886 m Penghui Yang, Zhenghe Bai & Lin Wang, June, 2019.

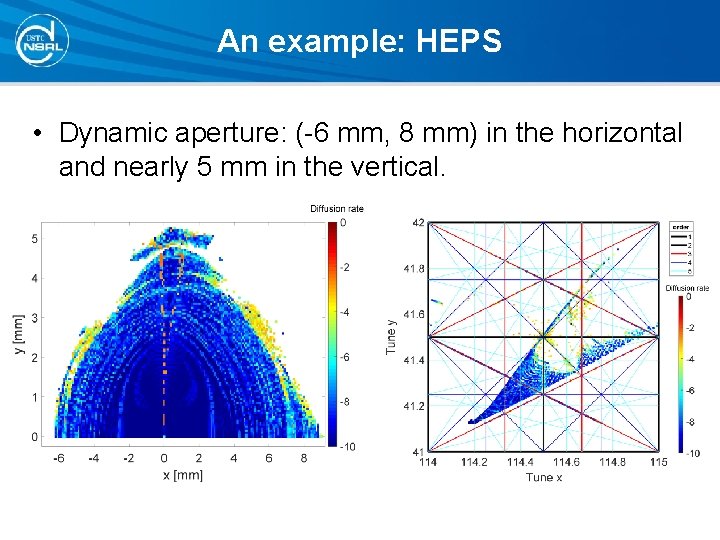
An example: HEPS • Dynamic aperture: (-6 mm, 8 mm) in the horizontal and nearly 5 mm in the vertical.

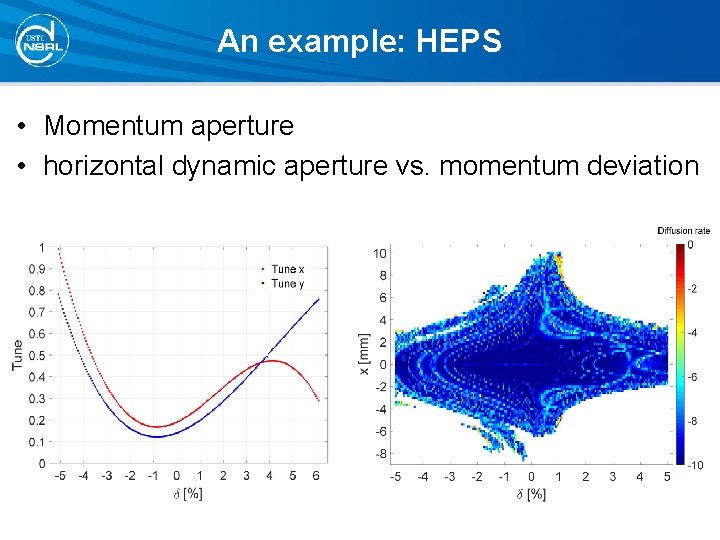
An example: HEPS • Momentum aperture • horizontal dynamic aperture vs. momentum deviation

Outline Ø Introduction Ø Locally symmetric lattices Ø MBA lattice with interleaved dispersion bumps Ø A new method for hybrid MBA lattice design Ø Conclusion and outlook

Conclusion and outlook • Locally symmetric lattice and IDB-MBA lattice concepts have been proposed and applied in the designs of HALS and possible NSLS-2 upgrade. Both larger DA and larger MA can be obtained. • A new method for designing hybrid MBA lattice has just been proposed, and its application in the design of HEPS showed the power of this method. • These lattice concepts and method could find their possible applications in the designs of colliders and other types of accelerators.

Thank you for your attention!