LatinAmerican on Theoretical Informatics Symposium LATIN 2008 Paths

Latin-American on Theoretical Informatics Symposium LATIN 2008 Paths and Trails in Edge Colored Graphs Abouelaoualim, K. Das, L. Faria, Y. Manoussakis, C. Martinhon, R. Saad Buzios-RJ - Brazil

Topics 1. Motivation and basic definitions 2. Properly edge-colored s-t path/trail and extensions 3. NP-completeness 4. Approximation Algorithms for associated maximization problems 5. Some instances solved in polynomial time 6. Conclusions and open problems

Some Applications using edge colored graphs 1. Computational Biology when the colors are used to denote a sequence of chromosomes; 2. Cryptography when a color specify a type of transmission; 3. Social Sciences where a color represents a relation between 2 individuals; etc

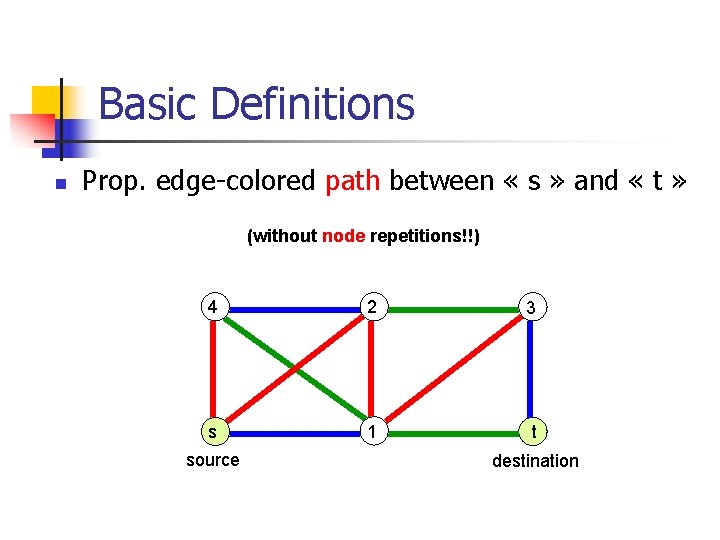
Basic Definitions n Prop. edge-colored path between « s » and « t » (without node repetitions!!) 4 2 3 s 1 t source destination

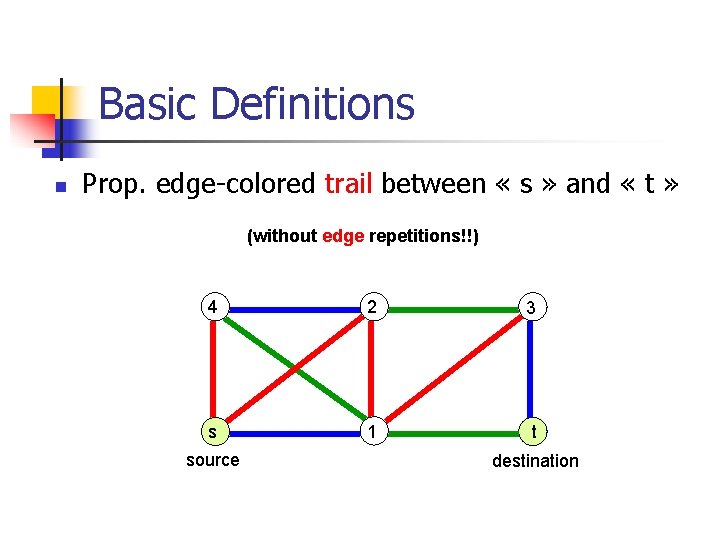
Basic Definitions n Prop. edge-colored trail between « s » and « t » (without edge repetitions!!) 4 2 3 s 1 t source destination

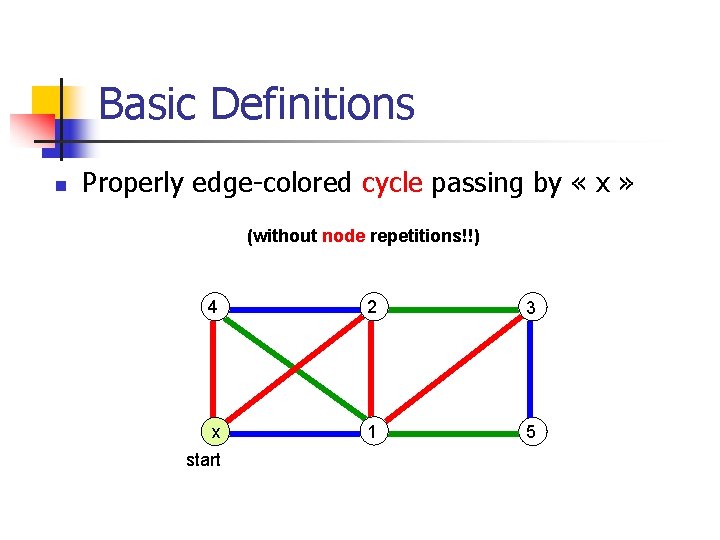
Basic Definitions n Properly edge-colored cycle passing by « x » (without node repetitions!!) 4 2 3 x 1 5 start

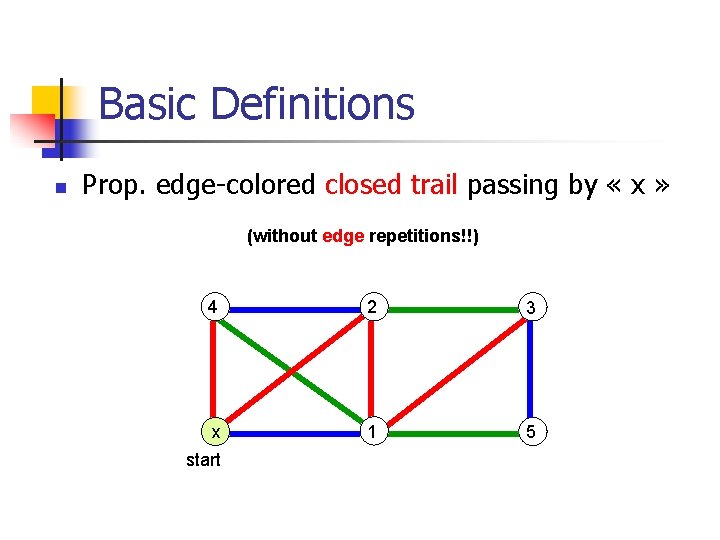
Basic Definitions n Prop. edge-colored closed trail passing by « x » (without edge repetitions!!) 4 2 3 x 1 5 start

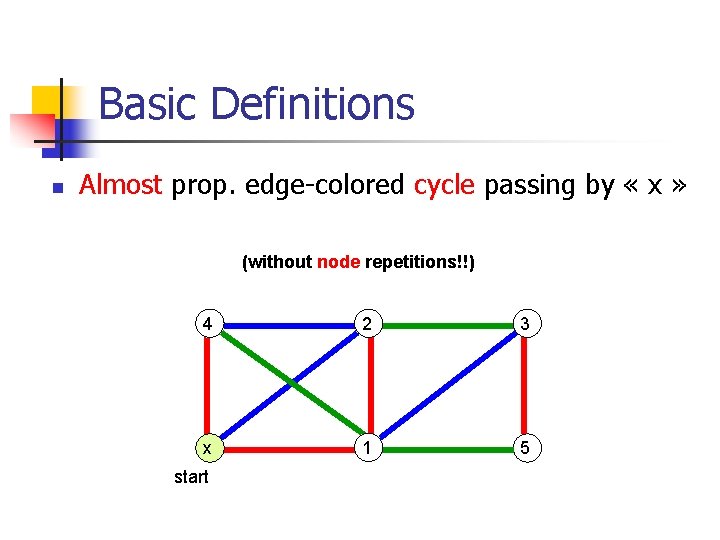
Basic Definitions n Almost prop. edge-colored cycle passing by « x » (without node repetitions!!) 4 2 3 x 1 5 start

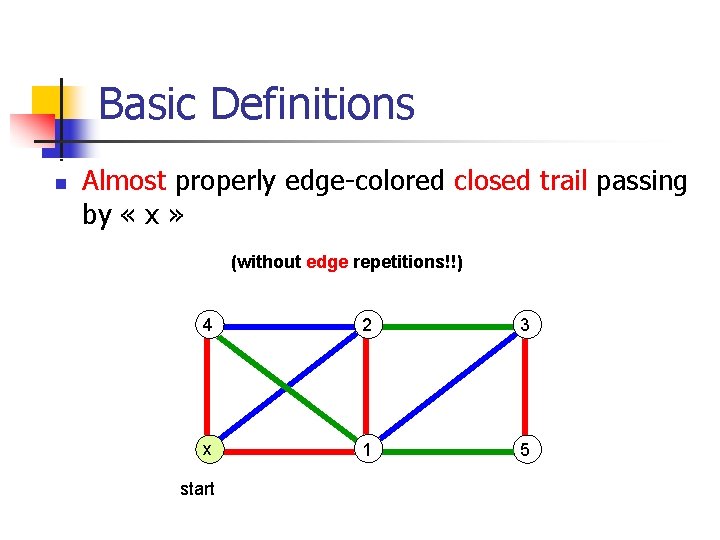
Basic Definitions n Almost properly edge-colored closed trail passing by « x » (without edge repetitions!!) 4 2 3 x 1 5 start

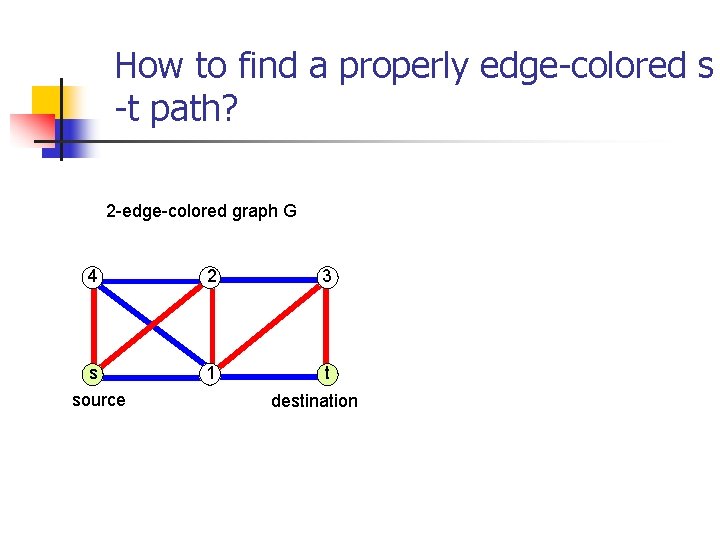
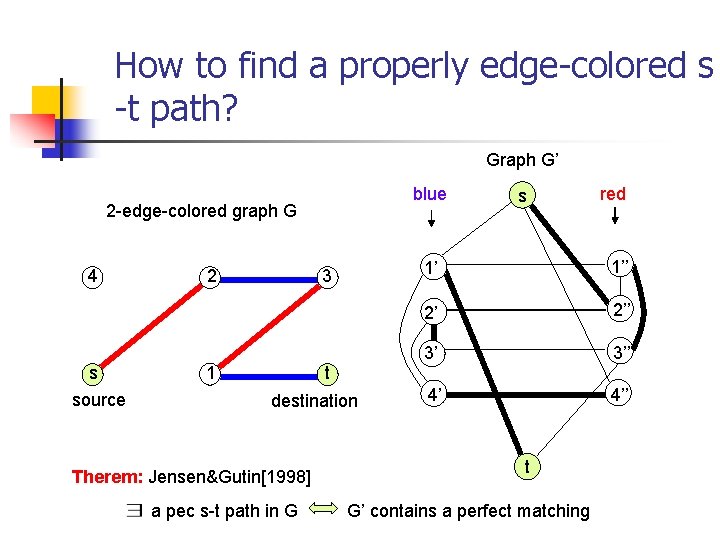
How to find a properly edge-colored s -t path? 2 -edge-colored graph G 4 2 3 s 1 t source destination

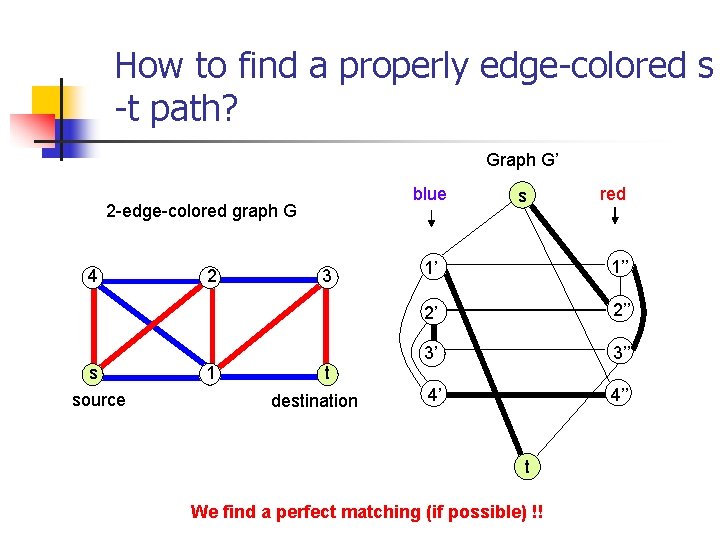
How to find a properly edge-colored s -t path? Graph G’ blue 2 -edge-colored graph G 4 s source 2 1 3 t destination s red 1’ 1’’ 2’ 2’’ 3’ 3’’ 4’ 4’’ t We find a perfect matching (if possible) !!

How to find a properly edge-colored s -t path? Graph G’ blue 2 -edge-colored graph G 4 2 s 3 1 source t destination Therem: Jensen&Gutin[1998] s red 1’ 1’’ 2’ 2’’ 3’ 3’’ 4’ 4’’ t a pec s-t path in G G’ contains a perfect matching

Properly s-t path in edge-colored graphs (Szeider’s Algorithm – [2003]) v u s t start p q v’ v’’ u’ u’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 dest. s color 1 color 2 color 3 t p 1 p 2 p 3 q 2 q 3 pa pb pc qa qb q’ q’’ p’ (a) 3 -edge colored graph p’’ (b) non-colored graph

Properly s-t path in edge-colored graphs (Szeider’s Algorithm – [2003]) v u s t start p q v’ v’’ u’ u’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 dest. s color 1 color 2 color 3 t p 1 p 2 p 3 q 2 q 3 pa pb pc qa qc q’ q’’ p’ (a) 3 -edge colored graph p’’ (b) non-colored graph

Properly s-t path in edge-colored graphs (Szeider’s Algorithm – [2003]) v u s t start p q v’ v’’ u’ u’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 dest. s color 1 color 2 color 3 t p 1 p 2 p 3 q 2 q 3 pa pb pc qa qc q’ q’’ p’ (a) 3 -edge colored graph p’’ (b) non-colored graph

Properly s-t path in edge-colored graphs (Szeider’s Algorithm – [2003]) v u s t start p q v’ v’’ u’ u’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 dest. s color 1 color 2 color 3 t p 1 p 2 p 3 q 2 q 3 pa pb pc qa qb q’ q’’ p’ (a) 3 -edge colored graph p’’ (b) non-colored graph

Our results: How to find a prop. edge-colored s-t trail? Lemma: Consider a c-edge-colored graph G, and an arbitrary pec trail T between « s » and « t » . Further, suppose that at least one node in T is visited 3 times or more. Then, there exists another pec trail T’ where no nodes are visited more than 2 times a s x Cycles or closed trails passing by x b y t Almost cycles or closed trails passing by y

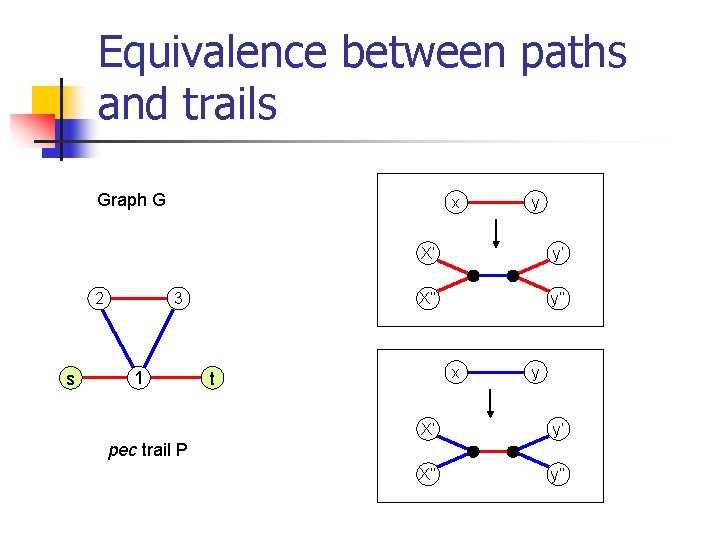
Equivalence between paths and trails Graph G 3 2 s x 1 y X’ y’ X’’ y’’ x t y X’ y’ X’’ y’’ pec trail P

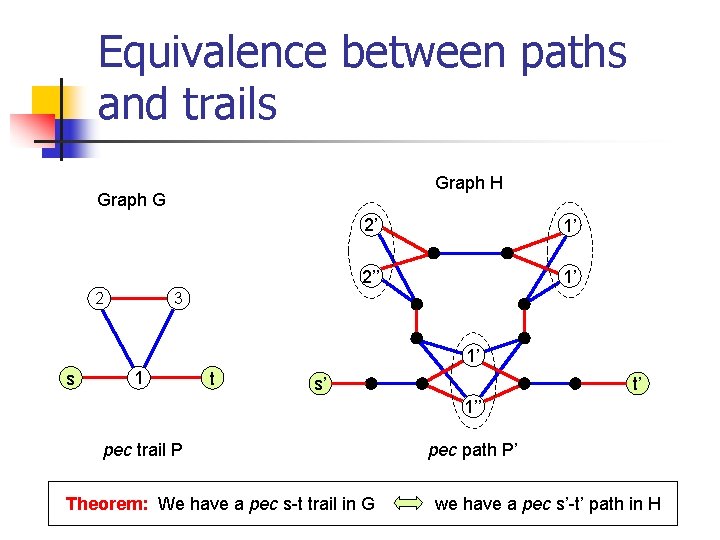
Equivalence between paths and trails Graph H Graph G 2’ 1’ 2’’ 1’ 3 2 1’ s 1 t s’ t’ 1’’ pec trail P pec path P’ Theorem: We have a pec s-t trail in G we have a pec s’-t’ path in H

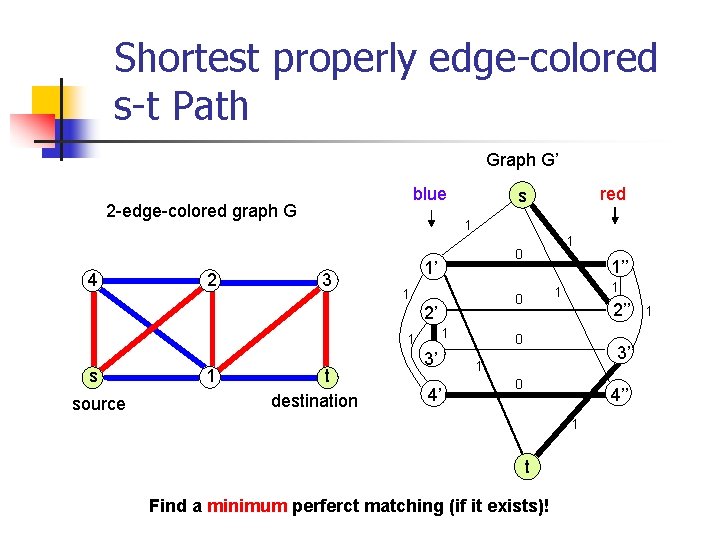
Shortest properly edge-colored s-t Path Graph G’ blue 2 -edge-colored graph G 4 2 1 3 1’ 1 source 1 t destination 1’’ 3’ 4’ 1 1 0 1 1 1 0 2’ s red s 2’’ 0 3’’ 1 0 4’’ 1 t Find a minimum perferct matching (if it exists)! 1

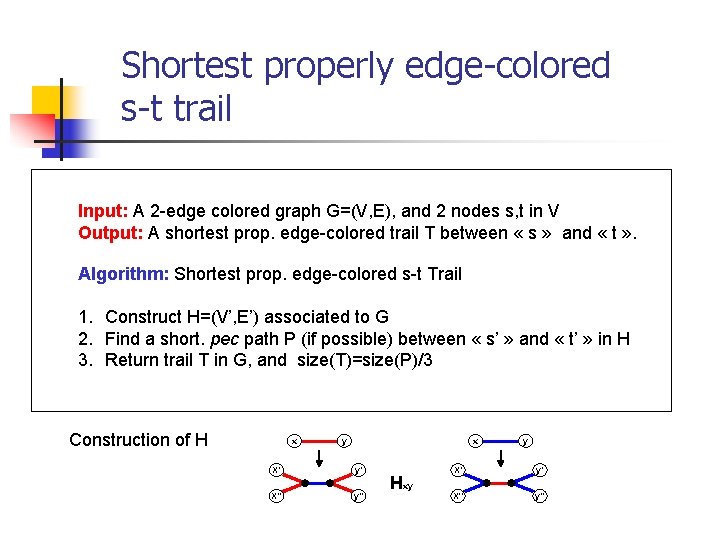
Shortest properly edge-colored s-t trail Input: A 2 -edge colored graph G=(V, E), and 2 nodes s, t in V Output: A shortest prop. edge-colored trail T between « s » and « t » . Algorithm: Shortest prop. edge-colored s-t Trail 1. Construct H=(V’, E’) associated to G 2. Find a short. pec path P (if possible) between « s’ » and « t’ » in H 3. Return trail T in G, and size(T)=size(P)/3 Construction of H x y x X’ y’ X’’ y’’ Hxy y X’ y’ X’’ y’’

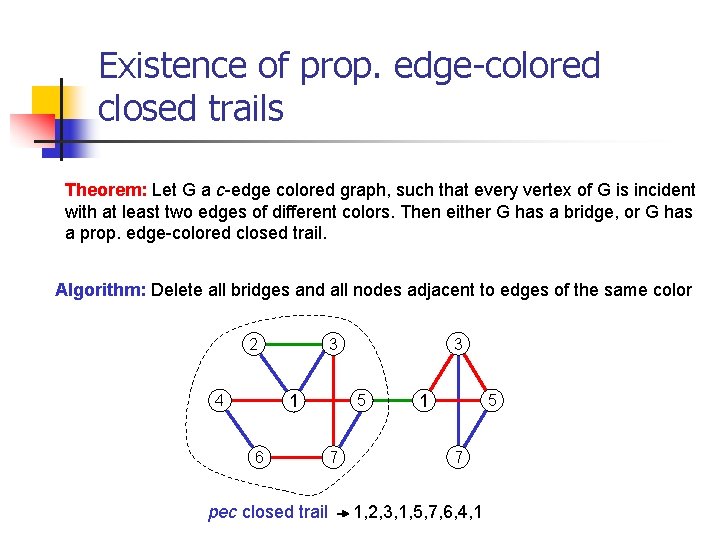
Existence of prop. edge-colored closed trails Theorem: Let G a c-edge colored graph, such that every vertex of G is incident with at least two edges of different colors. Then either G has a bridge, or G has a prop. edge-colored closed trail. Algorithm: Delete all bridges and all nodes adjacent to edges of the same color 1 4 6 3 3 2 5 7 1 5 7 pec closed trail 1, 2, 3, 1, 5, 7, 6, 4, 1

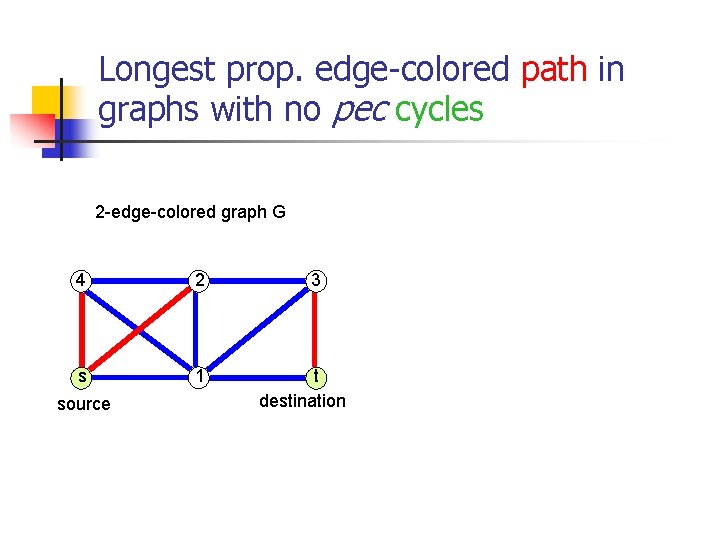
Longest prop. edge-colored path in graphs with no pec cycles 2 -edge-colored graph G 4 2 s 1 source 3 t destination

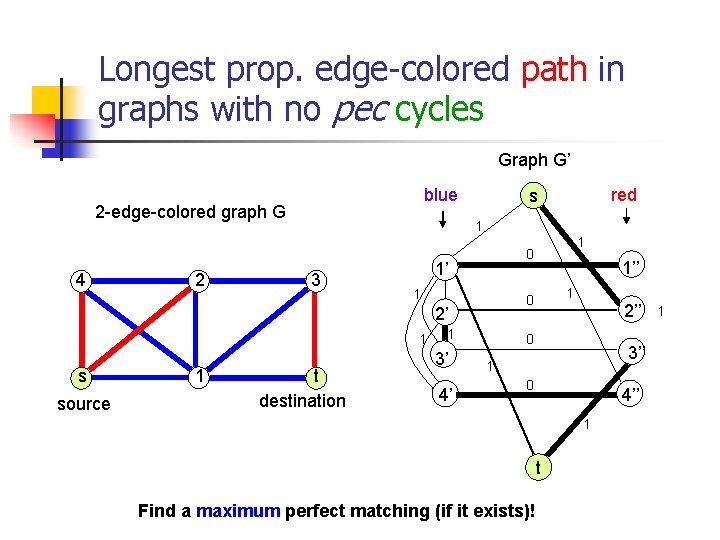
Longest prop. edge-colored path in graphs with no pec cycles Graph G’ blue 2 -edge-colored graph G 4 2 1 3 1’ 1 1 source 1 t destination 4’ 1’’ 1 0 1 3’ 1 0 2’ s red s 2’’ 0 3’’ 1 0 4’’ 1 t Find a maximum perfect matching (if it exists)! 1

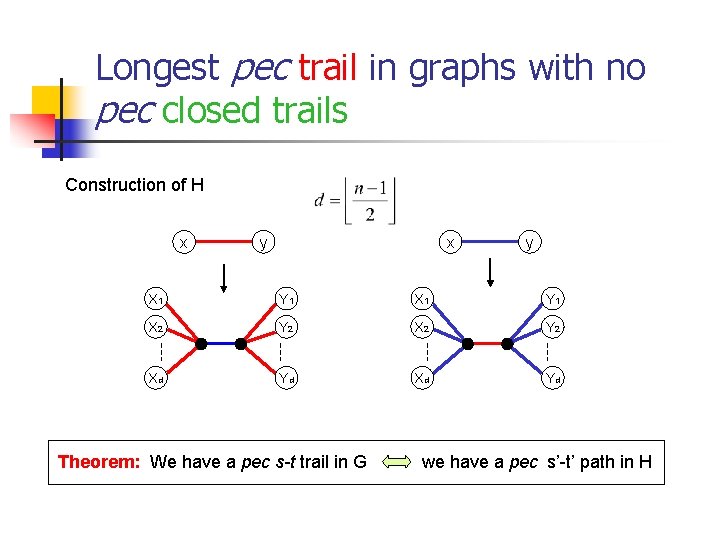
Longest pec trail in graphs with no pec closed trails s x y Cycles or closed trails passing by x (not possible !!) t Almost cycles or closed trails passing by y We can visit node « y » several times !! FACT: Node « y » can be visited at most times!

Longest pec trail in graphs with no pec closed trails s x y Cycles or closed trails passing by x (not possible !!) t Almost cycles or closed trails passing by y We can visit node « y » several times !! FACT: Node « y » can be visited at most times!

Longest pec trail in graphs with no pec closed trails Construction of H x y X 1 Y 1 X 2 Y 2 Xd Yd Theorem: We have a pec s-t trail in G we have a pec s’-t’ path in H

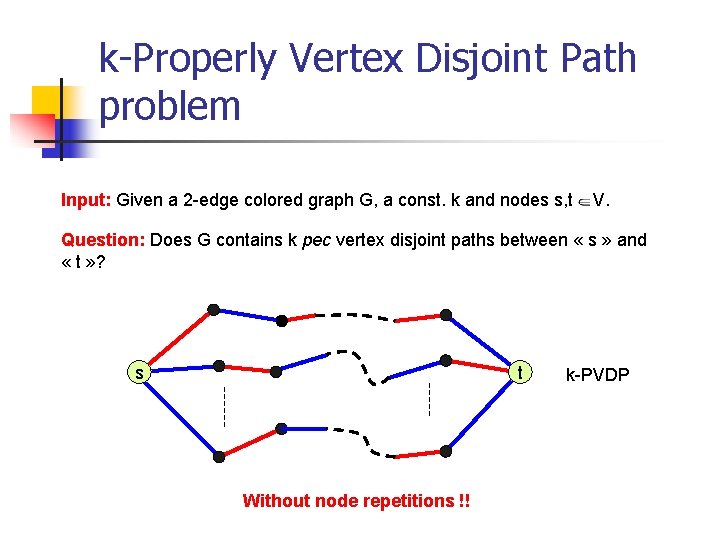
k-Properly Vertex Disjoint Path problem Input: Given a 2 -edge colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec vertex disjoint paths between « s » and « t » ? s t Without node repetitions !! k-PVDP

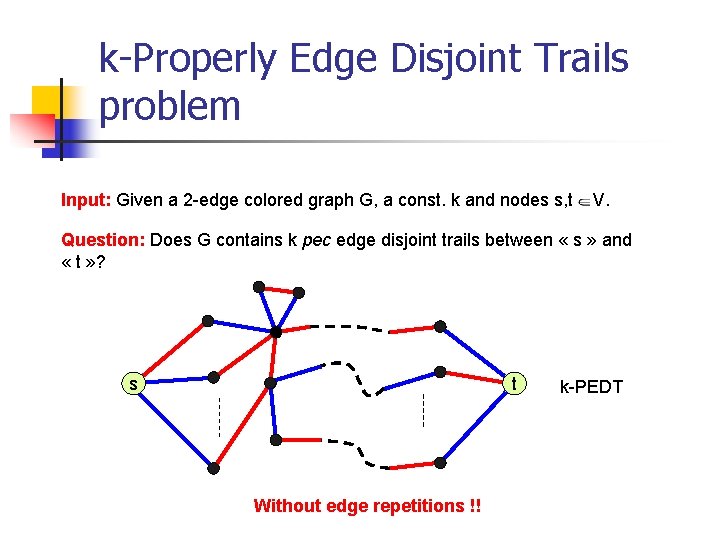
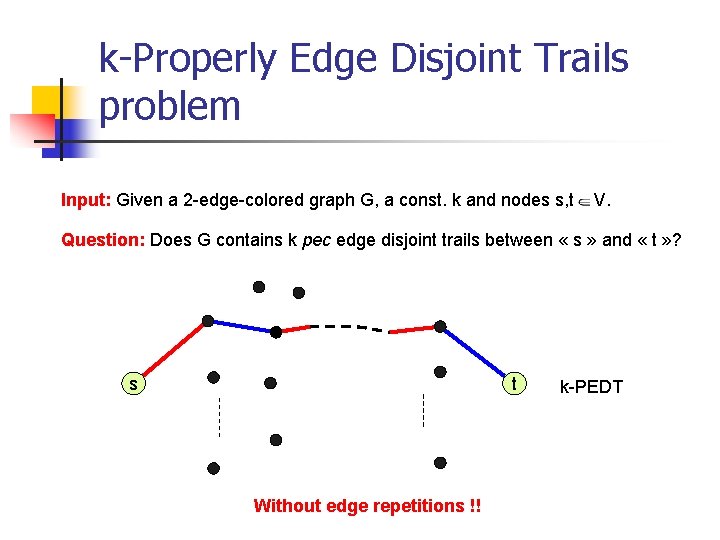
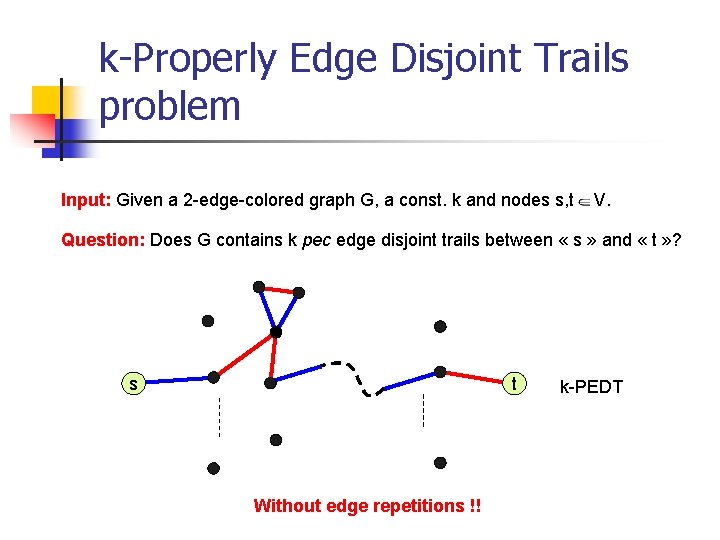
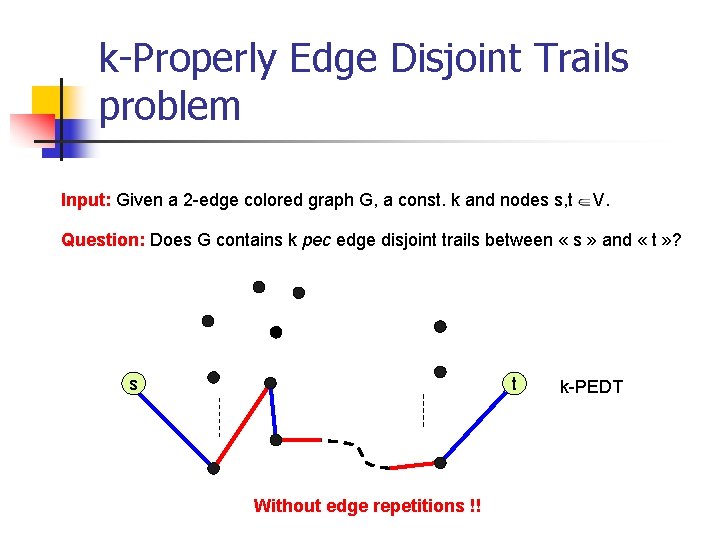
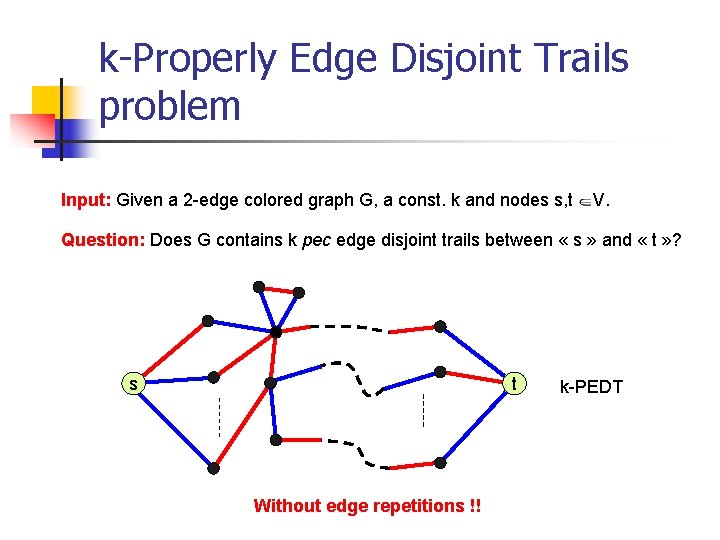
k-Properly Edge Disjoint Trails problem Input: Given a 2 -edge colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec edge disjoint trails between « s » and « t » ? s t Without edge repetitions !! k-PEDT

k-Properly Edge Disjoint Trails problem Input: Given a 2 -edge-colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec edge disjoint trails between « s » and « t » ? s t Without edge repetitions !! k-PEDT

k-Properly Edge Disjoint Trails problem Input: Given a 2 -edge-colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec edge disjoint trails between « s » and « t » ? s t Without edge repetitions !! k-PEDT

k-Properly Edge Disjoint Trails problem Input: Given a 2 -edge colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec edge disjoint trails between « s » and « t » ? s t Without edge repetitions !! k-PEDT

k-Properly Edge Disjoint Trails problem Input: Given a 2 -edge colored graph G, a const. k and nodes s, t V. Question: Does G contains k pec edge disjoint trails between « s » and « t » ? s t Without edge repetitions !! k-PEDT

NP-Completeness Input: A digraph D=(V, A) and a pair of nodes u, v V Directed cycle problem - DC u v Output: Does exist a vertex disjoint circuit passing by « u » and « v » ? Directed Closed-Trail problem - DCT Output: Does exist an arc disjoint Circuit passing by « u » and « v » ? Fortune, Hopcroft, Wylie [1980] Theorem: DC problem is NP-Complete

NP-Completeness Theorem: Both 2 -PVDP and 2 -PEDT problems are NP Complete on arbitrary 2 -edge-colored graphs. Proof : (sketch) 0. Both 2 -PVDP and 2 -PEDT are in NP 1. Reduction: DC problem 2 -PVDP 2. Lemma: DCT problem is NP-Complete. 3. Reduction: DCT problem 2 -PEDT

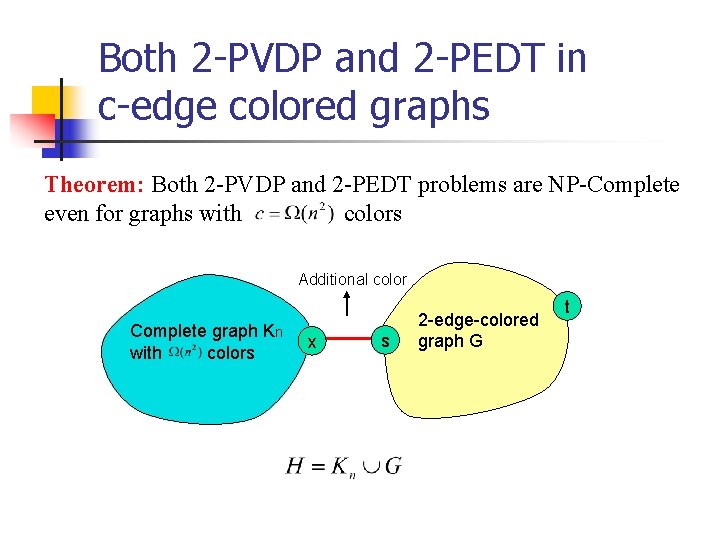
Both 2 -PVDP and 2 -PEDT in c-edge colored graphs Theorem: Both 2 -PVDP and 2 -PEDT problems are NP-Complete even for graphs with colors Additional color Complete graph Kn with colors x s 2 -edge-colored graph G t

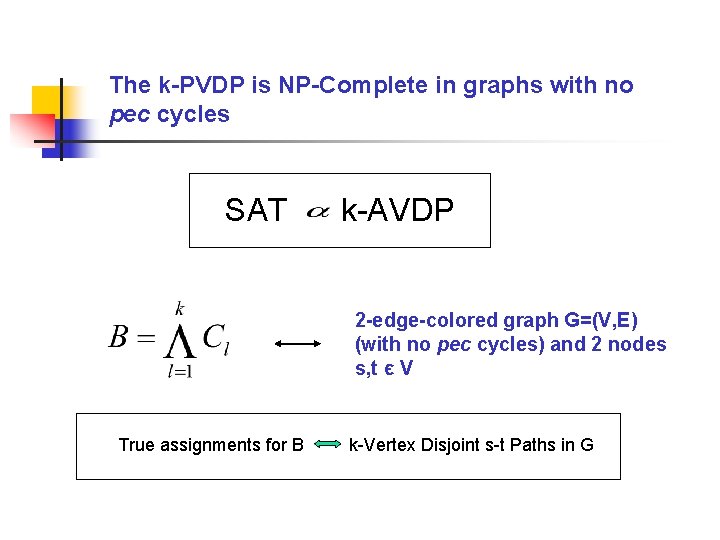
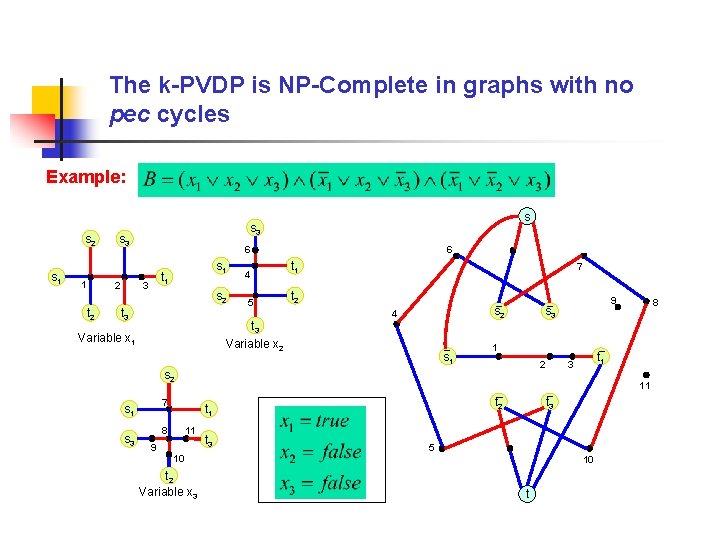
The k-PVDP is NP-Complete in graphs with no pec cycles SAT k-AVDP 2 -edge-colored graph G=(V, E) (with no pec cycles) and 2 nodes s, t є V True assignments for B k-Vertex Disjoint s-t Paths in G

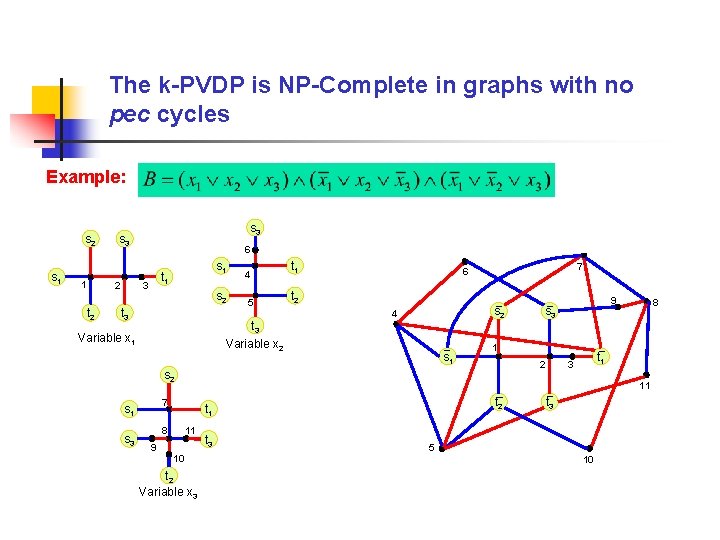
The k-PVDP is NP-Complete in graphs with no pec cycles Example: s 2 s 1 1 2 t 2 s 3 6 s 1 t 1 3 s 2 t 3 4 5 t 3 Variable x 2 Variable x 1 t 1 7 6 t 2 s 2 4 s 1 1 2 s 3 t 2 t 1 8 8 t 1 3 11 7 s 1 9 s 3 11 9 10 t 2 Variable x 3 t 3 5 10

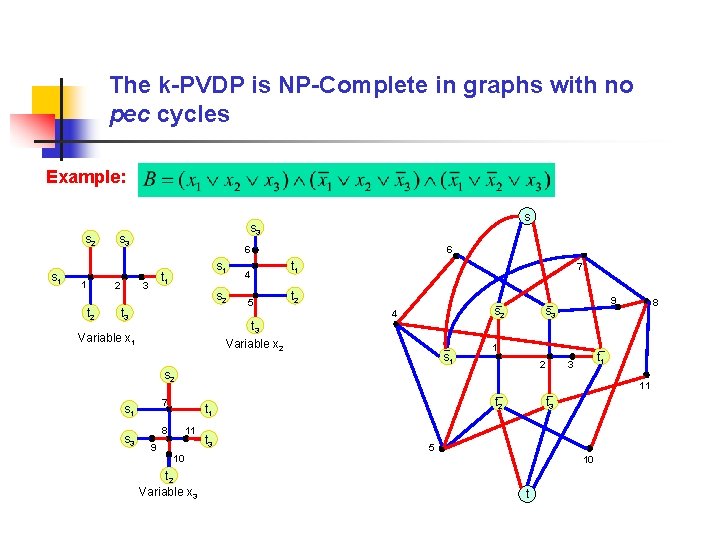
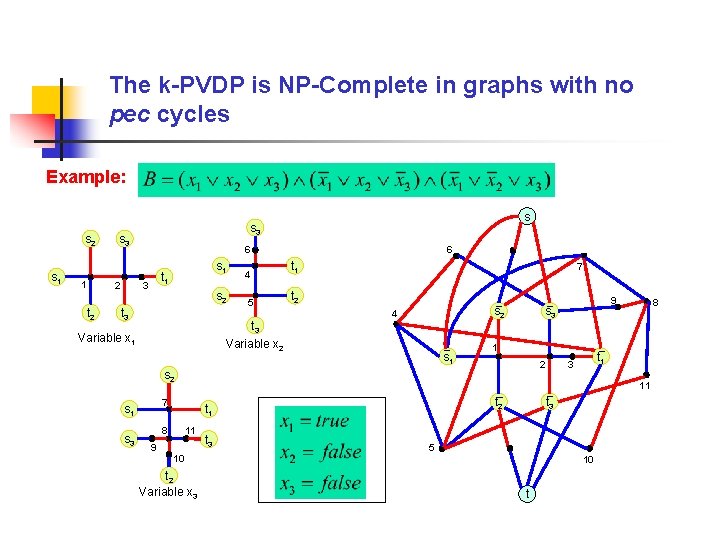
The k-PVDP is NP-Complete in graphs with no pec cycles Example: s 2 s 1 1 s 3 2 t 2 s s 3 6 s 1 t 1 3 s 2 t 3 4 5 t 3 Variable x 2 Variable x 1 6 t 1 7 t 2 s 2 4 s 1 1 2 s 3 t 2 t 1 8 8 t 1 3 11 7 s 1 9 s 3 11 9 t 3 5 10 t 2 Variable x 3 10 t

The k-PVDP is NP-Complete in graphs with no pec cycles Example: s 2 s 1 1 s 3 2 t 2 s s 3 6 s 1 t 1 3 s 2 t 3 4 5 t 3 Variable x 2 Variable x 1 6 t 1 7 t 2 s 2 4 s 1 1 2 s 3 t 2 t 1 8 8 t 1 3 11 7 s 1 9 s 3 11 9 t 3 5 10 t 2 Variable x 3 10 t

The k-PVDP is NP-Complete in graphs with no pec cycles Example: s 2 s 1 1 s 3 2 t 2 s s 3 6 s 1 t 1 3 s 2 t 3 4 5 t 3 Variable x 2 Variable x 1 6 t 1 7 t 2 s 2 4 s 1 1 2 s 3 t 2 t 1 8 8 t 1 3 11 7 s 1 9 s 3 11 9 t 3 5 10 t 2 Variable x 3 10 t

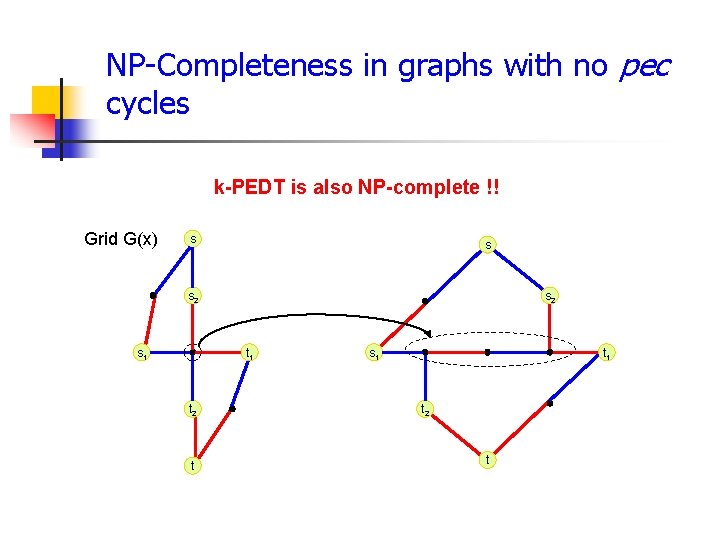
NP-Completeness in graphs with no pec cycles k-PEDT is also NP-complete !! Grid G(x) s s s 2 s 1 s 2 t 1 t 2 t s 1 t 2 t

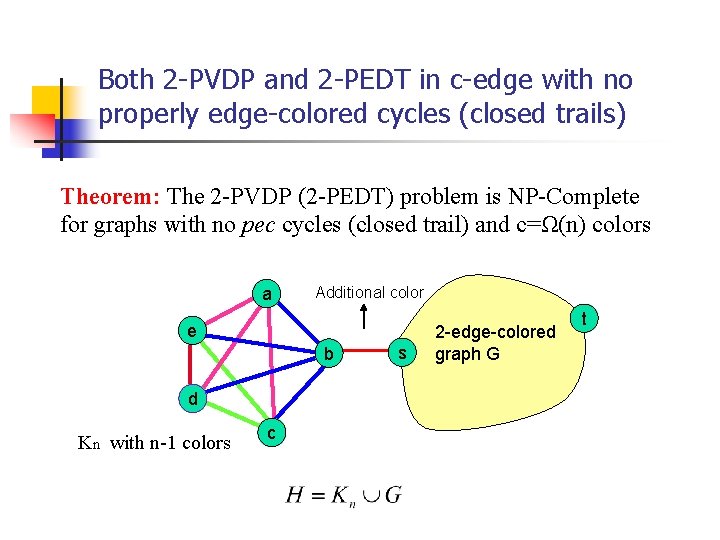
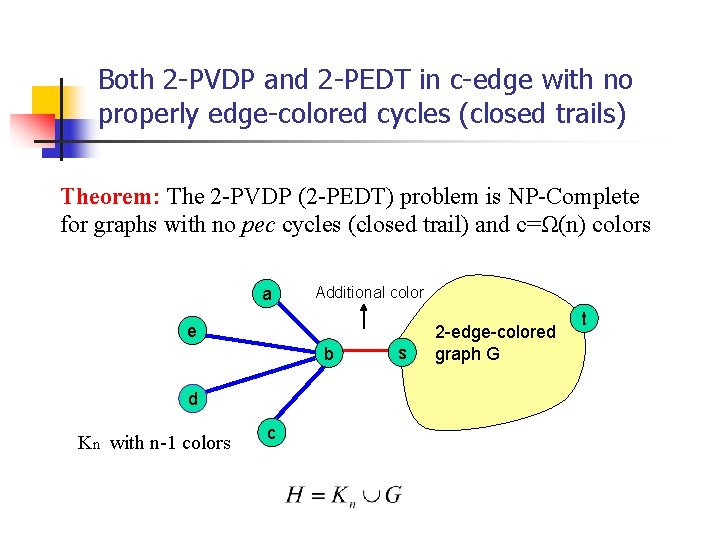
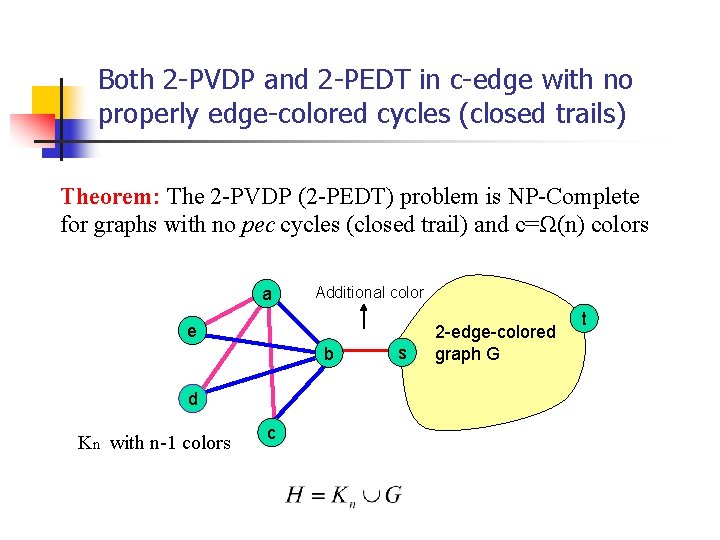
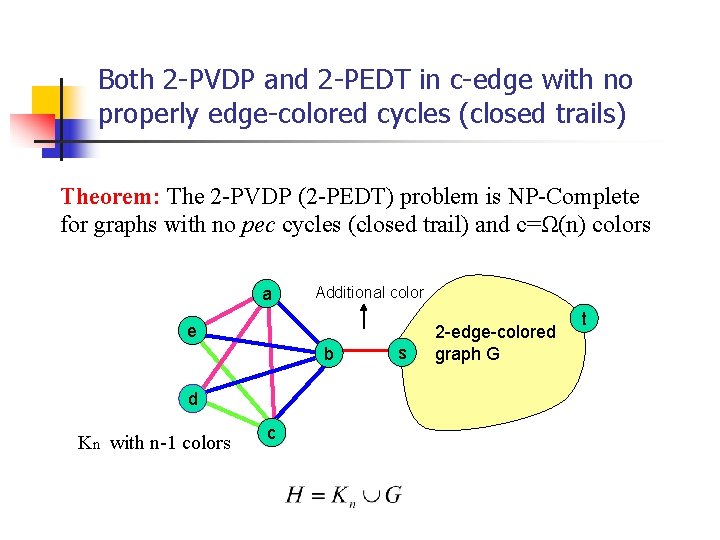
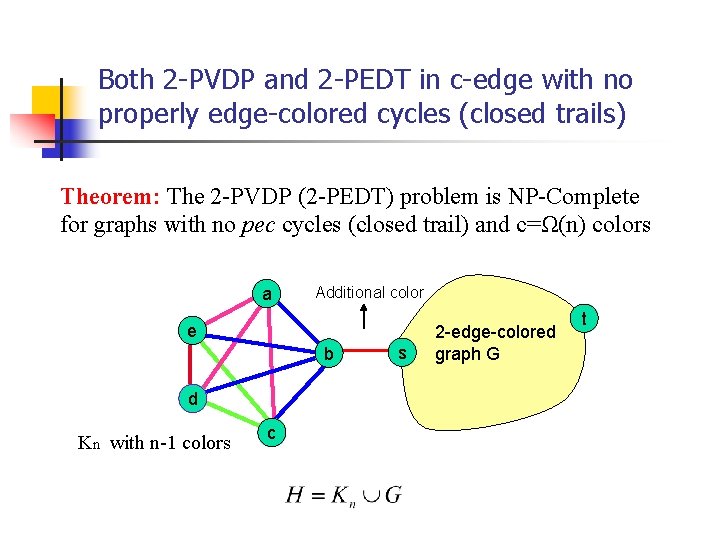
Both 2 -PVDP and 2 -PEDT in c-edge with no properly edge-colored cycles (closed trails) Theorem: The 2 -PVDP (2 -PEDT) problem is NP-Complete for graphs with no pec cycles (closed trail) and c=Ω(n) colors a Additional color e b d Kn with n-1 colors c s 2 -edge-colored graph G t

Both 2 -PVDP and 2 -PEDT in c-edge with no properly edge-colored cycles (closed trails) Theorem: The 2 -PVDP (2 -PEDT) problem is NP-Complete for graphs with no pec cycles (closed trail) and c=Ω(n) colors a Additional color e b d Kn with n-1 colors c s 2 -edge-colored graph G t

Both 2 -PVDP and 2 -PEDT in c-edge with no properly edge-colored cycles (closed trails) Theorem: The 2 -PVDP (2 -PEDT) problem is NP-Complete for graphs with no pec cycles (closed trail) and c=Ω(n) colors a Additional color e b d Kn with n-1 colors c s 2 -edge-colored graph G t

Both 2 -PVDP and 2 -PEDT in c-edge with no properly edge-colored cycles (closed trails) Theorem: The 2 -PVDP (2 -PEDT) problem is NP-Complete for graphs with no pec cycles (closed trail) and c=Ω(n) colors a Additional color e b d Kn with n-1 colors c s 2 -edge-colored graph G t

Both 2 -PVDP and 2 -PEDT in c-edge with no properly edge-colored cycles (closed trails) Theorem: The 2 -PVDP (2 -PEDT) problem is NP-Complete for graphs with no pec cycles (closed trail) and c=Ω(n) colors a Additional color e b d Kn with n-1 colors c s 2 -edge-colored graph G t

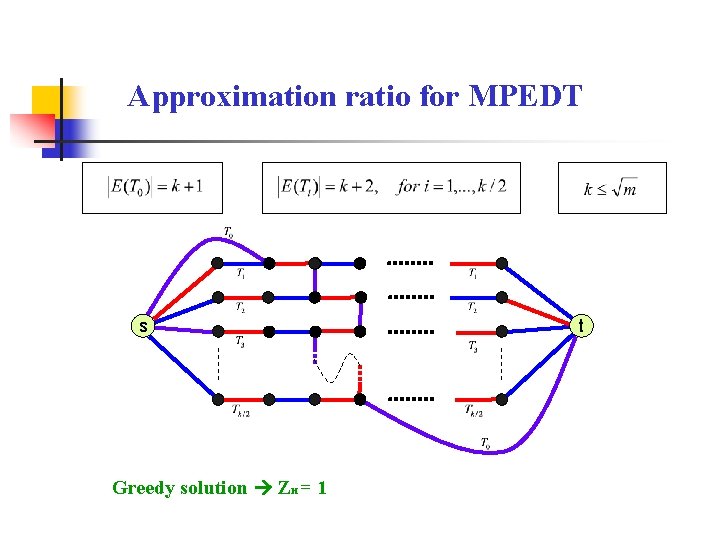
Approximation Algorithm for the MPEDT Greedy-ED Procedure 1. S Ø 2. Repeat Find an pec shortest trail T between « s » and « t » ; S S E(T); E E - E(T); Until (no pec s-t trails are found) Theorem: The Greedy-ED has performance ratio equal to for the MPEDT problem

Approximation Algorithm for the MPVDP Greedy-VD Procedure 1. S Ø 2. Repeat Find a pec shortest path P between « s » and « t » ; S S E(P); V V - V(P); Until (no pec s-t paths are found) Theorem: The Greedy-VD has performance ratio equal to for the MPVDP problem

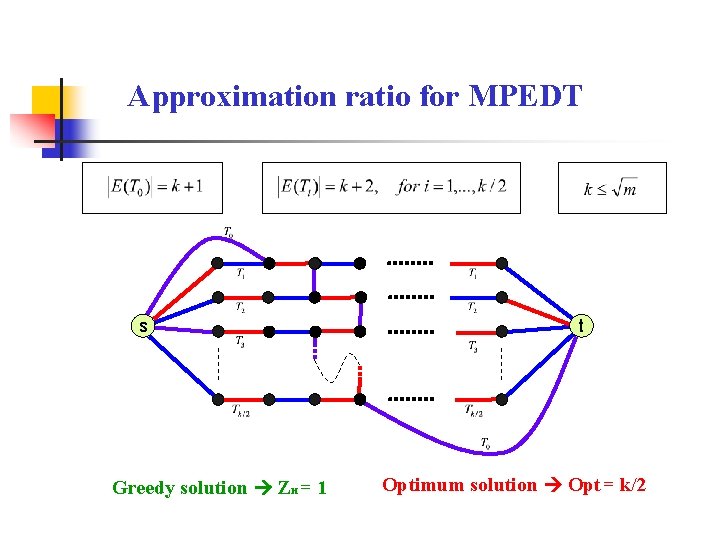
Approximation ratio for MPEDT s Greedy solution ZH = 1 t

Approximation ratio for MPEDT s Greedy solution ZH = 1 t Optimum solution Opt = k/2

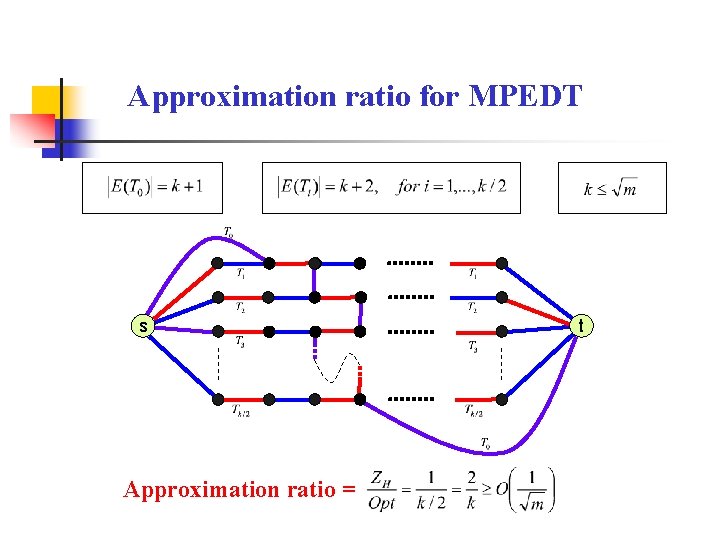
Approximation ratio for MPEDT s Approximation ratio = t

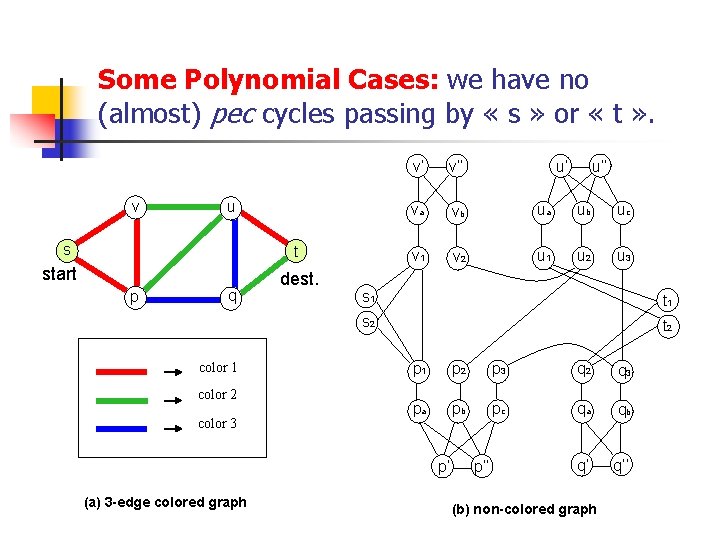
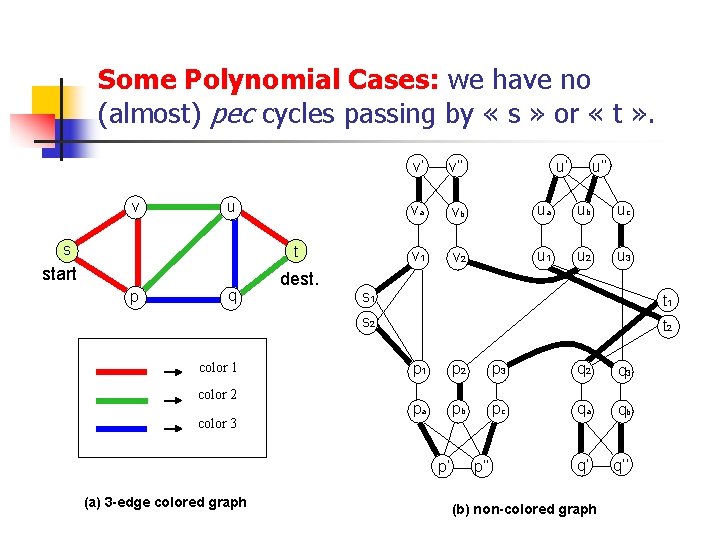
Some Polynomial Cases: we have no (almost) pec cycles passing by « s » or « t » . v u s t start p q color 1 color 2 color 3 dest. v’ v’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 u’’ s 1 t 1 s 2 t 2 p 1 p 2 p 3 q 2 q 3 pa pb pc qa qb q’ q’’ p’ (a) 3 -edge colored graph u’ p’’ (b) non-colored graph

Some Polynomial Cases: we have no (almost) pec cycles passing by « s » or « t » . v u s t start p q color 1 color 2 color 3 dest. v’ v’’ va vb ua ub uc v 1 v 2 u 1 u 2 u 3 u’’ s 1 t 1 s 2 t 2 p 1 p 2 p 3 q 2 q 3 pa pb pc qa qb q’ q’’ p’ (a) 3 -edge colored graph u’ p’’ (b) non-colored graph

Open Problems and Future Diretions Input: Given a 2 -edge-colored graph with no pec cycles, vertices s, t V(G) and a fixed k 2. Question: Does G contains k pec vertex disjoint paths between « s » and « t » ? Input: Given a c-edge-colored complete graph , and vertices s, t of Open question: Maximize the number of edge-disjoint pec s-t paths in is in P? Future work: What about the performance ratio of both MPVDP and MPEDT problems in graphs with no pec cycles (closed trails)?

Thanks for your attention!!