Latihan Soal Solve the following linear program using

Latihan Soal

• Solve the following linear program using the graphical solution procedure! Max Z= 5 X 1+5 X 2 Subject to: X 1≤ 100 X 2≤ 80 2 X 1+ 4 X 2 ≤ 400 X 1 , X 2 ≥ 0 • • Diketahui permasalahan PL sebagai berikut: Maks. Z = 5 x 1 + 10 x 2 kendala: 5 x 1 + 10 x 2 60 4 x 1 + 4 x 2 40 5 x 1 40 dengan x 1; x 2 0 Bagaimana kondisi solusinya? Selesaikan dengan metode simplex

• Perusahaan ABC memproduksi 2 jenis produk, yaitu cangkir dan mangkok. Harga jual untuk cangkir dan mangkok berturut -turut adalah $2 dan $3. Untuk memproduksi sebuah cangkir dibutuhkan 1 jam dengan pekerja sejumlah 5 orang. Sedangkan untuk memproduksi mangkok dibutuhkan 2 jam dengan jumlah pekerja 3 orang. Jam kerja yang tersedia per hari adalah 6 jam, sedangkan jumlah tenaga kerja yang dimiliki perusahaan ABC sejumlah 15 orang. Berapakah jumlah cangkir dan mangkok yang harus diproduksi agar pendapatan maksimal? Berdasarkan infomasi tersebut: • Buatlah formulasi modelnya! • Selesaikan pemodelan tersebut menggunakan metode simpleks/grafis/revised simpleks! Berapakah cangkir dan mangkok yang harus diproduksi dan berapa pendapatan maksimalnya? • Buatlah model dual-nya! Dan buktikan bahwa nilai Z untuk model primal dan dual sama!

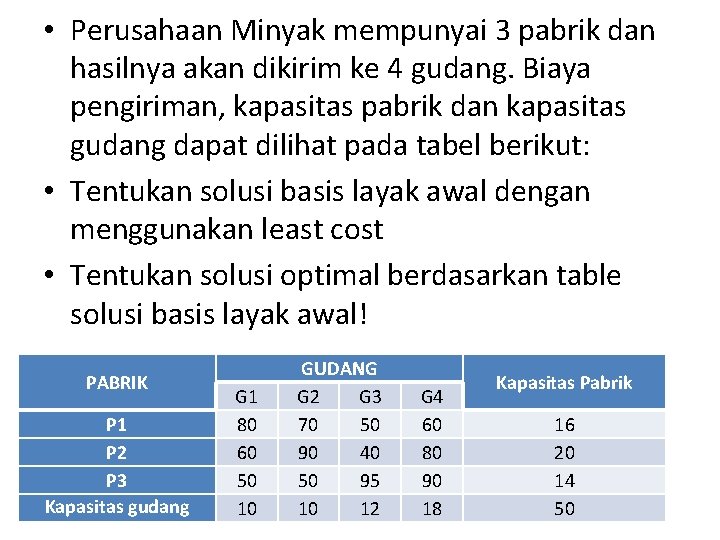
• Perusahaan Minyak mempunyai 3 pabrik dan hasilnya akan dikirim ke 4 gudang. Biaya pengiriman, kapasitas pabrik dan kapasitas gudang dapat dilihat pada tabel berikut: • Tentukan solusi basis layak awal dengan menggunakan least cost • Tentukan solusi optimal berdasarkan table solusi basis layak awal! PABRIK P 1 P 2 P 3 Kapasitas gudang G 1 80 60 50 10 GUDANG G 2 G 3 70 50 90 40 50 95 10 12 G 4 60 80 90 18 Kapasitas Pabrik 16 20 14 50

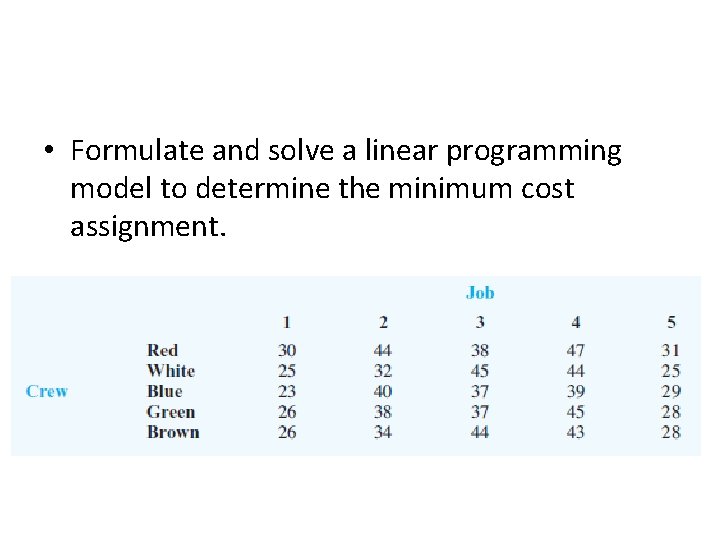
• Formulate and solve a linear programming model to determine the minimum cost assignment.