Last week inplace sorting Bubble Sort On 2

Last week: in-place sorting • Bubble Sort – O(n 2) comparisons – O(n) best case comparisons, O(n 2) exchanges • Selection Sort - O(n 2) comparisons – O(n 2) best case comparisons – O(n) exchanges (always) • Insertion Sort – O(n 2) comparisons – O(n) best case comparisons – Fewer exchanges than bubble sort – Best in practice for small lists (<30)

This week • Mergesort – O(n log n) always – O(n) storage • Quick sort – O(n log n) average, O(n^2) worst – Good in practice (>30), O(log n) storage

Merge. Sort • A divide-and-conquer technique • Each unsorted collection is split into 2 – Then again • Then again – Then again » ……. Until we have collections of size 1 » Now we merge sorted collections – Then again • Then again – Then again • Until we merge the two halves

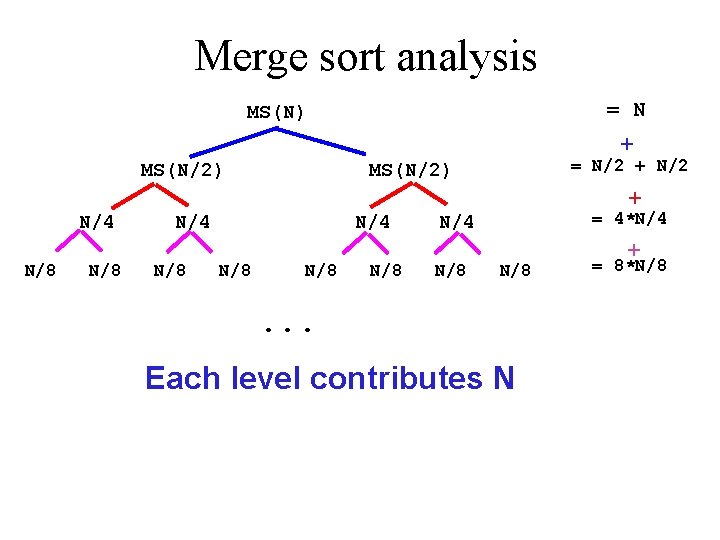
Merge sort analysis = N MS(N) + MS(N/2) = N/2 + N/2 MS(N/2) + N/4 N/8 N/8 = 4*N/4 N/8 . . . Each level contributes N + = 8*N/8

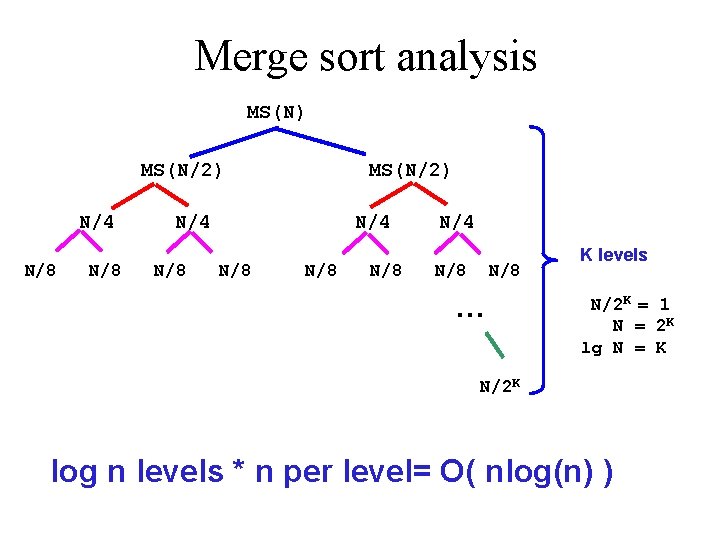
Merge sort analysis MS(N) MS(N/2) N/4 N/8 N/8 N/4 N/8 … K levels N/2 K = 1 N = 2 K lg N = K N/2 K log n levels * n per level= O( nlog(n) )

Merge. Sort(array a, indexes low, high) 1. If (low < high) 2. middle (low + high) /2 3. Merge. Sort(a, low, middle) // split 1 4. Merge. Sort(a, middle+1, high) // split 2 5. Merge(a, low, middle, high) // merge 1+2

Merge(arrays a, index low, mid, high) 1. b empty array, t mid+1, i low, tl low 2. while (tl<=mid AND t<=high) 3. if (a[tl]<=a[t]) 4. b[i] a[tl] 5. i i+1, tl tl+1 6. else 7. b[i] a[t] 8. i i+1, t t+1 9. if tl<=mid copy a[tl…mid] into b[i…] 10. else if t<=high copy a[t…high] into b[i…] 11. copy b[low…high] onto a[low…high]

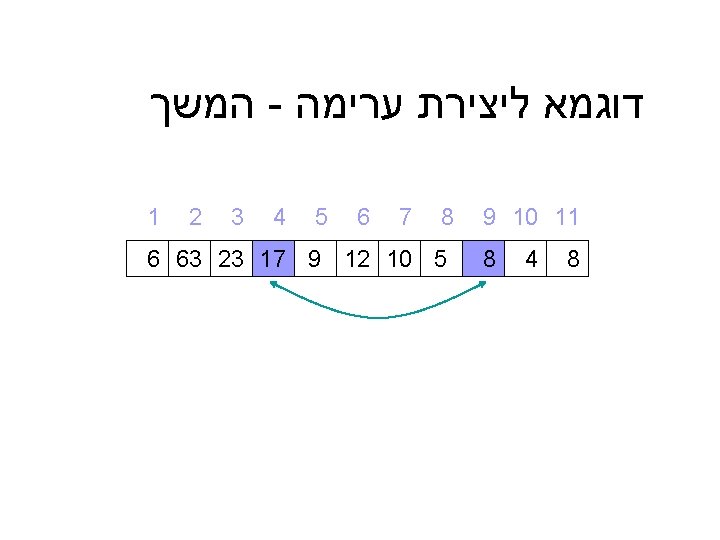
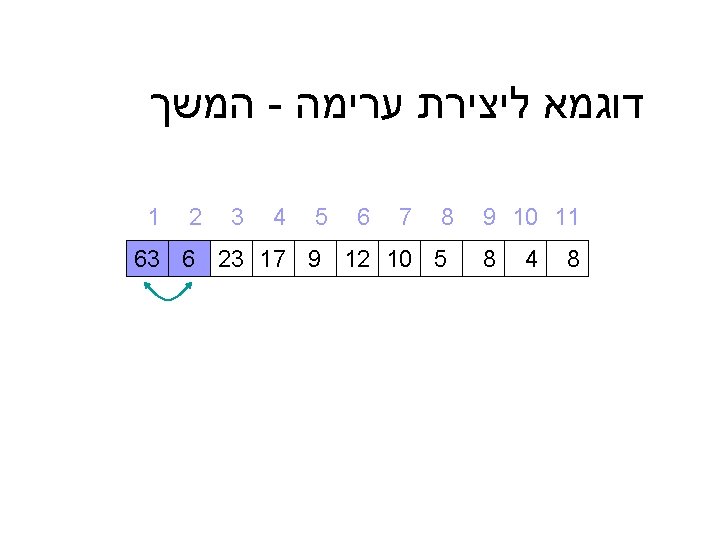
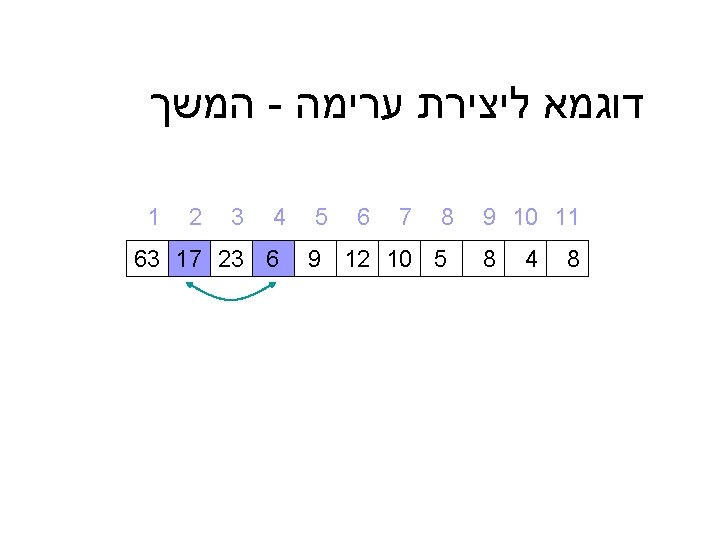
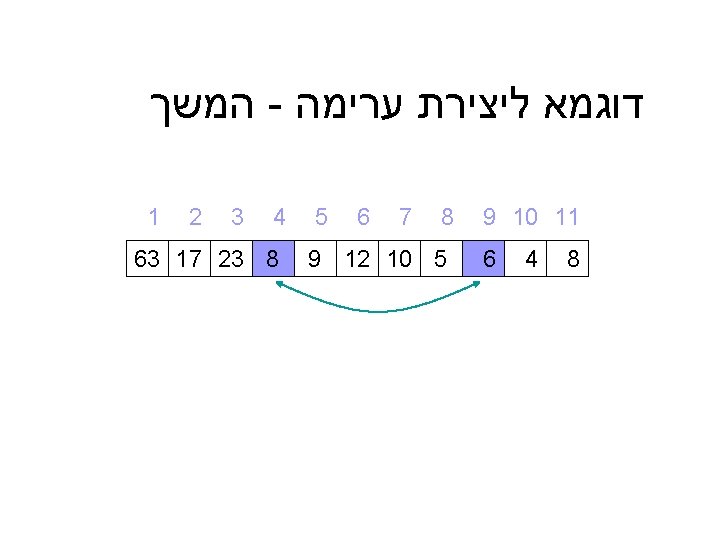
דוגמא Initial: 25 57 48 37 12 92 86 33 Split: 25 57 48 37 12 92 86 33 Merge: 25 57 37 48 12 92 33 86 Merge: 25 37 48 57 12 33 86 92 Merge: 12 25 33 37 48 57 86 92

The complexity of Merge. Sort • Every split, we half the collection • How many times can this be done? We are looking for x, where 2 x = n x = log 2 n • So there a total of log n splits

The complexity of Merge. Sort • • • Each merge is of what run-time? First merge step: n/2 merges of 2 n Second merge step: n/4 merges of 4 n Third merge step: n/8 merges of 8 n …. How many merge steps? Same as splits log n Total: n log n steps

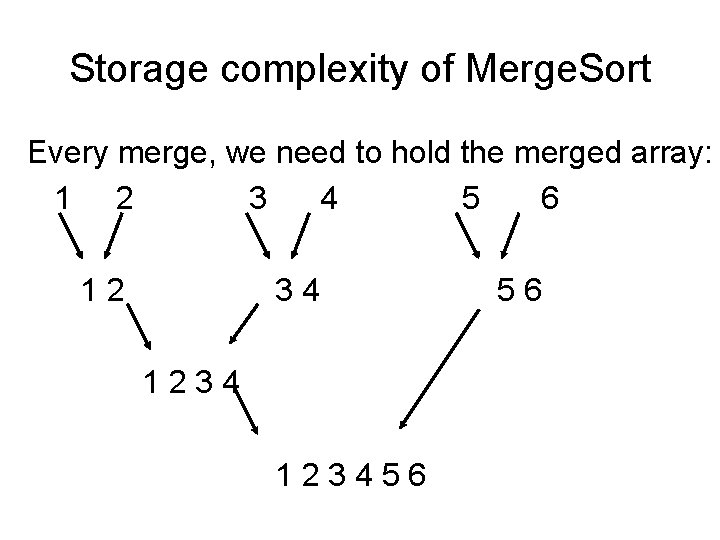
Storage complexity of Merge. Sort Every merge, we need to hold the merged array: 1 2 3 4 5 6 12 34 123456 56

Storage complexity of Merge. Sort • So we need temporary storage for merging – Which is the same size as the two collections together To merge the last two sub-arrays (each size n/2) We need n/2+n/2 = n temporary storage • Total: O(n) storage

Quick. Sort Key idea: • Select a item (called the pivot) • Put it into its proper FINAL position • Make sure: – All greater item are on one side (side 1) – All smaller item are on other side (side 2) • Repeat for side 1 • Repeat for side 2

Short example 25 57 48 37 12 92 86 33 • Let’s select 25 as our initial pivot. • We move items such that: – All left of 25 are smaller – All right of 25 are larger – As a result 25 is now in its final position 12 25 57 48 37 92 86 33

• Now, repeat (recursively) for left and right sides 12 25 57 48 37 92 86 33 – Sort 12 – Sort 57 48 37 92 86 33 • 12 needs no sorting • For the other side, we repeat the process – Select a pivot item (let’s take 57) – Move items around such that left items are

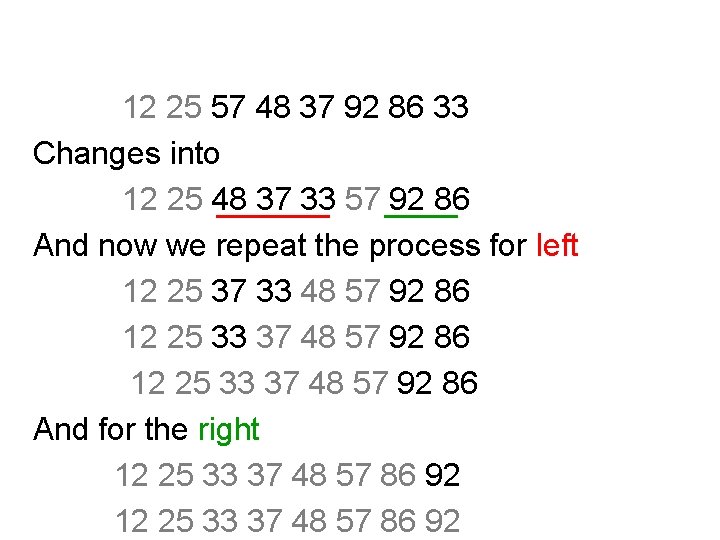
12 25 57 48 37 92 86 33 Changes into 12 25 48 37 33 57 92 86 And now we repeat the process for left 12 25 37 33 48 57 92 86 12 25 33 37 48 57 92 86 And for the right 12 25 33 37 48 57 86 92

Quick. Sort(array a; index low, hi) 1. 2. 3. 4. 5. 6. if (low >= hi) return ; // a[low. . hi] is sorted pivot find_pivot(a, low, hi) p_index=partition(a, low, high, pivot) Quick. Sort(a, low, p_index-1) Quick. Sort(a, p_index+1, hi)

Key questions How do we select an item (Find. Pivot())? • If we always select the largest item as the pivot – Then this process becomes Selection Sort – Which is O(n 2) • So this works only if we select items “in the middle” – Since then we will have log n divisions How do we move items around efficiently (Partition()? ) • This offsets the benefit of partitioning

Find. Pivot • • • To find a real median (middle item) takes O(n) In practice however, we want this to be O(1) So we approximate: – Take the first item (a[low]) as the pivot – Take the median of {a[low], a[hi], a[(low+hi)/2]} Find. Pivot(array a; index low, high) 1. return a[low]

Partition (in O(n)) Key idea: • Keep two indexes into the array – up points at lowest item >= pivot – down points at highest item <= pivot • We move up, down in the array • Whenever they point inconsistently, interchange At end: • up and down meet in location of pivot

partition(array a; index low, hi; pivot; index pivot_i) 1. down low, up hi 2. while(down<up) 3. while (a[down]<=pivot && down<hi) 4. down + 1 5. while (a[hi]>pivot) 6. up up – 1 7. if (down < up) 8. swap(a[down], a[up]) 9. a[pivot_i]=a[up] 10. a[up] = pivot 11. return up

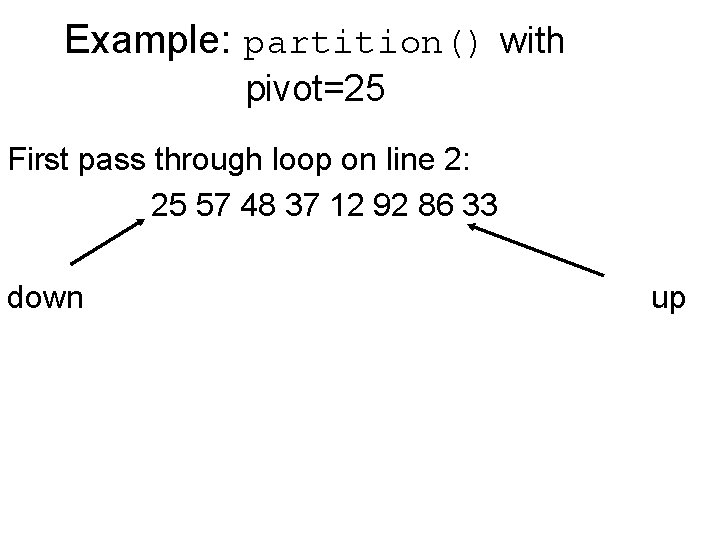
Example: partition() with pivot=25 First pass through loop on line 2: 25 57 48 37 12 92 86 33 down up

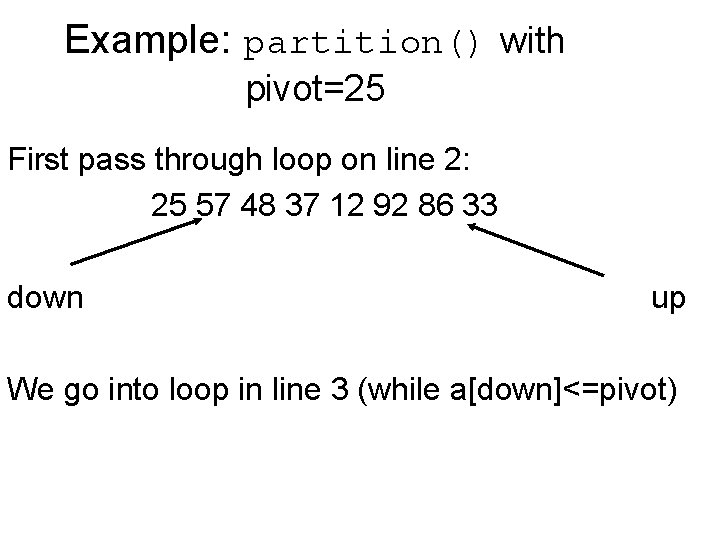
Example: partition() with pivot=25 First pass through loop on line 2: 25 57 48 37 12 92 86 33 down up We go into loop in line 3 (while a[down]<=pivot)

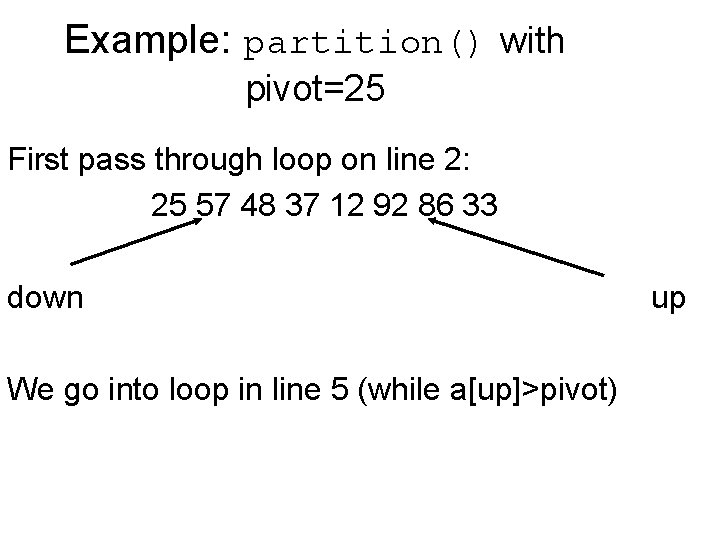
Example: partition() with pivot=25 First pass through loop on line 2: 25 57 48 37 12 92 86 33 down We go into loop in line 5 (while a[up]>pivot) up

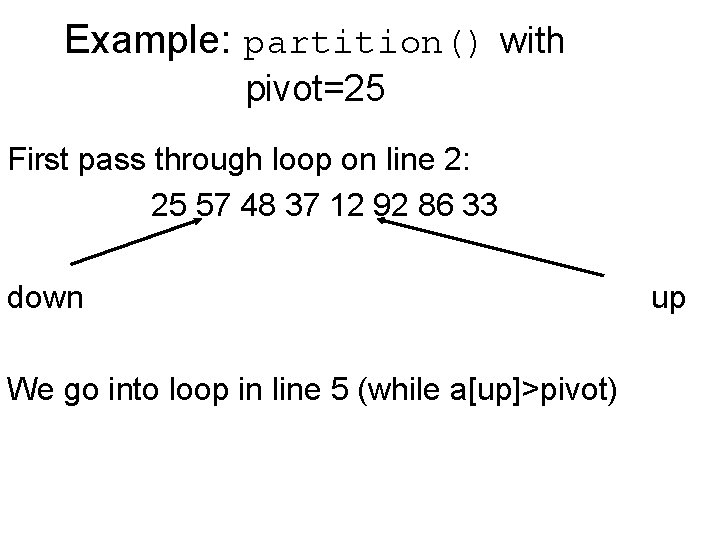
Example: partition() with pivot=25 First pass through loop on line 2: 25 57 48 37 12 92 86 33 down We go into loop in line 5 (while a[up]>pivot) up

Example: partition() with pivot=25 First pass through loop on line 2: 25 57 48 37 12 92 86 33 down Now we found an inconsistency! up

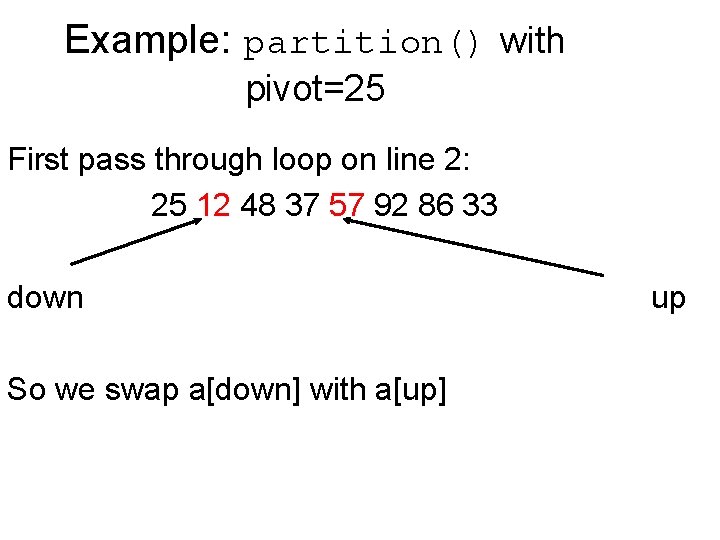
Example: partition() with pivot=25 First pass through loop on line 2: 25 12 48 37 57 92 86 33 down So we swap a[down] with a[up] up

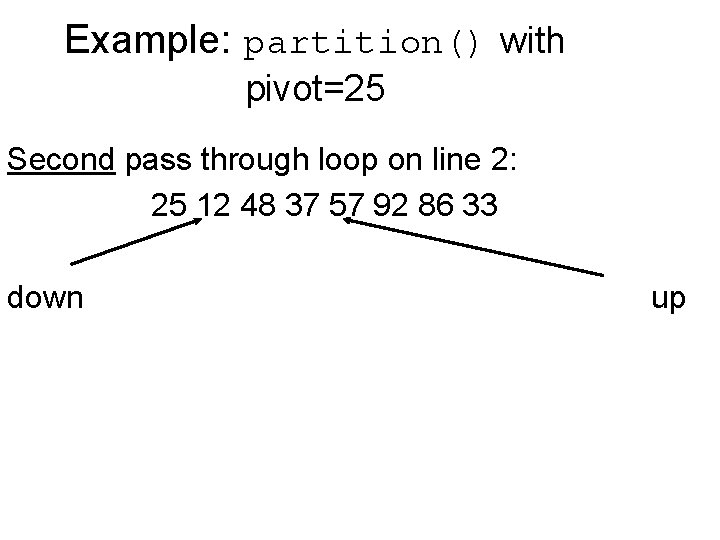
Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down up

Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down up Move down again (increasing) – loop on line 3

Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down up Now we begin to move up again – loop on line 5

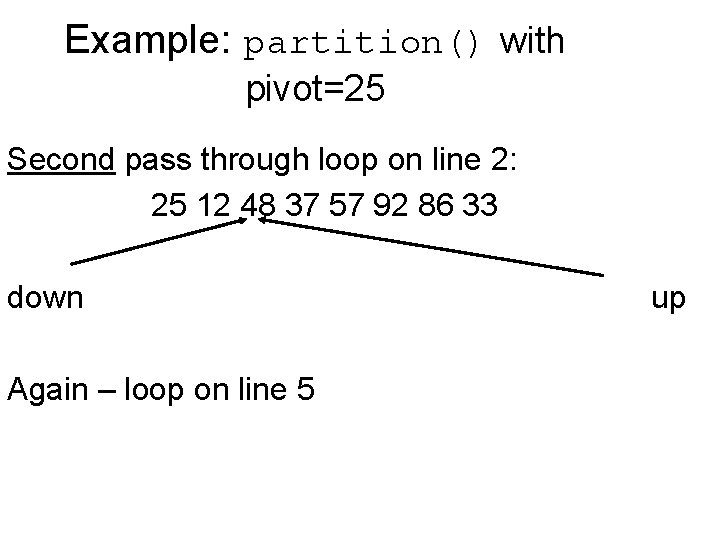
Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down Again – loop on line 5 up

Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down < up? No. So we don’t swap. up

Example: partition() with pivot=25 Second pass through loop on line 2: 25 12 48 37 57 92 86 33 down Instead, we are done. Just put pivot in place. up

Example: partition() with pivot=25 Second pass through loop on line 2: 12 25 48 37 57 92 86 33 down up Instead, we are done. Just put pivot in place. (swap it with a[up] – for us a[low] was the pivot)

Example: partition() with pivot=25 Second pass through loop on line 2: 12 25 48 37 57 92 86 33 down Now we return 2 as the new pivot index up

Notes • We need the initial pivot_index in partition() • For instance, change Find. Pivot(): – return pivot (a[low]), as well as initial pivot_index (low) – Then use pivot_index in the final swap • Quick. Sort: Average O(n log n), Worst case O(n 2) – works very well in practice (collections >30) – Average O(n log n), Worst case O(n 2) – Space requirements O(log n) – for recursion

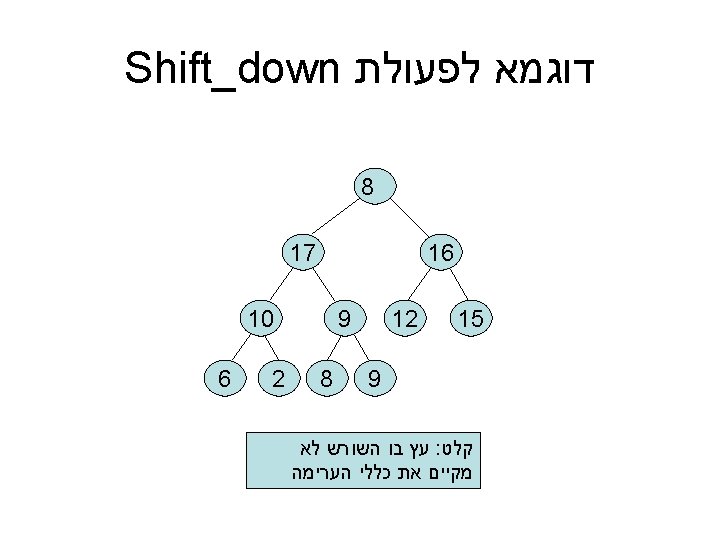
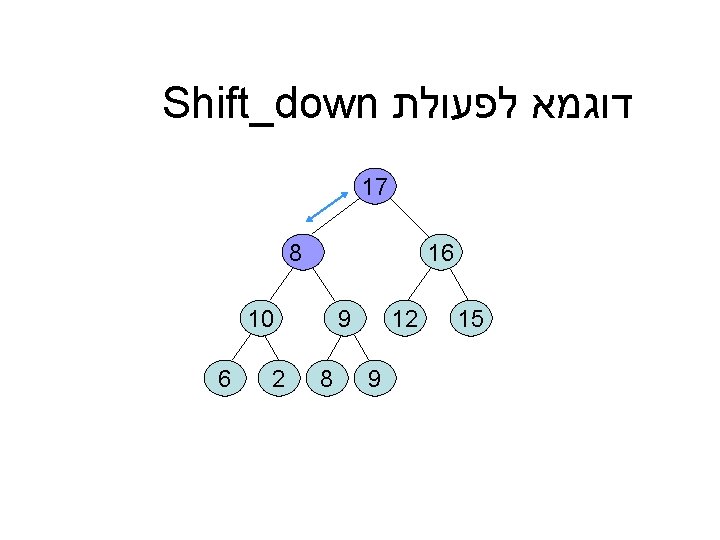
דוגמא לפעולת Shift_down 17 16 15 8 12 9 9 10 8 2 6

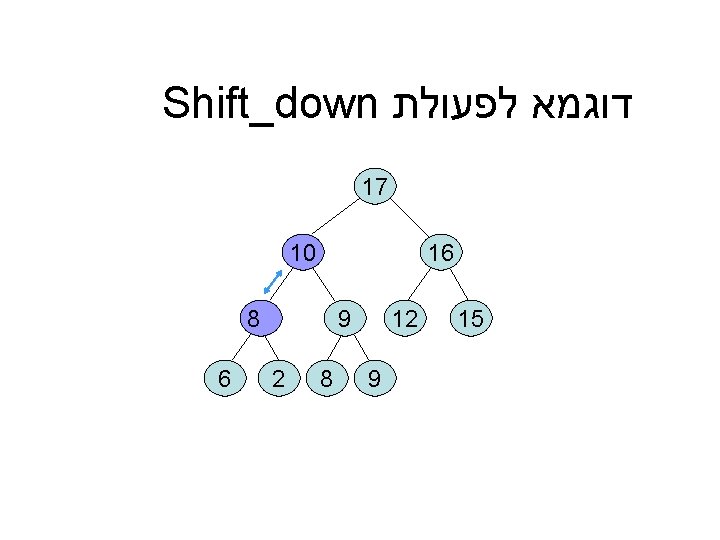
דוגמא לפעולת Shift_down 17 16 15 10 12 9 9 8 8 2 6

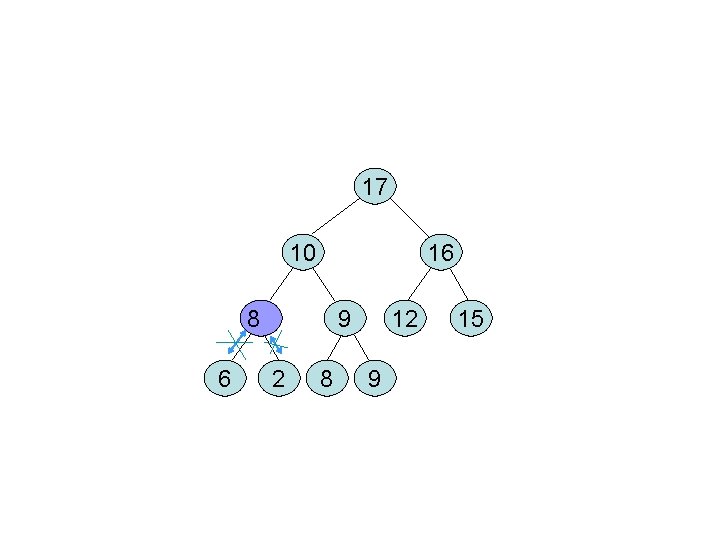
17 10 16 8 6 9 2 8 12 9 15

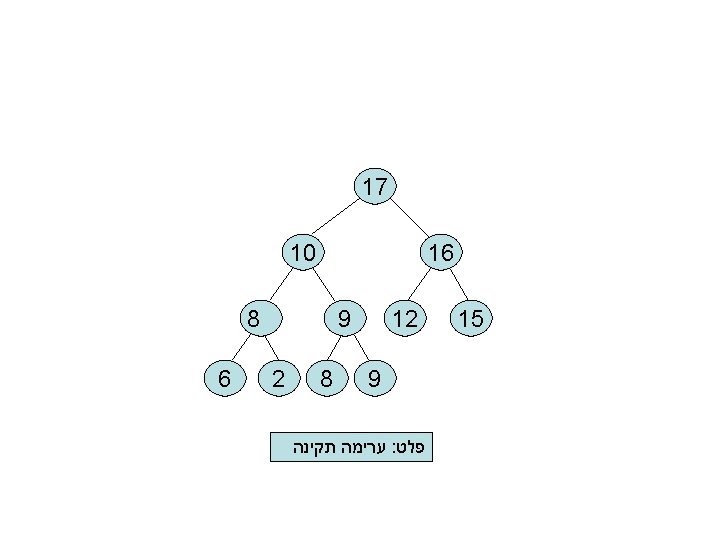
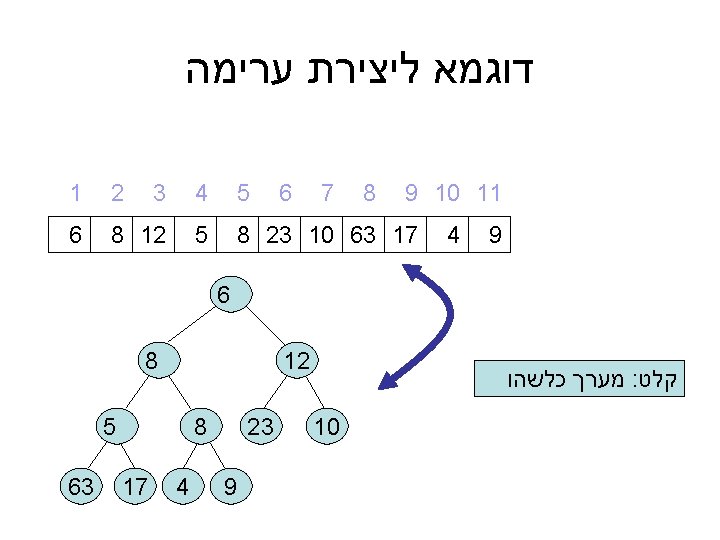
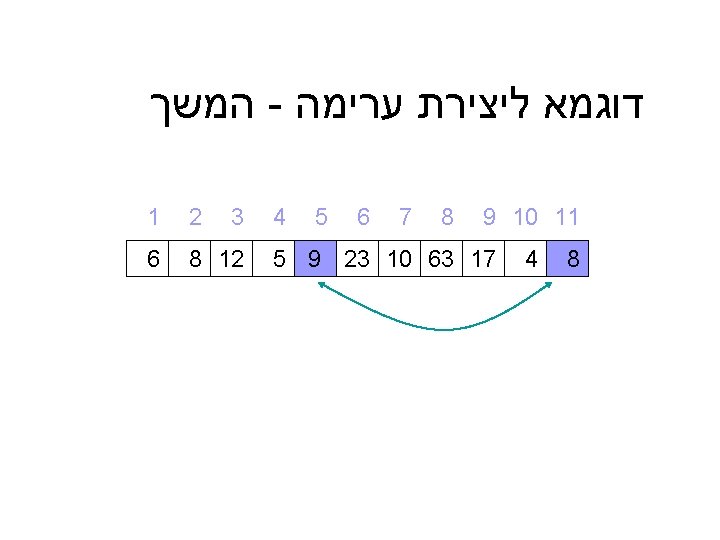
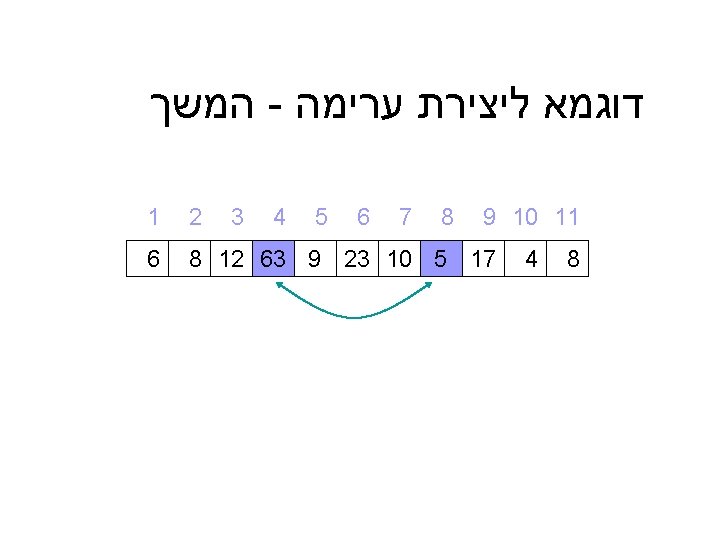
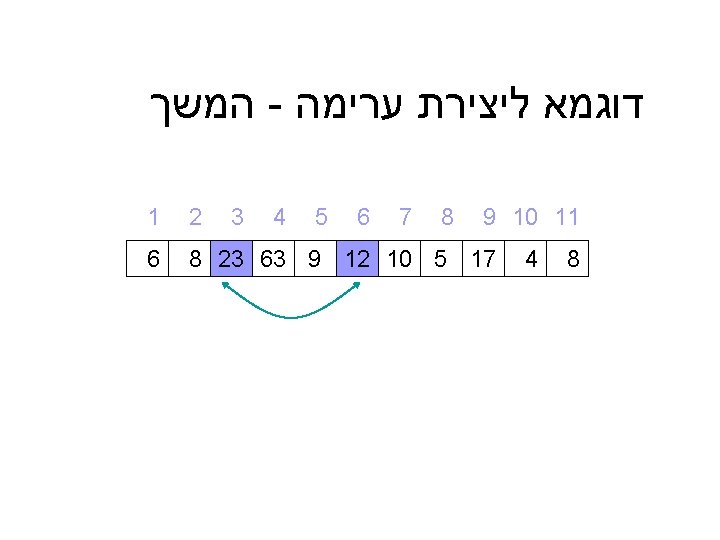
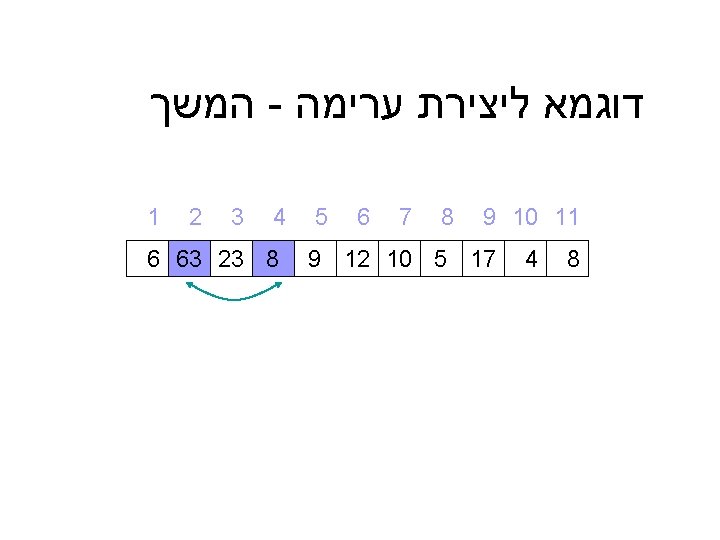
דוגמא ליצירת ערימה 9 10 11 9 4 5 4 3 2 1 8 7 6 8 23 10 63 17 5 8 12 6 6 12 קלט : מערך כלשהו 10 8 23 8 9 5 4 17 63

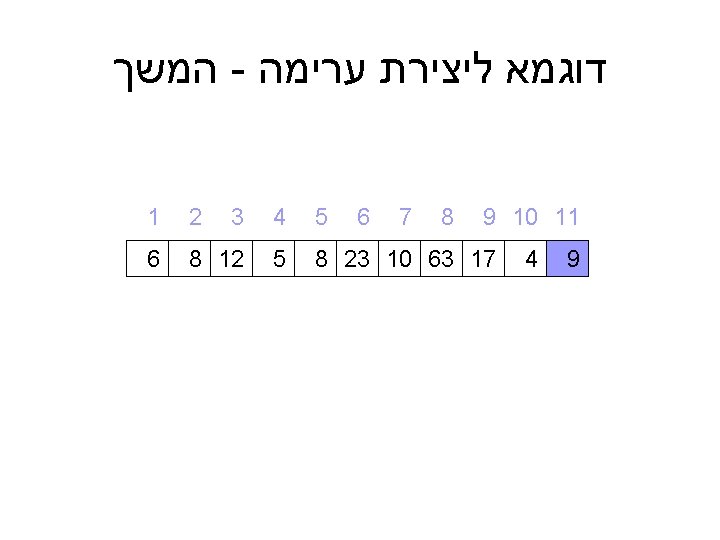
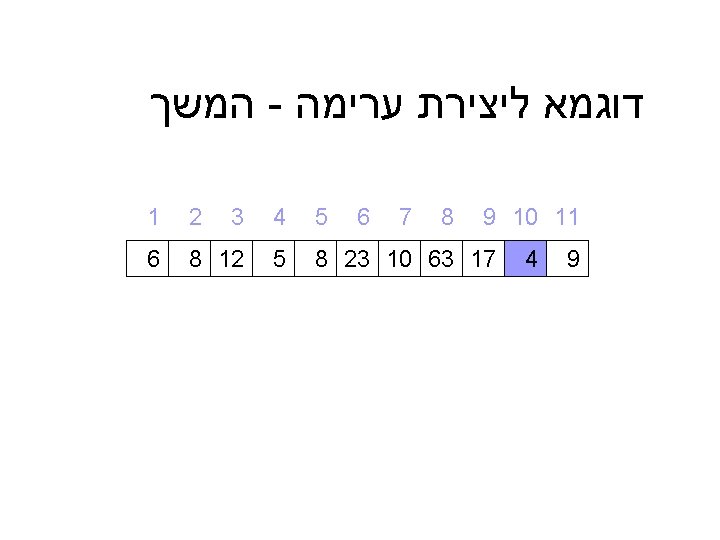
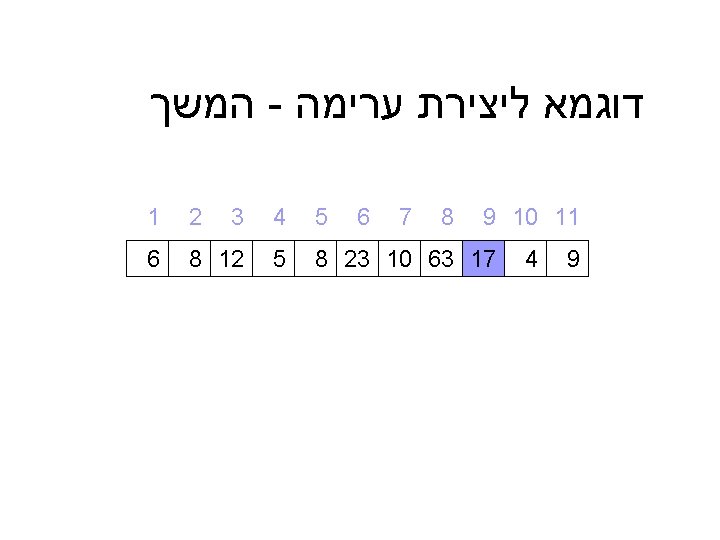
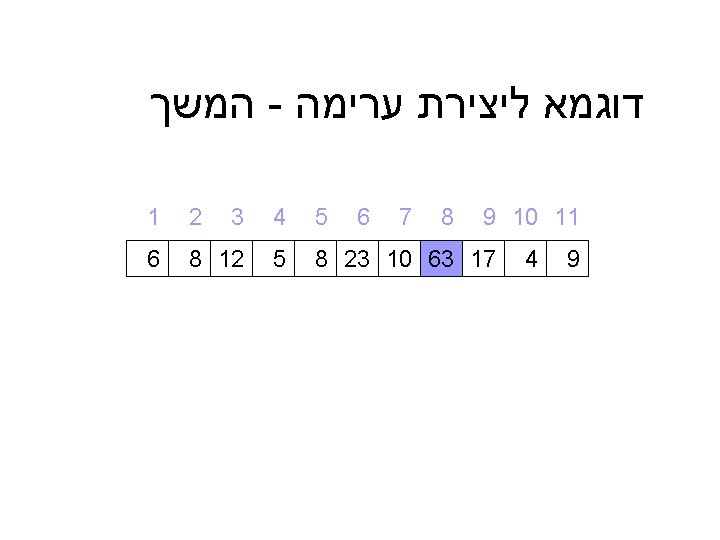
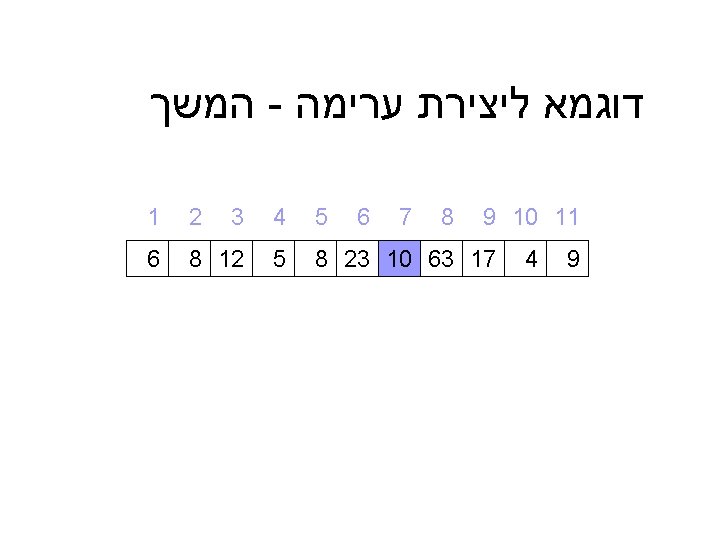
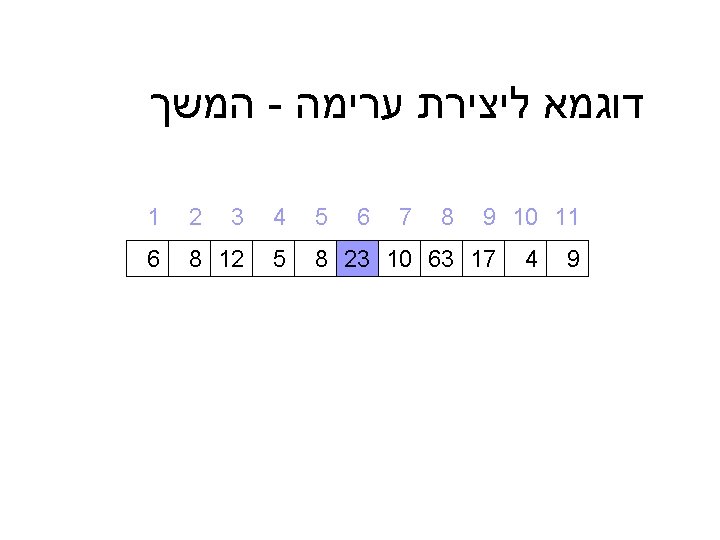
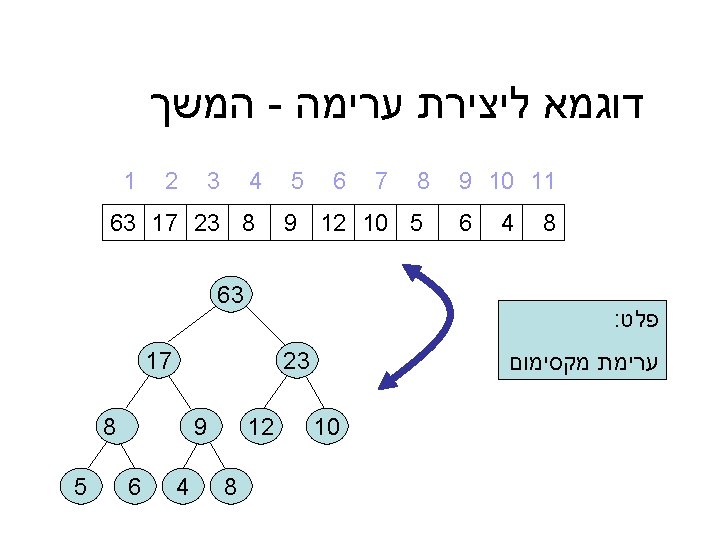
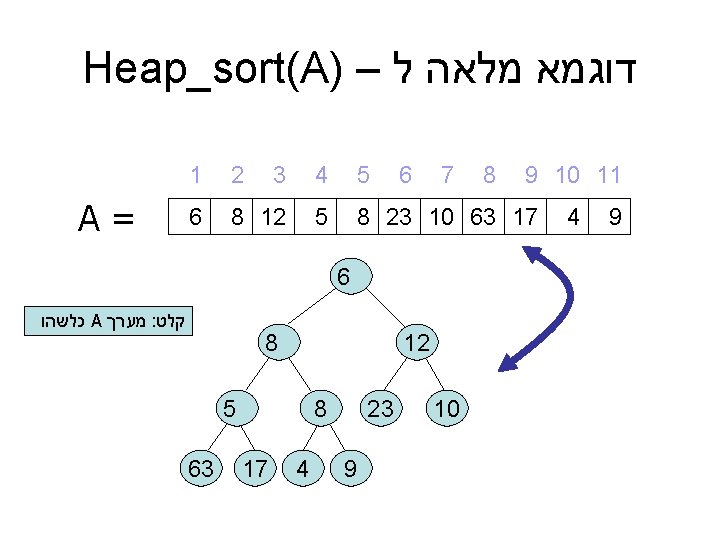
דוגמא מלאה ל – ) Heap_sort(A 9 10 11 9 4 5 4 3 2 1 8 7 6 8 23 10 63 17 5 8 12 6 = A 6 12 10 קלט : מערך A כלשהו 8 23 8 9 5 4 17 63

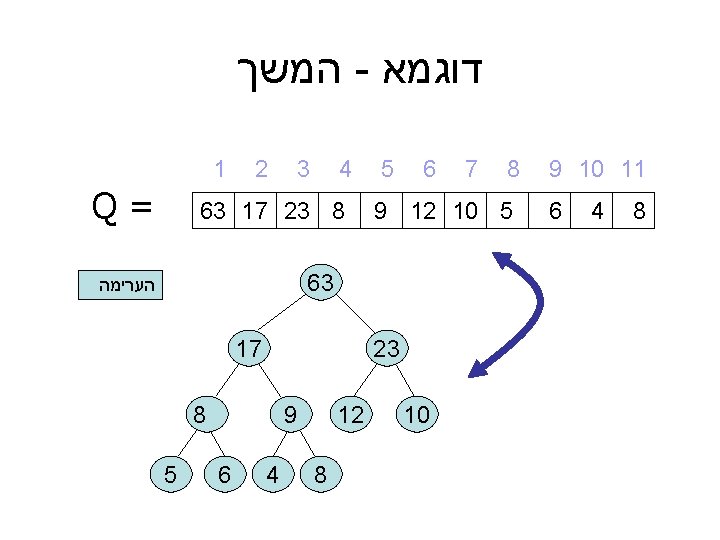
דוגמא - המשך 9 10 11 8 4 6 8 7 6 5 9 12 10 5 3 4 2 1 = Q 63 17 23 8 63 הערימה 23 10 17 12 9 8 8 4 6 5

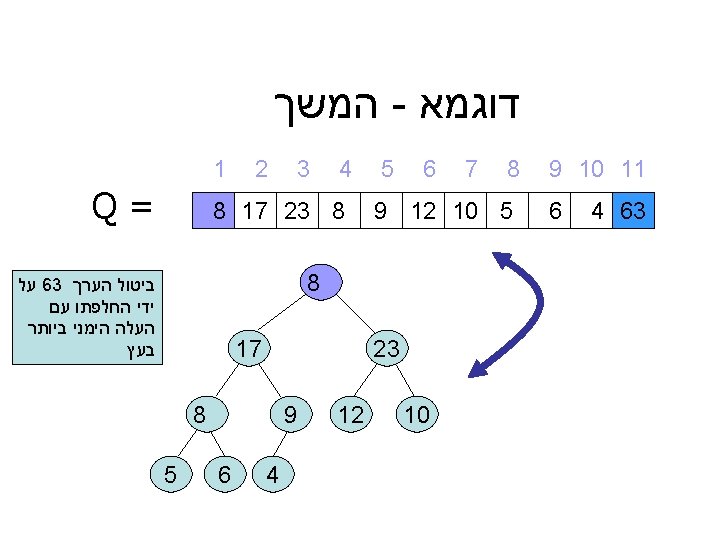
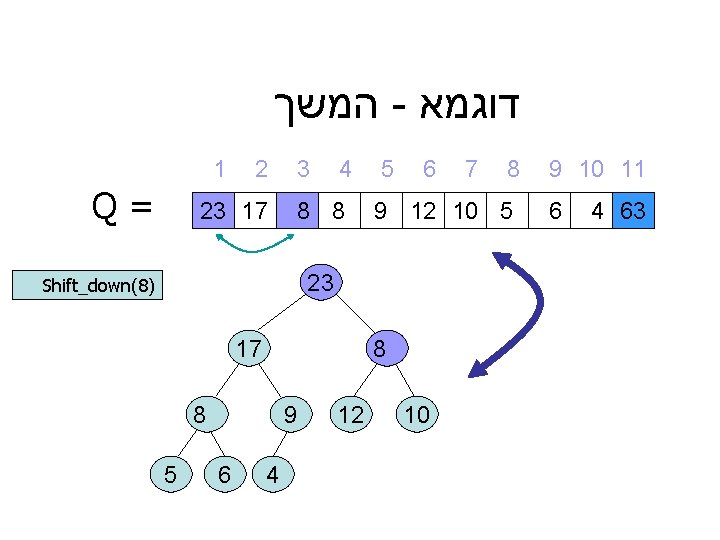
המשך - דוגמא 1 Q= 2 23 17 3 4 8 8 5 6 17 8 8 5 9 6 4 12 8 9 12 10 5 23 Shift_down(8) 7 10 9 10 11 6 4 63

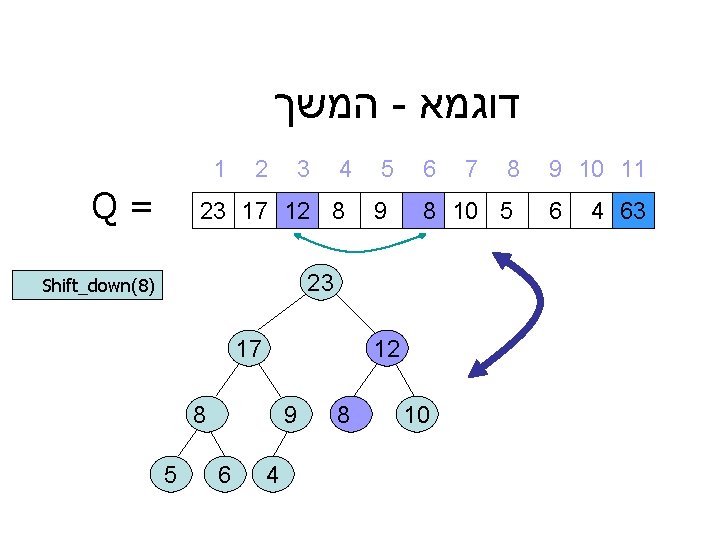
המשך - דוגמא 1 Q= 2 3 4 23 17 12 8 5 9 6 4 8 8 8 10 5 23 Shift_down(8) 7 10 9 10 11 6 4 63

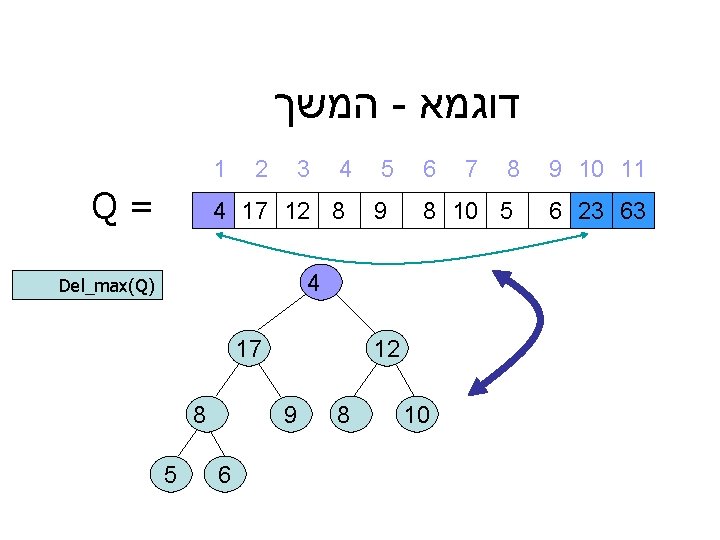
דוגמא - המשך 9 10 11 6 23 63 8 7 6 8 10 5 5 9 4 3 2 1 = Q 4 17 12 8 4 ) Del_max(Q 12 10 17 8 8 9 6 5

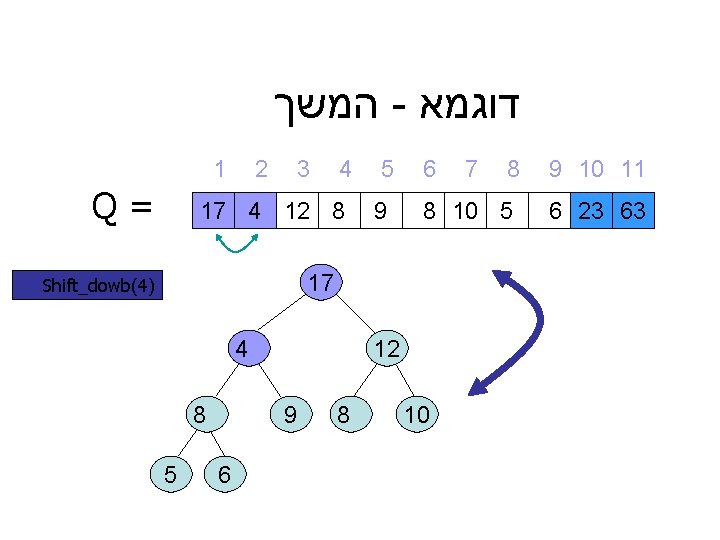
המשך - דוגמא 1 Q= 2 3 4 17 4 12 8 5 9 6 4 8 5 12 9 6 8 8 8 10 5 17 Shift_dowb(4) 7 10 9 10 11 6 23 63

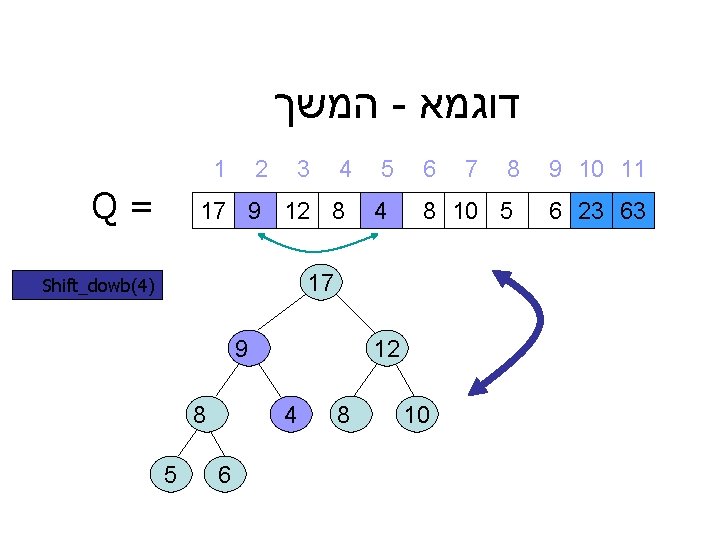
המשך - דוגמא 1 Q= 2 3 4 17 9 12 8 5 4 6 9 8 5 12 4 6 8 8 8 10 5 17 Shift_dowb(4) 7 10 9 10 11 6 23 63

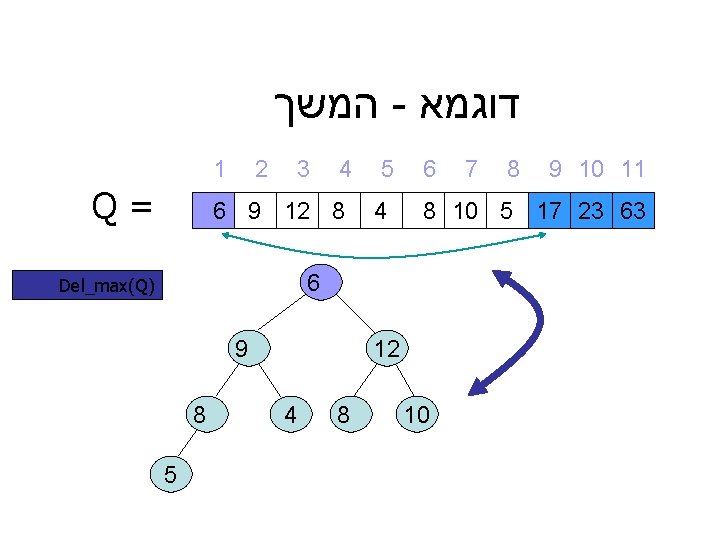
דוגמא - המשך 9 10 11 8 7 6 8 10 5 17 23 63 5 4 4 3 1 2 = Q 6 9 12 8 6 ) Del_max(Q 12 10 9 8 4 8 5

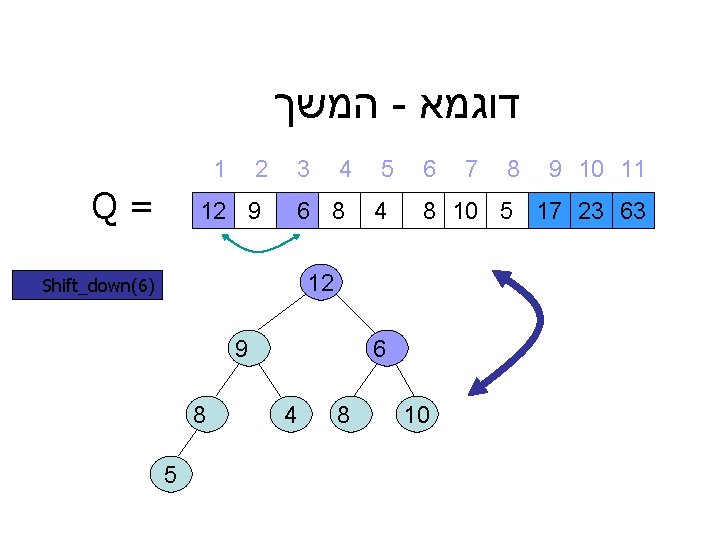
המשך - דוגמא 1 Q= 2 12 9 3 4 6 8 5 4 6 9 8 5 6 4 8 8 9 10 11 8 10 5 17 23 63 12 Shift_down(6) 7 10

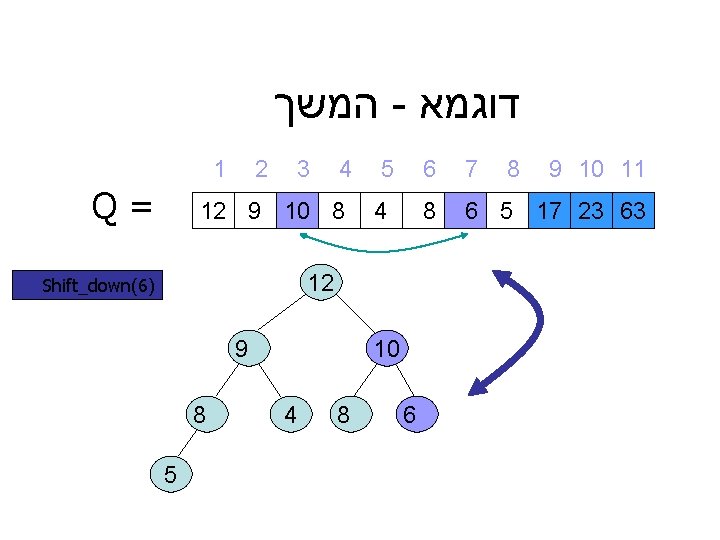
המשך - דוגמא 1 Q= 2 3 4 12 9 10 8 5 4 12 Shift_down(6) 9 8 5 10 4 8 6 6 7 8 9 10 11 8 6 5 17 23 63

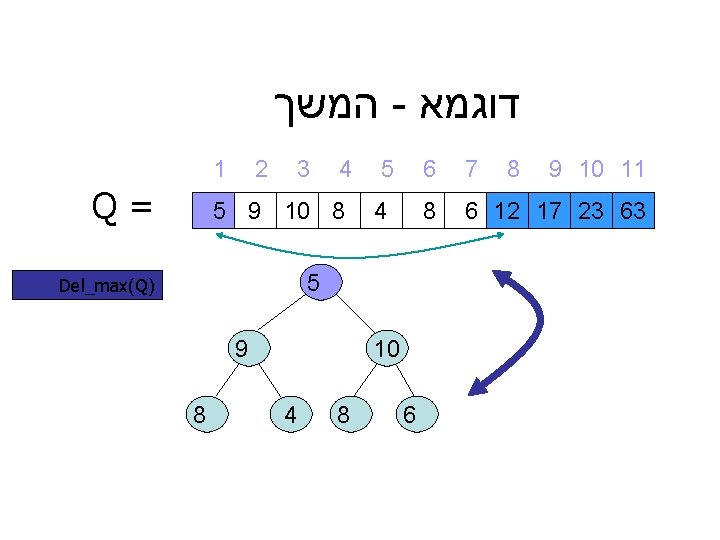
דוגמא - המשך 7 6 9 10 11 8 6 12 17 23 63 8 5 4 4 3 1 2 = Q 5 9 10 8 5 ) Del_max(Q 10 6 9 8 4 8

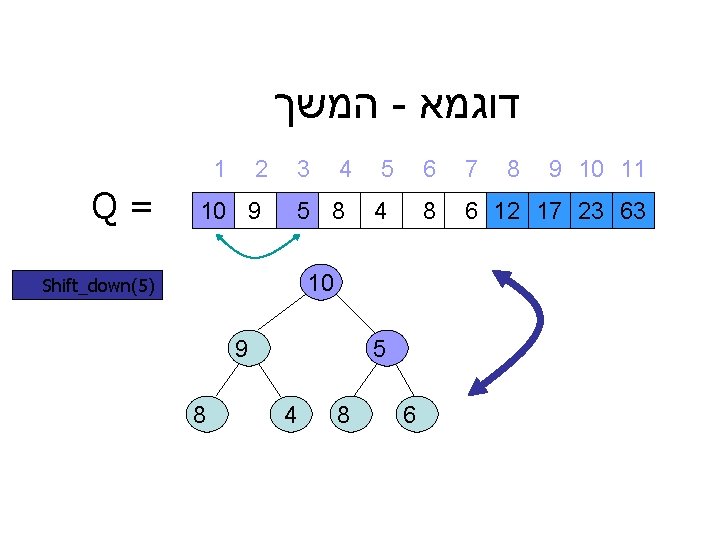
המשך - דוגמא 1 Q= 2 10 9 3 4 5 8 5 4 10 Shift_down(5) 9 8 5 4 8 6 6 7 8 9 10 11 8 6 12 17 23 63

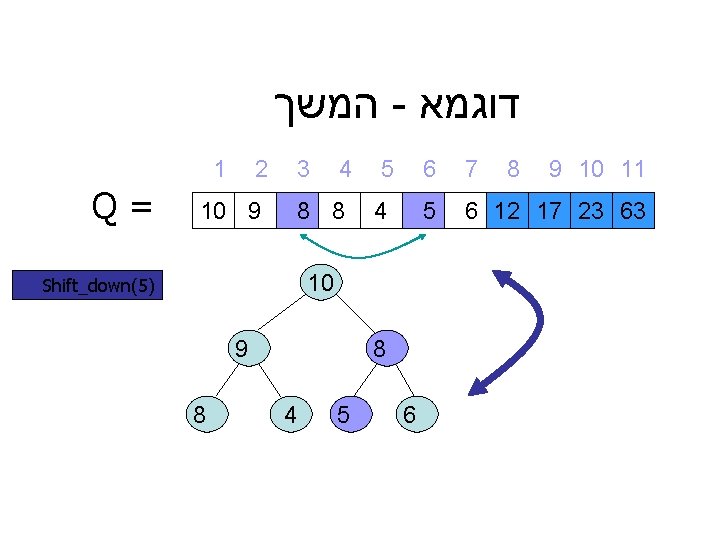
המשך - דוגמא 1 Q= 2 10 9 3 4 8 8 5 4 10 Shift_down(5) 9 8 8 4 5 6 6 7 8 9 10 11 5 6 12 17 23 63

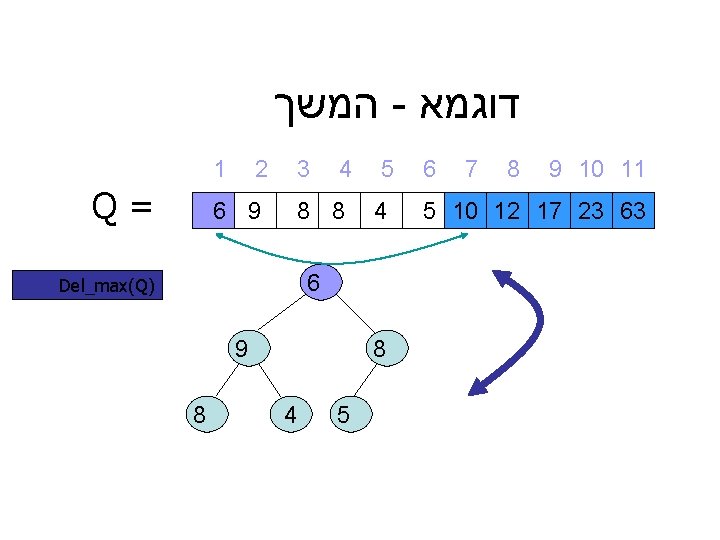
דוגמא - המשך 9 10 11 8 7 6 5 10 12 17 23 63 5 4 4 3 8 8 1 2 = Q 6 9 6 ) Del_max(Q 9 8 5 4 8

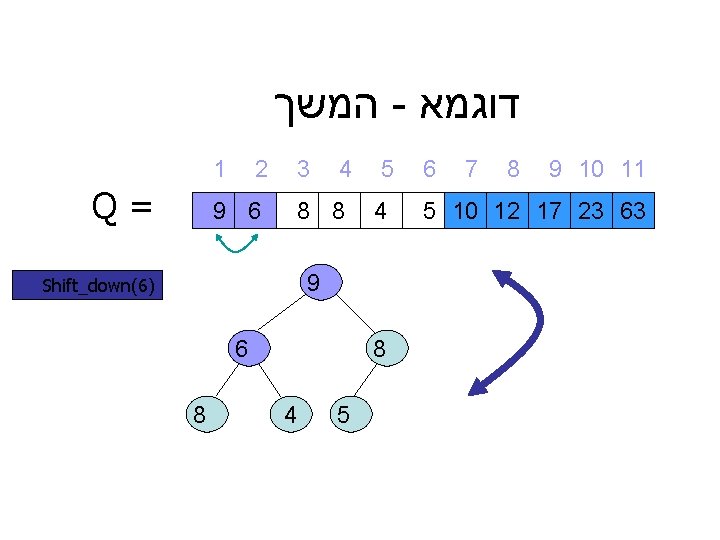
המשך - דוגמא 1 Q= 2 9 6 3 4 8 8 5 4 9 Shift_down(6) 6 8 8 4 5 6 7 8 9 10 11 5 10 12 17 23 63

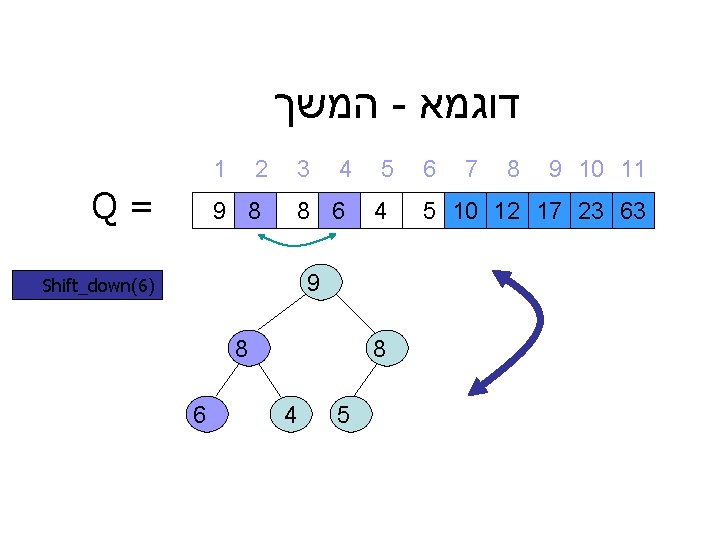
המשך - דוגמא 1 Q= 2 9 8 3 4 8 6 5 4 9 Shift_down(6) 8 6 8 4 5 6 7 8 9 10 11 5 10 12 17 23 63

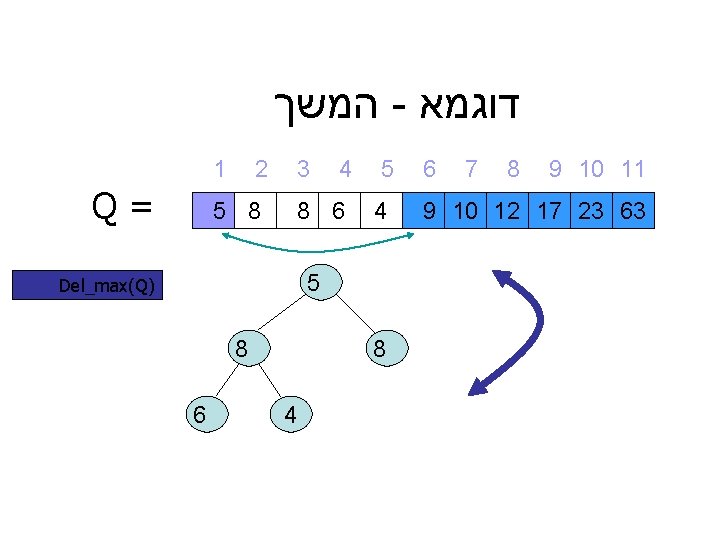
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 4 4 3 8 6 1 2 = Q 5 8 5 ) Del_max(Q 8 8 4 6

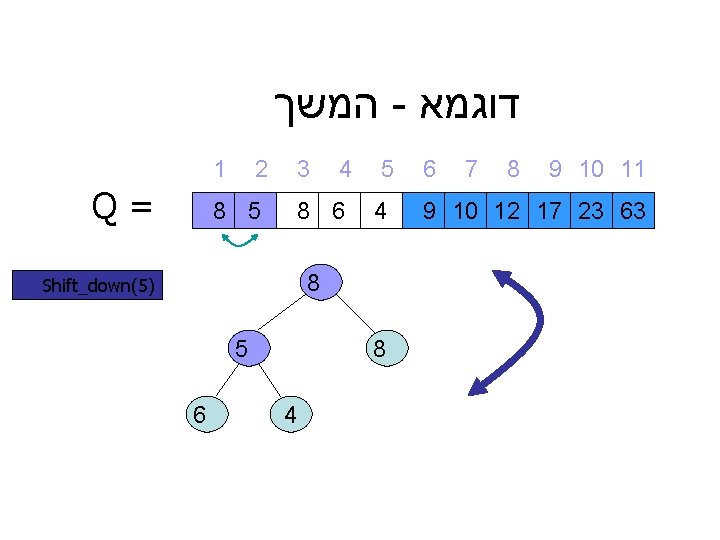
המשך - דוגמא 1 Q= 2 8 5 3 4 8 6 5 4 8 Shift_down(5) 5 6 8 4 6 7 8 9 10 11 9 10 12 17 23 63

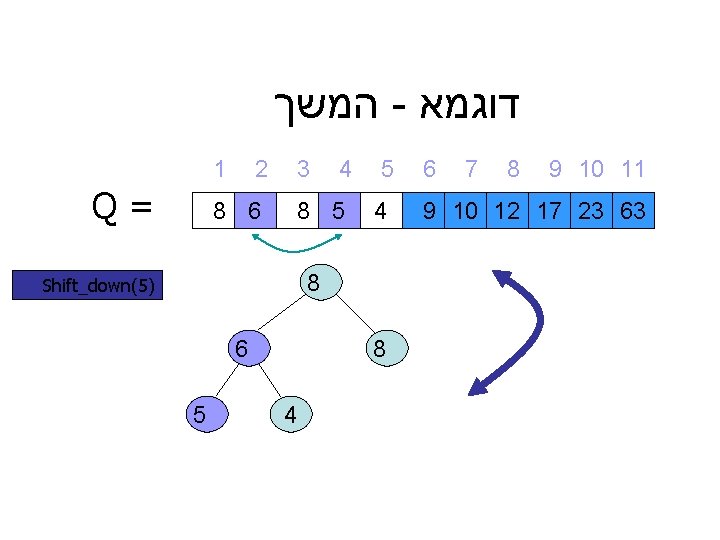
המשך - דוגמא 1 Q= 2 8 6 3 4 8 5 5 4 8 Shift_down(5) 6 5 8 4 6 7 8 9 10 11 9 10 12 17 23 63

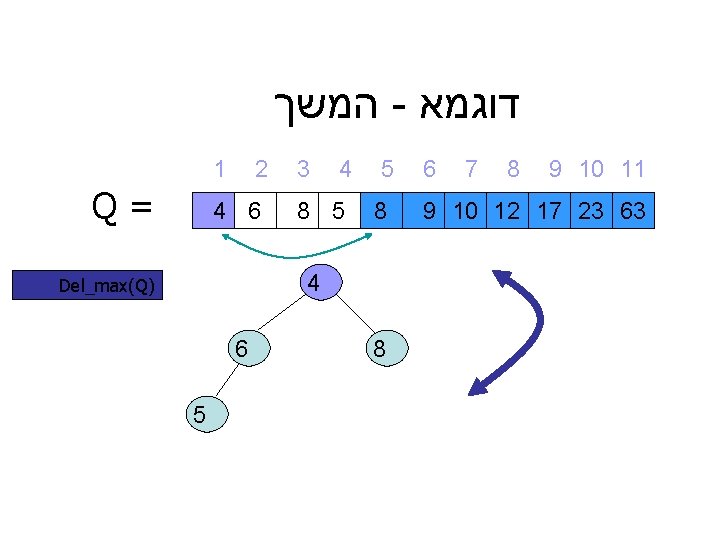
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 8 4 3 8 5 1 2 = Q 4 6 4 8 ) Del_max(Q 6 5

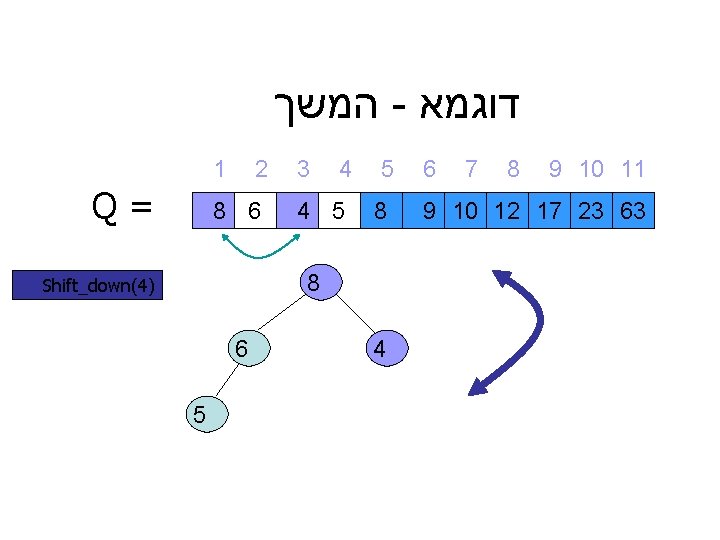
המשך - דוגמא 1 Q= 2 8 6 3 4 4 5 5 8 8 Shift_down(4) 6 5 4 6 7 8 9 10 11 9 10 12 17 23 63

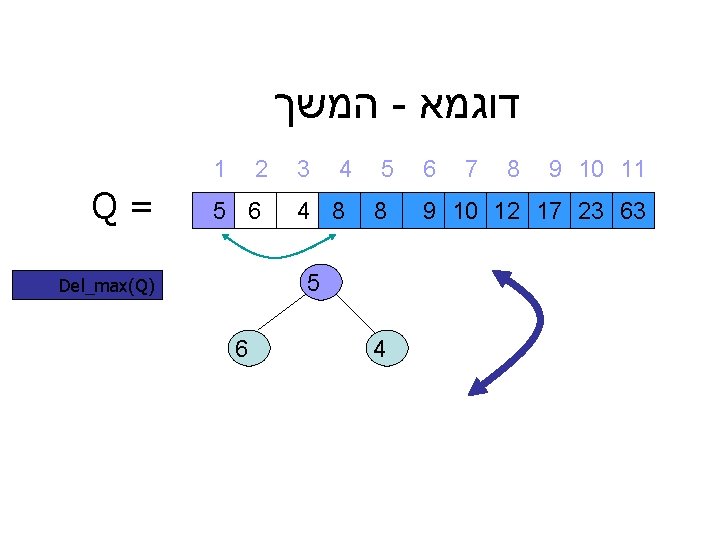
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 8 4 3 4 8 1 2 5 6 5 4 = Q ) Del_max(Q 6

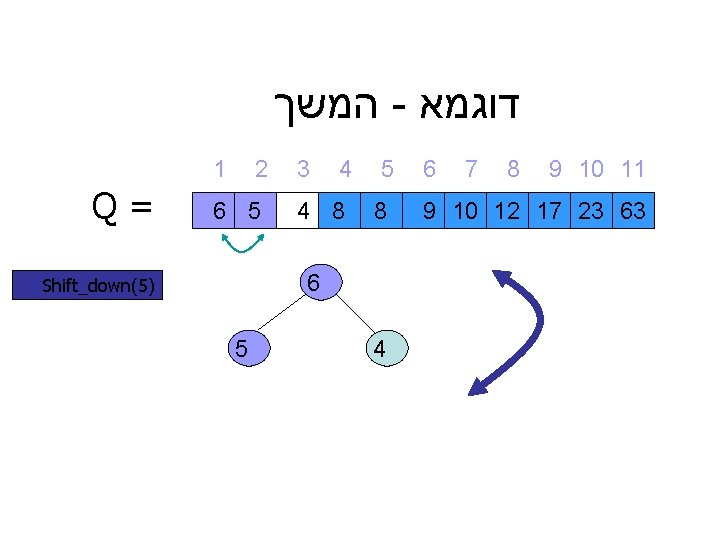
המשך - דוגמא 1 Q= 2 6 5 3 4 4 8 5 8 6 Shift_down(5) 5 4 6 7 8 9 10 11 9 10 12 17 23 63

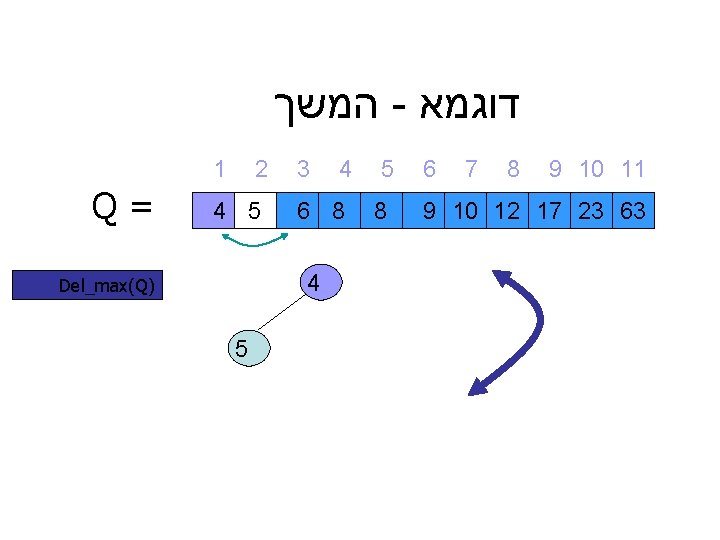
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 8 4 3 6 8 1 2 4 5 4 = Q ) Del_max(Q 5

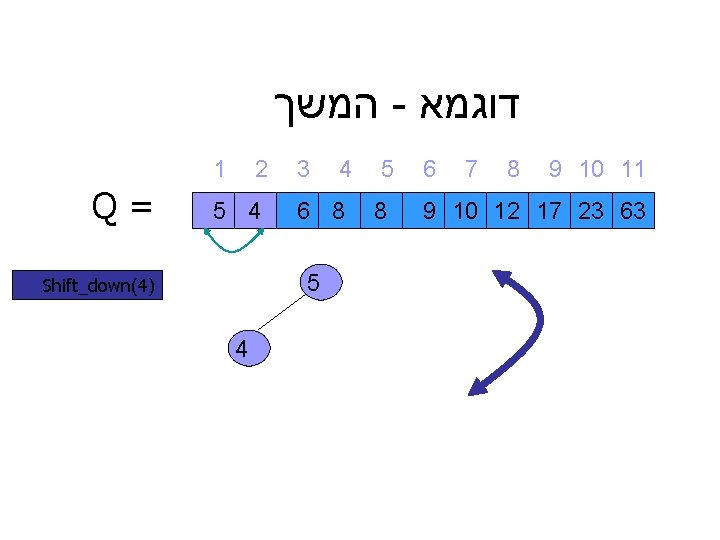
המשך - דוגמא 1 Q= 2 5 4 3 6 8 5 Shift_down(4) 4 4 5 8 6 7 8 9 10 11 9 10 12 17 23 63

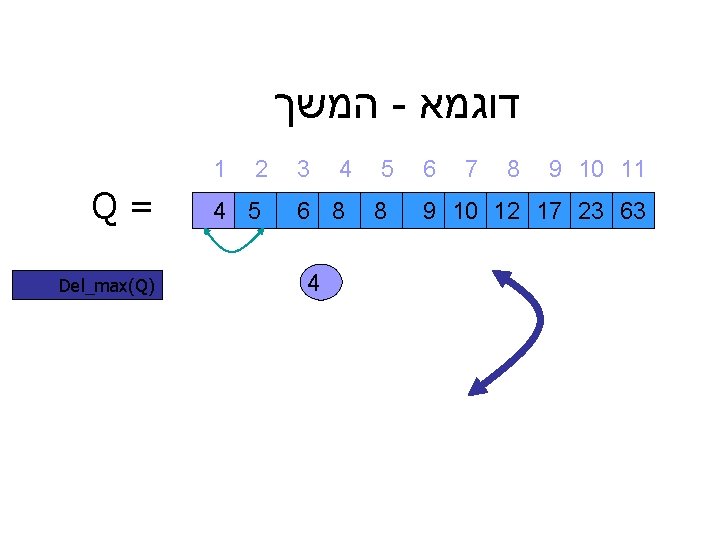
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 8 4 3 6 8 4 2 1 4 5 = Q ) Del_max(Q

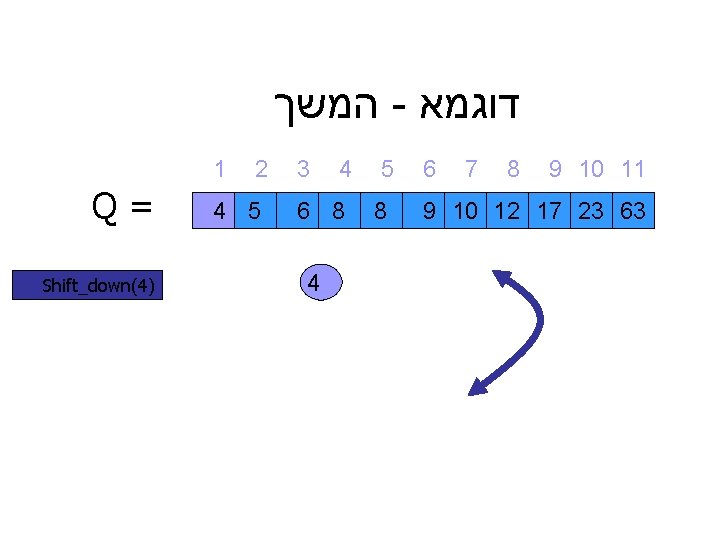
המשך - דוגמא 1 Q= Shift_down(4) 2 4 5 3 4 6 8 4 5 8 6 7 8 9 10 11 9 10 12 17 23 63

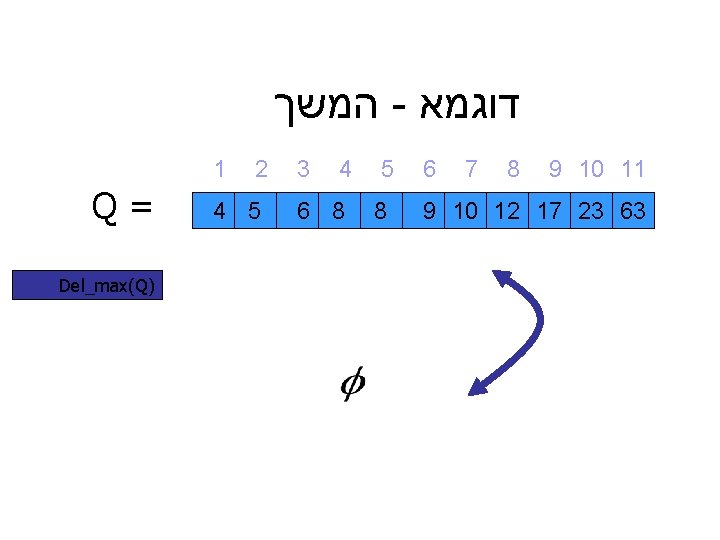
דוגמא - המשך 9 10 11 8 7 6 9 10 12 17 23 63 5 8 4 3 6 8 2 1 4 5 = Q ) Del_max(Q

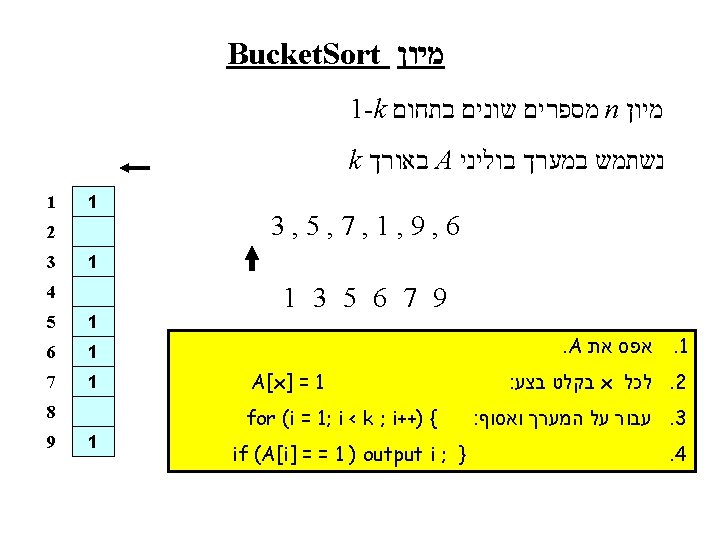
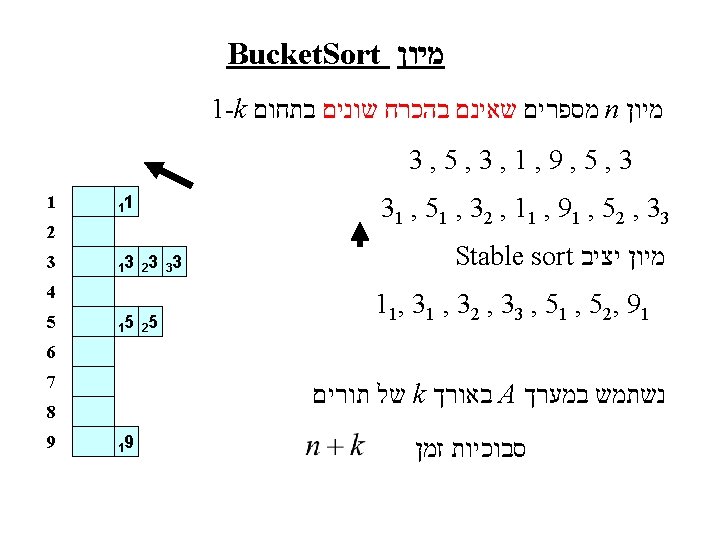
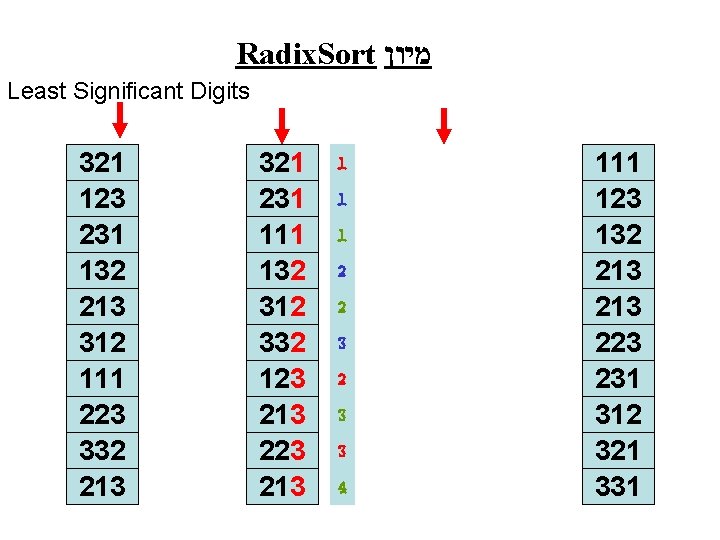
Radix. Sort מיון Least Significant Digits 321 123 231 132 213 312 111 223 332 213 321 231 111 132 312 332 123 213 223 213 1 1 1 2 2 3 3 4 111 123 132 213 223 231 312 321 331

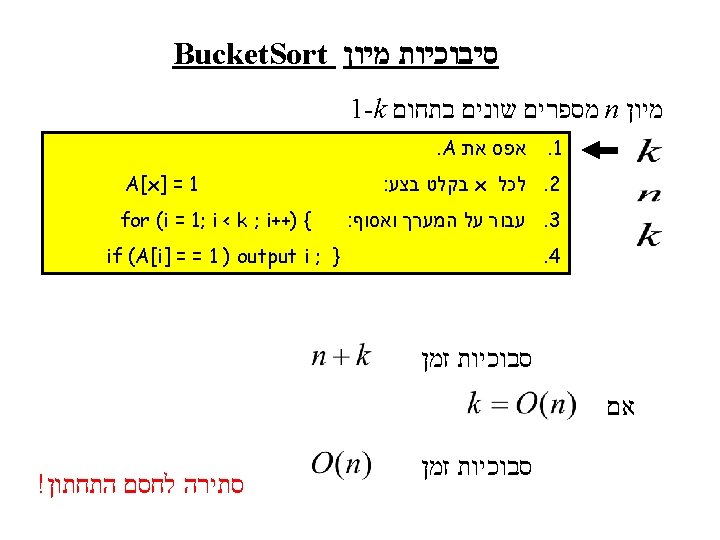
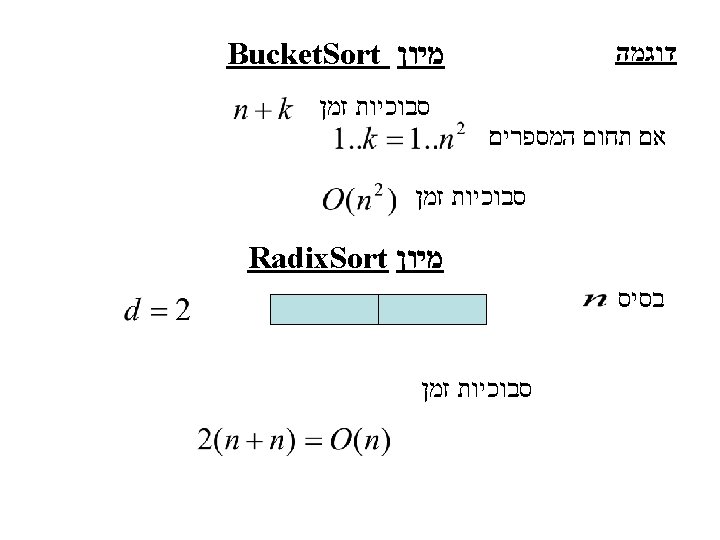
Radix. Sort מיון Radix-Sort(A, d) for i 1 to d do use Bucket. Sort to sort array A on digit i מיון מספרים Radix. Sort סבוכיות זמן אם בסיס ממין מספרים Radix. Sort