Last Time Some Visibility Hidden Surface Removal algorithms

Last Time • Some Visibility (Hidden Surface Removal) algorithms – Painter’s • Draw in some order • Things drawn later overwrite things drawn earlier – Depth Buffer • Keep a buffer that stores depth at each pixel • Overwrite pixel (and depth) if the incoming pixel is closer to the viewer 03/12/02 (c) 2002 University of Wisconsin, CS 559

Today • More Visibility Algorithms – – – 03/12/02 A-buffer Scanline method Depth Sorting Area Subdivision BSP Trees Exact 2. 5 D Visibility (c) 2002 University of Wisconsin, CS 559

Open. GL Depth Buffer • Open. GL defines a depth buffer as its visibility algorithm • The enable depth testing: gl. Enable(GL_DEPTH_TEST) • To clear the depth buffer: gl. Clear(GL_DEPTH_BUFFER_BIT) – To clear color and depth: gl. Clear(GL_COLOR_BUFFER_BIT|GL_DEPTH_BUFFER_BIT) • The number of bits used for the depth values can be specified (windowing system dependent, and hardware may impose limits based on available memory) • The comparison function can be specified: gl. Depth. Func(…) 03/12/02 (c) 2002 University of Wisconsin, CS 559
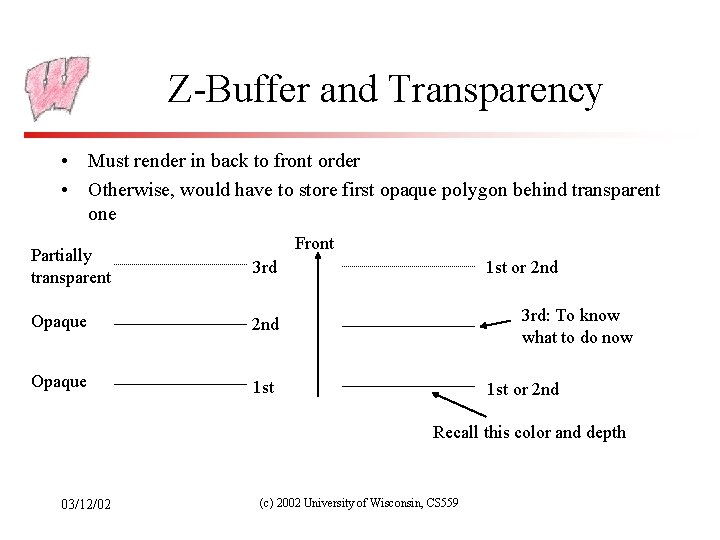
Z-Buffer and Transparency • Must render in back to front order • Otherwise, would have to store first opaque polygon behind transparent one Front Partially transparent 3 rd Opaque 2 nd Opaque 1 st or 2 nd 3 rd: To know what to do now 1 st or 2 nd Recall this color and depth 03/12/02 (c) 2002 University of Wisconsin, CS 559

The A-buffer (Image Precision) • Handles transparent surfaces and a form of anti-aliasing • At each pixel, maintain a list of polygons sorted by depth, and a sub-pixel coverage mask for each polygon – Sub-pixel mask: Matrix of bits saying which parts of the pixel are covered by the polygon • Algorithm: When drawing a pixel (first pass): – if polygon is opaque and covers pixel, insert into list, removing all polygons farther away – if polygon is transparent or only partially covers pixel, insert into list, but don’t remove farther polygons 03/12/02 (c) 2002 University of Wisconsin, CS 559

The A-buffer (2) • Algorithm: Rendering pass – At each pixel, traverse buffer using polygon colors and coverage masks to composite: over = • Advantage: – Can do more than Z-buffer • Anti-aliasing, transparent surfaces without ordering – Coverage mask idea can be used in other visibility algorithms • Disadvantages: – Not in hardware, and slow in software – Still at heart a z-buffer: Over-rendering and depth quantization problems 03/12/02 (c) 2002 University of Wisconsin, CS 559

Scan Line Algorithm (Image Precision) • Assume polygons do not intersect one another – Except maybe at edges or vertices • Observation: across any given scan line, the visible polygon can change only at an edge • Algorithm: – fill all polygons simultaneously – at each scan line, have all edges that cross scan line in AEL – keep record of current depth at current pixel - use to decide which is in front in filling span 03/12/02 (c) 2002 University of Wisconsin, CS 559
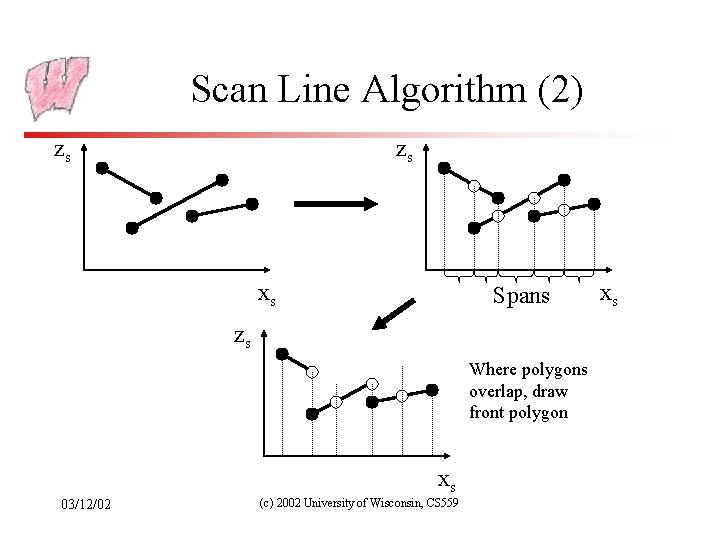
Scan Line Algorithm (2) zs zs xs Spans zs Where polygons overlap, draw front polygon xs 03/12/02 (c) 2002 University of Wisconsin, CS 559 xs

Scan Line Algorithm (3) • Advantages: – – Simple Potentially fewer quantization errors (more bits available for depth) Don’t over-render (each pixel only drawn once) Filter anti-aliasing can be made to work (have information about all polygons at each pixel) • Disadvantages: – Invisible polygons clog AEL, ET – Non-intersection criteria may be hard to meet 03/12/02 (c) 2002 University of Wisconsin, CS 559

Depth Sorting (Object Precision, in view space) • • An example of a list-priority algorithm Sort polygons on depth of some point Render from back to front (modifying order on the fly) Rendering: For surface S with greatest depth – If no overlap in depth with other polygons, scan convert – Else, for overlaps in depth, test for overlaps in the image plane • If none, scan convert and go to next polygon – If S, S’ overlap in depth and in image plane, swap order and try again – If S, S’ have been swapped already, split and reinsert 03/12/02 (c) 2002 University of Wisconsin, CS 559
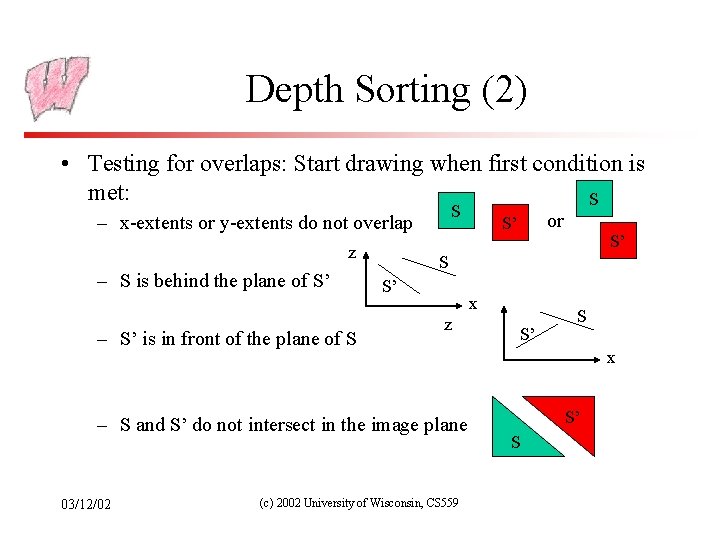
Depth Sorting (2) • Testing for overlaps: Start drawing when first condition is met: S S – x-extents or y-extents do not overlap z – S is behind the plane of S’ – S’ is in front of the plane of S S’ x z – S and S’ do not intersect in the image plane 03/12/02 or S’ (c) 2002 University of Wisconsin, CS 559 S’ S x S’ S

Depth sorting • Advantages: – Filter anti-aliasing works fine • Composite in back to front order with a sequence of over operations – No depth quantization error • Depth comparisons carried out in high-precision view space • Disadvantages: – Over-rendering – Potentially very large number of splits - (n 2) fragments from n polygons 03/12/02 (c) 2002 University of Wisconsin, CS 559

Area Subdivision • • Exploits area coherence: Small areas of an image are likely to be covered by only one polygon Three easy cases for determining what’s in front in a given region: 1. 2. 3. 03/12/02 a polygon is completely in front of everything else in that region no surfaces project to the region only one surface is completely inside the region, overlaps the region, or surrounds the region (c) 2002 University of Wisconsin, CS 559

Warnock’s Area Subdivision (Image Precision) • • • Start with whole image If one of the easy cases is satisfied (previous slide), draw what’s in front Otherwise, subdivide the region and recurse If region is single pixel, choose surface with smallest depth Advantages: – No over-rendering – Anti-aliases well - just recurse deeper to get sub-pixel information • Disadvantage: – Tests are quite complex and slow 03/12/02 (c) 2002 University of Wisconsin, CS 559
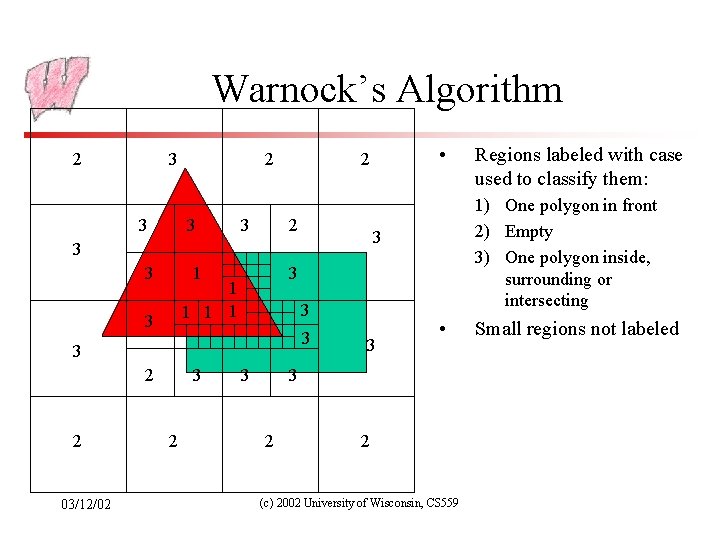
Warnock’s Algorithm 2 3 3 2 1 3 1 1 3 3 2 2 03/12/02 3 3 • 3 2 Regions labeled with case used to classify them: 1) One polygon in front 2) Empty 3) One polygon inside, surrounding or intersecting 3 3 3 • 2 2 (c) 2002 University of Wisconsin, CS 559 Small regions not labeled

BSP-Trees (Object Precision) • Construct a binary space partition tree – Tree gives a rendering order – A list-priority algorithm • Tree splits 3 D world with planes – The world is broken into convex cells – Each cell is the intersection of all the half-spaces of splitting planes on tree path to the cell • Also used to model the shape of objects, and in other visibility algorithms – BSP visibility in games does not necessarily refer to this algorithm 03/12/02 (c) 2002 University of Wisconsin, CS 559
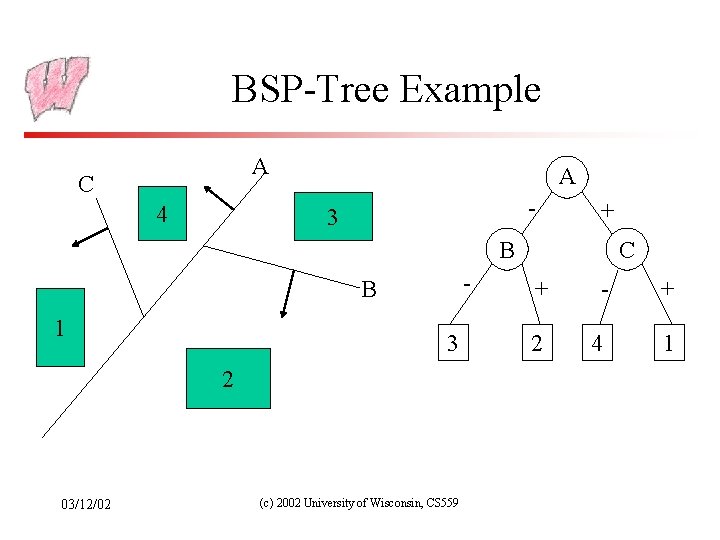
BSP-Tree Example A C 4 A - 3 + C B - B 1 3 2 03/12/02 (c) 2002 University of Wisconsin, CS 559 + - + 2 4 1

Building BSP-Trees • Choose polygon (arbitrary) • Split its cell using plane on which polygon lies – May have to chop polygons in two (Clipping!) • Continue until each cell contains only one polygon fragment • Splitting planes could be chosen in other ways, but there is no efficient optimal algorithm for building BSP trees – Optimal means minimum number of polygon fragments in a balanced tree 03/12/02 (c) 2002 University of Wisconsin, CS 559
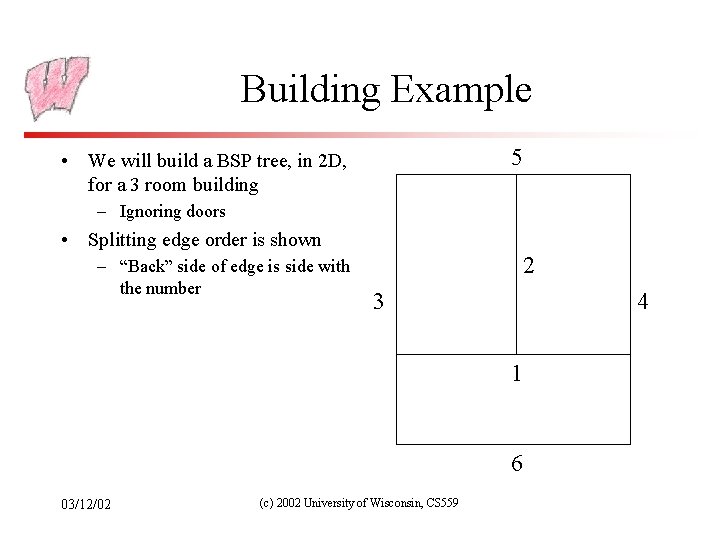
Building Example 5 • We will build a BSP tree, in 2 D, for a 3 room building – Ignoring doors • Splitting edge order is shown – “Back” side of edge is side with the number 2 3 4 1 6 03/12/02 (c) 2002 University of Wisconsin, CS 559
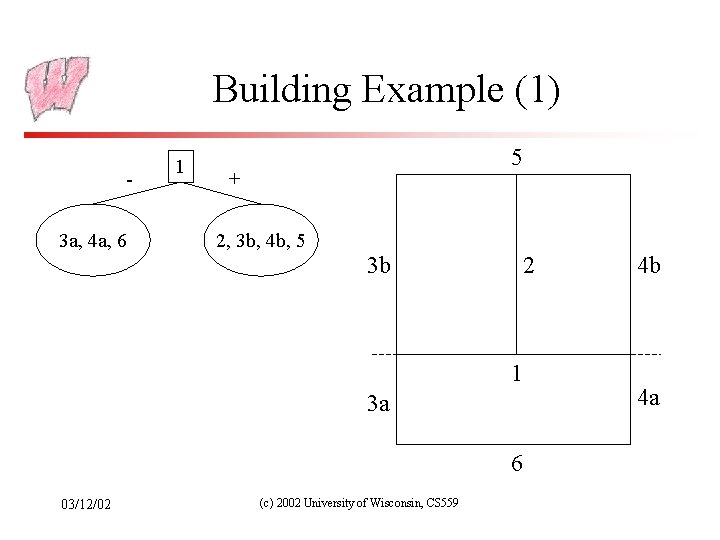
Building Example (1) 3 a, 4 a, 6 1 5 + 2, 3 b, 4 b, 5 3 b 2 1 3 a 6 03/12/02 (c) 2002 University of Wisconsin, CS 559 4 b 4 a
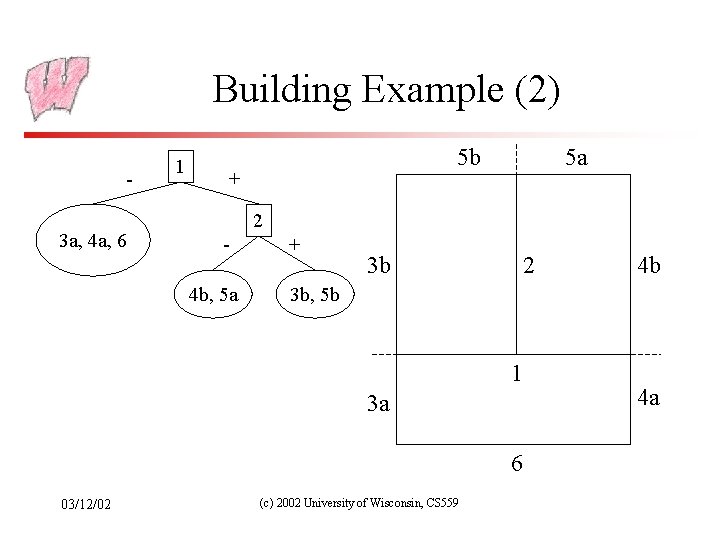
Building Example (2) 3 a, 4 a, 6 1 5 b + 5 a 2 4 b, 5 a + 3 b 2 3 b, 5 b 1 3 a 6 03/12/02 4 b (c) 2002 University of Wisconsin, CS 559 4 a
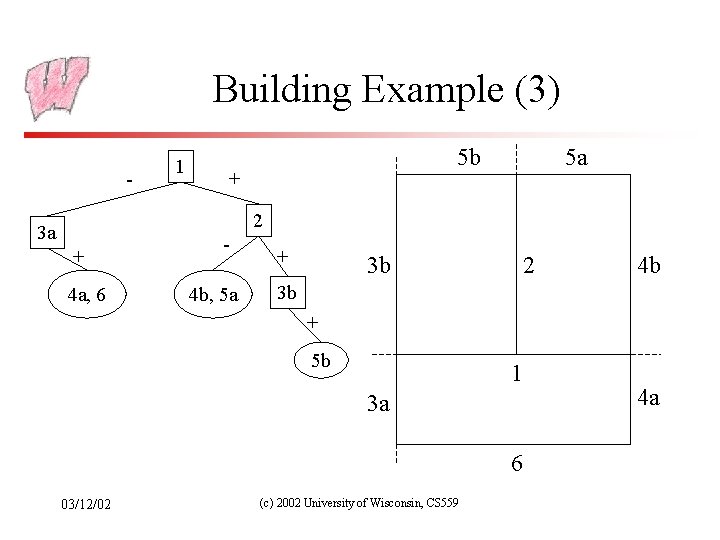
Building Example (3) - 1 5 b + 5 a 2 3 a + 4 a, 6 4 b, 5 a + 3 b 2 4 b 3 b + 5 b 1 3 a 6 03/12/02 (c) 2002 University of Wisconsin, CS 559 4 a
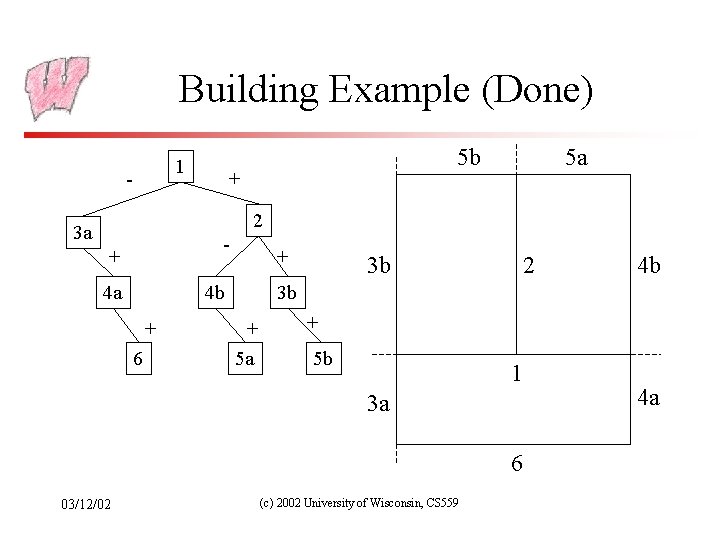
Building Example (Done) 1 - 5 b + 5 a 2 3 a - + 4 a + 4 b + 6 3 b 2 3 b + 5 a + 5 b 1 3 a 6 03/12/02 4 b (c) 2002 University of Wisconsin, CS 559 4 a
- Slides: 23