Last Time Meshing Volume Scattering Radiometry Adsorption and

Last Time • Meshing • Volume Scattering Radiometry (Adsorption and Emission) 02/25/05 © 2005 University of Wisconsin

Today • Participating Media – Scattering theory – Integrating Participating Media 02/25/05 © 2005 University of Wisconsin

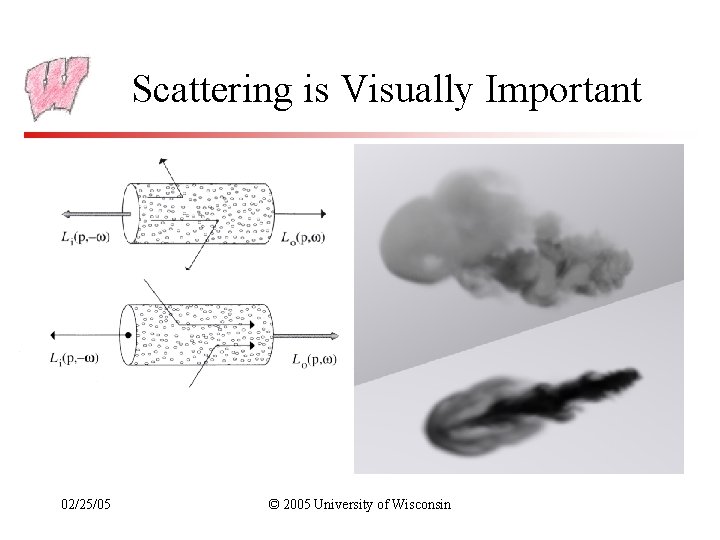
Scattering • Particles in the media act as little reflectors – They are too small to see, but they influence the light passing through • Scattering has two effects – Out-scattering: light along a line is scattered in a different direction – In-scattering: light from some other direction is scattered into the direction of interest • Out-scattering decreases radiance, in-scattering increases it 02/25/05 © 2005 University of Wisconsin

Scattering is Visually Important 02/25/05 © 2005 University of Wisconsin

Out-Scattering Math • There is an out-scattering co-efficient s (p, ) – The probability density that light is scattered per unit distance – Just like absorption coefficient, but it’s not being converted, it’s being redirected • Define attenuation coefficient: t= a+ s • Define transmittance, Tr, between two points: 02/25/05 © 2005 University of Wisconsin

Transmittance Properties • Transmittance from a point to itself is 1 • Transmittance multiplies along a ray – In a voxel-based volume, we can compute transmittance through each voxel and multiply to get total through volume 02/25/05 © 2005 University of Wisconsin

Optical Thickness • Define optical thickness, : • If the medium is homogeneous, t does not depend on p – Integration is easy and we get Beer’s law 02/25/05 © 2005 University of Wisconsin

Phase Function • We need a function that tells us what directions light gets scattered in – The participating media equivalent of the BRDF • The phase function, p( ’), gives the distribution of outgoing directions, ’, for an incoming direction, – A probability distribution, so it must be normalized over the hemisphere: 02/25/05 © 2005 University of Wisconsin

In-Scattering • The phase function tells us where light gets scattered • To find out how much light gets scattered into a direction, integrate over all the directions it could be scattered from Proportion Incoming scattered into radiance direction 02/25/05 © 2005 University of Wisconsin

Source Term • Given the emission radiance and the phase function, we can define a source term, S – The total amount of radiance added per unit length – Note the resemblance to the surface scattering equation 02/25/05 © 2005 University of Wisconsin

Isotropic vs. Anisotropic Media • A medium is isotropic if the phase function depends only on the angle between the directions, – Write p(cos ) • Most natural materials are like this, except crystal structures • Phase functions are also reciprocal: p( ’)=p( ’ ) 02/25/05 © 2005 University of Wisconsin

Isotropic vs. Anisotropic Phase Functions • A phase function is isotropic if it scatters equally in all directions: pisotropic( ’)=const • There is only one possible isotropic phase function – Why? What is the additional constraint on phase functions? • Homogeneous/inhomogeneous refers to spatial variation, isotropic/anisotropic refers to directional variation 02/25/05 © 2005 University of Wisconsin

Physically-Based Phase Functions • Two common physically-based formulas • Air molecules are modeled by Rayleigh scattering – Optical extinction coefficient varies with -4 – What phenomena does this explain? • Scattering due to larger particles (dust, water droplets) is modeled with Mie scattering – Scattering depends less on wavelength, so what color is haze? • Turbidity is a useful measurement: T=(tm+th)/tm – tm is vertical optical thickness of molecular atmosphere – th is vertical optical thickness of haze atmosphere 02/25/05 © 2005 University of Wisconsin

Henyey-Greenstein Function • Single parameter, g, controls relative proportion of forward/backward scattering: g (0, 1) 02/25/05 © 2005 University of Wisconsin

Alternatives • Linear combination of Henyey-Greenstein – Weights must sum to 1 to keep normalized • Schlick Approximation – Avoid 3/2 power computation – k roughly 1. 55 g-. 55 g 3 02/25/05 © 2005 University of Wisconsin

Sampling Henyey-Greenstein • Because of the isotropic medium assumption, the distribution is separable into one for and one for • Given 1 and 2: • Given an incoming direction, use these to generate a scattered direction 02/25/05 © 2005 University of Wisconsin

PBRT Volume Models • PBRT volumes must give – – Extent (3 D shape to intersect) Functions to return scattering parameters Function to return phase function at a point Function to compute optical thickness between two points • Simplest is homogeneous volume – Everything is constant, and optical thickness comes from Beer’s law 02/25/05 © 2005 University of Wisconsin

Homogeneous Medium 02/25/05 © 2005 University of Wisconsin

Homogeneous with Varying Density • Assume that the same medium is present, but that the density varies • All parameters are scaled by density – Except optical thickness, which may be hard to compute • Options: – 3 D Grids – give sampled density on grid and interpolate – Exponential density from some ground plane: – Aggregates of volumes 02/25/05 © 2005 University of Wisconsin

Exponential Height Fog 02/25/05 © 2005 University of Wisconsin

Computing Optical Thickness • Recall: • Obviously we can use: • The best way to get the T(j) is to use stratified sampling with a fixed offset – The offset is different for each query, but fixed among the T(j) T(5) t 0 u 02/25/05 t 1 © 2005 University of Wisconsin

Equation of Transfer • Radiance arriving is radiance leaving a surface that is attenuated plus radiance that gets in-scattered and emitted on the way from the surface – The transmittance describes the out-scattering and adsorption – The source term describes the emission and in-scattering 02/25/05 © 2005 University of Wisconsin

Solving Transfer Equation • The hard part is the integral – Transmittance is simple – it depends only on optical thickness, which we just saw how to compute – Implementation increases step for transfer that is NOT to the camera • Several possible assumptions in the integral – Emission only – simple because radiance from other directions is not required – Single-scattering only – simple because only radiance from light sources is considered – Multiple – hard because you have to account for radiance from all directions, including other scattering events, so it blows up 02/25/05 © 2005 University of Wisconsin

Emission Only • Choose points through the volume to evaluate emission • Attenuate via transmittance • Sum over points in Monte Carlo: – Point are chosen using uniform offset stratified sampling (a few slides back) within the part of the ray that the volume occupies – The transmittance can be computed cumulatively as we step along the ray 02/25/05 © 2005 University of Wisconsin

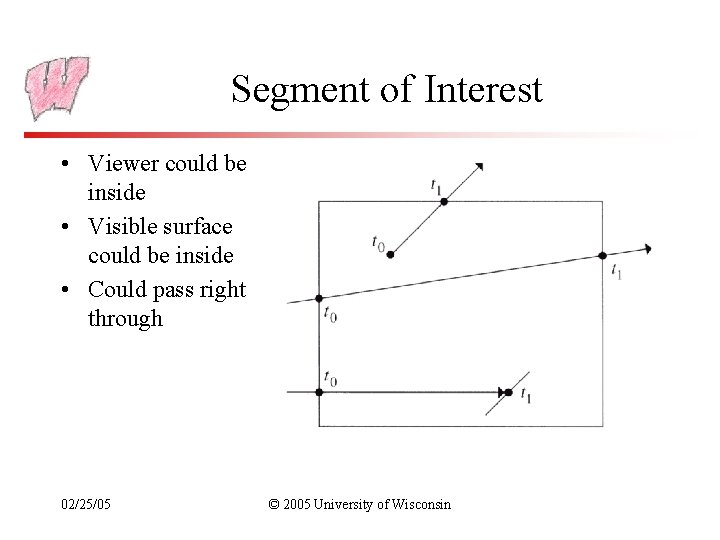
Segment of Interest • Viewer could be inside • Visible surface could be inside • Could pass right through 02/25/05 © 2005 University of Wisconsin

Cumulative Transmittance 02/25/05 © 2005 University of Wisconsin

Emission Example 02/25/05 © 2005 University of Wisconsin

Single Scattering • Evaluates • Very similar to previous slide, except: – At each point, sample light sources and push through phase function to get and estimate of the inner integral – Have to account for transmittance between light and sample point – Actually, only sample one light for each sample point along the ray 02/25/05 © 2005 University of Wisconsin

Single Scattering Example 02/25/05 © 2005 University of Wisconsin

Multiple Scattering • Can do it like path sampling – At each point along ray, sample multiple outgoing directions – For each sampled direction, find first hit surface • Add in outgoing radiance from that surface – itself expensive to compute – For ray to first hit surface, recursively apply the algorithm • Account for scattering within the volume into this dircection • Very computationally inefficient • Speedups: Bi-Directional, Volumetric Photon Mapping 02/25/05 © 2005 University of Wisconsin

Next Time • Sky models • Sub-surface scattering 02/25/05 © 2005 University of Wisconsin