Last Time Electrostatic Phenomena Coulombs Law force between

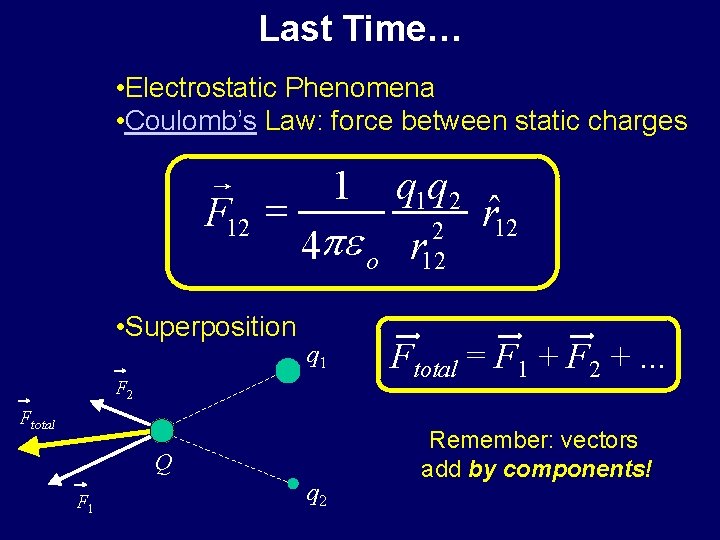
Last Time… • Electrostatic Phenomena • Coulomb’s Law: force between static charges r F 12 = • Superposition 1 q 1 q 2 ˆ r 12 2 4 pe o r 12 q 1 F 2 Ftotal Q F 1 q 2 Ftotal = F 1 + F 2 +. . . Remember: vectors add by components!

Today. . . • Define Electric Field in terms of force on a test charge • How to think about fields • Electric Field Lines • Example Calculation: Electric Dipoles
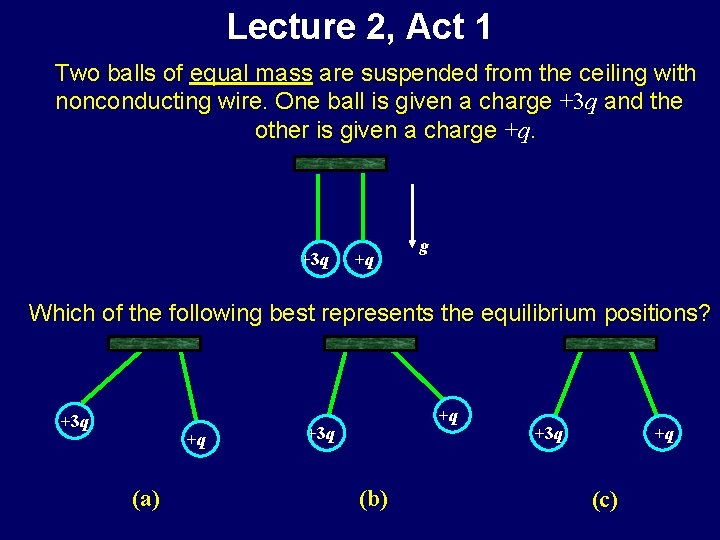
Lecture 2, Act 1 Two balls of equal mass are suspended from the ceiling with nonconducting wire. One ball is given a charge +3 q and the other is given a charge +q. +3 q +q g Which of the following best represents the equilibrium positions? +3 q +q (a) +q +3 q (b) +3 q +q (c)

Lecture 2, Act 1 Which best represents the equilibrium position? +3 q +q (a) +q +3 q (b) +q +3 q (c) • Remember Newton’s Third Law! • The force on the +3 q charge due to the +q charge must be equal and opposite to the force of the +3 q charge on the +q charge • Amount of charge on each ball determines the magnitude of the force, but each ball experiences the same magnitude of force • Symmetry, therefore, demands (c) P. S. Knowing the form of Coulomb’s law you can write two equations with two unknowns (T and q )

Preflight 2: Two charges q = + 1 μC and Q = +10 μC are placed near each other as shown in the figure. 6) Which of the following diagrams best describes the forces acting on the charges: +1 μC a) b) c) +10 μC

The Electric Field • A simple, yet profound observation - The net Coulomb force on a given charge is always proportional to the strength of that charge. q 1 F 2 F F = F 1 + F 2 Q F 1 q 2 r F= Q æç q 1 rˆ1 q 2 rˆ2 ö÷ + 2 ÷ 2 ç 4 pe 0 è r 1 r 2 ø test charge - We can now define a quantity, the electric field, which is independent of the test charge, Q, and depends only on position in space: r r F The qi are the sources º E of the electric field Q

The Electric Field r r F E º Q With this concept, we can “map” the electric field anywhere in space produced by any arbitrary: Charge Distribution Collection of Point Charges F=QE + + - - + - Test charge Q + + +++ + “Net” E at origin These charges or this charge distribution are the “source” of the electric field throughout space

Example: Electric Field What is the electric field at the origin due to this set of charges? 1) Notice that the fields from the top-right and bottom left cancel at the origin? y a +q a a 2) The electric field, then, is just the field from the top -left charge. It points away a from the top-left charge as shown. +q 3) Magnitude of E-field at the origin is: kq E= 2 2 a The x and y components of the field at (0, 0) are: kq cosq kq sinq = Ex = E y 2 a 2 kq 1 = 2 = -2 a 2 2 +q a Q x

Example: Electric Field Now, a charge, Q, is placed at the origin. What is the net force y on that charge? a a +q +q q 1 Ex = k 2 a a 2 a 2 a x Q +q If the test charge Q is positive, the force will be in the direction of the electric field If the test charge Q is negative, the force will be against the direction of the electric field F is

Let’s Try Some Numbers. . . If q = 5 m. C, a = 5 cm, and Q = 15 m. C. Then Ex = 6. 364 106 N/C and Ey = -6. 364 106 N/C a +q a x Fx = QEx and Fy = QEy So. . . Fx= 95. 5 N and y a Fy= -95. 5 N +q We also know that the magnitude of E = 9. 00 106 N/C We can, therefore, calculate the magnitude of F F = |Q| E = 135 N

Lecture 2, Act 2 Two charges, q 1 and q 2, fixed along the x-axis as shown produce an electric field, E, at a point (x, y)=(0, d) which is directed along the negative y-axis. d - Which of the following is true? (a) Both charges q 1 and q 2 are positive q 1 (b) Both charges q 1 and q 2 are negative (c) The charges q 1 and q 2 have opposite signs y E q 2 x

Lecture 2, Act 2 Two charges, q 1 and q 2, fixed along the x-axis as shown produce an electric field, E, at a point (x, y)=(0, d) which is directed along the negative y-axis. d - Which of the following is true? (a) Both charges q 1 and q 2 are positive q y E q 2 1 x (b) Both charges q 1 and q 2 are negative (c) The charges q 1 and q 2 have opposite signs E E E q 1 q 2 (a) q 1 q 2 (b) q 1 q 2 (c)

Reality of Electric Fields • The electric field has been introduced as a mathematical convenience, just as the gravitational field of Physics 111 • There is MUCH MORE to electric fields than this! IMPORTANT FEATURE: E field propagates at speed of light • NO instantaneous action at a distance (we will explain this when we discuss electromagnetic waves) • i. e. , as charge moves, resultant E-field at time t depends upon where charge was at time t - dt • For now, we avoid these complications by restricting ourselves to situations in which the source of the E-field is at rest. (electrostatics)
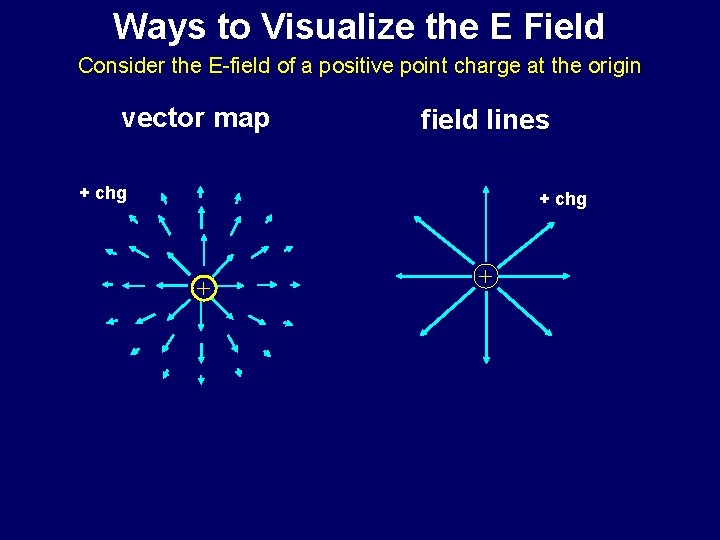
Ways to Visualize the E Field Consider the E-field of a positive point charge at the origin vector map field lines + chg + +

Rules for Vector Maps + chg + • Direction of arrows indicates the direction of the field at each point in space • Length of arrows is proportional to the magnitude of the field at each point in space

Rules for Field Lines + graphical “trick” for visualizing E fields - • Lines leave (+) charges and return to (-) charges • Number of lines leaving/entering charge µ amount of charge • Field lines never cross → Tangent of line = direction of E at each point → Local density of field lines ~ magnitude of E at each point • Field at two white dots differs by a factor of 4 since r differs by a factor of 2 (Coulomb’s law, E ~ 1/ r 2) • Local density of field lines / unit area also differs by a factor of 4 in 3 D: same # lines spread over area ~ r 2
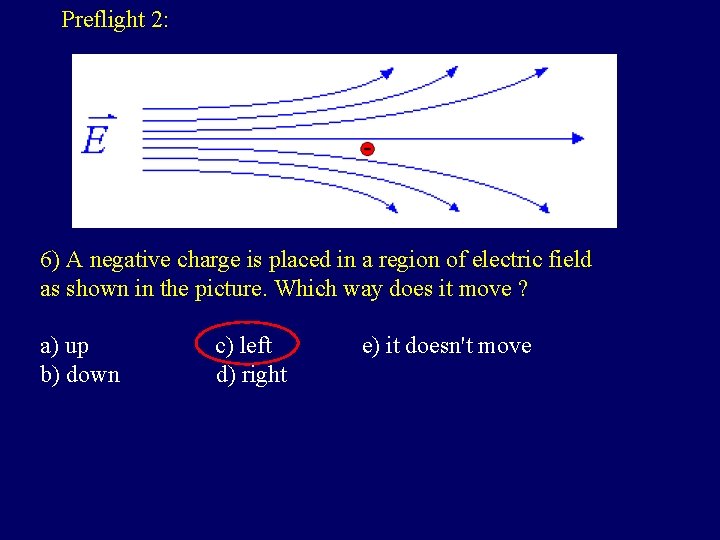
Preflight 2: 6) A negative charge is placed in a region of electric field as shown in the picture. Which way does it move ? a) up b) down c) left d) right e) it doesn't move
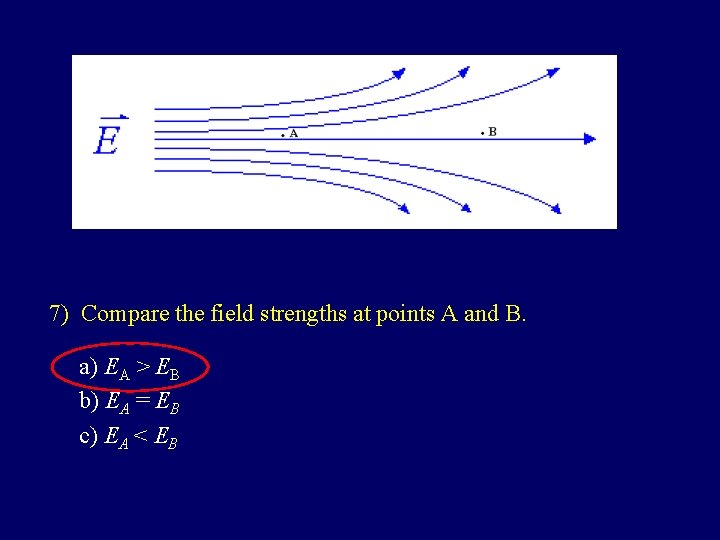
7) Compare the field strengths at points A and B. a) EA > EB b) EA = EB c) EA < EB

Lecture 2, Act 3 y • Consider a dipole (2 separated equal and opposite charges) with the y-axis as shown. -Which of the following statements about Ex(2 a, a) is true? (a) Ex(2 a, a) < 0 (b) Ex(2 a, a) = 0 +Q a a a 2 a x -Q (c) Ex(2 a, a) > 0

Lecture 2, Act 3 y • Consider a dipole (2 separated equal and opposite charges) with the y-axis as shown. -Which of the following statements about Ex(2 a, a) is true? (a) Ex(2 a, a) < 0 (b) Ex(2 a, a) = 0 Ex +Q a a a 2 a x -Q (c) Ex(2 a, a) > 0 Solution: Draw some field lines according to our rules. Falstad's Electrostatics Applets: 2 D Falstad's Electrostatics Applets: 3 D

Preflight 2: Two equal, but opposite charges are placed on the x axis. The positive charge is placed at x = -5 m and the negative charge is placed at x = +5 m as shown in the figure above. 3) What is the direction of the electric field at point A? a) up b) down c) left d) right e) zero 4) What is the direction of the electric field at point B? a) up b) down c) left d) right e) zero
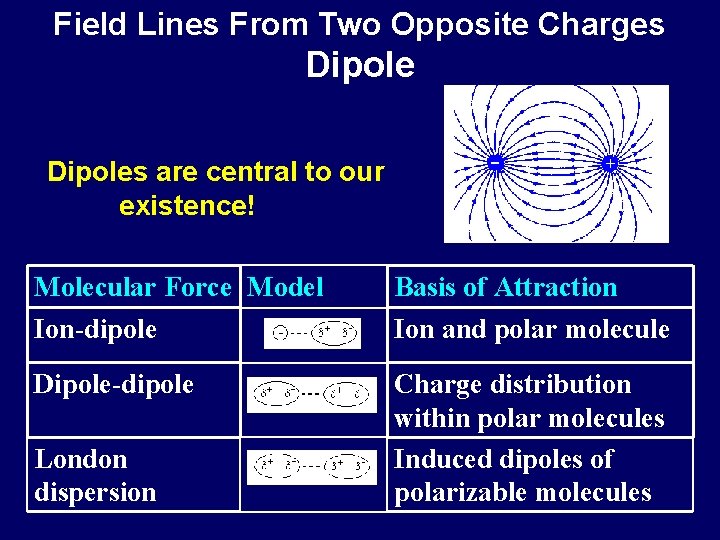
Field Lines From Two Opposite Charges Dipoles are central to our existence! Molecular Force Model Basis of Attraction Ion-dipole Ion and polar molecule Dipole-dipole Charge distribution within polar molecules Induced dipoles of polarizable molecules London dispersion

y The Electric Dipole +q see the appendix for further information a q a -q r E x E What is the E-field generated by this arrangement of charges? Calculate for a point along x-axis: (x, 0) Ex = ? ? Symmetry Ex(x, 0) = 0 Ey = ? ?
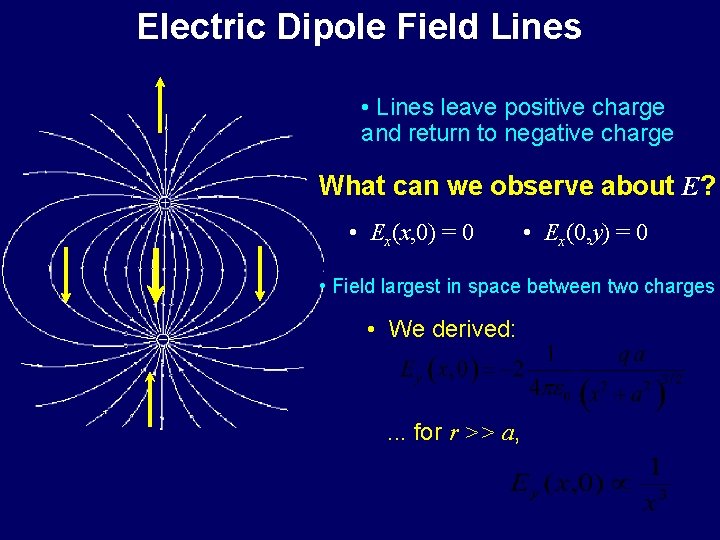
Electric Dipole Field Lines • Lines leave positive charge and return to negative charge What can we observe about E? • Ex(x, 0) = 0 • Ex(0, y) = 0 • Field largest in space between two charges • We derived: . . . for r >> a,

Field Lines From Two Like Charges • There is a zero halfway between the two charges • r >> a: looks like the field of point charge (+2 q) at origin 4

Lecture 2, ACT 4 • • Consider a circular ring with total charge +q. The charge is spread uniformly around the ring, as shown, so there is λ = q/2 p. R charge per unit length. The electric field at the origin is (a) zero (b) (c) y + ++ + + ++ R ++ + + x + ++

Lecture 2, ACT 4 • • Consider a circular ring with total charge +q. The charge is spread uniformly around the ring, as shown, so there is λ = q/2 p. R charge per unit length. The electric field at the origin is (a) zero (b) y + ++ + + ++ R ++ + + x + ++ (c) • The key thing to remember here is that the total field at the origin is given by the vector sum of the contributions from all bits of charge. • If the total field were given by the algebraic sum, then (b) would be correct (give it a try) … but we’re dealing with vectors here, not scalars! • Note that the E field at the origin produced by one bit of charge is exactly cancelled by that produced by the bit of charge diametrically opposite!! • Therefore, the VECTOR SUM of all these contributions is ZERO!!
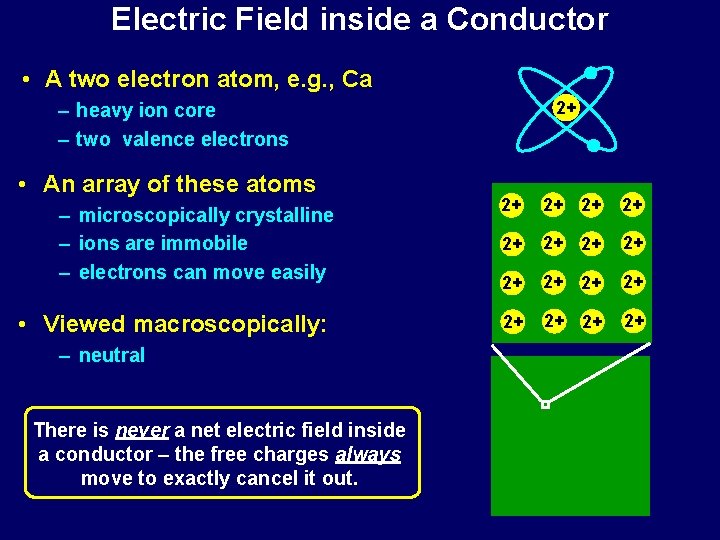
Electric Field inside a Conductor • A two electron atom, e. g. , Ca 2+ – heavy ion core – two valence electrons • An array of these atoms – microscopically crystalline – ions are immobile – electrons can move easily • Viewed macroscopically: – neutral There is never a net electric field inside a conductor – the free charges always move to exactly cancel it out. 2+ 2+ 2+ 2+

Summary • Define E-Field in terms of the force on a “test charge” • How to think about fields • Electric Field Lines • Example Calculation: Electric Dipole
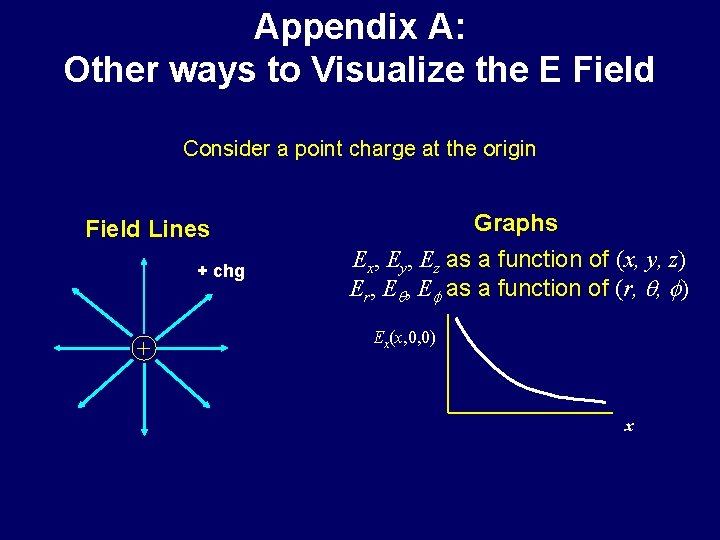
Appendix A: Other ways to Visualize the E Field Consider a point charge at the origin Field Lines + chg + Graphs Ex, Ey, Ez as a function of (x, y, z) Er, Eq, Ef as a function of (r, q, f) Ex(x, 0, 0) x
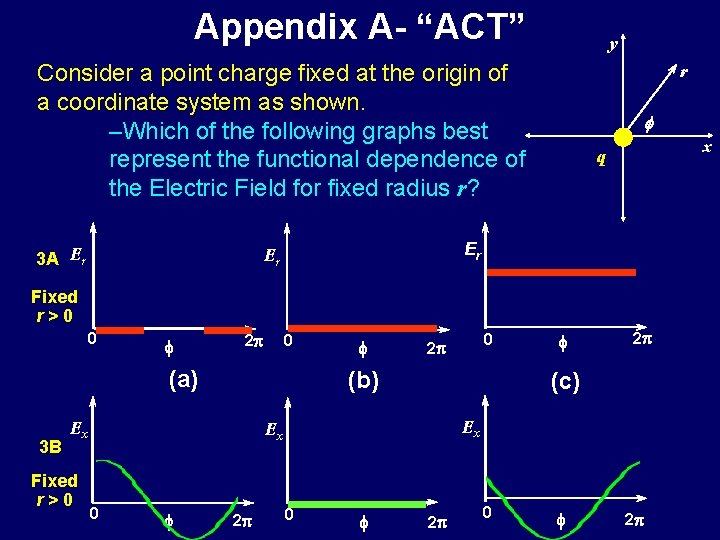
Appendix A- “ACT” y Consider a point charge fixed at the origin of a coordinate system as shown. –Which of the following graphs best represent the functional dependence of the Electric Field for fixed radius r? 3 A Er r f x q Er Er Fixed r>0 0 f 2 p 0 (a) 3 B f 2 p (c) Ex Ex 0 0 2 p (b) Ex Fixed r>0 f 2 p

Appendix A “ACT” y Consider a point charge fixed at the origin of a coordinate system as shown. – Which of the following graphs best represent the functional dependence of the Electric Field for fixed radius r? 3 A Er r f x q Er Er Fixed r>0 0 f (a) 2 p 0 f (b) 2 p 0 f 2 p (c) • At fixed r, the radial component of the field is a constant, independent of f!! • For r>0, this constant is > 0. (note: the azimuthal component Ef is, however, zero)
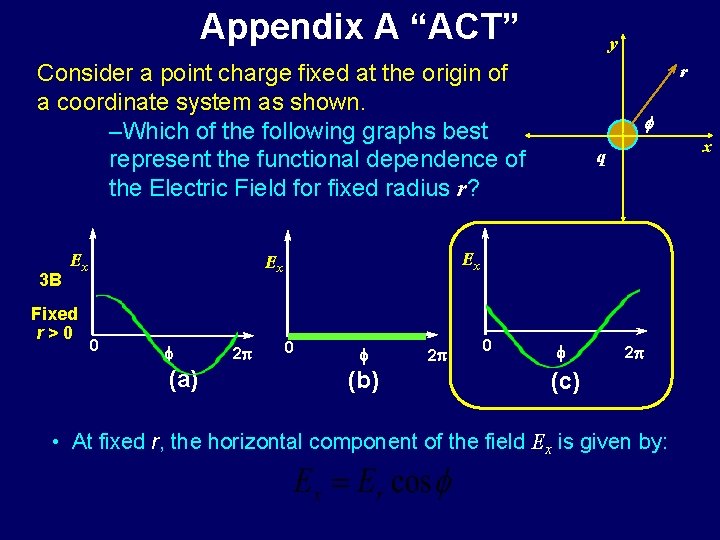
Appendix A “ACT” y Consider a point charge fixed at the origin of a coordinate system as shown. –Which of the following graphs best represent the functional dependence of the Electric Field for fixed radius r? 3 B Ex Fixed r>0 f (a) 2 p f x q Ex Ex 0 r 0 f (b) 2 p 0 f 2 p (c) • At fixed r, the horizontal component of the field Ex is given by:

y Appendix B: Electric Dipole +q a -q r E x E What is the E-field generated by this arrangement of charges? Calculate for a point along x-axis: (x, 0) Ex = ? ? Symmetry Ex(x, 0) = 0 Ey = ? ?
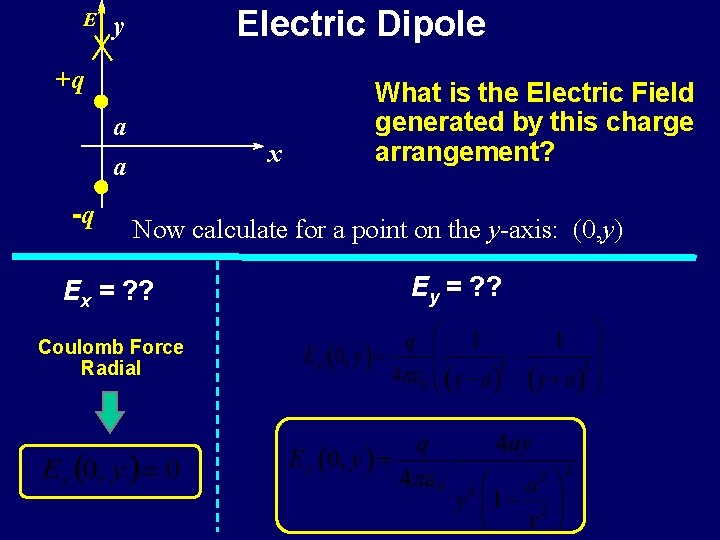
E Electric Dipole y +q a x a -q What is the Electric Field generated by this charge arrangement? Now calculate for a point on the y-axis: (0, y) Ex = ? ? Coulomb Force Radial Ey = ? ?
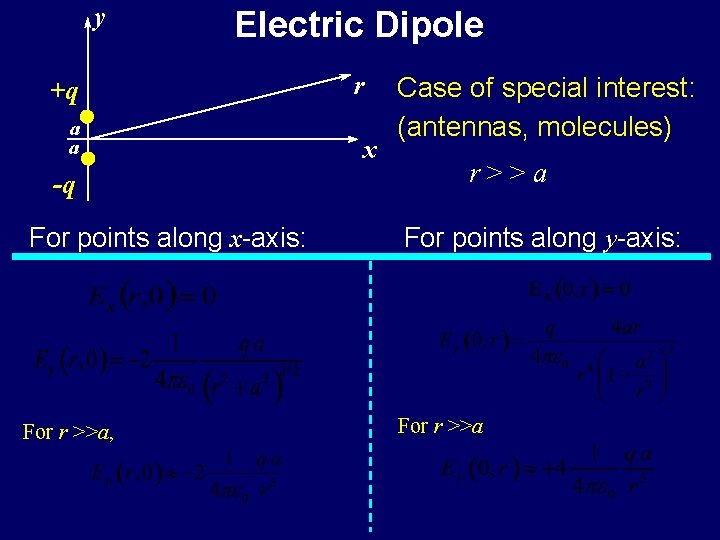
y Electric Dipole +q a a -q r x Case of special interest: (antennas, molecules) r>>a For points along x-axis: For points along y-axis: For r >>a, For r >>a
- Slides: 37