Last Chapter Graphs Paths Circuits Euler Discrete Math

Last Chapter � Graphs � Paths � Circuits � Euler

Discrete Math Traveling Salesman Problems

Lecture Circuit � You are invited to go on a lecture circuit to colleges across the country. � The company said they will cover for a part of your travel expense and you will have to cover the rest. � The cities you are able to visit are…

Pick 5 of the cities below � � � � � � Seattle Portland Spokane Boise Salt Lake City Reno Sacramento San Francisco San Jose Las Vegas Los Angeles San Diego Phoenix Charleston Tampa Orlando Ft. Lauderdale Raleigh Richmond Washington DC Philadelphia New York Providence Boston � � � � � � Denver Albuquerque San Antonio Austin Houston Dallas Oklahoma City Kansas City Little Rock New Orleans Jackson Memphis St. Louis Pensacola Atlanta Nashville Chicago Indianapolis Minneapolis/St. Paul Detroit Cleveland Pittsburgh Charlotte

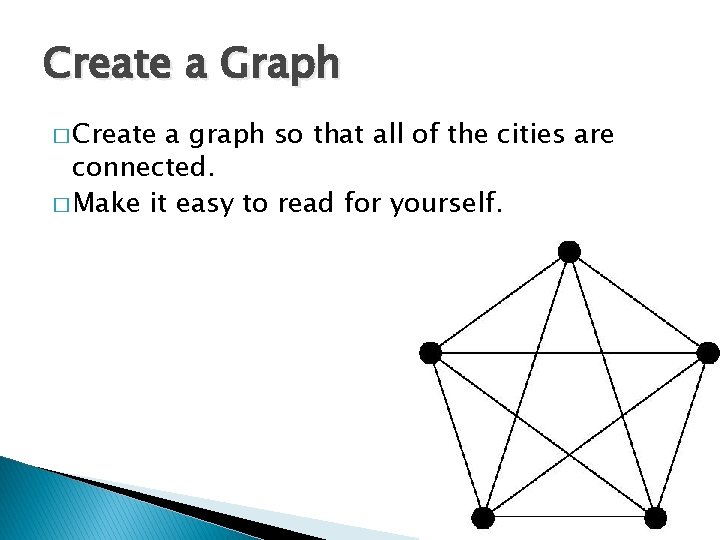
Create a Graph � Create a graph so that all of the cities are connected. � Make it easy to read for yourself.

Go to Southwest Airlines � Find � You the cost for your flights. should have 10 flights to look up. � Write the cost on each edge.

� How many different circuits do you make? � Which � What � How circuit would you use? was its cost? did you find this circuit? What was your process for choosing flights?

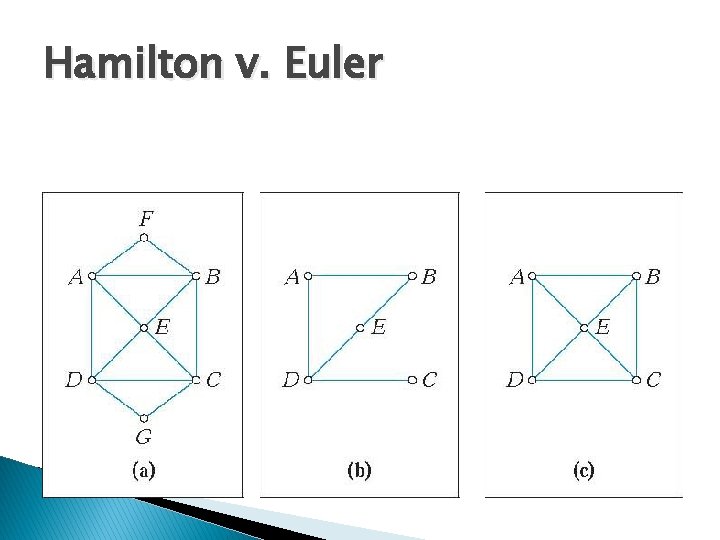
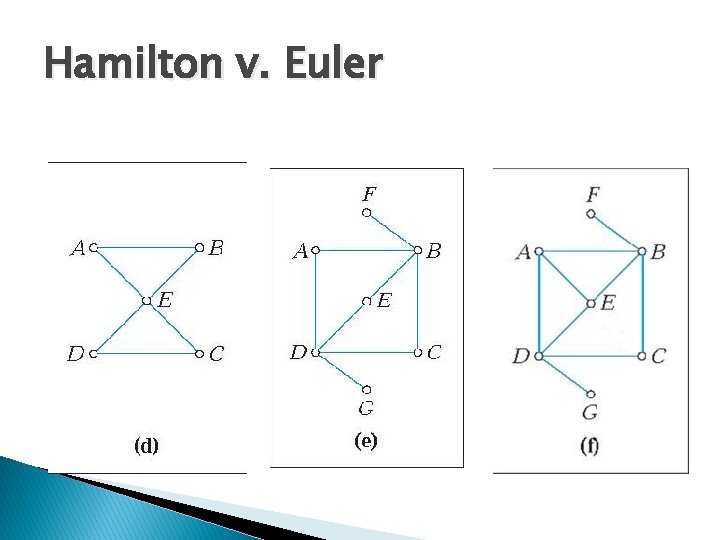
Hamilton Paths and Circuits � Hamilton Path- A path that crosses ever VERTEX once and only once � Hamilton Circuit- A Circuit that crosses ever VERTEX once and ends in the place it started.

Hamilton v. Euler

Hamilton v. Euler

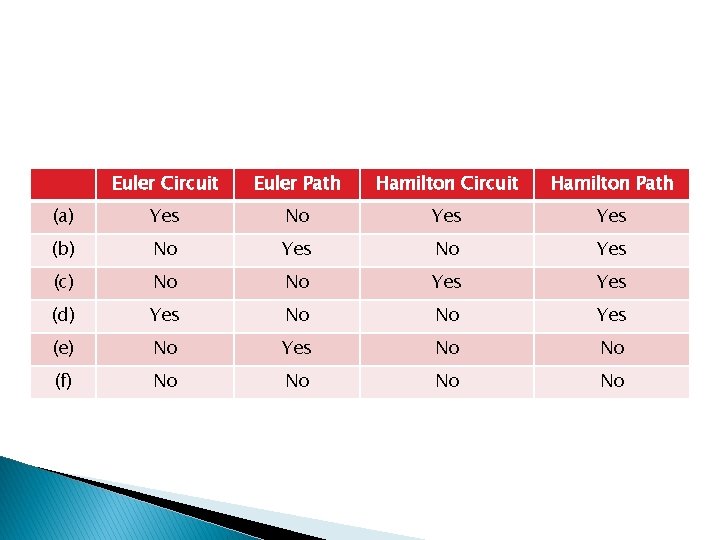
Euler Circuit Euler Path Hamilton Circuit Hamilton Path (a) Yes No Yes (b) No Yes (c) No No Yes (d) Yes No No Yes (e) No Yes No No (f) No No

What we learn from this table � If there is a Hamilton Circuit, then there is a Hamilton Path (Drop the last edge that creates the circuit). � There is no connection between Euler and Hamilton � There is no easy theorem to see if there is a Hamilton Circuit or Path.

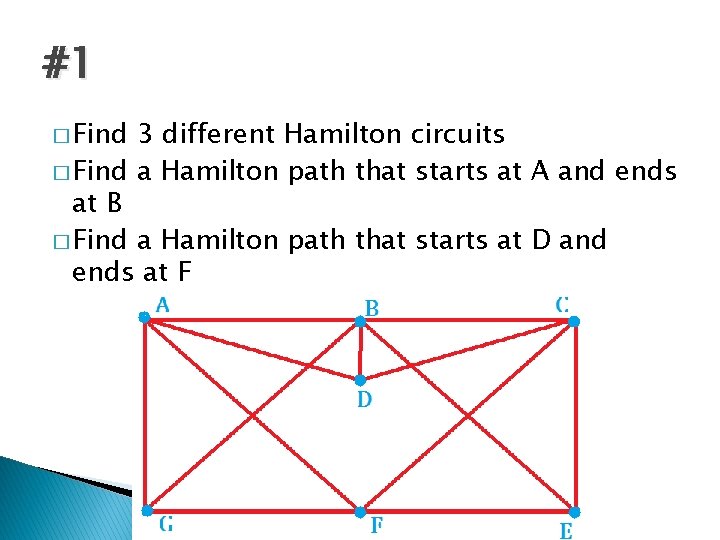
#1 � Find 3 different Hamilton circuits � Find a Hamilton path that starts at A and ends at B � Find a Hamilton path that starts at D and ends at F

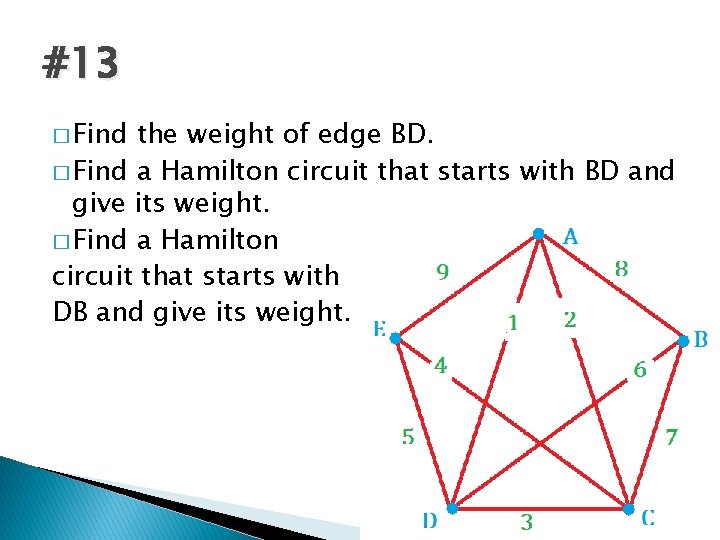
#13 � Find the weight of edge BD. � Find a Hamilton circuit that starts with BD and give its weight. � Find a Hamilton circuit that starts with DB and give its weight.

Problems Page 226 #2, 5, 6, 9, 10, 14, 15, and 16

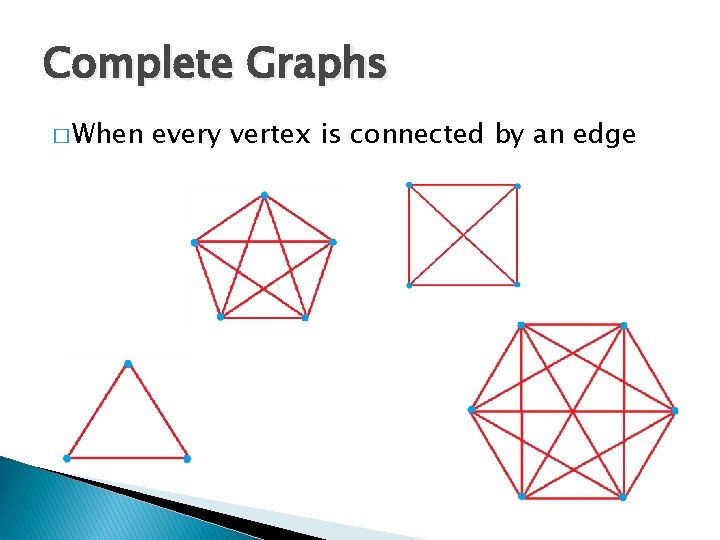
Complete Graphs � When every vertex is connected by an edge

Complete Graph �

How many edges �

How many paths �

#21 (a) 20!

Problems Page 229 #17 -28

TSP vocab � Sites: The vertices on the graph � Costs: � Tour: The weight of the edges A Hamilton Circuit � Optimal Tour: Hamilton Circuit of least weight

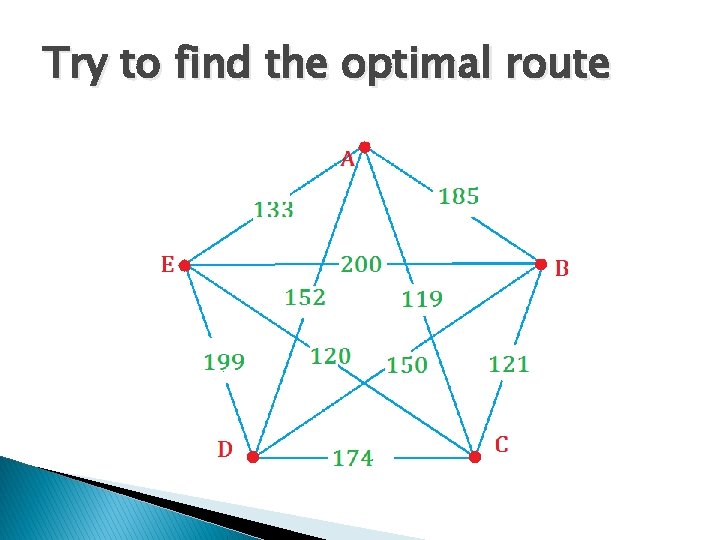
Try to find the optimal route

Simple Strategies � Exhaustive Search: Make a list of all possible routes. The previous example has 24 possible. � Go Cheap: Go to the cheapest city. Continue by going through the cheapest routes possible.

Brute-Force Algorithm 1. 2. 3. Make a list of all possible routes Calculate all the tours Choose the one with the smallest number

Brute-Force � This will ALWAYS get you the optimal tour. � Problem: it is an INEFFICIENT ALGORITHM. This means that it can take way to long to find your solution. ◦ Even with computers

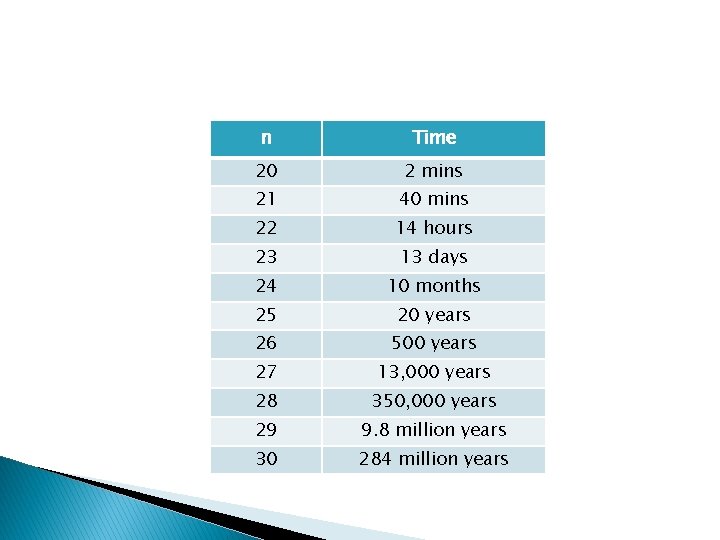
Super Computer �

n Time 20 2 mins 21 40 mins 22 14 hours 23 13 days 24 10 months 25 20 years 26 500 years 27 13, 000 years 28 350, 000 years 29 9. 8 million years 30 284 million years

Nearest-Neighbor � Start at the starting vertex � Go to the “nearest neighbor” (edge with the lowest amount) � Continue through all the points � End at your starting vertex

Nearest-Neighbor � This is not optimal because it might not give us our optimal route � But this is effective because it is proportional to the size of the graph ◦ 10 vertices= 10 steps ◦ 30 vertices= 30 steps

Approximate Algorithms � Using Algorithms to get close to the optimal but might not be the optimal. � Ask yourself: Is a 12. 49% relative error good or would we have to be closer?

Repetitive Nearest-Neighbor � Just like Nearest-Neighbor, but you create a circuit for all the vertices to be your starting point.

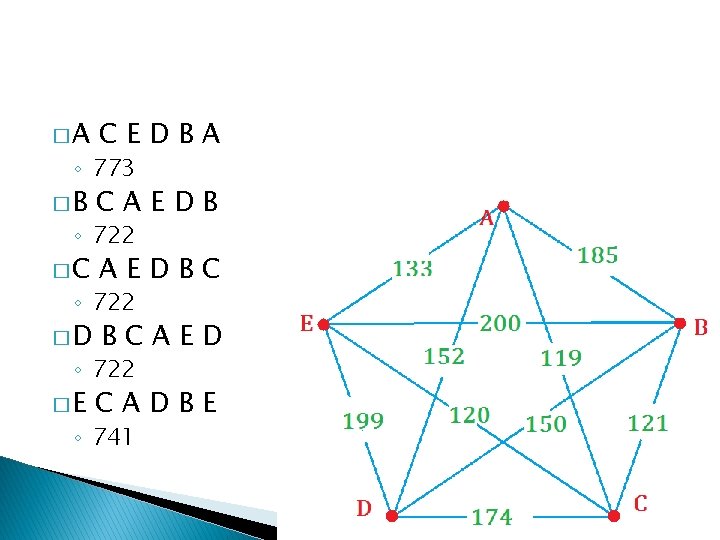
�A CEDBA �B CAEDB �C AEDBC �D BCAED �E CADBE ◦ 773 ◦ 722 ◦ 741

Cheapest Link � Find the cheapest edge and mark it � Pick the next smallest edge � Keep picking the smallest edges ◦ Do not close the circuit ◦ Do not have 3 edges go to the same vertex � Close the circuit to finish

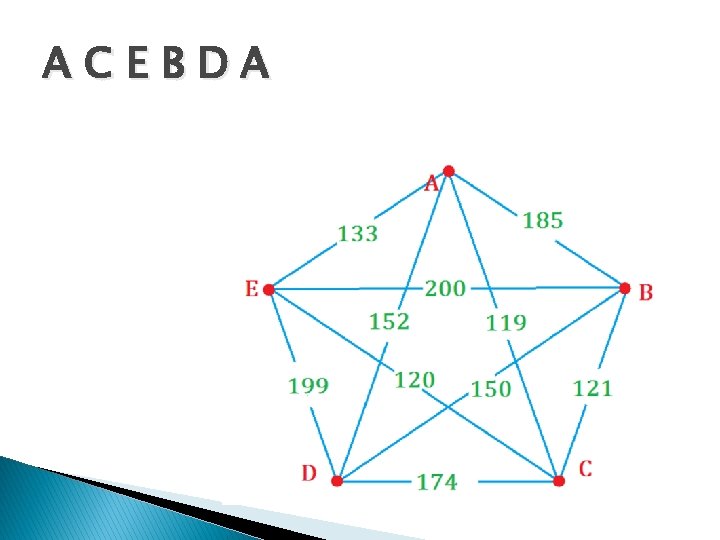
ACEBDA

Problems Chapter 6 #30, 31, 35, 36, 38, 41, 42, 44, 47, 48