Largescale semidefinite programs and applications to polynomial optimization

Large-scale semidefinite programs and applications to polynomial optimization and machine learning Georgina Hall Princeton, ORFE 1

What is a semidefinite program? • Definition: Example: 2

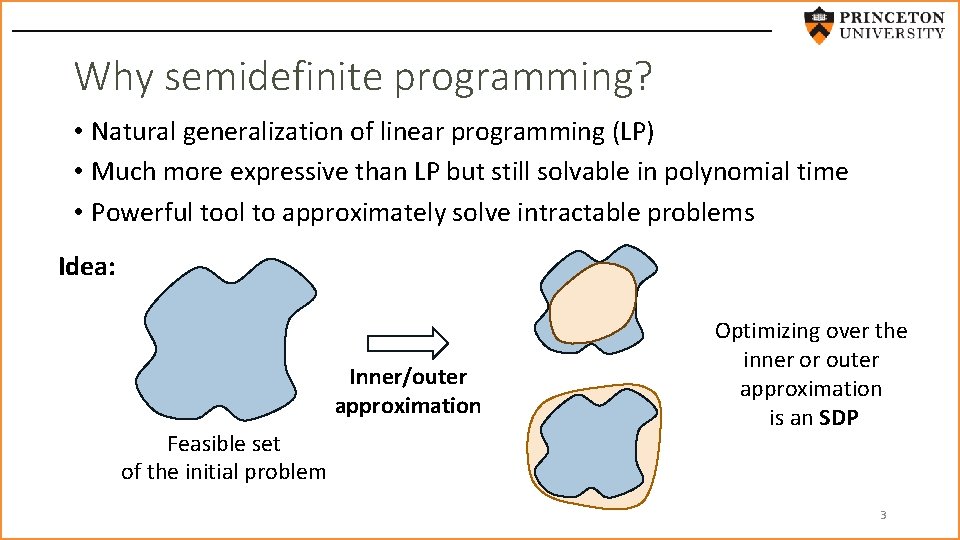
Why semidefinite programming? • Natural generalization of linear programming (LP) • Much more expressive than LP but still solvable in polynomial time • Powerful tool to approximately solve intractable problems Idea: Inner/outer approximation Feasible set of the initial problem Optimizing over the inner or outer approximation is an SDP 3

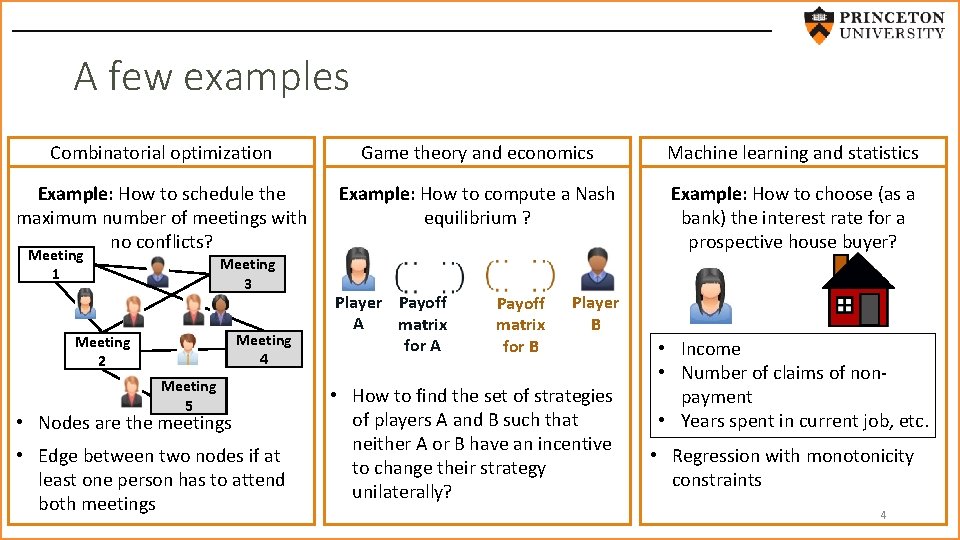
A few examples Combinatorial optimization Game theory and economics Machine learning and statistics Example: How to schedule the maximum number of meetings with no conflicts? Example: How to compute a Nash equilibrium ? Example: How to choose (as a bank) the interest rate for a prospective house buyer? Meeting 1 Meeting 3 Meeting 4 Meeting 2 Meeting 5 • Nodes are the meetings • Edge between two nodes if at least one person has to attend both meetings Player Payoff A matrix for A Payoff matrix for B Player B • How to find the set of strategies of players A and B such that neither A or B have an incentive to change their strategy unilaterally? • Income • Number of claims of nonpayment • Years spent in current job, etc. • Regression with monotonicity constraints 4

A specific example in random networks (1/2) Example: How to recognize a fake news website from a legitimate news website? How to classify each website as legitimate vs fake from the graph only? Idea: members of the same community are more likely to be connected. 5

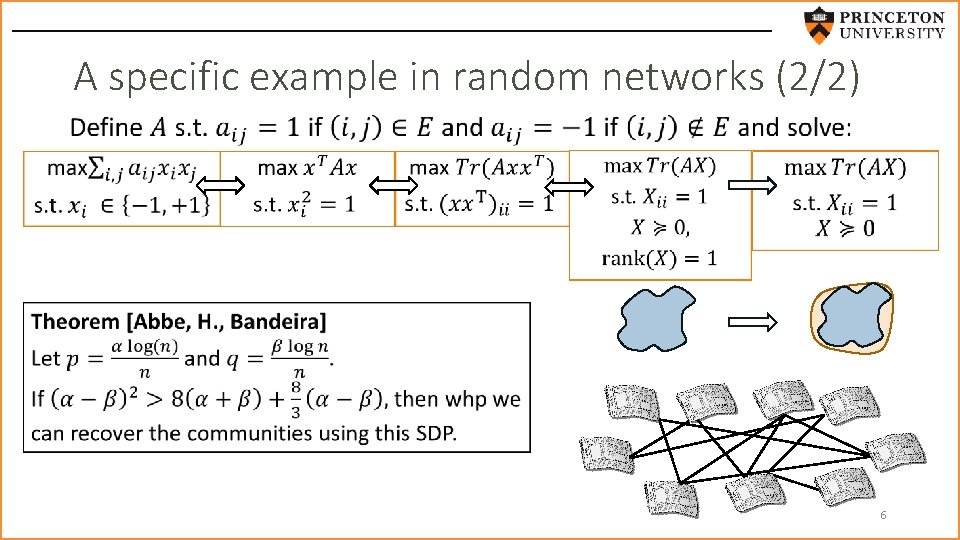
A specific example in random networks (2/2) 6

My work in a nutshell (1/2) Designing SDP-based approximations for intractable problems, and solving SDPs faster. Semidefinite programming Efficiently solving optimization problems over nonnegative polynomials. (fundamental problem in computational algebra) Problem: Example: Applications: POPs, control, ML, etc. Opt. over nonnegative polynomials 7

My work in a nutshell (2/2) Large-scale semidefinite programs Theory of nonnegative polynomials Applications of optimizing over nonnegative polynomials Application of semidefinite programming This talk: Part I: Large-scale SDPs Part II. a: Monotone regression Part II. b: Difference of convex programming 8

Part I Large-scale semidefinite programs 9

Reminder: semidefinite programming • Faster ways of solving large-scale SDPs? 10

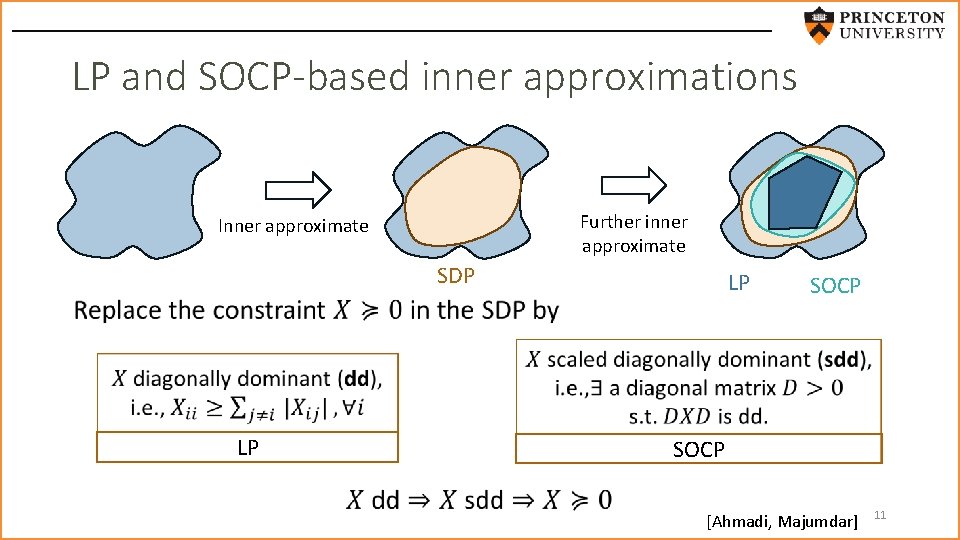
LP and SOCP-based inner approximations Further inner approximate Inner approximate SDP LP • SOCP LP SOCP [Ahmadi, Majumdar] 11

LP and SOCP-based inner approximations Hard problem Semidefinite program Linear or second order cone program How to bridge this gap? Idea: Iteratively construct a sequence of improving LP/SOCP-based inner approximations Initialization: Start with dd or sdd Method 1: Basis Pursuit Method 2: Column Generation [Ahmadi, H. ] [Ahmadi, Dash, H. ] 12

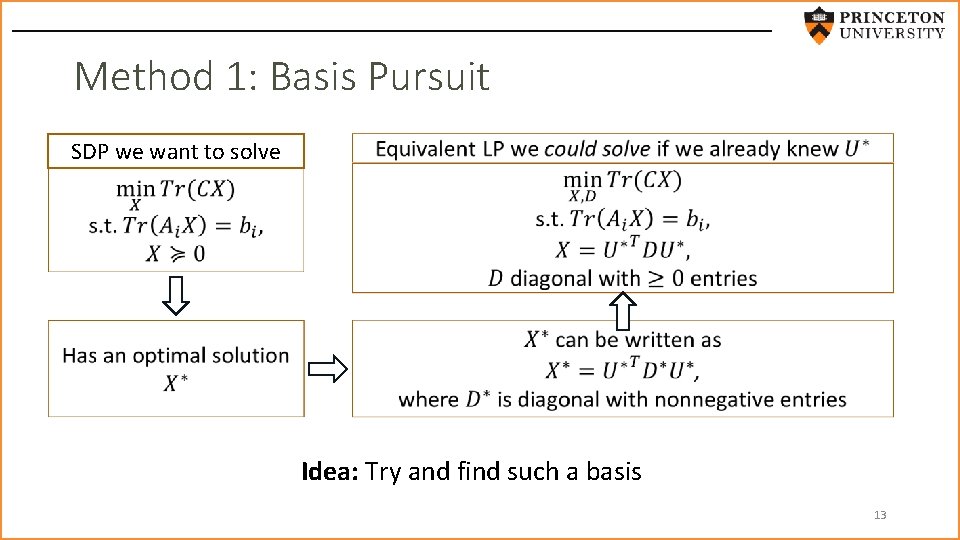
Method 1: Basis Pursuit SDP we want to solve Idea: Try and find such a basis 13

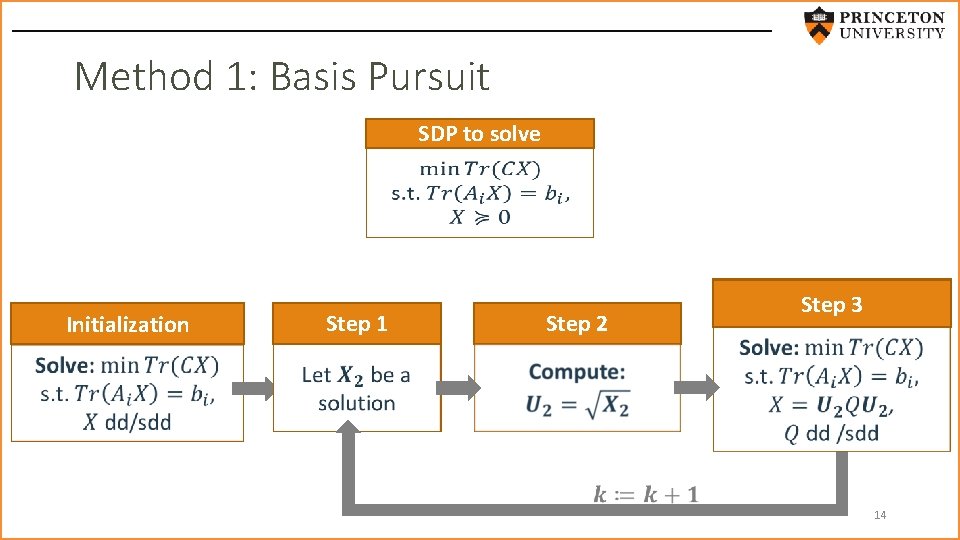
Method 1: Basis Pursuit SDP to solve Step 1 Initialization Step 2 Step 3 14

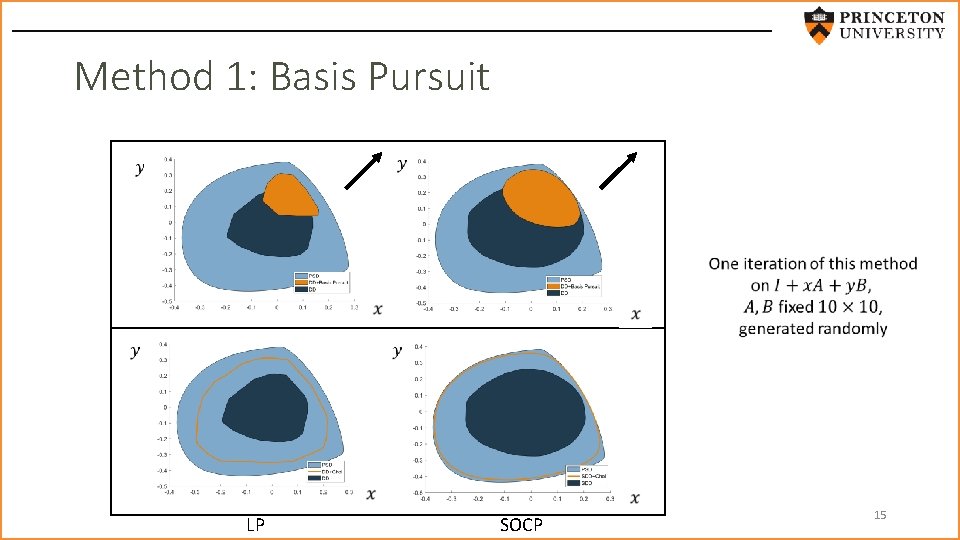
Method 1: Basis Pursuit LP SOCP 15

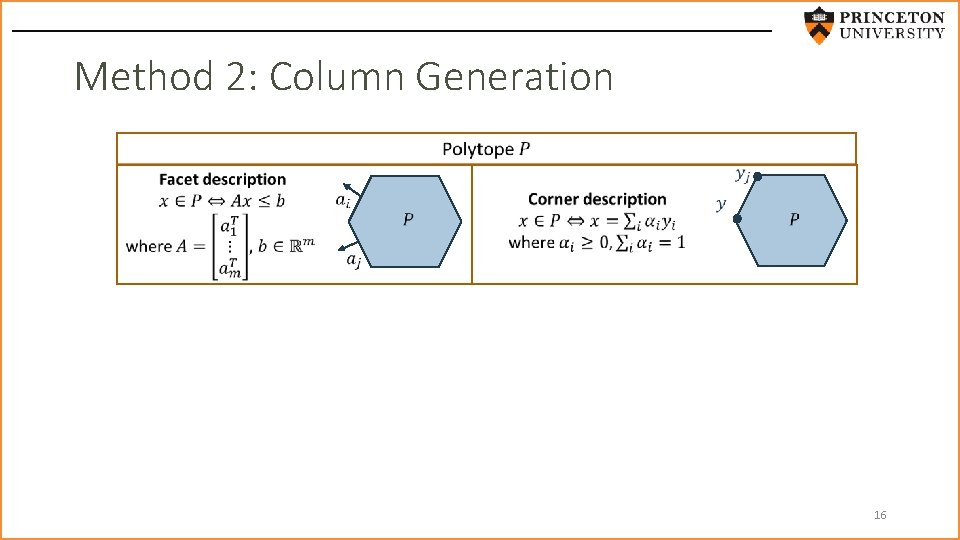
Method 2: Column Generation DD cone SDD cone Facet description Extreme ray description + + + 16

Method 2: Column Generation • Initial SDP Find a new “atom” Take the dual 17

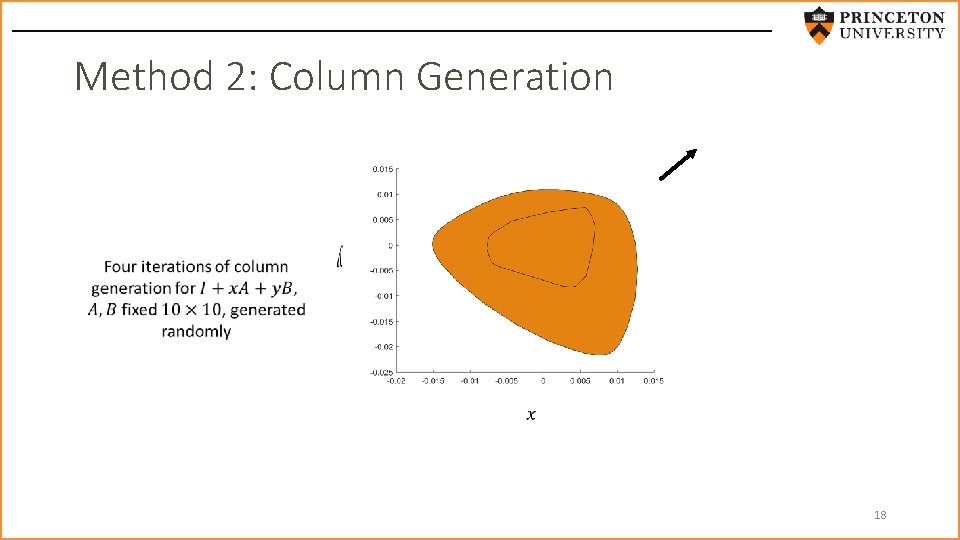
Method 2: Column Generation 18

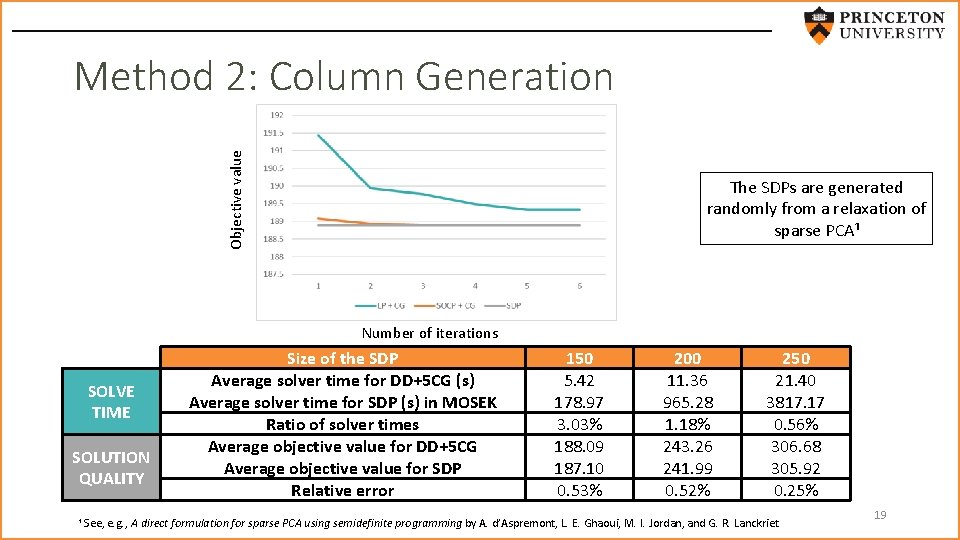
Objective value Method 2: Column Generation The SDPs are generated randomly from a relaxation of sparse PCA¹ Number of iterations SOLVE TIME SOLUTION QUALITY Size of the SDP Average solver time for DD+5 CG (s) Average solver time for SDP (s) in MOSEK Ratio of solver times Average objective value for DD+5 CG Average objective value for SDP Relative error 150 5. 42 178. 97 3. 03% 188. 09 187. 10 0. 53% 200 11. 36 965. 28 1. 18% 243. 26 241. 99 0. 52% 250 21. 40 3817. 17 0. 56% 306. 68 305. 92 0. 25% ¹ See, e. g. , A direct formulation for sparse PCA using semidefinite programming by A. d’Aspremont, L. E. Ghaoui, M. I. Jordan, and G. R. Lanckriet 19

Part II. a Application of optimizing over nonnegative polynomials: Monotone regression [Ahmadi, Curmei, H. ] 20

Optimizing over nonnegative polynomials Intractable constraint How to optimize over this set? First, how to test membership to this set? 21

Nonnegative and sum of squares polynomials (1/2) • 22

Nonnegative and sum of squares polynomials (2/2) Optimizing over nonnegative polynomials Inner approx. Semidefinite program 22

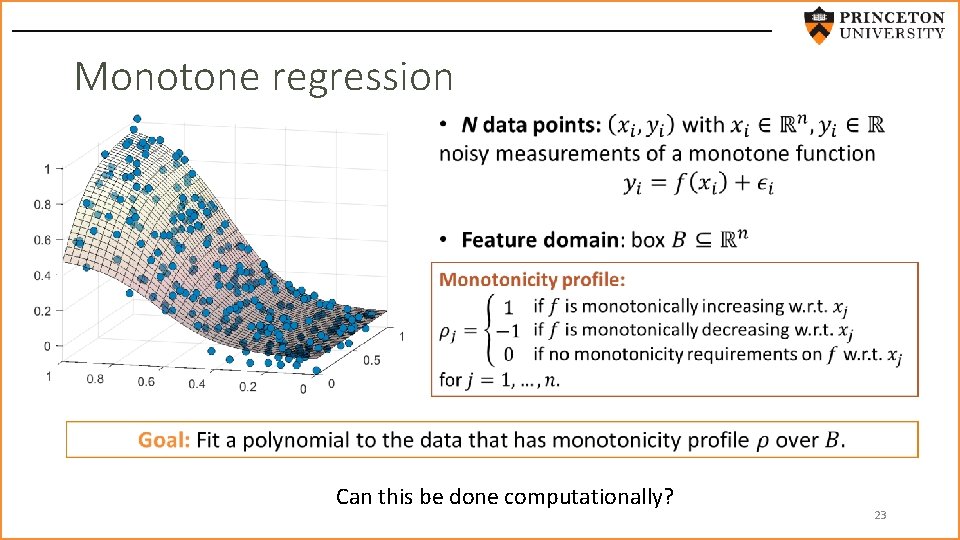
Monotone regression Can this be done computationally? 23

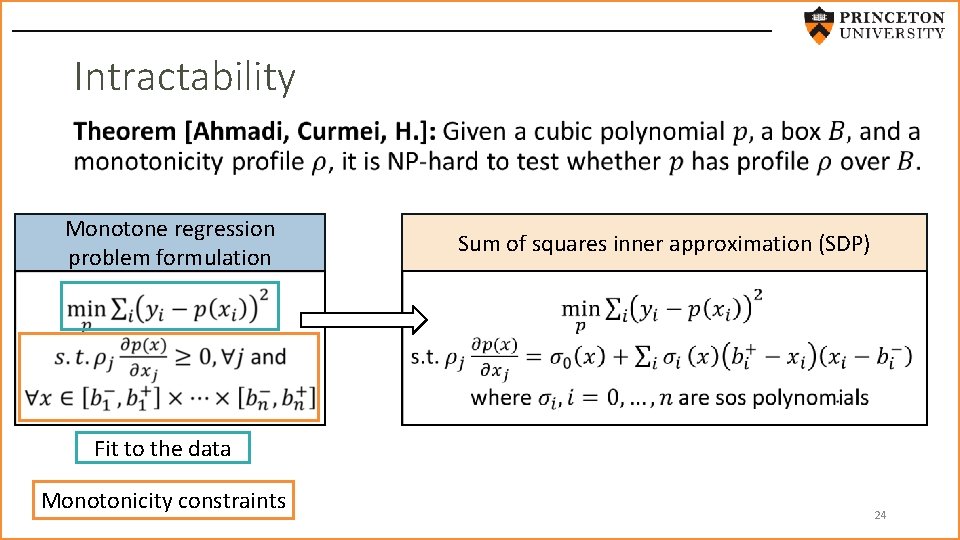
Intractability • Monotone regression problem formulation Sum of squares inner approximation (SDP) Fit to the data Monotonicity constraints 24

Approximation theorem • Proof uses results from approximation theory and Putinar’s Positivstellensatz 25

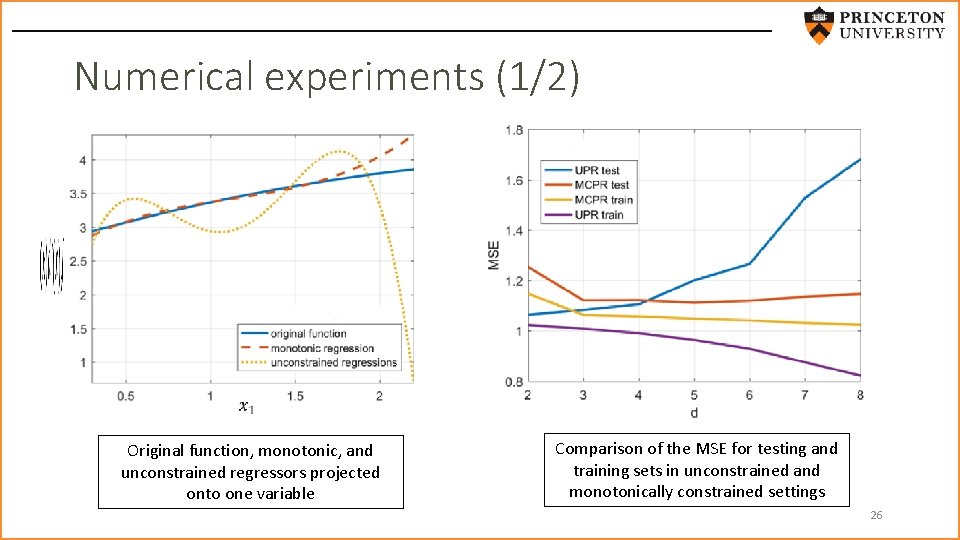
Numerical experiments (1/2) Original function, monotonic, and unconstrained regressors projected onto one variable Comparison of the MSE for testing and training sets in unconstrained and monotonically constrained settings 26

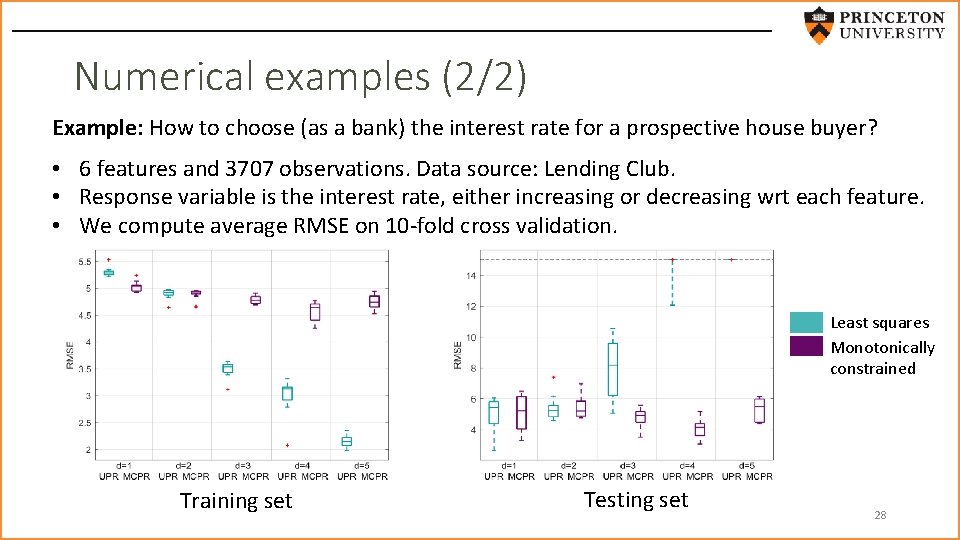
Numerical examples (2/2) Example: How to choose (as a bank) the interest rate for a prospective house buyer? • 6 features and 3707 observations. Data source: Lending Club. • Response variable is the interest rate, either increasing or decreasing wrt each feature. • We compute average RMSE on 10 -fold cross validation. Least squares Monotonically constrained Training set Testing set 28

Part II. b Application of optimizing over nonnegative polynomials: difference of convex programming [Ahmadi, H. ] Winner of the 2016 INFORMS Computing Society Best Student Paper Award 29

Difference of convex programming (1/2) • What if such a decomposition is not given to us? Hiriart-Urruty, 1985 Tuy, 1995 30

Difference of convex decomposition • DC decomposition problem formulation Questions: • Is this problem always feasible? i. e. , can you always write any polynomial as the difference of two convex polynomials? • Can it be solved computationally? • Does it have a unique solution? 31

Convex and sos-convex polynomials Optimizing over convex polynomials Inner approx. Semidefinite program • Note that: sos-convexity 32

Back to an efficient dc decomposition DC decomposition problem formulation Semidefinite program Inner approx. Are these problems always feasible? Theorem [Ahmadi, H. ]: Any polynomial can be written as the difference of two sos-convex polynomials (and hence as the difference of two convex polynomials). 33

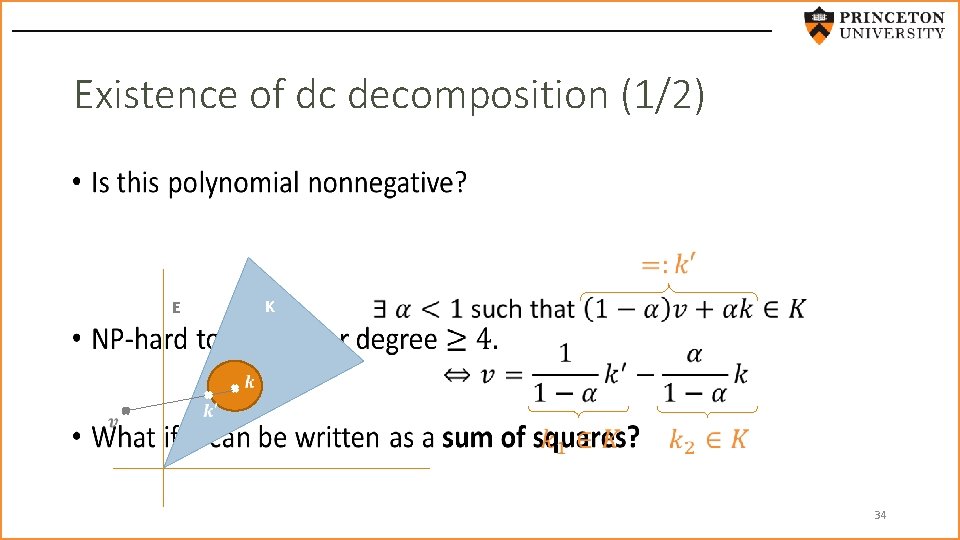
Existence of dc decomposition (1/2) • K E 34

Existence of dc decomposition (2/2) • Questions: • Is this problem always feasible? • Can it be solved computationally? • Is the solution unique? DC decomposition problem formulation Yes No Initial decomposition Alternative decompositions “Best decomposition? ” 35

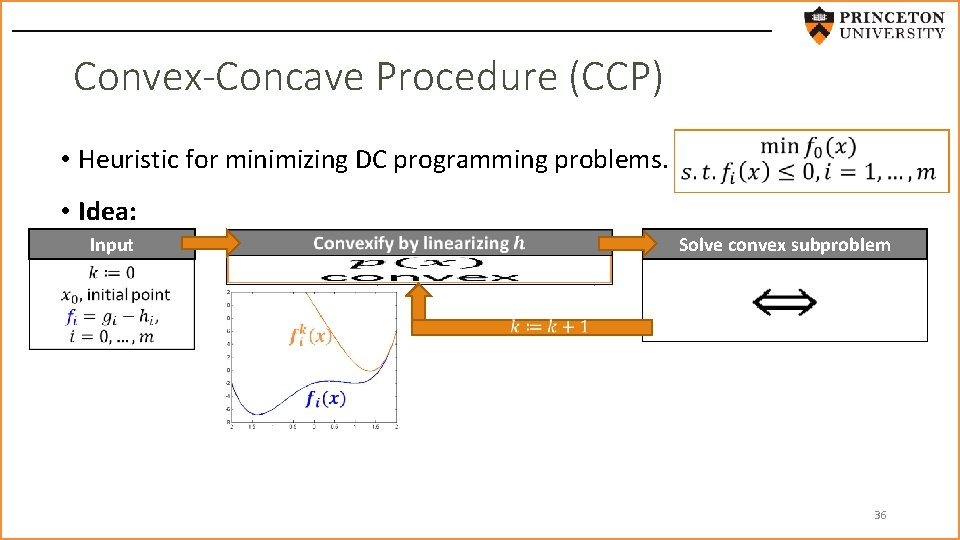
Convex-Concave Procedure (CCP) • Heuristic for minimizing DC programming problems. • Idea: Input Solve convex subproblem convex affine 36

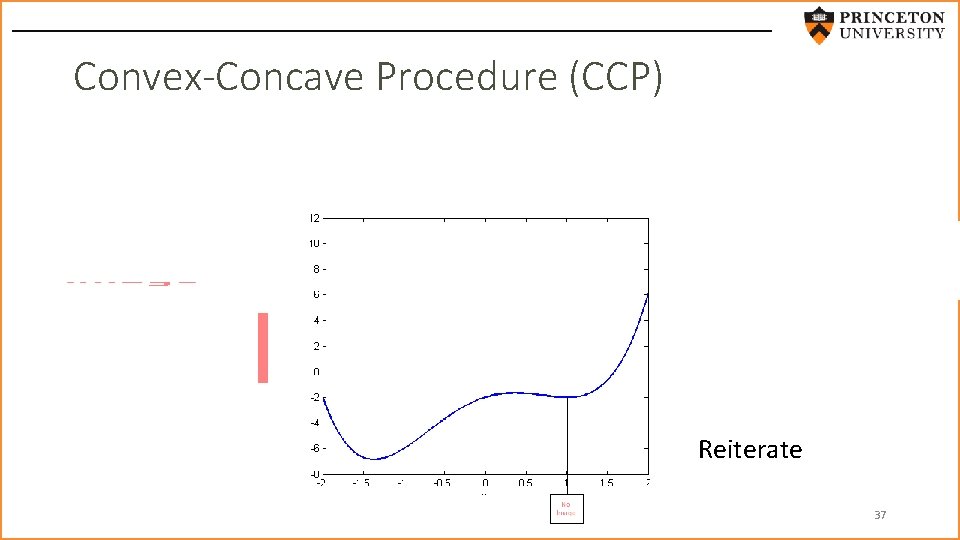
Convex-Concave Procedure (CCP) • Reiterate 37

Picking the “best” decomposition for CCP Algorithm Idea Mathematical translation 38

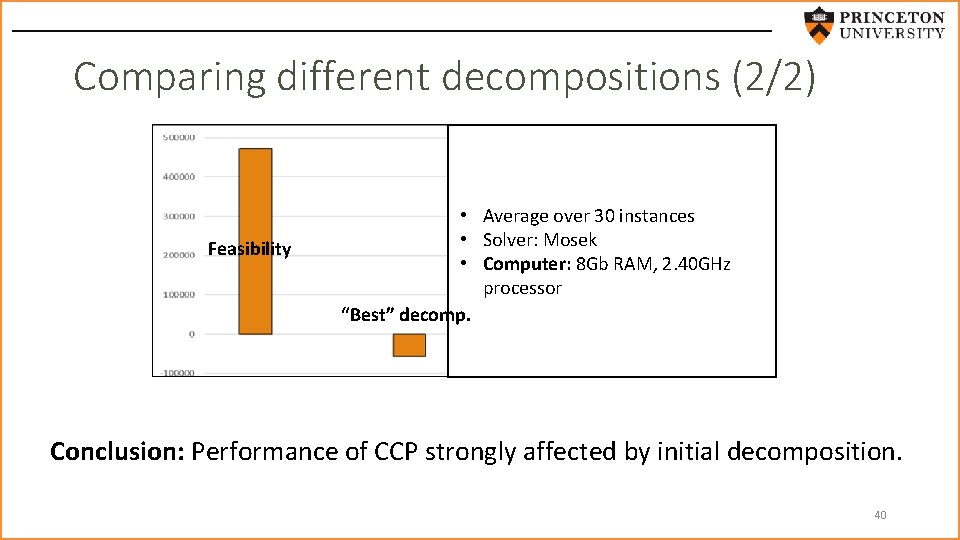
Comparing different decompositions (1/2) • Feasibility “Best” decomposition 39

Comparing different decompositions (2/2) Feasibility • Average over 30 instances • Solver: Mosek • Computer: 8 Gb RAM, 2. 40 GHz processor “Best” decomp. Conclusion: Performance of CCP strongly affected by initial decomposition. 40

Main messages (1/2) • Semidefinite programming (SDP) can provide very powerful bounds for many intractable problems. or Meeting 1 Meeting 2 Meeting 3 Meeting 4 • Large-scale SDPs are expensive to solve. • We proposed two methods to solve large-scale SDPs that are based on generating adaptive sequences of LPs and SOCPs. Method 1: Basis Pursuit Method 2: Column Generation 41

Main messages (2/2) • Optimizing over nonnegative polynomials has many applications. Focused on monotone regression and difference of convex programming. • Gave an SDP machinery for optimizing over monotone polynomials with approximation results. • Showed that any polynomial can be decomposed into the difference of two convex polynomials and that the decomposition impacts the performance of CCP. 42

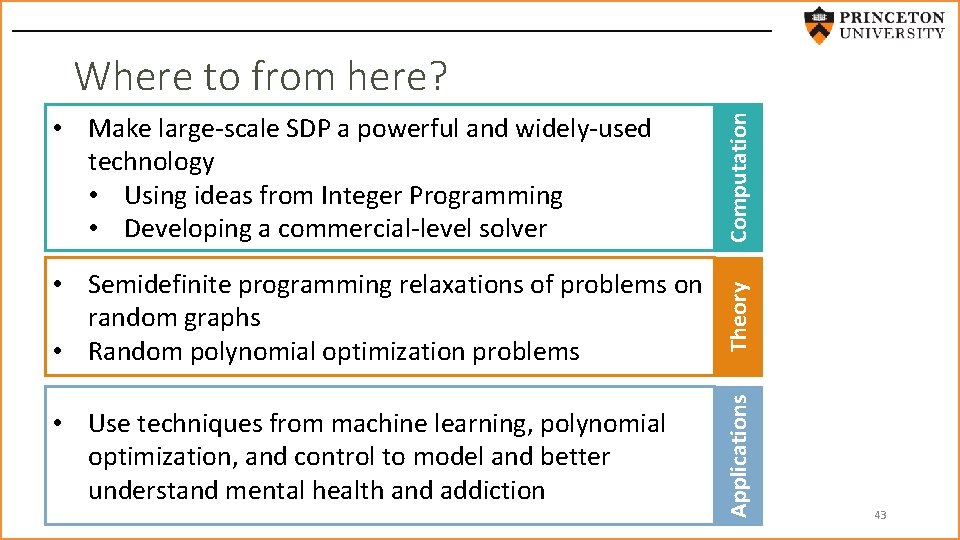
• Semidefinite programming relaxations of problems on random graphs • Random polynomial optimization problems Theory • Use techniques from machine learning, polynomial optimization, and control to model and better understand mental health and addiction Applications • Make large-scale SDP a powerful and widely-used technology • Using ideas from Integer Programming • Developing a commercial-level solver Computation Where to from here? 43

Thank you for listening Questions? Want to know more? http: //scholar. princeton. edu/ghall/ 44

Difference of convex programming (1/2) • Regression Sparsity Convex Concave 45

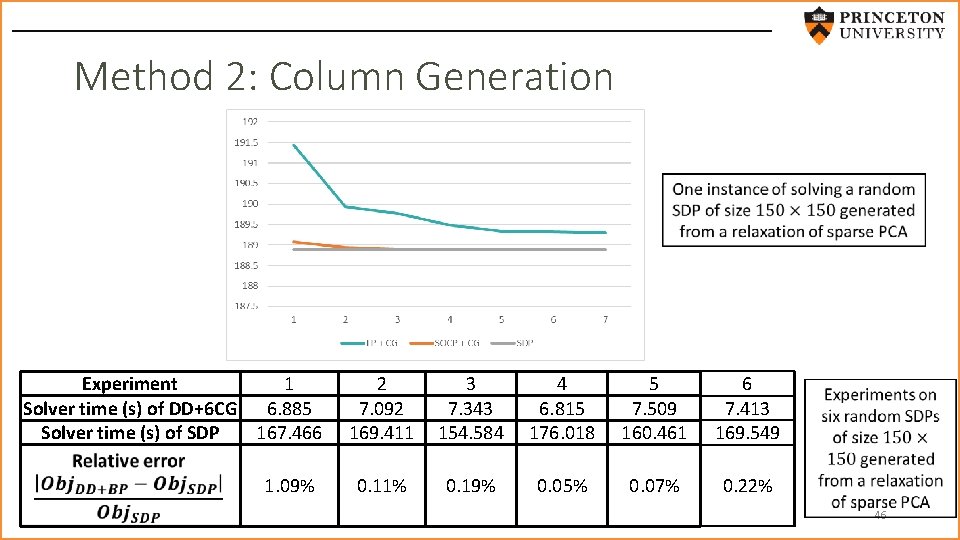
Method 2: Column Generation Experiment 1 Solver time (s) of DD+6 CG 6. 885 Solver time (s) of SDP 167. 466 1. 09% 2 7. 092 169. 411 3 7. 343 154. 584 4 6. 815 176. 018 5 7. 509 160. 461 6 7. 413 169. 549 0. 11% 0. 19% 0. 05% 0. 07% 0. 22% 46