Large Scale Structure of the Universe Evolution of

Large Scale Structure of the Universe

Evolution of the LSS – a brief history Somewhat after recombination -density perturbations are small on nearly all spatial scales. Dark Ages, prior to z=10 -density perturbations in dark matter and baryons grow; on smaller scales perturbations have gone non-linear, d>>1; small (low mass) dark matter halos form; massive stars form in their potential wells and reionize the Universe. z=2 -Most galaxies have formed; they are bright with stars; this is also the epoch of highest quasar activity; galaxy clusters are forming. In LCDM growth of structure on large (linear) scales has nearly stopped, but smaller non-linear scales continue to evolve. z=0 -Small galaxies continue to get merged to form larger ones; in an open and lambda universes large scale (>10 -100 Mpc) potential wells/hill are decaying, giving rise to late ISW. Picture credit: A. Kravtsov, http: //cosmicweb. uchicago. edu/filaments. html

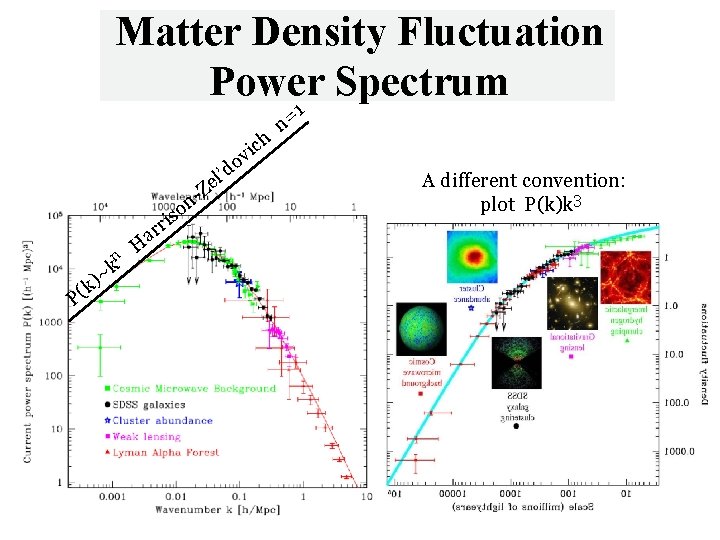
Matter Density Fluctuation Power Spectrum o ch i v n -Z n k P( ~ k) H ar o ris d el’ 1 = n A different convention: plot P(k)k 3

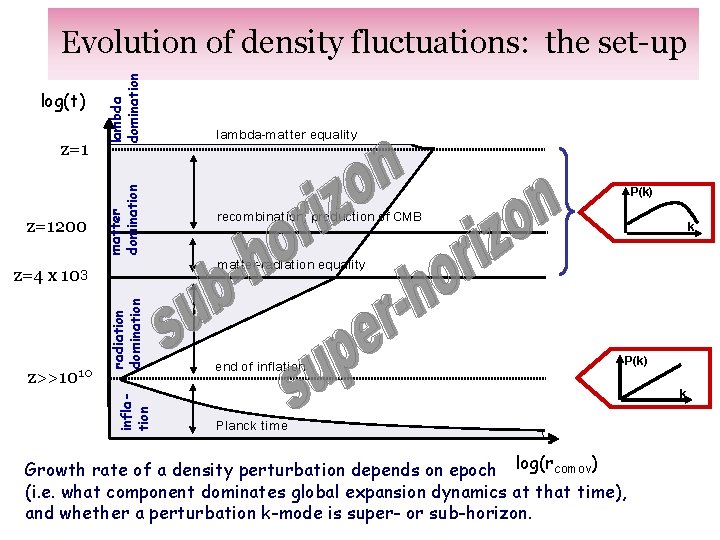
z=1 z=1200 matter domination log(t) lambda domination Evolution of density fluctuations: the set-up P(k) recombination; production of CMB k matter-radiation equality inflation radiation domination z=4 x 103 z>>1010 lambda-matter equality end of inflation P(k) k Planck time Growth rate of a density perturbation depends on epoch log(rcomov) (i. e. what component dominates global expansion dynamics at that time), and whether a perturbation k-mode is super- or sub-horizon.

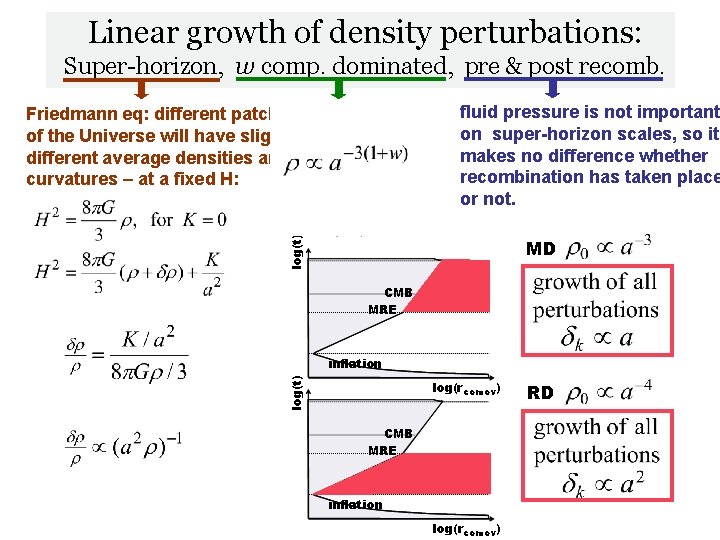
Linear growth of density perturbations: Super-horizon, w comp. dominated, pre & post recomb. fluid pressure is not important on super-horizon scales, so it makes no difference whether recombination has taken place or not. log(t) Friedmann eq: different patches of the Universe will have slightly different average densities and curvatures – at a fixed H: MD CMB MRE log(t) inflation log(rcomov) CMB MRE inflation log(rcomov) RD

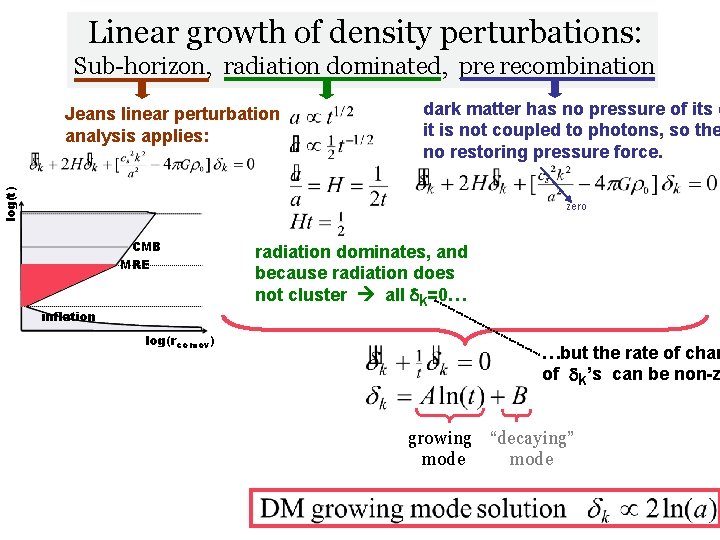
Linear growth of density perturbations: Sub-horizon, radiation dominated, pre recombination dark matter has no pressure of its o it is not coupled to photons, so the no restoring pressure force. log(t) Jeans linear perturbation analysis applies: zero CMB MRE inflation log(rcomov) radiation dominates, and because radiation does not cluster all dk=0… …but the rate of chan of dk’s can be non-z growing “decaying” mode

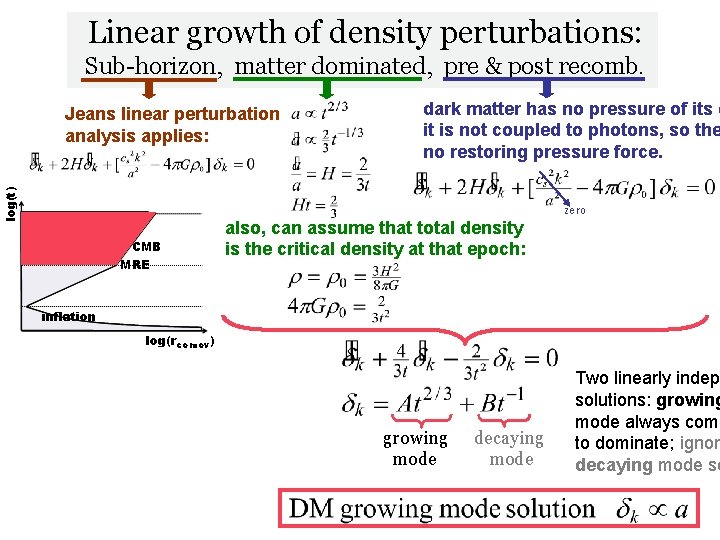
Linear growth of density perturbations: Sub-horizon, matter dominated, pre & post recomb. log(t) Jeans linear perturbation analysis applies: dark matter has no pressure of its o it is not coupled to photons, so the no restoring pressure force. zero CMB MRE also, can assume that total density is the critical density at that epoch: inflation log(rcomov) growing mode decaying mode Two linearly indep solutions: growing mode always come to dominate; ignore decaying mode so

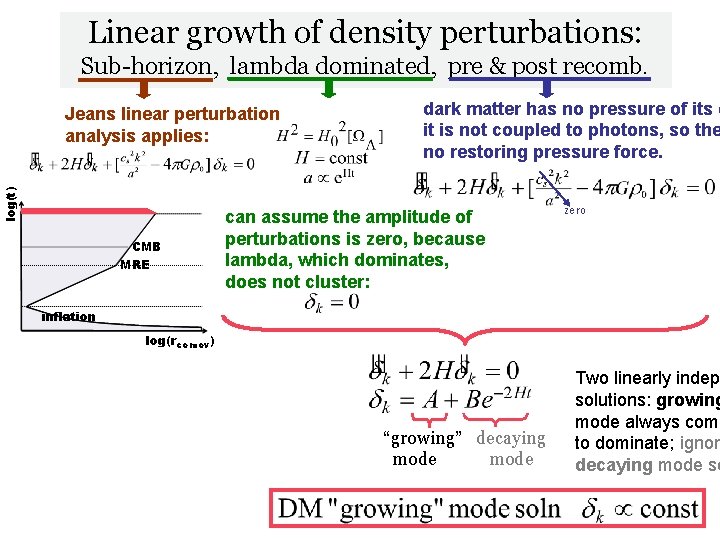
Linear growth of density perturbations: Sub-horizon, lambda dominated, pre & post recomb. log(t) Jeans linear perturbation analysis applies: CMB MRE dark matter has no pressure of its o it is not coupled to photons, so the no restoring pressure force. can assume the amplitude of perturbations is zero, because lambda, which dominates, does not cluster: zero inflation log(rcomov) “growing” decaying mode Two linearly indep solutions: growing mode always come to dominate; ignore decaying mode so

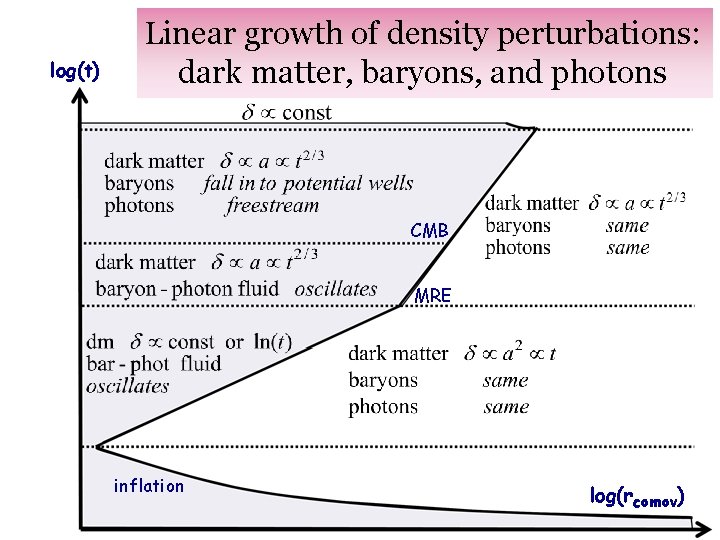
log(t) Linear growth of density perturbations: dark matter, baryons, and photons CMB MRE inflation log(rcomov)

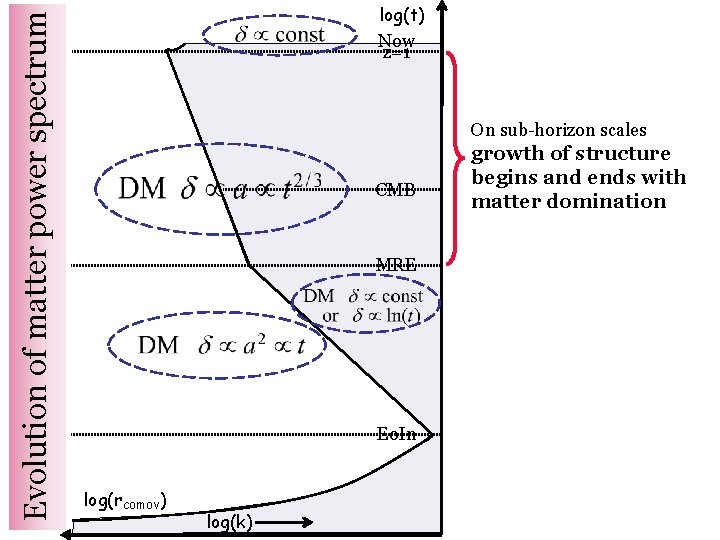
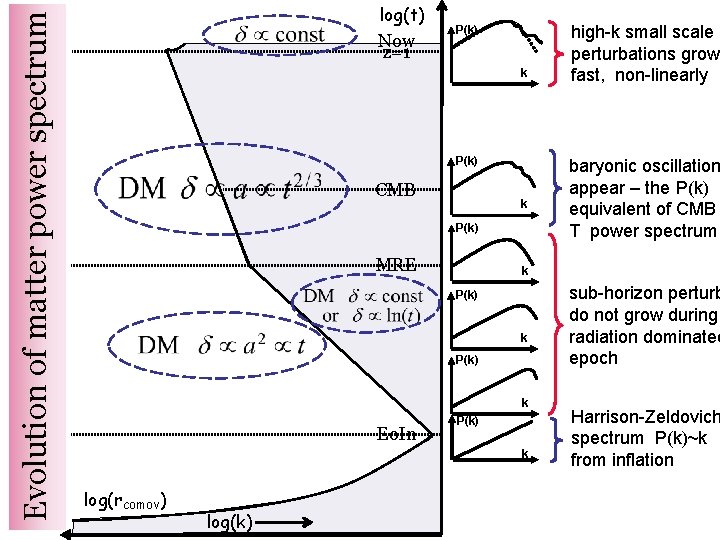
Evolution of matter power spectrum log(t) Now z=1 On sub-horizon scales CMB MRE Eo. In log(rcomov) log(k) growth of structure begins and ends with matter domination

Evolution of matter power spectrum log(t) Now z=1 P(k) k P(k) CMB k P(k) MRE k P(k) k log(rcomov) log(k) baryonic oscillation appear – the P(k) equivalent of CMB T power spectrum k P(k) Eo. In high-k small scale perturbations grow fast, non-linearly sub-horizon perturb do not grow during radiation dominated epoch Harrison-Zeldovich spectrum P(k)~k from inflation

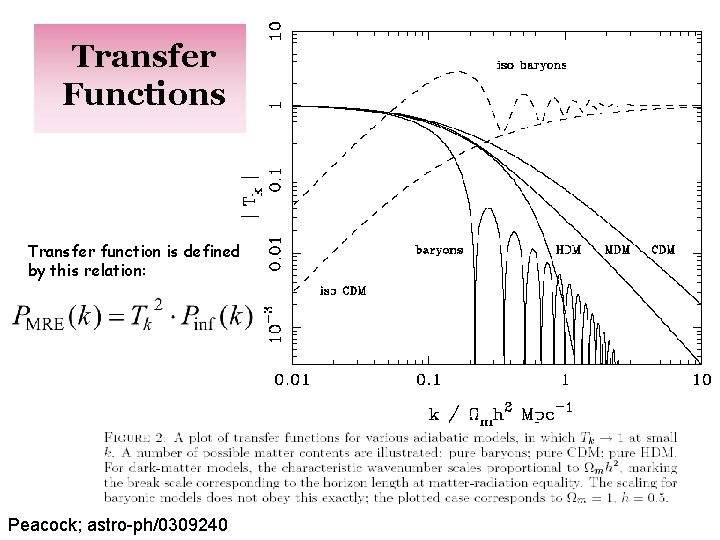
Transfer Functions Transfer function is defined by this relation: Peacock; astro-ph/0309240

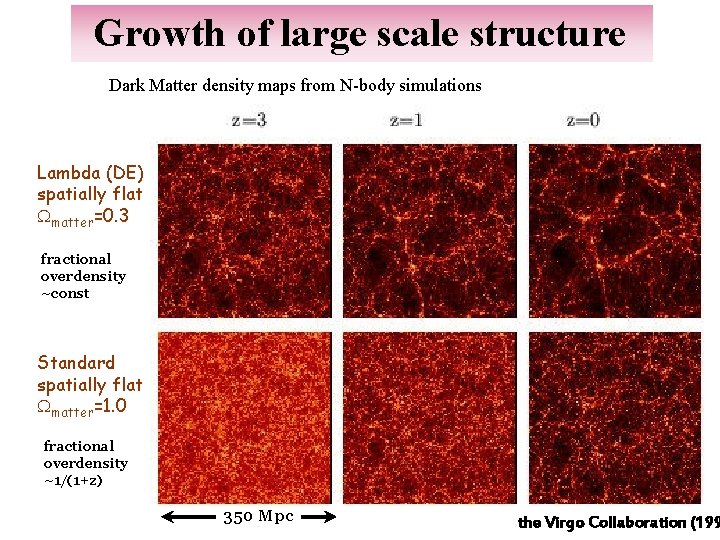
Growth of large scale structure Dark Matter density maps from N-body simulations Lambda (DE) spatially flat Wmatter=0. 3 fractional overdensity ~const Standard spatially flat Wmatter=1. 0 fractional overdensity ~1/(1+z) 350 Mpc the Virgo Collaboration (199

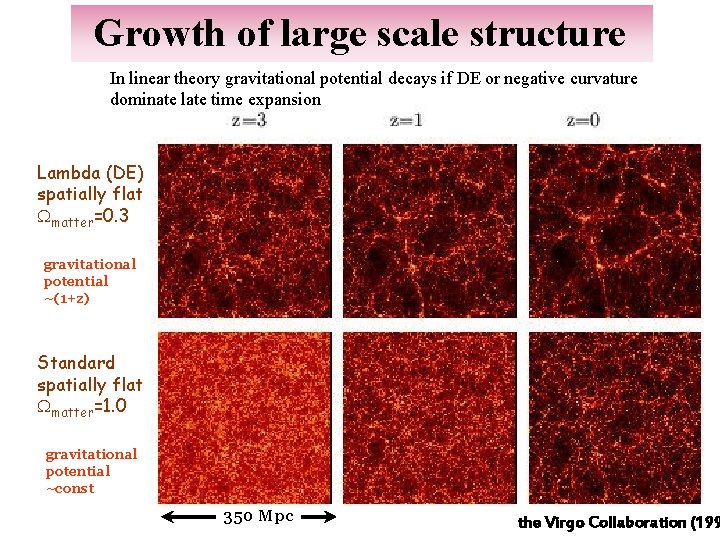
Growth of large scale structure In linear theory gravitational potential decays if DE or negative curvature dominate late time expansion Lambda (DE) spatially flat Wmatter=0. 3 gravitational potential ~(1+z) Standard spatially flat Wmatter=1. 0 gravitational potential ~const 350 Mpc the Virgo Collaboration (199

Late Integrated Sachs-Wolfe (ISW) Effect If a potential well evolves as a photon transverses it, the photon’s energy will change Sachs & Wolfe (1967) Ap. J 147, 73 Crittenden & Turok (1996) PRL 76, 575 photon gains energy after crossing a potential well Energy potential well Look for correlation between CMB temperature fluctuations and nearby structure. Detection of late ISW effect in a flat universe is direct evidence of Dark Energy

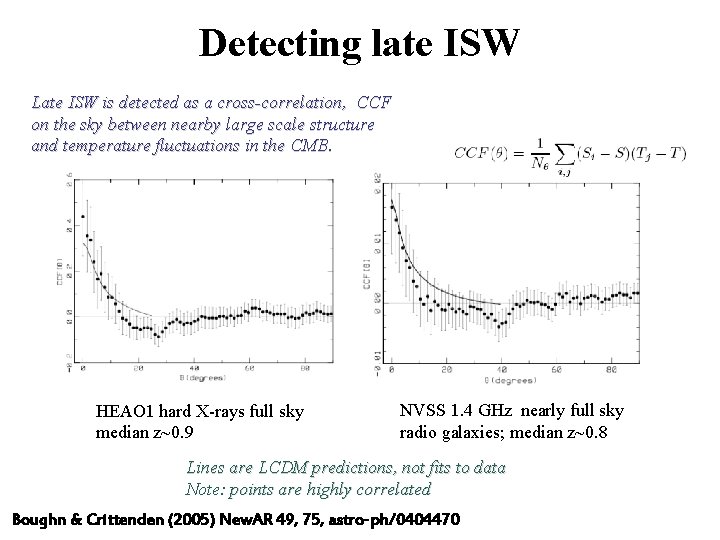
Detecting late ISW Late ISW is detected as a cross-correlation, CCF on the sky between nearby large scale structure and temperature fluctuations in the CMB. HEAO 1 hard X-rays full sky median z~0. 9 NVSS 1. 4 GHz nearly full sky radio galaxies; median z~0. 8 Lines are LCDM predictions, not fits to data Note: points are highly correlated Boughn & Crittenden (2005) New. AR 49, 75, astro-ph/0404470

Baryonic Acoustic Oscillations One wave around one center: Wave starts propagating at Big Bang; end at recombination. The final length is the sound crossing horizon at recomb. (Change of color means recombination. ) Many waves superimposed

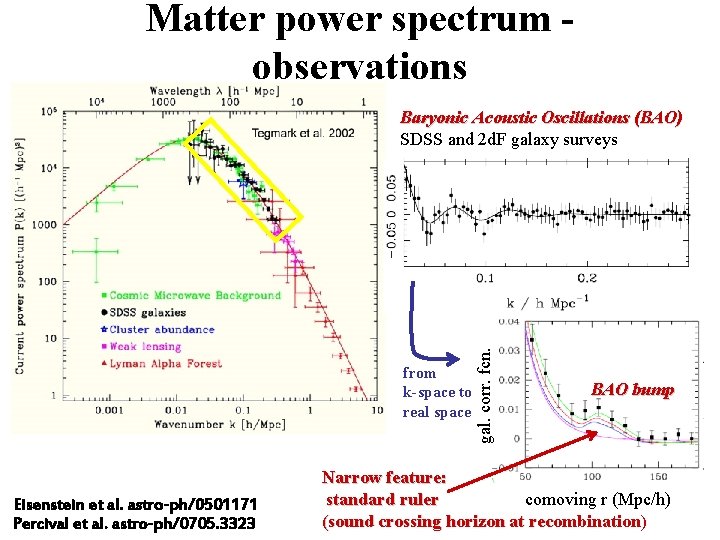
Matter power spectrum observations from k-space to real space Eisenstein et al. astro-ph/0501171 Percival et al. astro-ph/0705. 3323 gal. corr. fcn. Baryonic Acoustic Oscillations (BAO) SDSS and 2 d. F galaxy surveys BAO bump Narrow feature: standard ruler comoving r (Mpc/h) (sound crossing horizon at recombination)

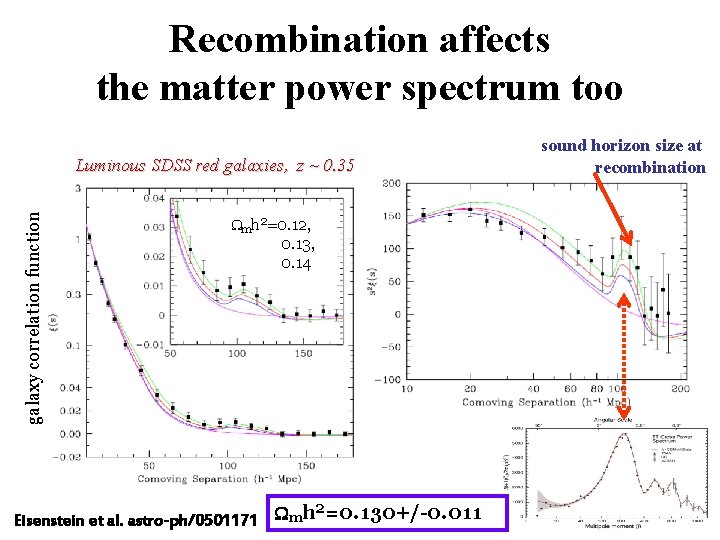
Recombination affects the matter power spectrum too galaxy correlation function Luminous SDSS red galaxies, z ~ 0. 35 Wmh 2=0. 12, 0. 13, 0. 14 2 Eisenstein et al. astro-ph/0501171 Wmh =0. 130+/-0. 011 sound horizon size at recombination

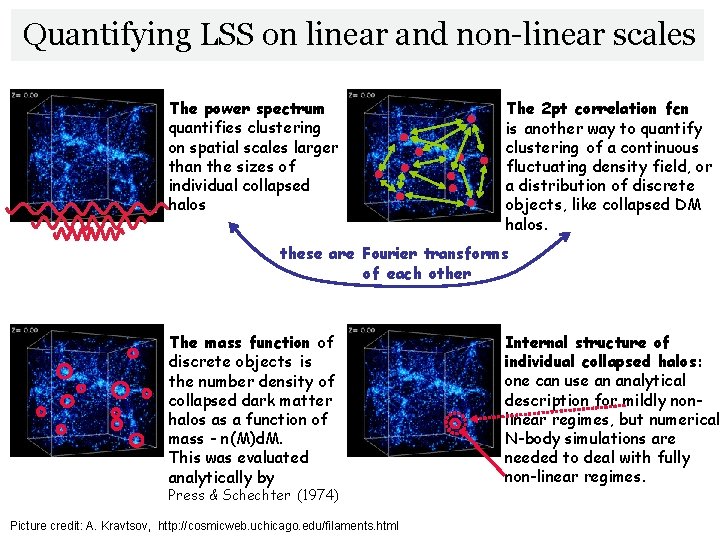
Quantifying LSS on linear and non-linear scales The power spectrum quantifies clustering on spatial scales larger than the sizes of individual collapsed halos The 2 pt correlation fcn is another way to quantify clustering of a continuous fluctuating density field, or a distribution of discrete objects, like collapsed DM halos. these are Fourier transforms of each other The mass function of discrete objects is the number density of collapsed dark matter halos as a function of mass - n(M)d. M. This was evaluated analytically by Press & Schechter (1974) Picture credit: A. Kravtsov, http: //cosmicweb. uchicago. edu/filaments. html Internal structure of individual collapsed halos: one can use an analytical description for mildly nonlinear regimes, but numerical N-body simulations are needed to deal with fully non-linear regimes.

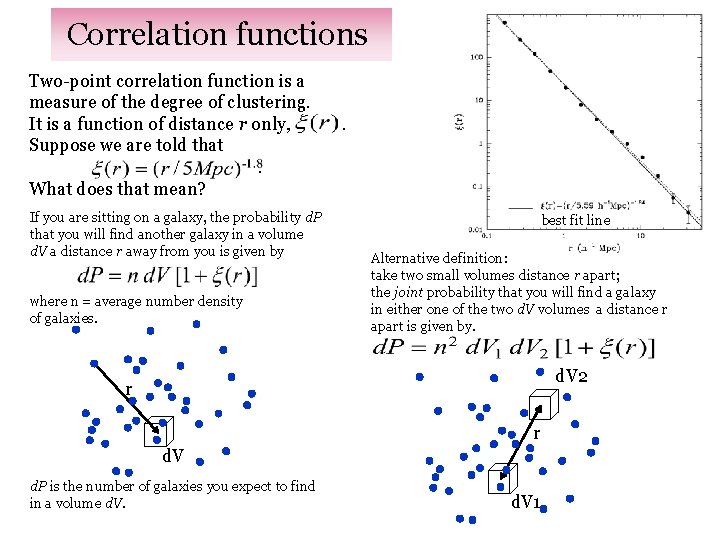
Correlation functions Two-point correlation function is a measure of the degree of clustering. It is a function of distance r only, Suppose we are told that. What does that mean? If you are sitting on a galaxy, the probability d. P that you will find another galaxy in a volume d. V a distance r away from you is given by where n = average number density of galaxies. . best fit line Alternative definition: take two small volumes distance r apart; the joint probability that you will find a galaxy in either one of the two d. V volumes a distance r apart is given by. d. V 2 r r d. V d. P is the number of galaxies you expect to find in a volume d. V 1

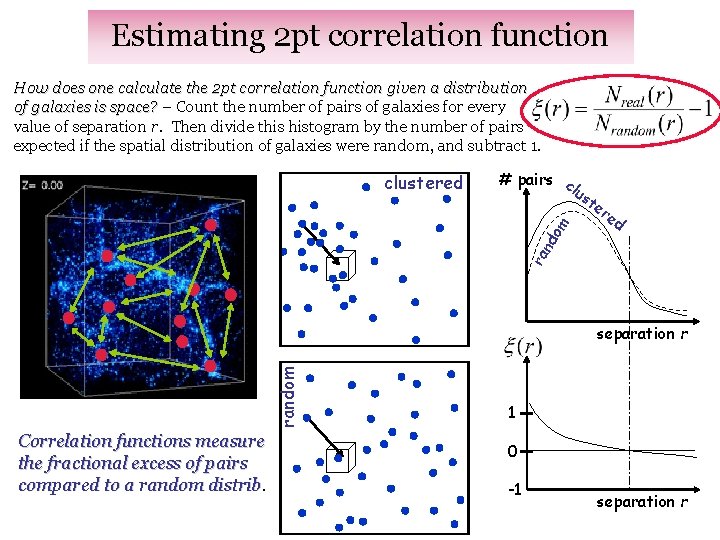
Estimating 2 pt correlation function How does one calculate the 2 pt correlation function given a distribution of galaxies is space? – Count the number of pairs of galaxies for every value of separation r. Then divide this histogram by the number of pairs expected if the spatial distribution of galaxies were random, and subtract 1. # pairs c lus te re d ra nd om clustered random separation r Correlation functions measure the fractional excess of pairs compared to a random distrib. 1 0 -1 separation r

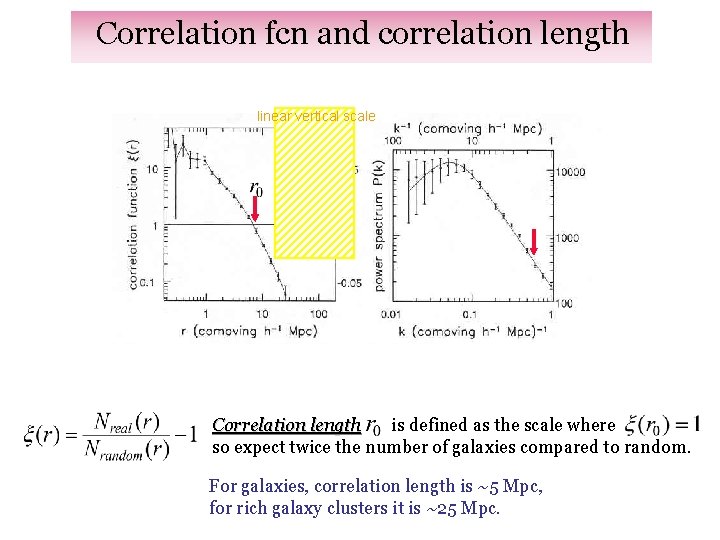
Correlation fcn and correlation length linear vertical scale Correlation length is defined as the scale where so expect twice the number of galaxies compared to random. For galaxies, correlation length is ~5 Mpc, for rich galaxy clusters it is ~25 Mpc.

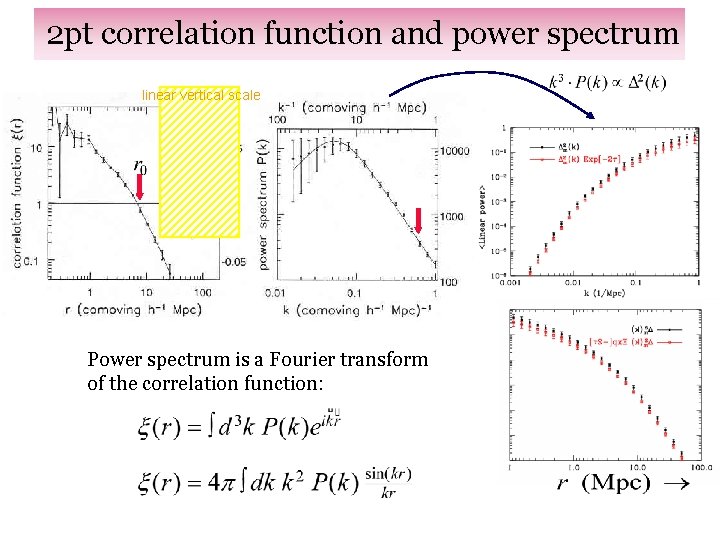
2 pt correlation function and power spectrum linear vertical scale Power spectrum is a Fourier transform of the correlation function:

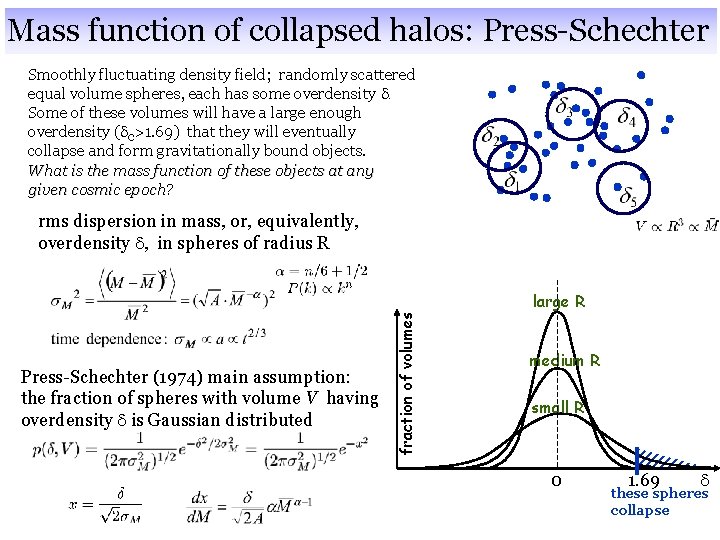
Mass function of collapsed halos: Press-Schechter Smoothly fluctuating density field; randomly scattered equal volume spheres, each has some overdensity d. Some of these volumes will have a large enough overdensity (dc>1. 69) that they will eventually collapse and form gravitationally bound objects. What is the mass function of these objects at any given cosmic epoch? Press-Schechter (1974) main assumption: the fraction of spheres with volume V having overdensity d is Gaussian distributed fraction of volumes rms dispersion in mass, or, equivalently, overdensity d, in spheres of radius R large R medium R small R 0 1. 69 d these spheres collapse

Mass function of collapsed halos: Press-Schechter The fraction of spheres that will eventually collapse is The fraction of spheres that have just collapsed ( of all possible M, but same dc) How much mass in every unit of volume is contained in these objects? How many of the collapsed objects are there? power law exponential

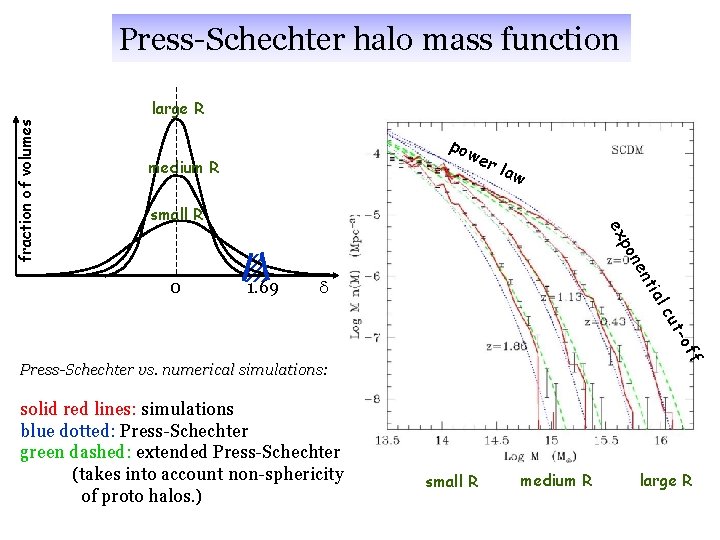
large R pow er medium R law small R 1. 69 d ut lc tia 0 en on p ex fraction of volumes Press-Schechter halo mass function -of f Press-Schechter vs. numerical simulations: solid red lines: simulations blue dotted: Press-Schechter green dashed: extended Press-Schechter (takes into account non-sphericity of proto halos. ) small R medium R large R

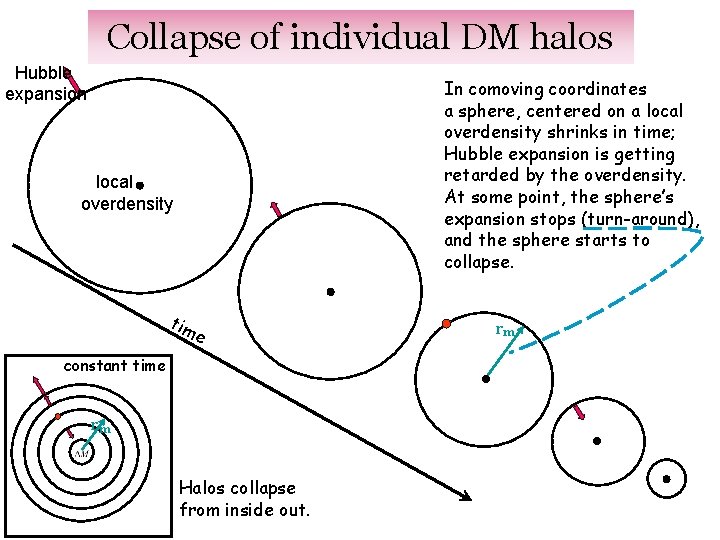
Collapse of individual DM halos Hubble expansion In comoving coordinates a sphere, centered on a local overdensity shrinks in time; Hubble expansion is getting retarded by the overdensity. At some point, the sphere’s expansion stops (turn-around), and the sphere starts to collapse. local overdensity tim e constant time rm Halos collapse from inside out. rm

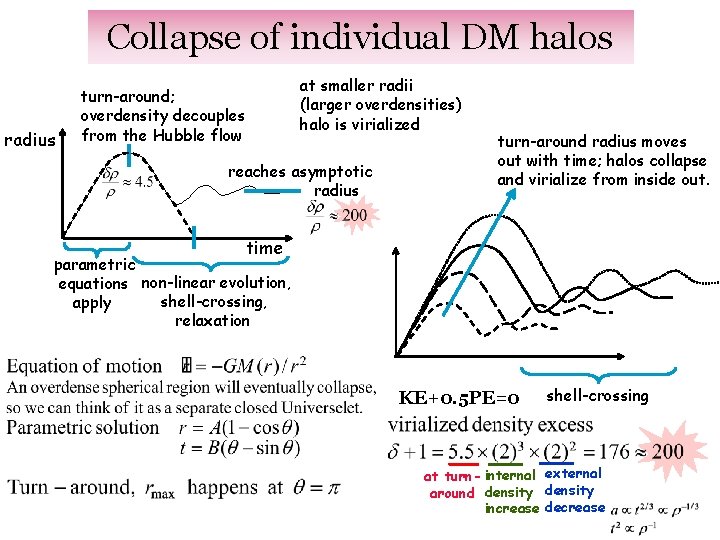
Collapse of individual DM halos radius turn-around; overdensity decouples from the Hubble flow at smaller radii (larger overdensities) halo is virialized reaches asymptotic radius turn-around radius moves out with time; halos collapse and virialize from inside out. time parametric equations non-linear evolution, shell-crossing, apply relaxation KE+0. 5 PE=0 shell-crossing at turn- internal external around density increase decrease

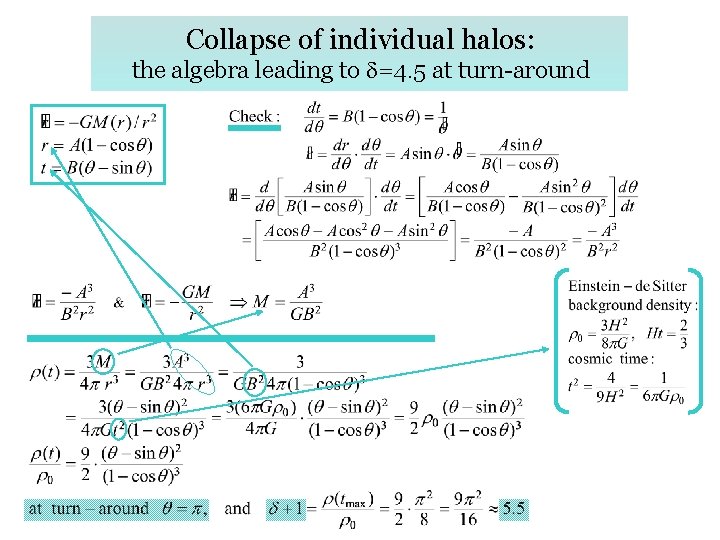
Collapse of individual halos: the algebra leading to d=4. 5 at turn-around

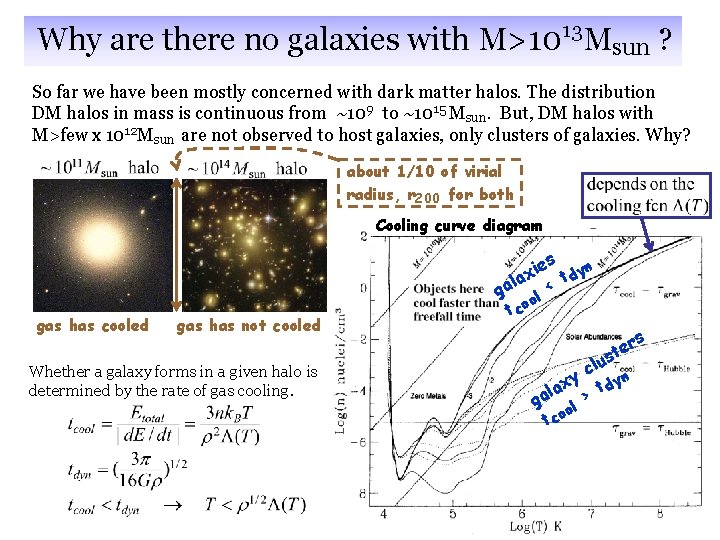
Why are there no galaxies with M>1013 Msun ? So far we have been mostly concerned with dark matter halos. The distribution DM halos in mass is continuous from ~109 to ~1015 Msun. But, DM halos with M>few x 1012 Msun are not observed to host galaxies, only clusters of galaxies. Why? about 1/10 of virial radius, r 200 for both Cooling curve diagram gas has cooled gas has not cooled Whether a galaxy forms in a given halo is determined by the rate of gas cooling. ies dyn x la < t a g ol t co rs ste clu n xy t dy a l ga ol > t co

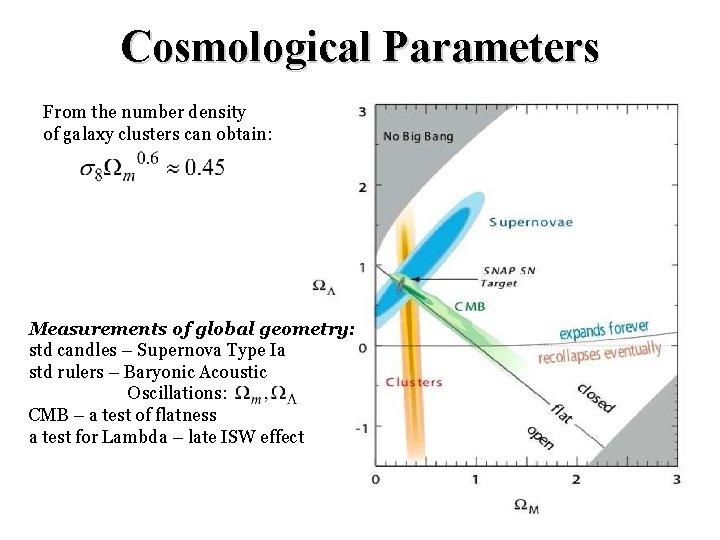
Cosmological Parameters From the number density of galaxy clusters can obtain: Measurements of global geometry: std candles – Supernova Type Ia std rulers – Baryonic Acoustic Oscillations: CMB – a test of flatness a test for Lambda – late ISW effect