Large networks clusters and Kronecker products Jure Leskovec

Large networks, clusters and Kronecker products Jure Leskovec (jure@cs. stanford. edu) Computer Science Department Cornell University / Stanford University Joint work with: Jon Kleinberg (Cornell), Christos Faloutsos (CMU), Michael Mahoney (Stanford), Kevin Lang (Yahoo), Anirban Dasgupta (Yahoo)

Rich data: Networks �Large on-line computing applications have detailed records of human activity: On-line communities: Facebook (120 million) Communication: Instant Messenger (~1 billion) News and Social media: Blogging (250 million) �We model the data as a network (an interaction graph) Can observe and study phenomena at scales not possible before Communication network

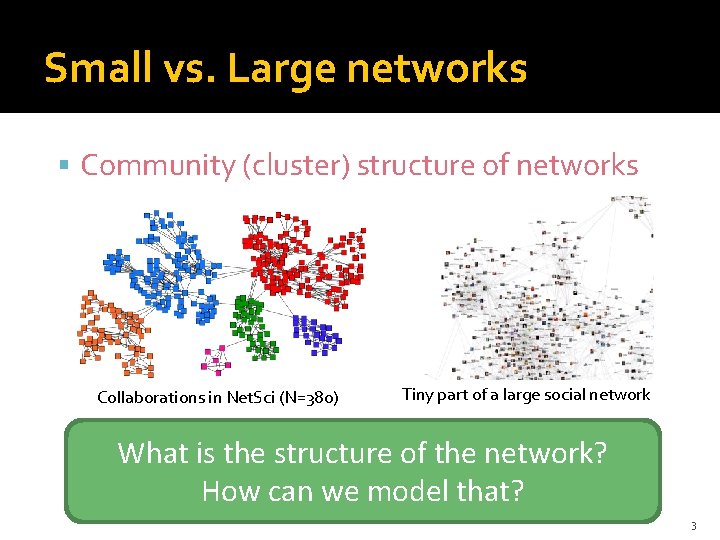
Small vs. Large networks Community (cluster) structure of networks Collaborations in Net. Sci (N=380) Tiny part of a large social network What is the structure of the network? How can we model that? 3

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] How expressed are communities? � How community like is a set of S nodes? � Idea: Use approximation algorithms for NP-hard graph partitioning problems as experimental probes of network structure. S’ Conductance (normalized cut): � Small Φ(S) == more community-like sets of nodes 4

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] Network Community Profile Plot �We define: Network community profile (NCP) plot Plot the score of best community of size k k=5 k=7 log Φ(k) Φ(5)=0. 25 Φ(7)=0. 18 Community size, log k 5

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] NCP plot: Network Science �Collaborations between scientists in Networks Conductance, log Φ(k) [Newman, 2005] Community size, log k 6

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] NCP plot: Large network �Typical example: General relativity collaboration network (4, 158 nodes, 13, 422 edges) 7

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] More NCP plots of networks 8

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] Φ(k), (conductance) NCP: Live. Journal (n=5 m, e=42 m) Better and better communities Communities get worse and worse Best community has ~100 nodes k, (community size) 9

[w/ Mahoney, Lang, Dasgupta, WWW ’ 08] Community size is bounded! Practically constant! �Each dot is a different network 10

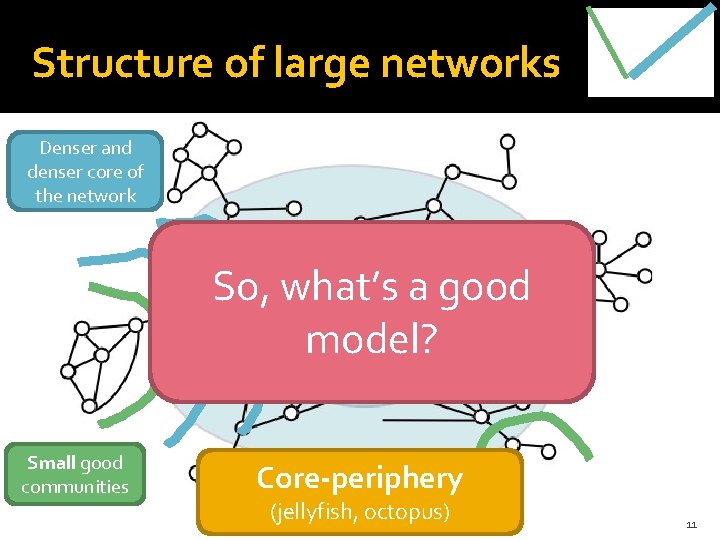
Structure of large networks Denser and denser core of the network Core contains So, what’s a good ~60% nodes and ~80% edges model? Small good communities Core-periphery (jellyfish, octopus) 11

[w/ Chakrabarti-Kleinberg-Faloutsos, PKDD ’ 05] Kronecker product: Definition �Kronecker product of matrices A and B is given by Nx. M Kx. L N*K x M*L �We define a Kronecker product of two graphs as a Kronecker product of their adjacency matrices 12

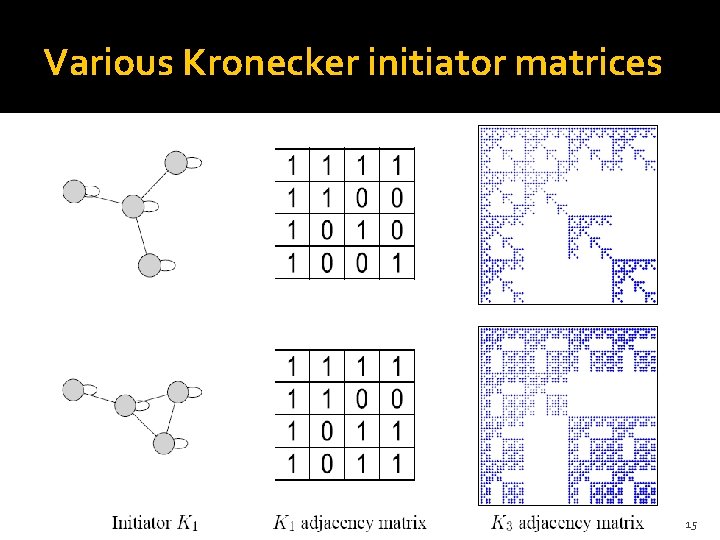
[w/ Chakrabarti-Kleinberg-Faloutsos, PKDD ’ 05] Kronecker graphs � Kronecker graph: a growing sequence of graphs by iterating the Kronecker product � Each Kronecker multiplication exponentially increases the size of the graph � One can easily use multiple initiator matrices (G 1’, G 1’’’ ) that can be of different sizes 13

[w/ Chakrabarti, Kleinberg, Faloutsos, PKDD ’ 05] Kronecker graphs Edge probability pij (3 x 3) Initiator (9 x 9) (27 x 27) Starting intuition: Recursion & self-similarity �Kronecker graphs mimic real networks: Theorem: Power-law degree distribution, Densification, Shrinking/stabilizing diameter, Spectral properties 14

Various Kronecker initiator matrices 15

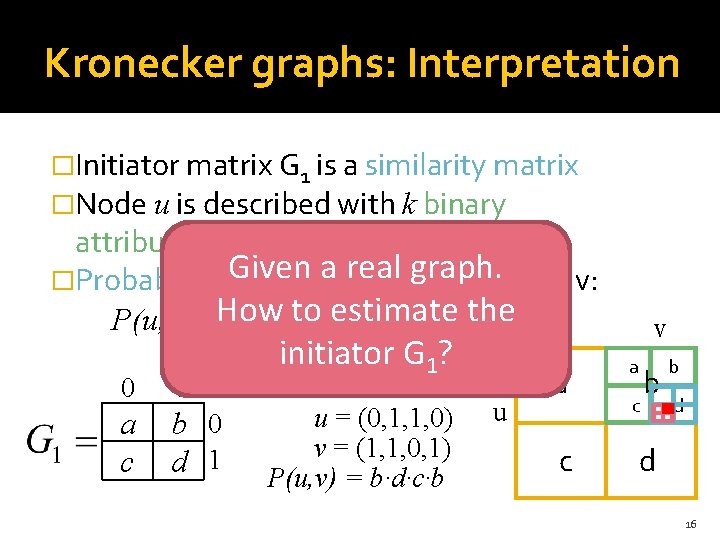
Kronecker graphs: Interpretation �Initiator matrix G 1 is a similarity matrix �Node u is described with k binary attributes: u 1, u 2 , …, uk Given real graph. �Probability of a linkabetween nodes u, v: the P(u, v) =How ∏ G 1 to [ui, estimate v i] 0 1 a c b 0 d 1 initiator G 1? u = (0, 1, 1, 0) v = (1, 1, 0, 1) P(u, v) = b∙d∙c∙b u a c v a c b b d d 16

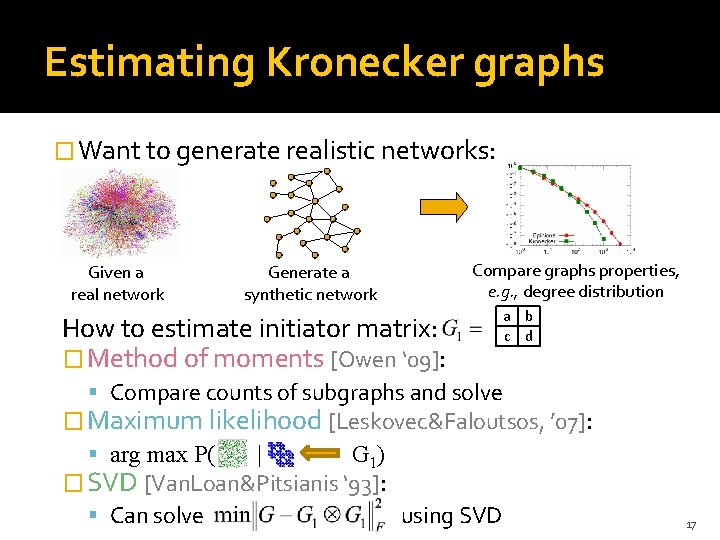
Estimating Kronecker graphs � Want to generate realistic networks: Given a real network Generate a synthetic network Compare graphs properties, e. g. , degree distribution How to estimate initiator matrix: � Method of moments [Owen ‘ 09]: a b c d Compare counts of subgraphs and solve � Maximum likelihood [Leskovec&Faloutsos, ’ 07]: arg max P( | G 1) � SVD [Van. Loan&Pitsianis ‘ 93]: Can solve using SVD 17

[w/ Dasgupta-Lang-Mahoney, WWW ’ 08] Kronecker & Network structure �What do estimated parameters tell us about the network structure? b edges a b c d a edges d edges c edges 18

[w/ Dasgupta-Lang-Mahoney, WWW ’ 08] Kronecker & Network structure �What do estimated parameters tell us about the network structure? 0. 9 0. 5 0. 1 0. 5 edges Core 0. 9 edges Periphery 0. 1 edges 0. 5 edges Core-periphery (jellyfish, octopus) 19

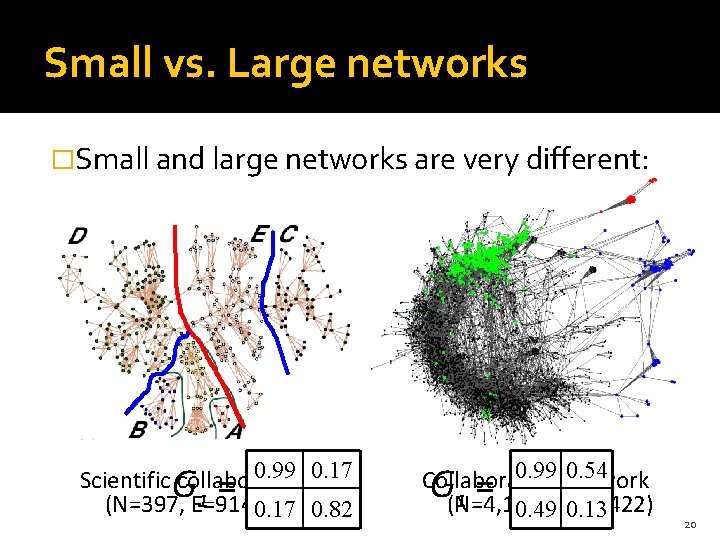
Small vs. Large networks �Small and large networks are very different: 0. 99 0. 17 Scientific collaborations 1 (N=397, E=914) 0. 17 0. 82 G = 0. 99 network 0. 54 Collaboration 1 (N=4, 158, 0. 49 E=13, 422) 0. 13 G = 20

Conclusion � Computational tools as probes into the structure of large networks � Community structure of large networks: Core-periphery structure Scale to natural community size: Dunbar number � Model: Kronecker graphs Analytically tractable: provable properties Can efficiently estimate parameters from data � Implications: No large clusters: no/little hierarchical structure Can’t be well embedded – no underlying geometry 21

Reflections �Why are networks the way they are? �Only recently have basic properties been observed on a large scale Confirms social science intuitions; calls others into question �What are good tractable network models? Builds intuition and understanding �Benefits of working with large data Observe structures not visible at smaller scales 22

jure@cs. stanford. edu http: //cs. stanford. edu/~jure

References � Graphs over Time: Densification Laws, Shrinking Diameters and Possible Explanations, by J. Leskovec, J. Kleinberg, C. Faloutsos, KDD 2005 � Realistic, Mathematically Tractable Graph Generation and Evolution, Using Kronecker Multiplication, by J. Leskovec, D. Chakrabarti, J. Kleinberg and C. Faloutsos, PKDD 2005 � Scalable Modeling of Real Graphs using Kronecker Multiplication, by J. Leskovec and C. Faloutsos, ICML 2007 � Statistical Properties of Community Structure in Large Social and Information Networks, by J. Leskovec, K. Lang, A. Dasgupta, M. Mahoney, WWW 2008 � Community Structure in Large Networks: Natural Cluster Sizes and the Absence of Large Well-Defined Clusters, by J. Leskovec, K. Lang, A. Dasgupta, M. Mahoney, Arxiv 2008 24