Laplace Transformations Dr Holbert February 25 2008 Lect

Laplace Transformations Dr. Holbert February 25, 2008 Lect 10 EEE 202 1

Sinusoids • Period: T = 2 p/ω = 1/f – Time necessary to go through one cycle • Frequency: f = 1/T – Cycles per second (Hertz, Hz) • Angular frequency: ω = 2 p f – Radians per second • Amplitude: A – For example, could be volts or amps Lect 10 EEE 202 2

Example Sinusoid • What is the amplitude, period, frequency, and angular (radian) frequency of this sinusoid? Lect 10 EEE 202 3

Phasors • A phasor is a complex number that represents the magnitude and phase angle of a sinusoidal signal: Lect 10 EEE 202 4

Complex Numbers imaginary axis • x is the real part • y is the imaginary part • z is the magnitude z y q x Lect 10 real axis EEE 202 • θ is the phase angle 5

More Complex Numbers • Polar coordinates: A = z θ • Rectangular coordinates: A = x + jy • Polar ↔ rectangular conversion relations: Lect 10 EEE 202 6

Arithmetic with Complex Numbers • To compute phasor voltages and currents, we need to be able to perform basic computations with complex numbers – Addition – Subtraction – Multiplication – Division • Appendix A has a review of complex numbers Lect 10 EEE 202 7

Complex Number Addition and Subtraction • Addition is most easily performed in rectangular coordinates: A = x + jy B = z + jw A + B = (x + z) + j(y + w) • Subtraction is also most easily performed in rectangular coordinates: A - B = (x - z) + j(y - w) Lect 10 EEE 202 8

Complex Number Multiplication and Division • Multiplication is most easily performed in polar coordinates: A = AM q B = BM f A B = (AM BM) (q + f) • Division is also most easily performed in polar coordinates: A / B = (AM / BM) (q - f) Lect 10 EEE 202 9

Are You a Technology “Have”? • There is a good chance that your calculator will convert from rectangular to polar, and from polar to rectangular • Convert to polar: 3 + j 4 and – 3 – j 4 • Convert to rectangular: 2 45 & – 2 45 • Add: 3 30 + 5 20 • Determine the complex conjugate of the phasor: A = z θ Lect 10 EEE 202 10

Singularity Functions • Singularity functions are either not finite or don't have finite derivatives everywhere • The two singularity functions of interest are 1. unit step function, u(t) and its construct: the gate function 2. delta or unit impulse function, (t) and its construct: the sampling function Lect 10 EEE 202 11

Unit Step Function, u(t) • The unit step function, u(t) – Mathematical definition – Graphical illustration u(t) 1 t 0 Lect 10 EEE 202 12

Extensions of Unit Step Function • A more general unit step function is u(t-a) 1 0 t a • The gate function can be constructed from u(t) – a rectangular pulse that starts at t= and ends at t= +T : u(t- ) – u(t- -T) – like an on/off switch Lect 10 EEE 202 1 0 +T t 13
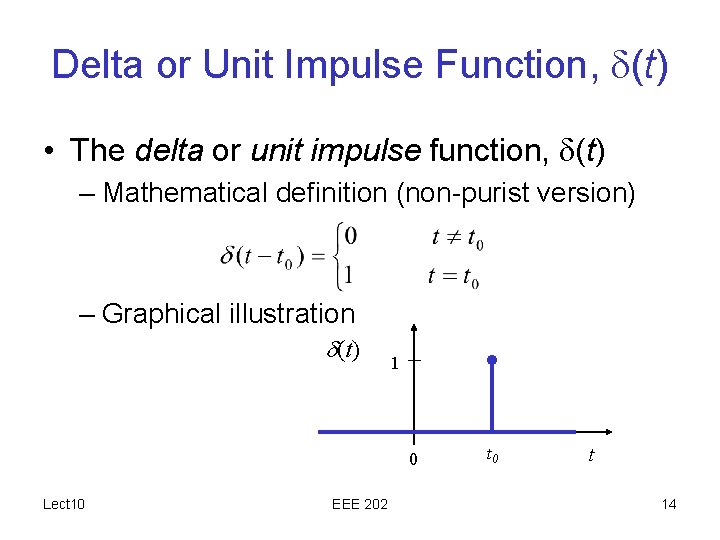
Delta or Unit Impulse Function, (t) • The delta or unit impulse function, (t) – Mathematical definition (non-purist version) – Graphical illustration (t) 1 0 Lect 10 EEE 202 t 0 t 14
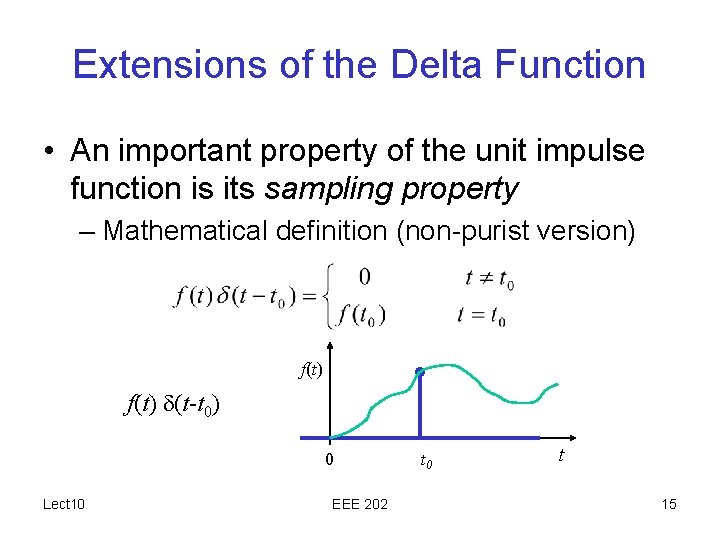
Extensions of the Delta Function • An important property of the unit impulse function is its sampling property – Mathematical definition (non-purist version) f(t) (t-t 0) 0 Lect 10 EEE 202 t 0 t 15

Laplace Transform • Applications of the Laplace transform – solve differential equations (both ordinary and partial) – application to RLC circuit analysis • Laplace transform converts differential equations in the time domain to algebraic equations in the frequency domain, thus three important processes: 1. transformation from the time to frequency domain 2. manipulate the algebraic equations to form a solution 3. inverse transformation from the frequency to time domain (we’ll wait to the next class time for this) Lect 10 EEE 202 16

Definition of Laplace Transform • Definition of the unilateral (one-sided) Laplace transform where s= +j is the complex frequency, and f(t)=0 for t<0 • The inverse Laplace transform requires a course in complex variable analysis (e. g. , MAT 461) Lect 10 EEE 202 17

Laplace Transform Pairs Most of the time we find Laplace transforms from tables like Table 5. 1 rather than using the defining integral Lect 10 EEE 202 18
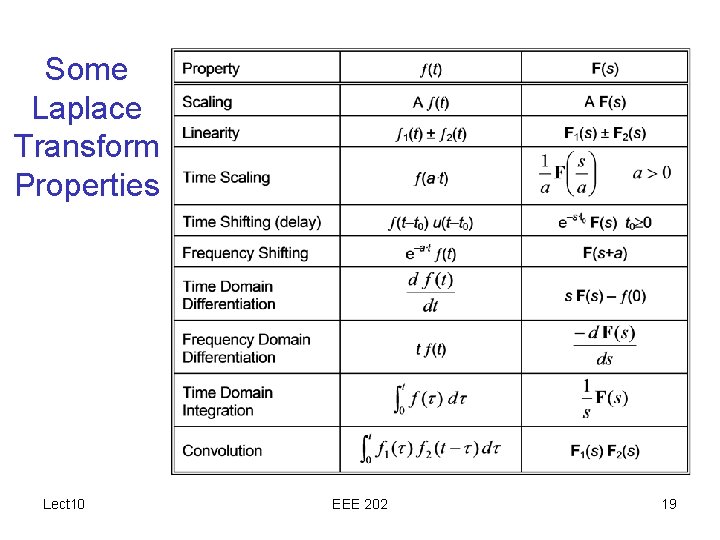
Some Laplace Transform Properties Lect 10 EEE 202 19

Class Examples • Drill Problem P 5 -2 (solve using both the defining Laplace integral, and the table of integrals with appropriate properties) Lect 10 EEE 202 20
- Slides: 20