Language Proof and Logic Formal Proofs and Boolean

Language, Proof and Logic Formal Proofs and Boolean Logic Chapter 6

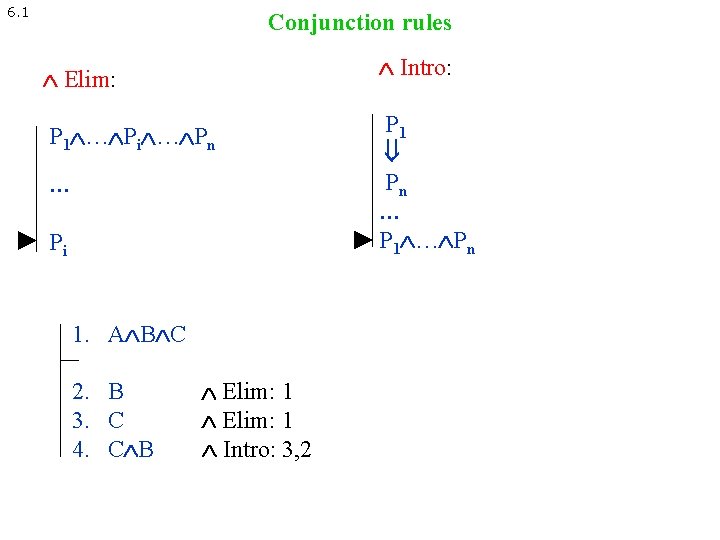
6. 1 Conjunction rules Elim: Intro: P 1 … Pi … Pn P 1 Pn … P 1 … Pn … Pi 1. A B C 2. B 3. C 4. C B Elim: 1 Intro: 3, 2

6. 2 a Disjunction rules Intro: Elim: Pi P 1 … Pn … … P 1 … Pi … Pn P 1 … S Pn … S

6. 2 b Example 1. (A B) (C D) 2. A B 3. B 4. B D Elim: 2 Intro: 3 5. C D 6. D 7. B D 8. B D Elim: 5 Intro: 6 Elim: 1, 2 -4, 5 -7 You try it, page 152

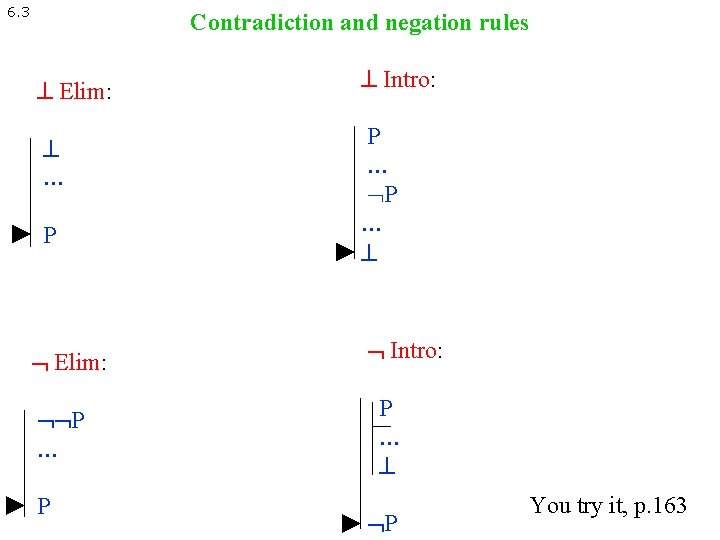
6. 3 Contradiction and negation rules Elim: Intro: … P … P Elim: P … P Intro: P … P You try it, p. 163

6. 4 The proper use of subproofs A subproof may use any of its own assumptions and derived sentences, as well as those of its parent (or grandparent, etc. ) proof. However, once a subproof ends, its statements are discharged. That is, nothing outside that subproof (say, in its parent or sibling proof) can cite anything from within that subproof.

6. 5 Strategy and tactics When looking for a proof, the following would help: 1. Understand what the sentences are saying. 2. Decide whether you think the conclusion follows from the premises. 3. If you think it does not follow, look for a counterexample. 4. If you think it does follow, try to give an informal proof first, and then turn it into a formal one. 5. Working backwards is always a good idea. 6. When working backwards, though, always check that your intermediate goals are consequences of the available information. You try it, page 170.

6. 6 Proofs without premises The conclusion of such a proof is always logically valid! 1. P P 2. P 3. P 4. 5. (P P) Elim: 1 Intro: 2, 3 Intro: 1 -4