Langage Relationnel Graphe de Requtes Prsentation Bas sur

Langage Relationnel Graphe de Requêtes

Présentation • Basé sur la théorie des ensembles – relations , opérateurs et opérandes – Opérateurs : relationnels, de test (<, >, = , …) et booléens (ET, OU, NON) – Opérandes : constantes ou variables • Recherche d’informations sur les relations par langage algébrique – Résultat d’une recherche : relation – Base du langage SQL GRAPHE DES REQUETES 2

Opérateurs relationnels • Opérateurs unaires – Sélection – Projection • Opérateurs binaires – – – Union Intersection Opérateurs ensemblistes Différence Division Produit Cartésien jointure 3

Sélection • Définition – Une sélection appliquée sur la relation R 1[a 1, . . . , an], selon le prédicat p 1 (condition) donne une relation R 2[a 1, . . . , an] ayant les n-uplets satisfaisant la condition • Symbole utilisé R Prédicat de Sélection R 1 4

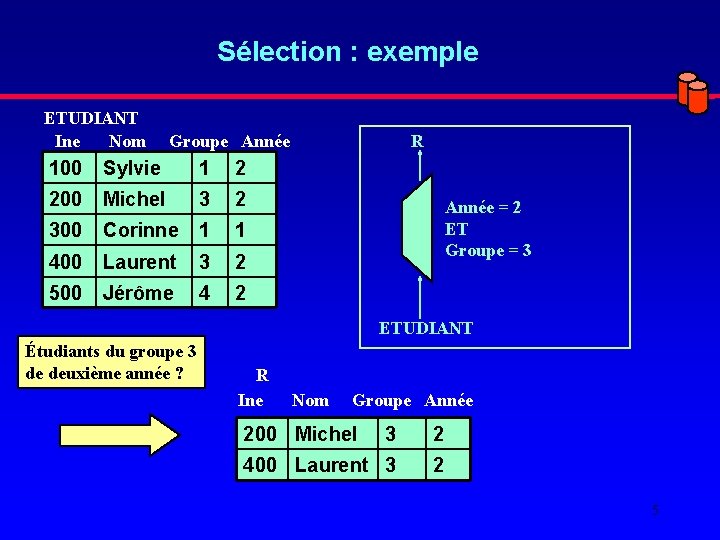
Sélection : exemple ETUDIANT Ine Nom Groupe Année 100 Sylvie 1 2 200 Michel 3 2 300 Corinne 1 1 400 Laurent 3 2 500 Jérôme 4 2 R Année = 2 ET Groupe = 3 ETUDIANT Étudiants du groupe 3 de deuxième année ? R Ine Nom Groupe Année 200 Michel 3 2 400 Laurent 3 2 5

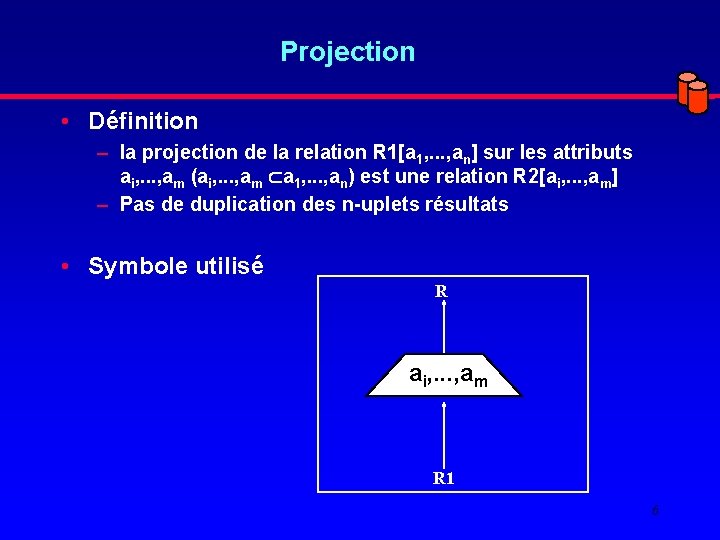
Projection • Définition – la projection de la relation R 1[a 1, . . . , an] sur les attributs ai, . . . , am (ai, . . . , am a 1, . . . , an) est une relation R 2[ai, . . . , am] – Pas de duplication des n-uplets résultats • Symbole utilisé R ai, . . . , am R 1 6

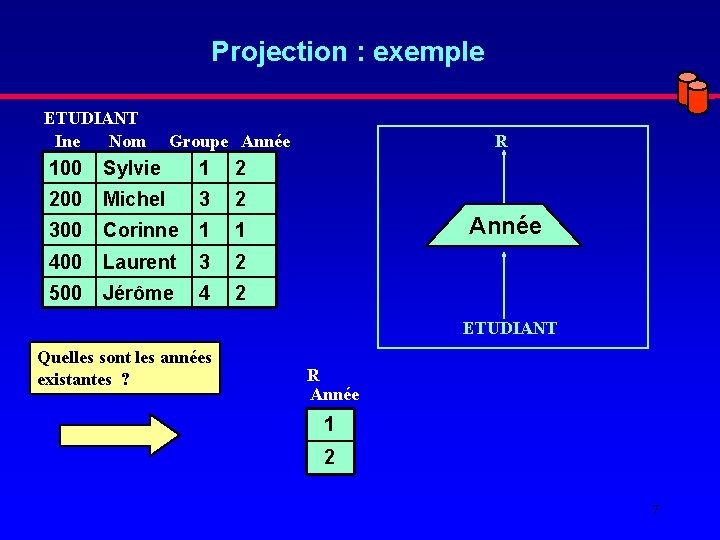
Projection : exemple ETUDIANT Ine Nom Groupe Année 100 Sylvie 1 2 200 Michel 3 2 300 Corinne 1 1 400 Laurent 3 2 500 Jérôme 4 2 R Année ETUDIANT Quelles sont les années existantes ? R Année 1 2 7

Union • Définition – Soient R 1[a 1, . . . , an] et R 2[b 1, . . . , bn] deux relations de même schéma , – Le résultat de l’union R contient les tuples de R 1 et les tuples de R 2 qui n’appartiennent pas à R 1 – Opérateur commutatif R R 1 U R 2 U • Symbole utilisé R 1 8

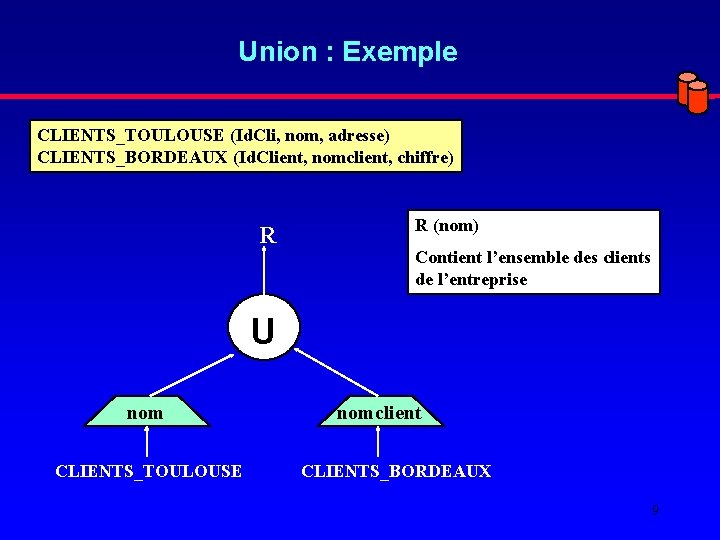
Union : Exemple CLIENTS_TOULOUSE (Id. Cli, nom, adresse) CLIENTS_BORDEAUX (Id. Client, nomclient, chiffre) R R (nom) Contient l’ensemble des clients de l’entreprise U nom CLIENTS_TOULOUSE nomclient CLIENTS_BORDEAUX 9

Intersection • Définition – Soient R 1[a 1, . . . , an] et R 2[b 1, . . . , bn] deux relations de même schéma – Le résultat de l’intersection R contient les tuples qui appartiennent, à la fois, à R 1 et R 2 – Opérateur commutatif R R 1 R 2 • Symbole utilisé R 1 10

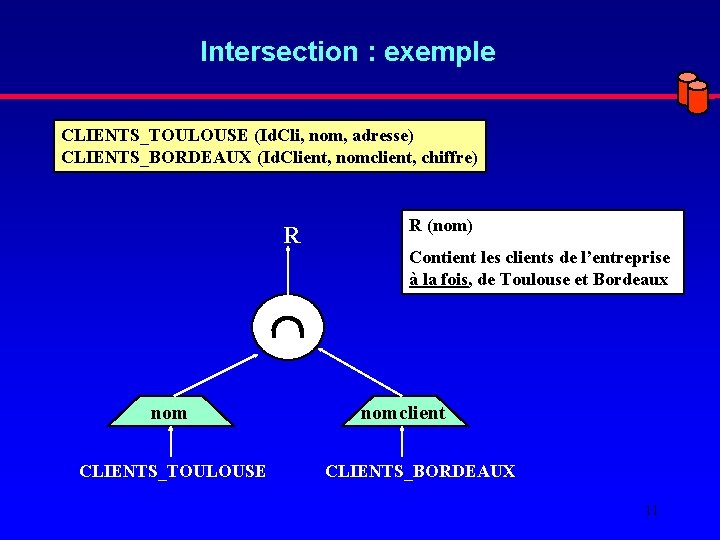
Intersection : exemple CLIENTS_TOULOUSE (Id. Cli, nom, adresse) CLIENTS_BORDEAUX (Id. Client, nomclient, chiffre) R R (nom) Contient les clients de l’entreprise à la fois, de Toulouse et Bordeaux nom CLIENTS_TOULOUSE nomclient CLIENTS_BORDEAUX 11

Différence • Définition – Soient R 1[a 1, . . . , an] et R 2[b 1, . . . , bn] deux relations de même schéma , – Le résultat de la différence R contient les tuples de R 1 qui n’appartiennent pas à R 2 – Opérateur non commutatif R R 1 U R 2 • Symbole utilisé R 1 12

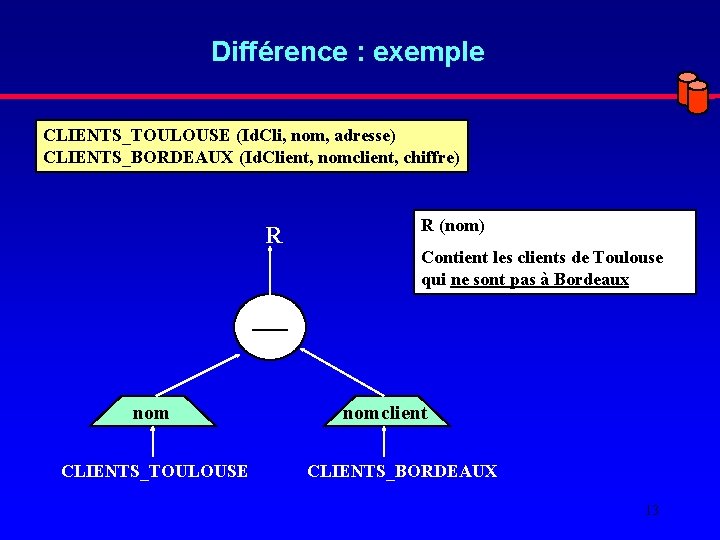
Différence : exemple CLIENTS_TOULOUSE (Id. Cli, nom, adresse) CLIENTS_BORDEAUX (Id. Client, nomclient, chiffre) R nom CLIENTS_TOULOUSE R (nom) Contient les clients de Toulouse qui ne sont pas à Bordeaux nomclient CLIENTS_BORDEAUX 13

Division • Définition – Soient R 1[a 1, . . . , an, b 1, . . . , bn] et R 2[b 1, . . . , bn] deux relations telles que la structure de R 2 soit incluse dans la structure de R 1 – R = résultat de la division de R 1 par R 2 – R est une relation de structure R[a 1, . . . , an] qui contient les tuples ti vérifiant : ti R (ti est un tuple de structure [a 1, . . . , an]) tj R 2 (tj est un tuple de structure [b 1, . . . , bn]) ti, tj R 1 (ti, tj est un tuple de structure [a 1, . . . , an, b 1, . . . , bn]) • Opérateur non commutatif • Sert à comparer un ensemble avec un autre ensemble (dit de référence) 14

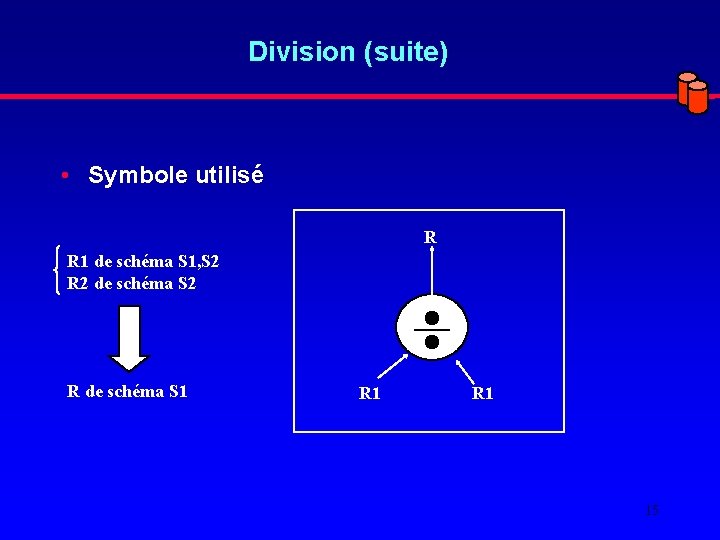
Division (suite) • Symbole utilisé R R 1 de schéma S 1, S 2 R 2 de schéma S 2 R de schéma S 1 R 1 15

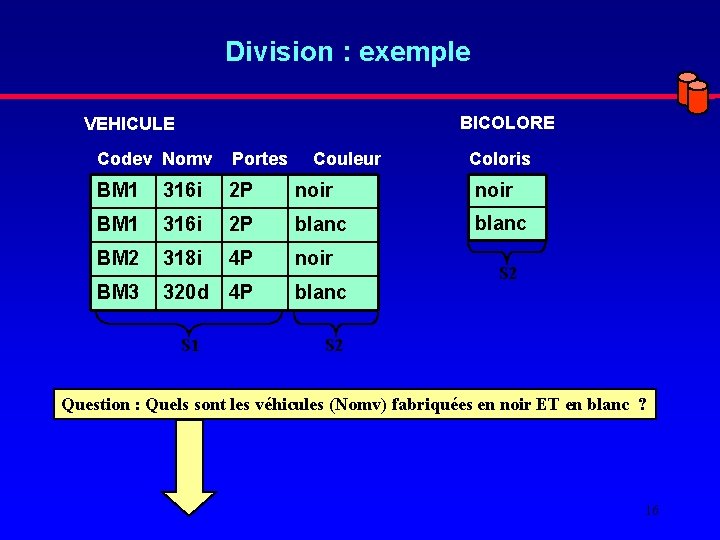
Division : exemple BICOLORE VEHICULE Codev Nomv Portes Couleur Coloris BM 1 316 i 2 P noir BM 1 316 i 2 P blanc BM 2 318 i 4 P noir BM 3 320 d 4 P blanc S 1 S 2 Question : Quels sont les véhicules (Nomv) fabriquées en noir ET en blanc ? 16

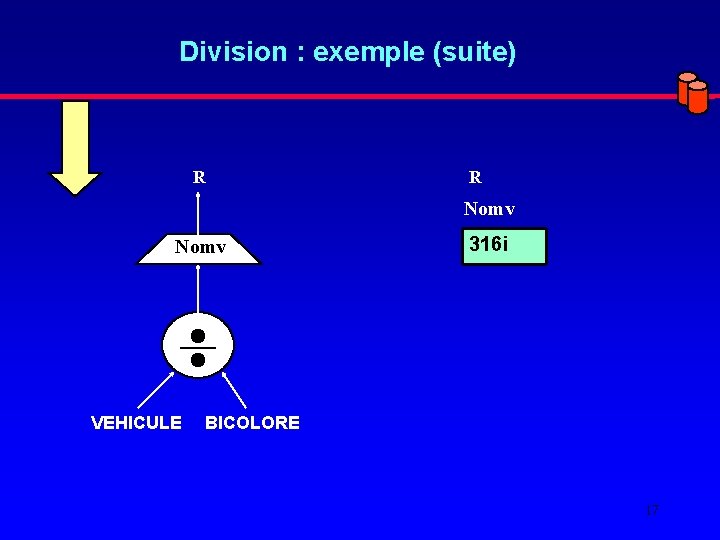
Division : exemple (suite) R R Nomv VEHICULE 316 i BICOLORE 17

Produit cartésien • Définition – Soient R 1[a 1, . . . , an] et R 2[b 1, . . . , bm] deux relations de schéma différent, R = résultat du produit R 1 R 2 – R est une relation de structure R 3[a 1, . . . , an, b 1, . . . , bm] qui contient les combinaisons des tuples de R 1 et R 2 • Opérateur commutatif R • Symbole utilisé R 1 18

Produit cartésien : exemple ETUDIANT MATIERE Ine Nom Id. M 100 Sylvie BD Bases de Données 200 Michel ACSI Analyse 300 Laurent MATH Mathématiques Nom. M Question : Créer la relation COURS (Ine, Id. M) sachant que chaque étudiant suit toutes les matières ? 19

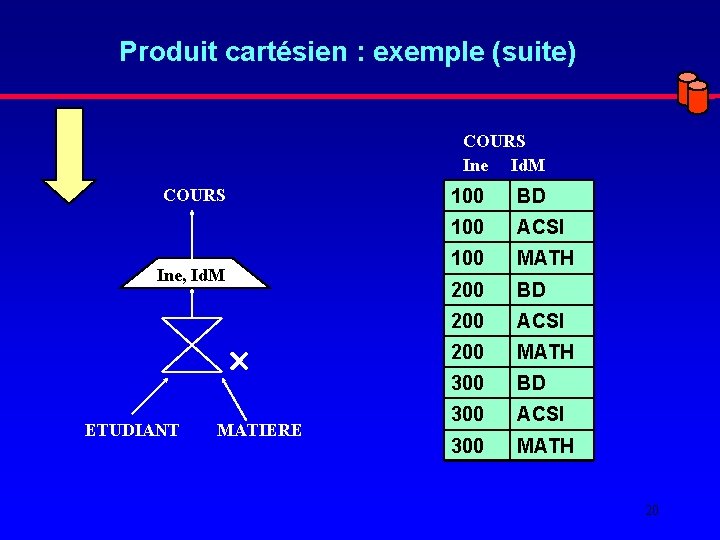
Produit cartésien : exemple (suite) COURS Ine Id. M COURS Ine, Id. M ETUDIANT MATIERE 100 BD 100 ACSI 100 MATH 200 BD 200 ACSI 200 MATH 300 BD 300 ACSI 300 MATH 20

Jointure • Définition – Soient R 1[a 1, . . . , an] et R 2[b 1, . . . , bm] deux relations, R = jointure de ces relations avec un prédicat – R[a 1, . . . , an, b 1, . . . , bm] contient les tuples de R 1 et de R 2 résultant un produit cartésien vérifiant le prédicat • Opérateur fondamental (basé sur les valeurs) • Le prédicat contient une clause de jointure et éventuellement d’autres conditions • Opérateur binaire commutatif 21

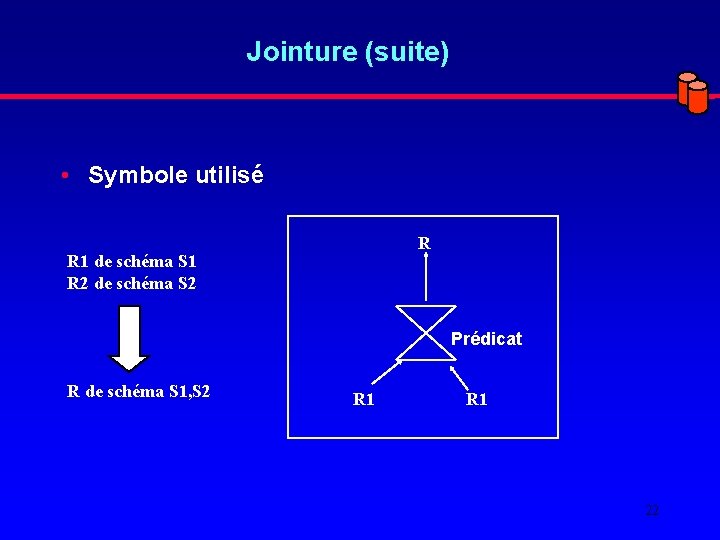
Jointure (suite) • Symbole utilisé R R 1 de schéma S 1 R 2 de schéma S 2 Prédicat R de schéma S 1, S 2 R 1 22

Jointure : exemple CLIENTS (Id. Cli, Nom, Adresse) OUVRAGES (Id. Ouv, Titre, Nbex) EMPRUNTS (Id. Cli#, Id. Ouv#, Date. Emp) Question : Nom et Adresse des clients ayant emprunté l’ouvrage ‘BD’ le ’ 10/10/2003’ ? 23

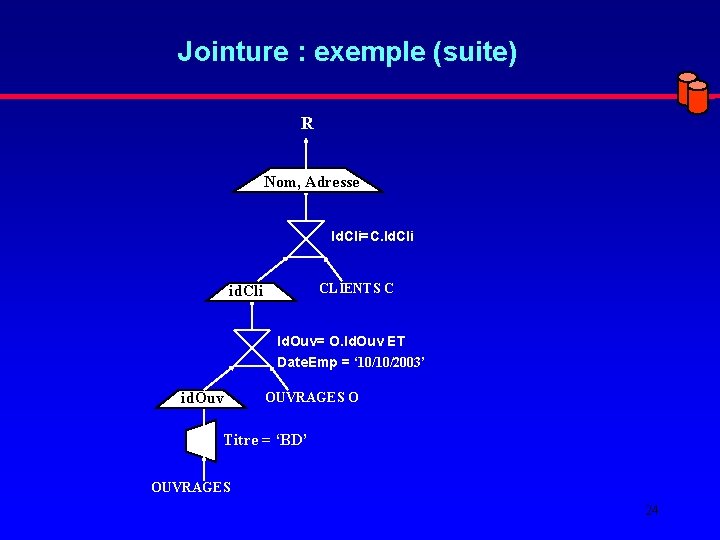
Jointure : exemple (suite) R Nom, Adresse Id. Cli=C. Id. Cli CLIENTS C id. Cli Id. Ouv= O. Id. Ouv ET Date. Emp = ‘ 10/10/2003’ id. Ouv OUVRAGES O Titre = ‘BD’ OUVRAGES 24

Graphe des requêtes et SGBD • Tous les SGBD R de type SQL mettent en œuvre un graphe de requêtes • Oracle fournit une table (plan_table) montrant le schéma global • Ce graphe permet d’optimiser les requêtes • Certains, comme SQL Server présentent ce graphe sous forme graphique 25

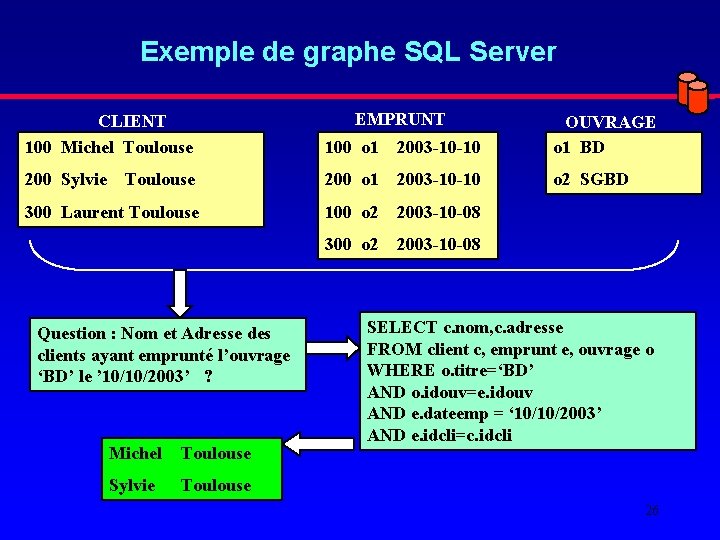
Exemple de graphe SQL Server EMPRUNT CLIENT 100 Michel Toulouse 100 o 1 2003 -10 -10 OUVRAGE o 1 BD 200 Sylvie Toulouse 200 o 1 2003 -10 -10 o 2 SGBD 300 Laurent Toulouse 100 o 2 2003 -10 -08 300 o 2 2003 -10 -08 Question : Nom et Adresse des clients ayant emprunté l’ouvrage ‘BD’ le ’ 10/10/2003’ ? Michel Toulouse Sylvie Toulouse SELECT c. nom, c. adresse FROM client c, emprunt e, ouvrage o WHERE o. titre=‘BD’ AND o. idouv=e. idouv AND e. dateemp = ‘ 10/10/2003’ AND e. idcli=c. idcli 26

Exemple de graphe SQL Server (suite) 27

Exemple de graphe SQL Server (suite) 28