Landau Theory Introduction Many phase transitions exhibit similar

Landau Theory • Introduction § Many phase transitions exhibit similar behaviors: critical temperature, order parameter… § Can one find a rather simple “unifying theory” that gives a general “phenomenological” overview of phase transitions ? § Several approaches : Molecular field (Weiss ~1925): solve the Schrödinger equation for a one particle system but with an effective interaction potential : Microscopic model (Ising 1924): solve the Schrödinger equation for “pseudo spins” on a lattice with effective interaction Hamiltonian restricted to first neighbors

Landau Theory • Introduction § Landau Theory : – Express a thermo dynamical potential as a function of the order parameter ( ), its conjugated external field (h) and temperature. – Keep close to a stable state minimum of energy power series expansion, eg. like: – Find and discuss minima of versus temperature and external field. – Look at thermodynamics’ properties (latent heat, specific heat, susceptibility, etc. ) in order to classify phase transitions

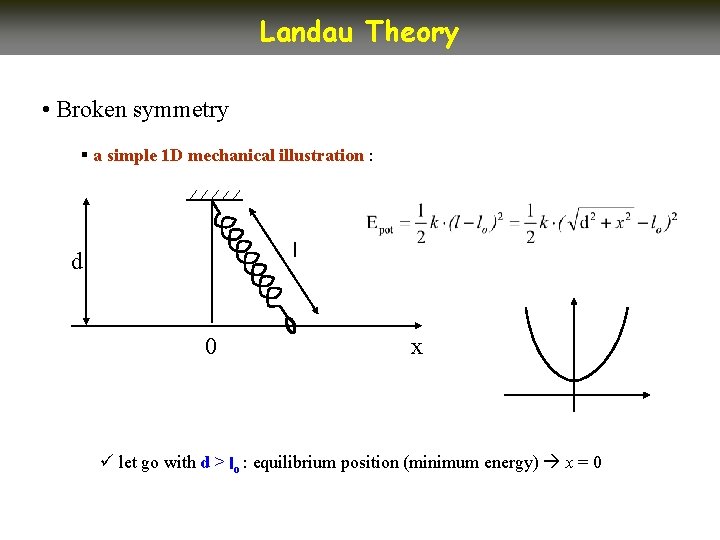
Landau Theory • Broken symmetry § a simple 1 D mechanical illustration : l d 0 x ü let go with d > lo : equilibrium position (minimum energy) x = 0

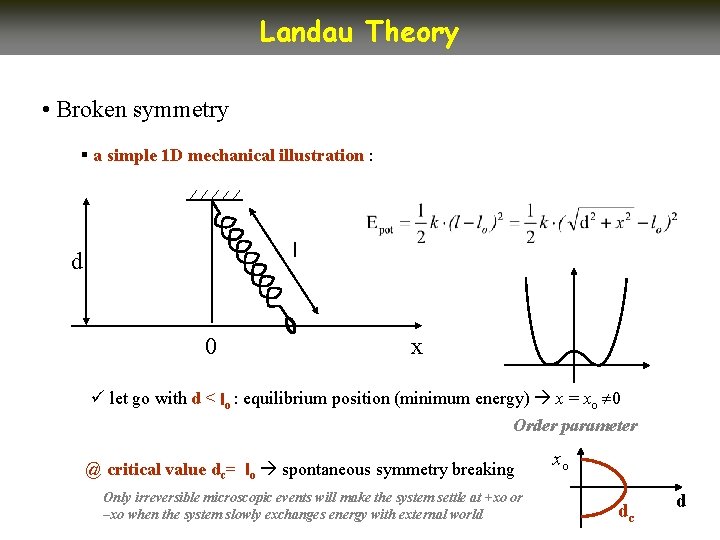
Landau Theory • Broken symmetry § a simple 1 D mechanical illustration : l d 0 x ü let go with d < lo : equilibrium position (minimum energy) x = xo 0 Order parameter @ critical value dc= lo spontaneous symmetry breaking Only irreversible microscopic events will make the system settle at +xo or –xo when the system slowly exchanges energy with external world xo dc d

Landau Theory • Broken symmetry § a simple 1 D mechanical illustration : l d 0 x ü Taylor expansion of potential (elastic) energy

Landau Theory • Broken symmetry § a simple 1 D mechanical illustration : l d 0 x ü Taylor expansion of potential (elastic) energy Change sign at d=dc !!! Does not change sign

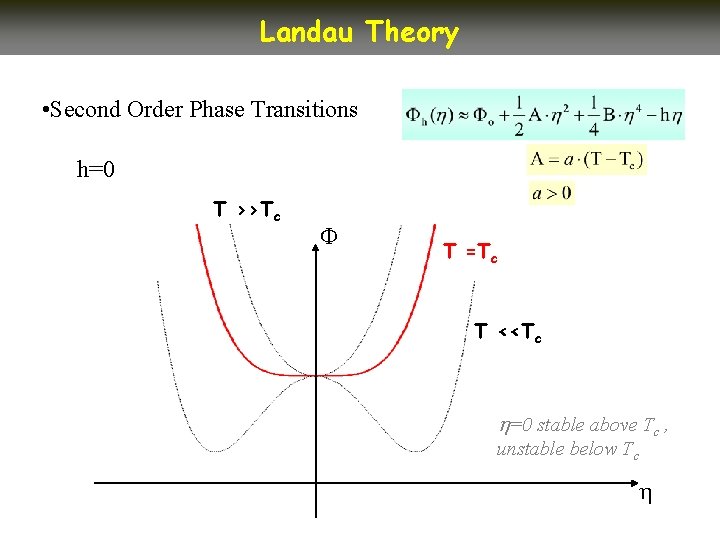
Landau Theory • Second Order Phase Transitions h=0 T >>Tc T =Tc T <<Tc =0 stable above Tc , unstable below Tc

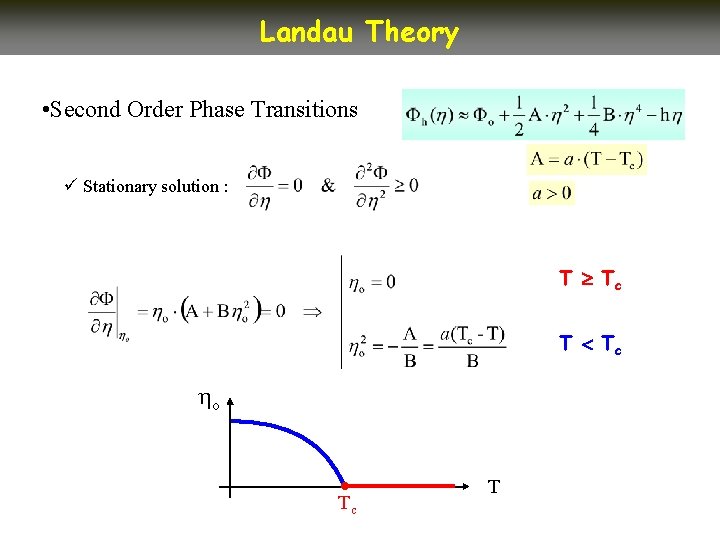
Landau Theory • Second Order Phase Transitions ü Stationary solution : T Tc o Tc T

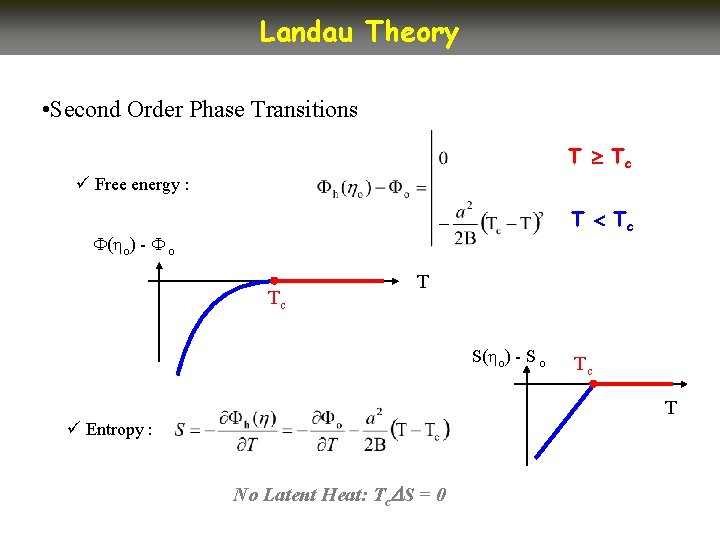
Landau Theory • Second Order Phase Transitions T Tc ü Free energy : T Tc ( o) - o Tc T S( o) - S o Tc T ü Entropy : No Latent Heat: Tc S = 0

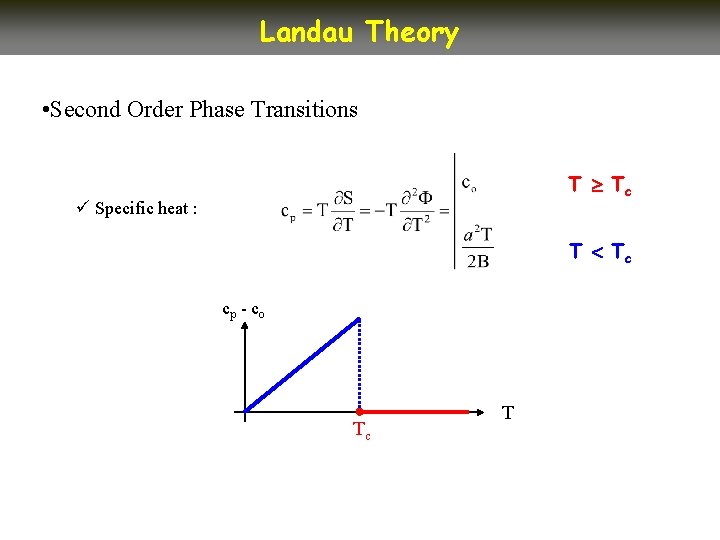
Landau Theory • Second Order Phase Transitions T Tc ü Specific heat : T Tc cp - co Tc T

Landau Theory • Second Order Phase Transitions ü Susceptibility : -1 T Tc Curie law Tc T

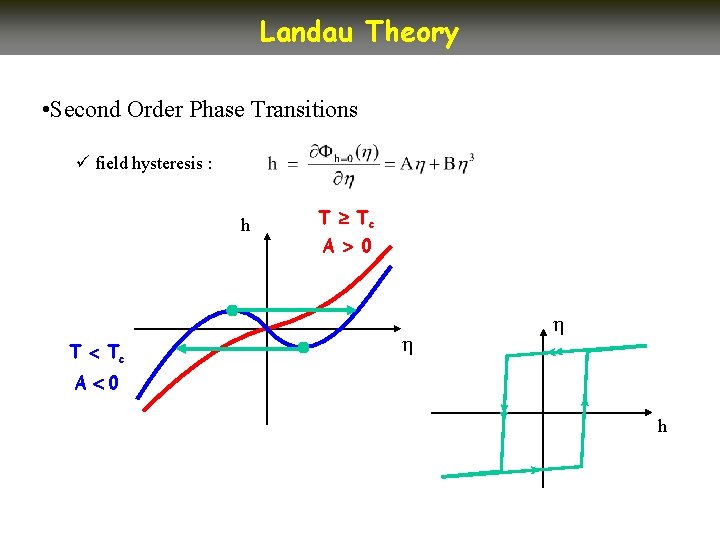
Landau Theory • Second Order Phase Transitions ü field hysteresis : h T Tc A 0 A 0 h

Landau Theory • Second Order Phase Transitions SUMMARY ü One critical temperature Tc ü No discontinuity of , , S (no latent heat) at Tc ü Jump of Cp at Tc ü Divergence of and at Tc ü Field hysteresis

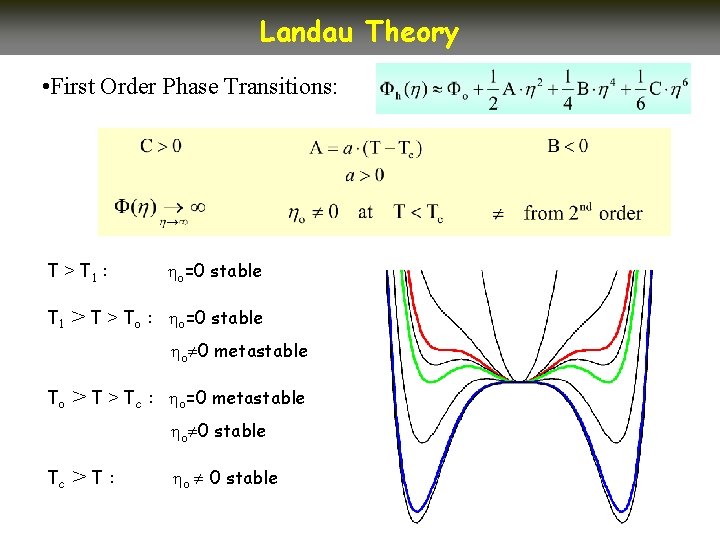
Landau Theory • First Order Phase Transitions: T > T 1 : T 1 > To : o=0 stable o 0 metastable To > Tc : o=0 metastable o 0 stable Tc >T: o 0 stable

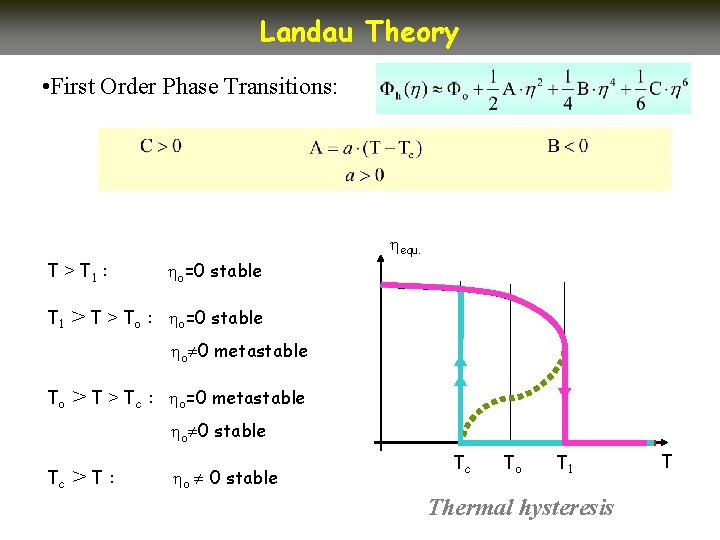
Landau Theory • First Order Phase Transitions: equ. T > T 1 : T 1 > To : o=0 stable o 0 metastable To > Tc : o=0 metastable o 0 stable Tc >T: o 0 stable Tc To T 1 Thermal hysteresis T

Landau Theory • First Order Phase Transitions: ü Steady state : T Tc +

Landau Theory • First Order Phase Transitions: ü Steady state : T = To

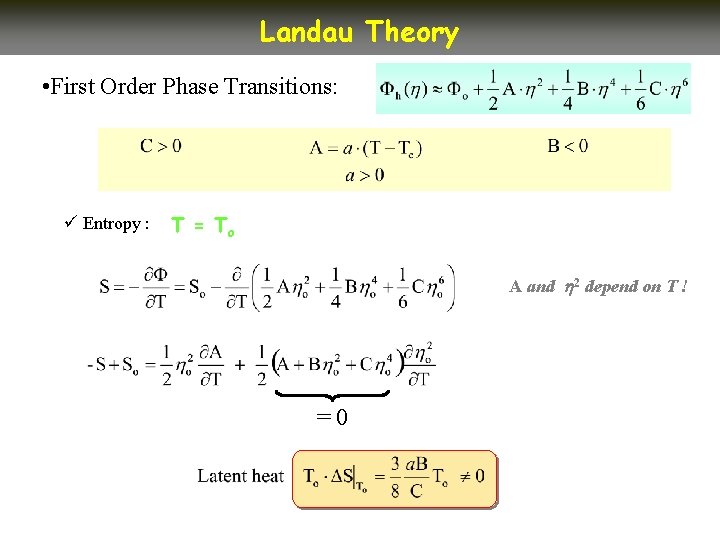
Landau Theory • First Order Phase Transitions: ü Entropy : T = To A and 2 depend on T ! =0

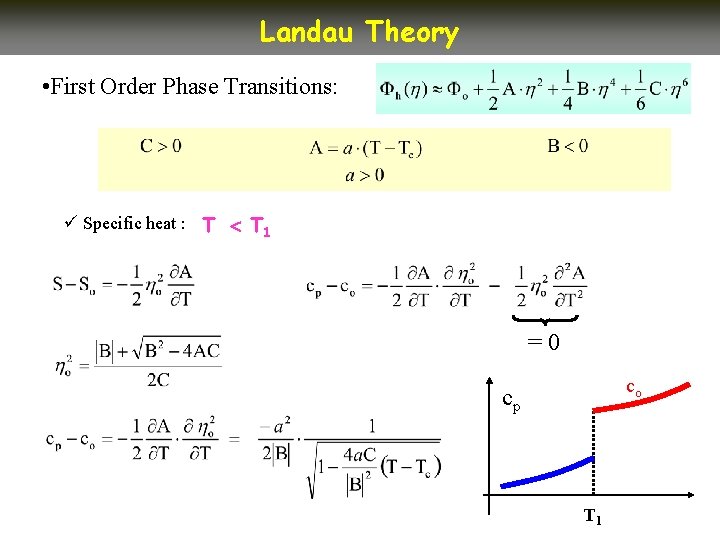
Landau Theory • First Order Phase Transitions: ü Specific heat : T T 1 =0 co cp T 1

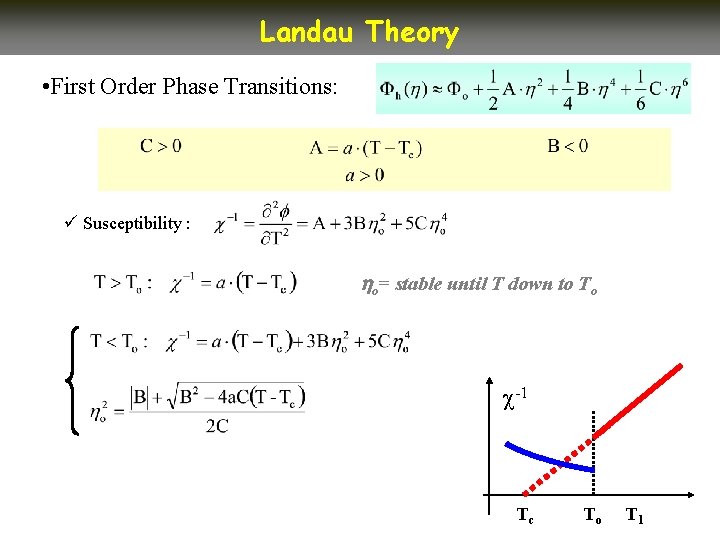
Landau Theory • First Order Phase Transitions: ü Susceptibility : o= stable until T down to To -1 Tc To T 1

Landau Theory • First Order Phase Transitions SUMMARY ü Existence of metastable phases ü Temperature domain (Tc T 1) for coexistence of high and low temperature phases ü at To (Tc < To < T 1) both high and low teperature phases are stable ü Temperature hysteresis ü Discontinuity of , , S (latent heat), Cp, at Tc

Landau Theory • Tricritical point In the formalism of first order phase transitions, it can happen that B parameter changes sign under the effect of an external field. Then there is a point, which is called tricritical point, where B=0. The Landau expansion then takes the following form: ü Equilibrium conditions :

Landau Theory • Tricritical point ü Potential : T>Tc: =0 Tc T>Tc: 0 T

Landau Theory • Tricritical point ü Entropy : A and 2 depend on T ! S T>Tc: =0 T>Tc: 0 Tc T

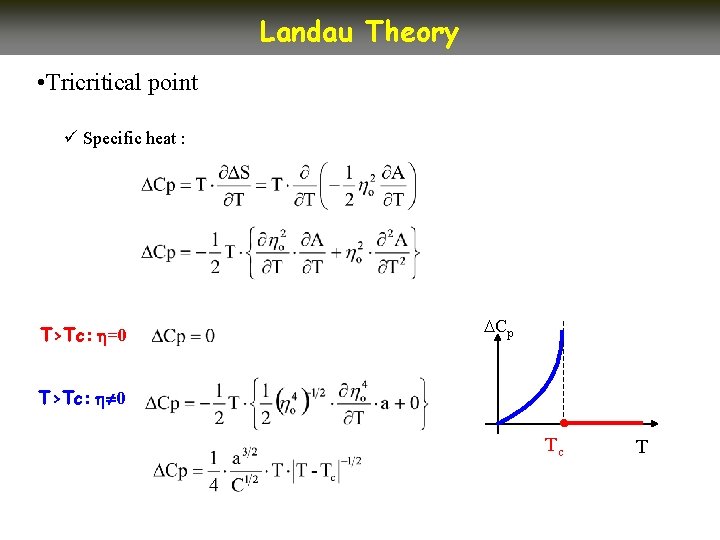
Landau Theory • Tricritical point ü Specific heat : T>Tc: =0 Cp T>Tc: 0 Tc T

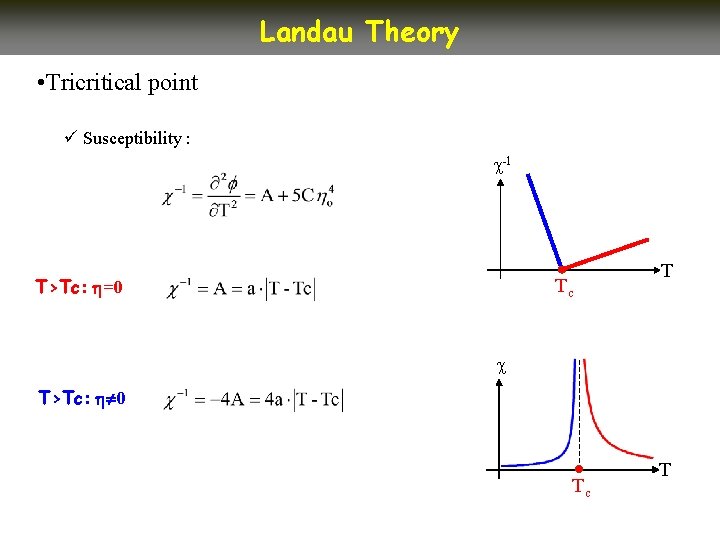
Landau Theory • Tricritical point ü Susceptibility : -1 T>Tc: =0 Tc T T>Tc: 0 Tc T