Lagrange petits points Cinq points la Lune 20090217

Lagrange à petits points Cinq points à la Lune 2009/02/17 Points de Lagrange

Historique Dans la mécanique classique, le mouvement de deux corps est parfaitement décrit par les lois de Képler. Les trajectoires sont des coniques dont tous les éléments sont connus. Johannes Kepler (1571 -1630) Le problème suivant est celui des trois corps. Newton n’est pas arrivé à le résoudre Newton Isaac (1643 -1727) 2009/02/17 Points de Lagrange 2

Historique En 1772 Euler et Lagrange se partagent le prix de l’Académie des sciences sur le problème des 3 corps Ils trouvent qu'il existe des positions pour un petit corps, où la résultante des forces est nulle. Léonhard Euler a découvert les points de stabilité appelés L 1, L 2 et L 3 dans le système Terre-Lune. Leonhard Euler 1707 -1783 Lagrange fait une analyse plus complète avec L 4 and L 5 Lagrange montre que le corps le plus massif doit être 25 fois plus lourds que l’autre. Essai sur le problème des trois corps. "Oeuvres / Joseph Louis de Lagrange. 6, page 229 -331 http: //gallica. bnf. fr/Metacata. htm 2009/02/17 Points de Lagrange Joseph-Louis Lagrange 1736 -1813 3

2009/02/17 Points de Lagrange 4

Historique Joseph Louis, comte de Lagrange (1736 -1813) Mathématicien. Passe 30 ans dans le Piémont, 21 ans à Berlin et le reste à Paris. Célèbre pour : Mécanique analytique, Mécanique céleste, analyse mathématiques, Théorie des nombres Souvenirs d’études 2009/02/17 Multiplicateur de Lagrange Théorème d'inversion de Lagrange Équations de Lagrange Équation différentielle de Lagrange Théorème des quatre carrés de Lagrange Points de Lagrange Formule de Taylor-Lagrange Interpolation lagrangienne Dérivation lagrangienne Points de Lagrange 5

Champ gravitationnel Champ : espace dans lequel l’action d’un système se fait sentir. Champ gravitationnel dû à la présence d'une masse M pouvant exercer une influence gravitationnelle sur tout autre corps présent Il est représenté par un scalaire « potentiel gravitationnel » , potentiel newtonien. Pour une masse m, dans le champ, l’énergie de liaison due à la M est l’énergie potentielle La force subie est : Le potentiel défini par une dérivé est défini à une constante près. Choix : constante nulle = énergie à l’infini nulle (pas de liaison). Les courbes où le potentiel a même valeur s’appellent courbes d’iso potentiel 2009/02/17 Points de Lagrange 6

Les points de Lagrange Un point de Lagrange (noté Li), est une position de l'espace où les champs de gravité de deux corps en orbite l'un autour de l'autre, se combinent de manière à fournir un point d'équilibre à un troisième corps de masse négligeable, tel que les positions relatives des trois corps soient fixes. Forces agissantes • Attraction gravitationnelle des corps • La force centrifuge (inertie rotation) • Force de Coriolis. Une faible masse située exactement en ces points n'en bouge plus. Ce sont les cinq points de Lagrange. 2009/02/17 Points de Lagrange 7

Les points de Lagrange Un peu plus mathématique m Les 5 points de Lagrange : extrema du potentiel gravitationnel d'un système à 2 corps r 1 r 2 r a Potentiel gravitationnel : S G m 1 T m 2 Pulsation : La 3ème loi de Kepler relie la rotation à la distance 2009/02/17 Points de Lagrange 8

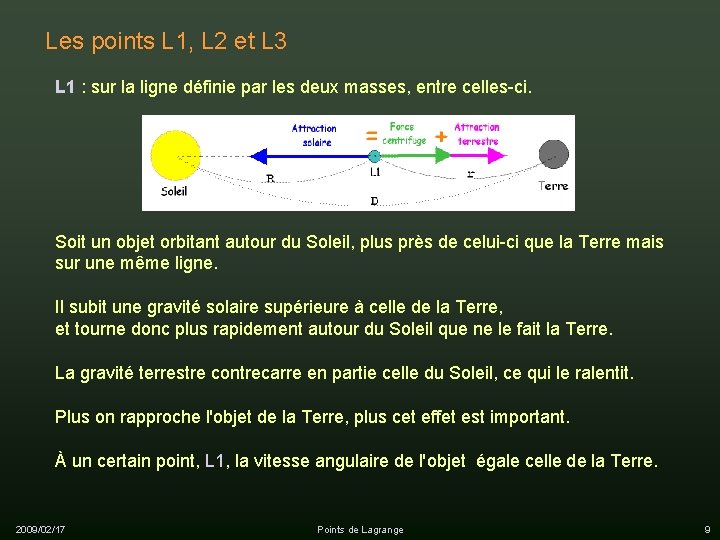
Les points L 1, L 2 et L 3 L 1 : sur la ligne définie par les deux masses, entre celles-ci. Soit un objet orbitant autour du Soleil, plus près de celui-ci que la Terre mais sur une même ligne. Il subit une gravité solaire supérieure à celle de la Terre, et tourne donc plus rapidement autour du Soleil que ne le fait la Terre. La gravité terrestre contrecarre en partie celle du Soleil, ce qui le ralentit. Plus on rapproche l'objet de la Terre, plus cet effet est important. À un certain point, L 1, la vitesse angulaire de l'objet égale celle de la Terre. 2009/02/17 Points de Lagrange 9

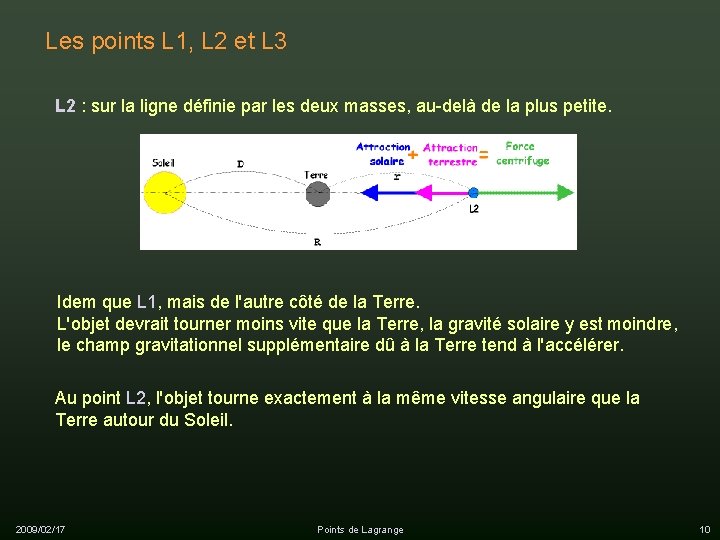
Les points L 1, L 2 et L 3 L 2 : sur la ligne définie par les deux masses, au-delà de la plus petite. Idem que L 1, mais de l'autre côté de la Terre. L'objet devrait tourner moins vite que la Terre, la gravité solaire y est moindre, le champ gravitationnel supplémentaire dû à la Terre tend à l'accélérer. Au point L 2, l'objet tourne exactement à la même vitesse angulaire que la Terre autour du Soleil. 2009/02/17 Points de Lagrange 10

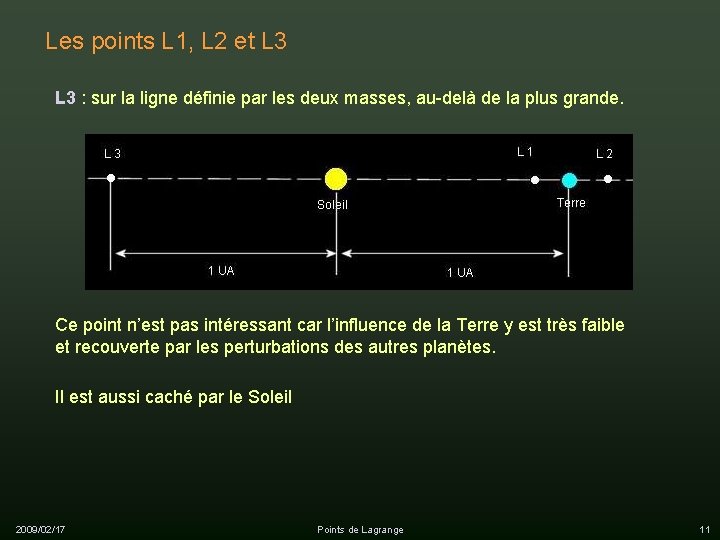
Les points L 1, L 2 et L 3 : sur la ligne définie par les deux masses, au-delà de la plus grande. Ce point n’est pas intéressant car l’influence de la Terre y est très faible et recouverte par les perturbations des autres planètes. Il est aussi caché par le Soleil 2009/02/17 Points de Lagrange 11

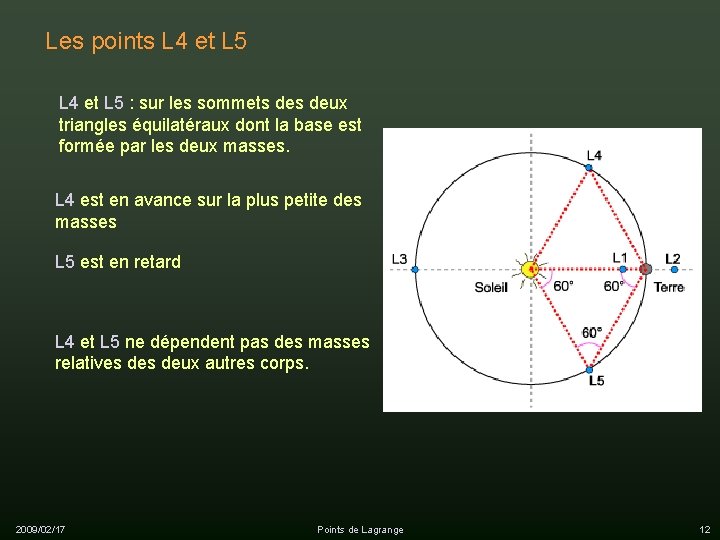
Les points L 4 et L 5 : sur les sommets deux triangles équilatéraux dont la base est formée par les deux masses. L 4 est en avance sur la plus petite des masses L 5 est en retard L 4 et L 5 ne dépendent pas des masses relatives deux autres corps. 2009/02/17 Points de Lagrange 12

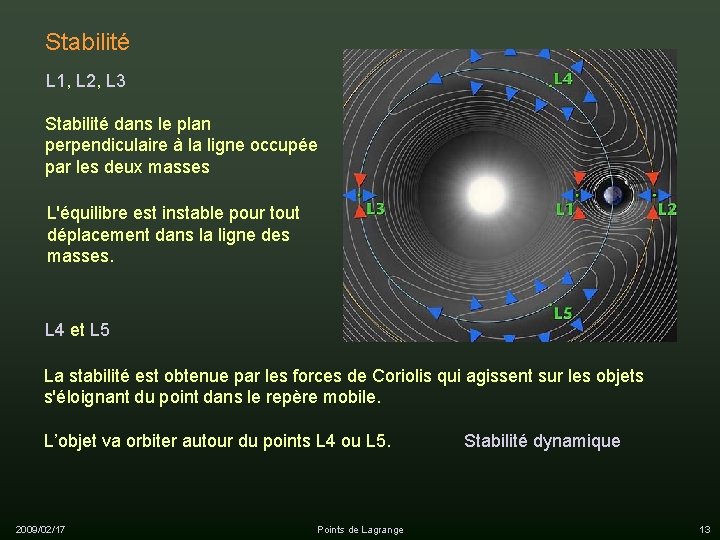
Stabilité L 1, L 2, L 3 Stabilité dans le plan perpendiculaire à la ligne occupée par les deux masses L'équilibre est instable pour tout déplacement dans la ligne des masses. L 4 et L 5 La stabilité est obtenue par les forces de Coriolis qui agissent sur les objets s'éloignant du point dans le repère mobile. L’objet va orbiter autour du points L 4 ou L 5. 2009/02/17 Points de Lagrange Stabilité dynamique 13

La force de Coriolis Force de Coriolis (force fictive ou inertielle) n'existe que parce que l'observateur se trouve dans un référentiel en rotation Aucune force ne s'exerce pour un observateur dans un référentiel galiléen (ou référentiel inertiel). Gaspard-Gustave Coriolis 1792 -1843 1 - observateur immobile La bille se déplace en ligne droite, pas de force en jeu 2 - observateur se déplaçant avec le disque La bille se déplace le long d'un arc de cercle Pseudo-force pour courber la trajectoire : force de Coriolis perpendiculaire à - l'axe de rotation du référentiel - au vecteur vitesse du mouvement Source : wikipédia 2009/02/17 Points de Lagrange 14

Les points de Lagrange – Mythes et réalité Terre - Soleil L 1 Le point de Lagrange L 1 est situé à environ 1 500 000 km de la Terre en direction du Soleil. Anciennes sondes : International Cometary Explorer, Genesis, WIND Sondes actuelles : So. HO, Advanced Composition Explorer Sondes futures : LISA Pathfinder Sondes annulées : Triana L 2 Situé à environ 1 500 000 km de la Terre dans la direction opposée au Soleil. Sondes actuelles : Wilkinson Microwave Anisotropy Probe (WMAP) Sondes futures : James Webb Space Telescope (JWST) Télescope spatial Herschel, Planck, Gaia, Terrestrial Planet Finder, Projet spatial Darwin Sondes annulées : Télescope spatial Eddington 2009/02/17 Points de Lagrange 15

Quelques sondes aux points de Lagrange L 1 et L 2 Soleil Terre L 1 SOHO Observatoire Solaire et Héliospherique Solar and Heliospheric Observatory L 2 WMAP Wilkinson Microwave Anisotropy Probe Mesure les bosses du fond diffus cosmologique 2009/02/17 Points de Lagrange 16

Les points de Lagrange – Mythes et réalité Terre - Soleil L 3 Actuellement, on ne connaît aucun objet situé à cette position. Point de science fiction avec l’Anti Terre. L 4 et L 5 Pas d’objets connus. Terre - Lune L 4 et L 5 Semble abriter des nuages de poussière. Nuages de Kordylewski (Kazimierz) 1960 Vaisseau spatial d’extra terrestres à L 4 ? 2009/02/17 Points de Lagrange 17

Les points de Lagrange – Mythes et réalité Mars - Soleil L 4 - astéroïde 1999 UJ 7 L 5 – astéroïde 5261 Eureka découvert par David Levy en 1990. Astéroïde "Troyen" Jupiter - Soleil L 4 - Astéroïdes troyens (camp grec) L 5 - Astéroïdes troyens (camp troyen) Achille, Patrocle, Hector, Nestor, Priam, Agamemnon, Odyssée… >1690 astéroïdes troyens. Répartition non égale - 696 en L 4 "en avance" Grecs - 519 en L 5 "en retard". Troyens http: //en. wikipedia. org/wiki/List_of_Trojan_asteroids_(Greek_camp) http: //en. wikipedia. org/wiki/List_of_Trojan_asteroids_(Trojan_camp) 2009/02/17 Points de Lagrange 18

Les points de Lagrange – Mythes et réalité Saturne – Dioné (diam. 560 km) L 4 – Hélène (35 km) L 5 – Pollux http: //www. orbitsimulator. com/gravity/ articles/polydeuces. html Saturne –Téthys (diam. 530 km) L 4 - Télesto (30 x 15 km) L 5 - Calypso (30 x 16 km) 2009/02/17 Points de Lagrange 19

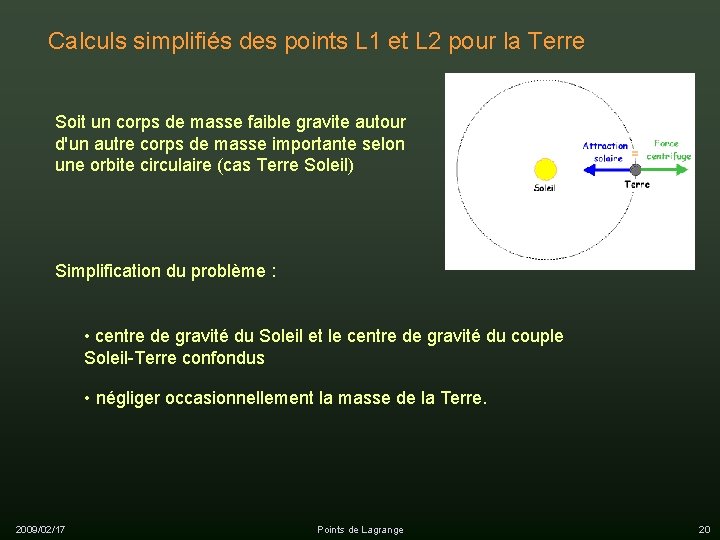
Calculs simplifiés des points L 1 et L 2 pour la Terre Soit un corps de masse faible gravite autour d'un autre corps de masse importante selon une orbite circulaire (cas Terre Soleil) Simplification du problème : • centre de gravité du Soleil et le centre de gravité du couple Soleil-Terre confondus • négliger occasionnellement la masse de la Terre. 2009/02/17 Points de Lagrange 20

Calculs simplifiés des points L 1 et L 2 pour la Terre Equilibre Soleil Terre Equilibre est représenté par l'équation suivante (formule simplifiée) : Force d'attraction du Soleil = Force centrifuge terme (A) = terme (B) G : cte de gravitation universelle M : masse du Soleil m : masse de la Terre D : distance Terre-Soleil en mètres V : vitesse de la Terre en m/s/s Premier terme (A) : force de gravitation ou attraction solaire Second terme (B) : force centrifuge 2009/02/17 Points de Lagrange 21

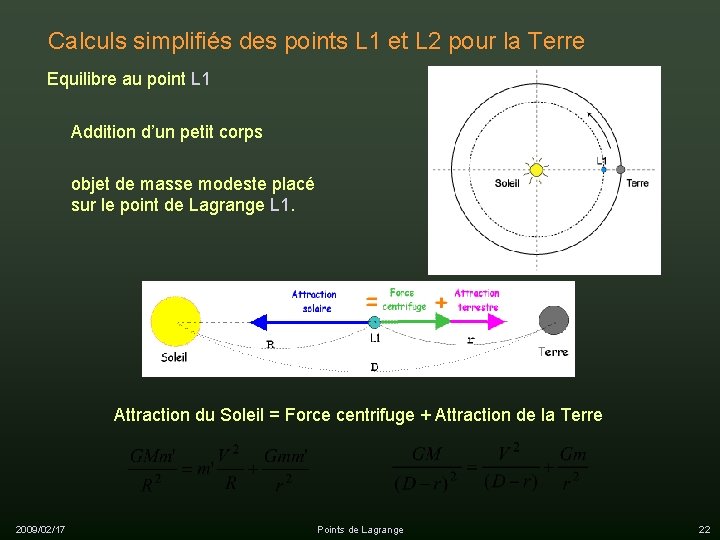
Calculs simplifiés des points L 1 et L 2 pour la Terre Equilibre au point L 1 Addition d’un petit corps objet de masse modeste placé sur le point de Lagrange L 1. Attraction du Soleil = Force centrifuge + Attraction de la Terre 2009/02/17 Points de Lagrange 22

Equilibre au point L 1 Vitesse linéaire Expression de la force centrifuge (1) La période est celle de la Terre : 3ème loi de Kepler : (2) En remplaçant dans (1) 1/P 2 par (2) et en divisant par R = (D-R) 2009/02/17 Points de Lagrange 23

Equilibre au point L 1 Equation d’équilibre : Transformation en divisant par GM ou en prenant x = (r/D) Expression que l’on ne sait pas résoudre analytiquement, mais graphiquement 2009/02/17 Points de Lagrange 24

Equilibre au point L 1 Recherche de la solution de Equation que l’on décompose en deux fonctions m/M = 1/333000 A résoudre sous Géogébra 1 – tracé f(x)-1 2 – tracé g(x)-1=x calculs_l 1 -l 2. ggb Pour simplifier le graphique on soustrait 1 aux deux fonctions 3 – recherche intersection avec un curseur et zoom x = x(P) x 1 = 0. 00997 2009/02/17 r 1 = 1 492 000 km Points de Lagrange 25

Utilisation de calculs_l 1 -l 2. ggb 1 – lancement de Géogébra version 3. 1. 173. 0 2 - Valider la vision de L 1 3 – Faire apparaître f(x) 4 – Faire apparaître g(x) 5 – Faire apparaître la droite verticale mobile avec le point P 1 6 – zoomer et déplacer la droite de façon à la mettre sur l’intersection des deux courbes (pour déplacer le point, cliquer dessus et le faire bouger avec les touches flèches et . 7 – lire son abscisse dans la cellule A 2 8 – la convertir en km. 2009/02/17 Points de Lagrange 26

Equilibre au point L 2 Attraction du Soleil + Attraction de la Terre = Force centrifuge Ici R = (D+r) La formule devient x 2 = 0. 01004 2009/02/17 r 2 = 1 502 000 km Points de Lagrange 27

Equilibre au point L 4 et L 5 La masse du petit corps étant négligeable, le centre de gravité est dur l’axe AB Terre-Lune. Un petit corps en C de masse m’ subit - l’attraction de la Lune - l’attraction de la Terre - la force centrifuge En raccourci, on voit par intuition qu’un triangle équilatéral ABC donnera un équilibre. Le calcul demande quelques notions de trigonométrie et mécanique 2009/02/17 Points de Lagrange 28

Equilibre au point L 4 et L 5 Aperçu graphique par Géogébra On se donne à une distance unité - Un point A de masse M (la Terre) - Un point de masse m (la Lune) - leur centre de gravité D Un petit corps de masse m’ subissant les trois forces. Recherche de la position où la résultante est nulle points_lagrange 2009/02/17 Points de Lagrange 29

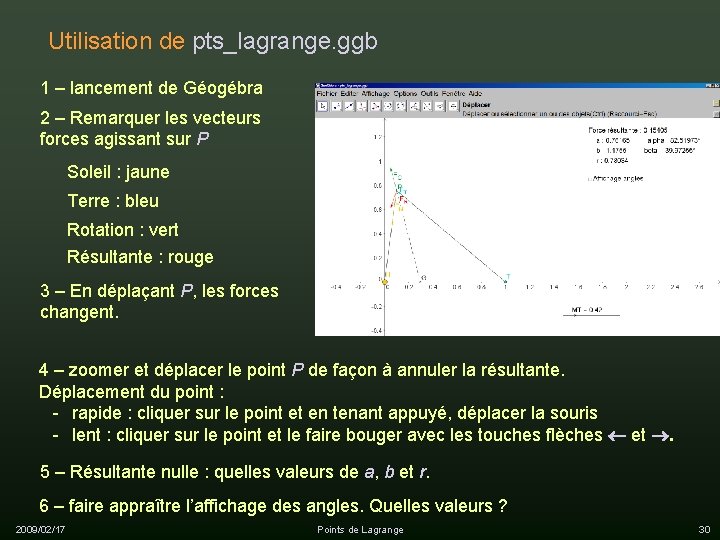
Utilisation de pts_lagrange. ggb 1 – lancement de Géogébra 2 – Remarquer les vecteurs forces agissant sur P Soleil : jaune Terre : bleu Rotation : vert Résultante : rouge 3 – En déplaçant P, les forces changent. 4 – zoomer et déplacer le point P de façon à annuler la résultante. Déplacement du point : - rapide : cliquer sur le point et en tenant appuyé, déplacer la souris - lent : cliquer sur le point et le faire bouger avec les touches flèches et . 5 – Résultante nulle : quelles valeurs de a, b et r. 6 – faire appraître l’affichage des angles. Quelles valeurs ? 2009/02/17 Points de Lagrange 30

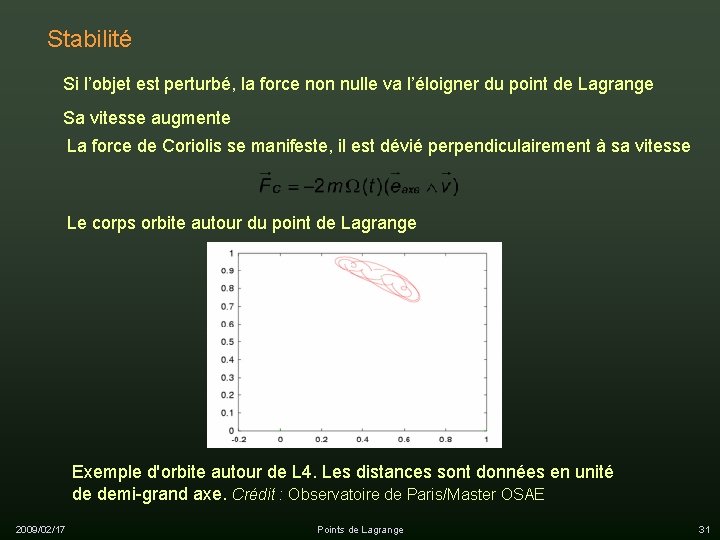
Stabilité Si l’objet est perturbé, la force non nulle va l’éloigner du point de Lagrange Sa vitesse augmente La force de Coriolis se manifeste, il est dévié perpendiculairement à sa vitesse Le corps orbite autour du point de Lagrange Exemple d'orbite autour de L 4. Les distances sont données en unité de demi-grand axe. Crédit : Observatoire de Paris/Master OSAE 2009/02/17 Points de Lagrange 31

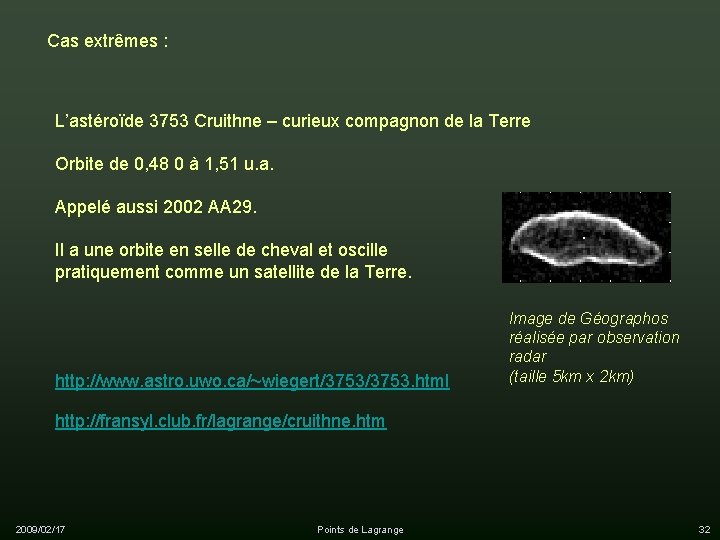
Cas extrêmes : L’astéroïde 3753 Cruithne – curieux compagnon de la Terre Orbite de 0, 48 0 à 1, 51 u. a. Appelé aussi 2002 AA 29. Il a une orbite en selle de cheval et oscille pratiquement comme un satellite de la Terre. http: //www. astro. uwo. ca/~wiegert/3753. html Image de Géographos réalisée par observation radar (taille 5 km x 2 km) http: //fransyl. club. fr/lagrange/cruithne. htm 2009/02/17 Points de Lagrange 32

. . . Fin des petits points 2009/02/17 Points de Lagrange 33