Laboratory and Classroom Study of Low Cycle Fatigue

Laboratory and Classroom Study of Low Cycle Fatigue Rochester Institute of Technology Mechanical Engineering Department Rochester, NY 14623 -5605 M. Kasemer E. A. De. Bartolo S. Boedo American Society of Engineering Education Annual Conference and Exposition Atlanta, GA June 24, 2013 R • I • T Mechanical Engineering

Outline • • • Motivation Course background Activity design Project results Class implementation Summary and future work R • I • T Mechanical Engineering

Motivation • Low Cycle Fatigue (LCF) theory and Fracture Mechanics: important, but often not covered in traditional Mechanical Engineering curriculum – High Cycle Fatigue (HCF) often taught as part of machine element design courses – Static failure theories often taught in strength of materials courses – Flawed assumptions about failure model can have serious consequences. • Some documented efforts to include LCF theory in undergraduate curriculum (Sepahpour and Chang, Hagigat) R • I • T Mechanical Engineering
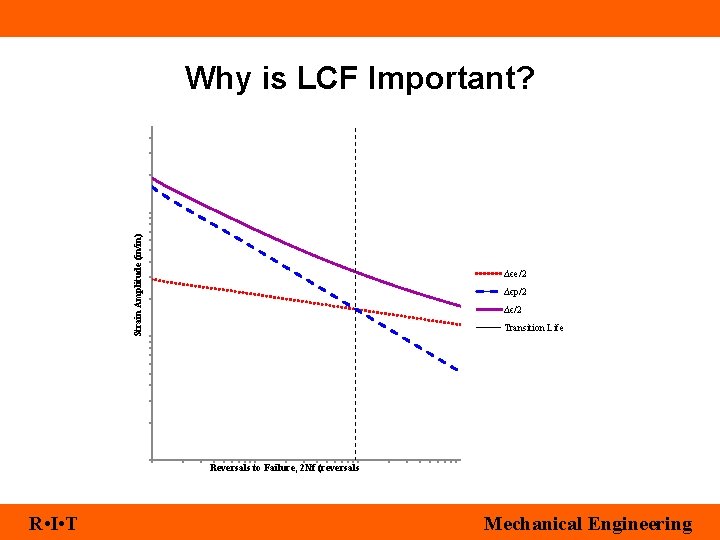
Strain Amplitude (in/in) Why is LCF Important? Δϵe/2 Δϵp/2 Δϵ/2 Transition Life Reversals to Failure, 2 Nf (reversals R • I • T Mechanical Engineering

Why is LCF Important at RIT? • Our students do… – – Work for aircraft industry Work for automotive industry Work in manufacturing Work in biomedical engineering • Our students do not (only)… – Find the factor of safety on infinite life for a rotating shaft with a circular cross-section. R • I • T Mechanical Engineering

RIT Course Background • Design of Machine Elements – – – 10 week (quarter system) course Load and stress analysis (2 weeks) Deflection and stiffness (2 weeks) Static (stress-based) failure theories (1 week) Fatigue (stress-life) (3 weeks) 4 Case studies (throughout quarter, 2 weeks) Note: phasing out machine elements in preparation for conversion to semesters! R • I • T Mechanical Engineering

Case Studies • Added to the course in Fall 2011. • Each involves the design & analysis of a mechanical system. – Examples include the design of cable bar bracket, a bearing test rig, and a microphone stand. • Socratic method: the instructor posed a question, the student provided an answer, followed by another question from the instructor. • Intended to simulate design practice in the workplace or natural cross-disciplinary design team interactions. R • I • T Mechanical Engineering

Course Needs/Constraints • Needs: – Illustrate the limitations of the HCF prediction methods covered in class – Illustrate the importance of understanding the problem at hand before applying a model • Constraints: – Does not add material to an already-full course – Does not require significant additional resources R • I • T Mechanical Engineering

Solution Approach • Student Project: Fatigue and Fracture Mechanics Experiment Design – 5 th year undergraduate student – Create a set of experiments that can be used to show the importance of LCF – Create a set of experiments that can be used to show the importance of fracture mechanics (Bonus student learning through Independent Study!) R • I • T Mechanical Engineering
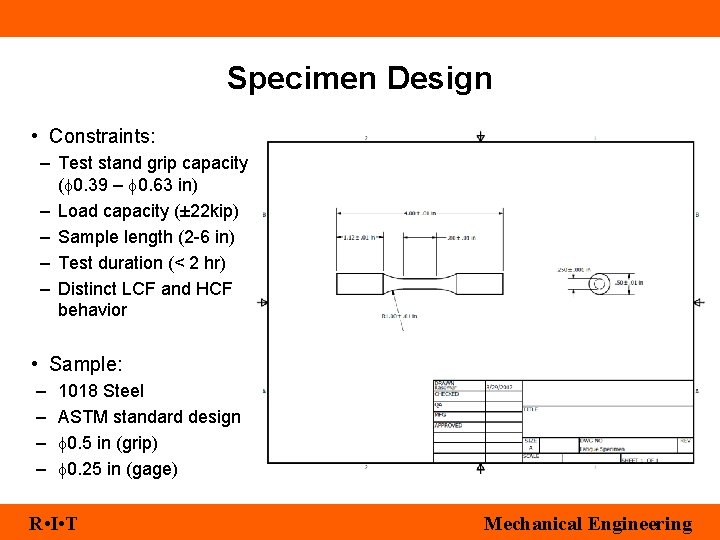
Specimen Design • Constraints: – Test stand grip capacity (f 0. 39 – f 0. 63 in) – Load capacity (± 22 kip) – Sample length (2 -6 in) – Test duration (< 2 hr) – Distinct LCF and HCF behavior • Sample: – – 1018 Steel ASTM standard design f 0. 5 in (grip) f 0. 25 in (gage) R • I • T Mechanical Engineering

Mechanical Characterization • Tensile tests done to determine as-received properties: • • E = 28, 700 ksi Su = 92 ksi Sy = 7 ksi %RA = 40% • Calculated values (Banantine) • • • R • I • T Se’ = 46 ksi and Se = 24. 8 ksi ef’ = 0. 51 sf’ = 142 ksi c = -0. 5 b = -0. 1074 Mechanical Engineering

Test Conditions • Instron 8801 servo-hydraulic fatigue test system • Load control, fully reversed, 10 Hz – Relatively short LCF tests – Manageable HCF tests • 3 HCF tests – Failure expected in > 50 min • 6 LCF tests – Failure expected in < 50 min • Independent Study Results… R • I • T Mechanical Engineering

Fatigue Testing Fatigue test stage Gripped sample Failure is always an option! R • I • T Mechanical Engineering
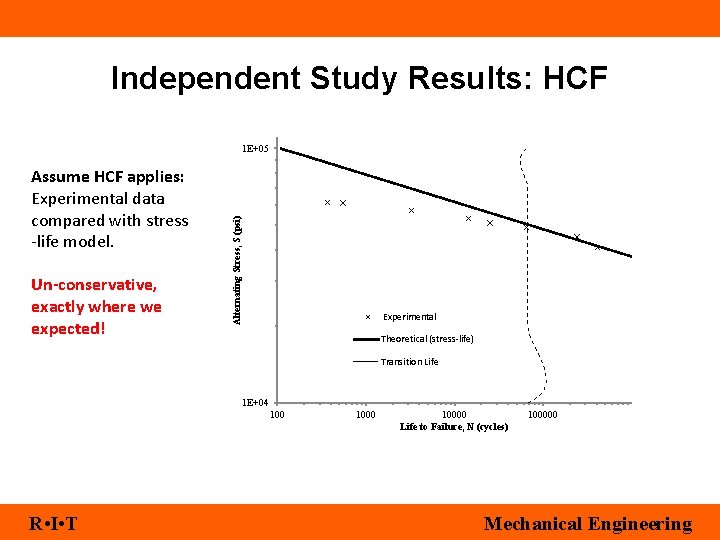
Independent Study Results: HCF Assume HCF applies: Experimental data compared with stress -life model. Un-conservative, exactly where we expected! Alternating Stress, S (psi) 1 E+05 Experimental Theoretical (stress-life) Transition Life 1 E+04 100 R • I • T 10000 Life to Failure, N (cycles) 100000 Mechanical Engineering
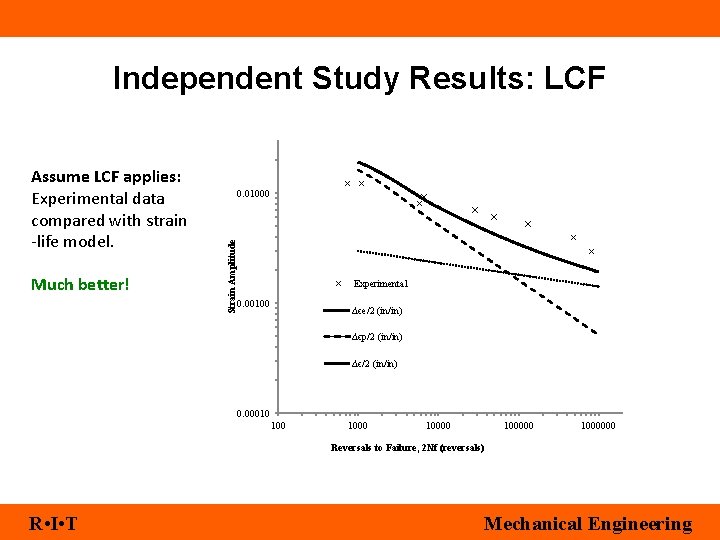
Independent Study Results: LCF Much better! 0. 01000 Strain Amplitude Assume LCF applies: Experimental data compared with strain -life model. Experimental 0. 00100 Δϵe/2 (in/in) Δϵp/2 (in/in) Δϵ/2 (in/in) 0. 00010 100000 1000000 Reversals to Failure, 2 Nf (reversals) R • I • T Mechanical Engineering

Classroom Implementation • Fall 2012 Quarter • LCF problem introduced as a case study • Fatigue tests conducted within 50 minute class period. • Half the class in lecture discussing problem with instructor • Half the class in lab running fatigue tests with TA R • I • T Mechanical Engineering

Classroom Implementation R • I • T Mechanical Engineering
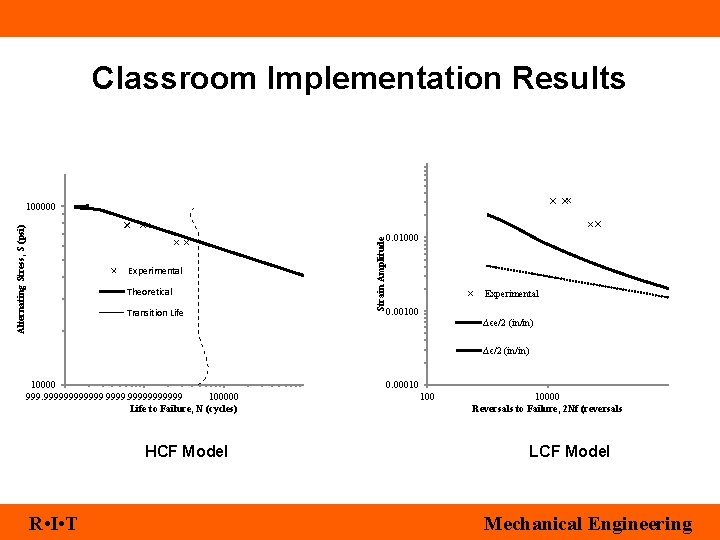
Classroom Implementation Results Experimental Theoretical Transition Life Strain Amplitude Alternating Stress, S (psi) 100000 0. 01000 Experimental 0. 00100 Δϵe/2 (in/in) Δϵ/2 (in/in) 10000 999999 100000 Life to Failure, N (cycles) HCF Model R • I • T 0. 00010 10000 Reversals to Failure, 2 Nf (reversals LCF Model Mechanical Engineering

“What? !? ” R • I • T Mechanical Engineering

“It’s not a mistake, it’s a learning experience” • Reviewed all data, back to tensile test to characterize material • • R • I • T 1065 steel ordered, not 1018 E = 70, 000 ksi Su = 129 ksi (published: 92. 1 ksi) %RA = 40% (published: 45%) Mechanical Engineering

“It’s not a mistake, it’s a learning experience” • Reviewed all data, back to tensile test to characterize material • • 1065 steel ordered, not 1018 E = 70, 000 ksi Su = 129 ksi (published: 92. 1 ksi) %RA = 40% (published: 45%) • Likely problems with data collection • Test frame down during following quarter for repairs, so no opportunity to investigate R • I • T Mechanical Engineering

Results from Fall 2012 Class Infinite Life problem (p=0. 348) Number of students Mean score (max 25) Standard deviation Finite Life problem (p=0. 000002) Number of students Mean score (max 25) Standard deviation Fall 2011 42 21. 79 2. 97 Fall 2011 42 22. 24 3. 47 Fall 2012 34 21. 21 2. 23 Fall 2012 34 18. 00 3. 73 “Was the addition of the fatigue test as a course topic a positive change? ” Yes: 21 No: 6 Did not answer: 7 R • I • T Mechanical Engineering

Summary and Future Work • Suspect data: interesting discussion, but may have led to confusion about the activity goal • Select different materials in future: • 1018 steel (as called for) • Al alloy (to illustrate endurance limit issues) • Exam questions to measure lab outcome will be more carefully chosen – focus on LCF/HCF distinction R • I • T Mechanical Engineering

Acknowledgements Steel stock was purchased and samples were machined by the RIT Machine shop staff. Their help is much appreciated! References 1. 2. 3. R • I • T Sepahpour, B. , and Chang, S. -R. , 2005, “Low Cycle and Finite Life Fatigue Experiment, ” Proceedings of the 2005 ASEE Annual Conference and Exposition, ASEE. Hagigat, C. K. , 2005, “Using Commercially Available Finite Element Software for Fatigue Analysis, ” Proceedings of the 2005 ASEE Annual Conference and Exposition, ASEE. Bannantine, J. A. , Comer, J. J. , and Handrock, J. L. , 1990, Fundamentals of Metal Fatigue Analysis, Prentice Hall, Englewood Cliffs, NY. Mechanical Engineering

R • I • T Mechanical Engineering
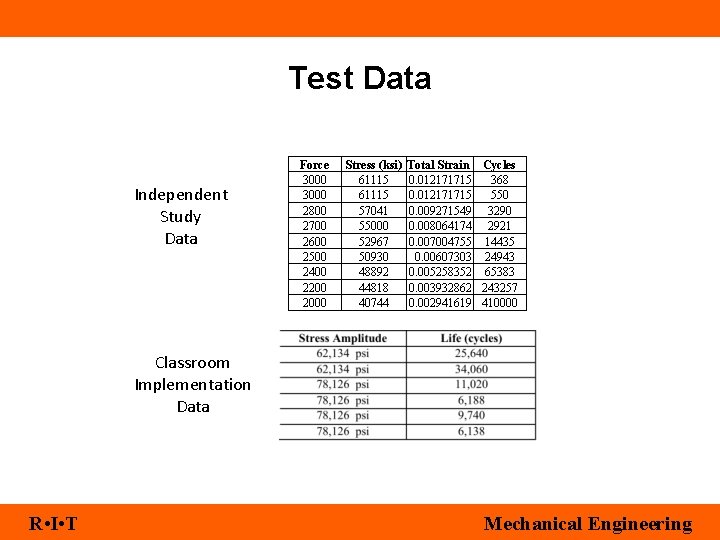
Test Data Independent Study Data Force 3000 2800 2700 2600 2500 2400 2200 2000 Stress (ksi) 61115 57041 55000 52967 50930 48892 44818 40744 Total Strain Cycles 0. 012171715 368 0. 012171715 550 0. 009271549 3290 0. 008064174 2921 0. 007004755 14435 0. 00607303 24943 0. 005258352 65383 0. 003932862 243257 0. 002941619 410000 Classroom Implementation Data R • I • T Mechanical Engineering

Fracture Mechanics Experiment Three “crack” (sharp notch) configurations on one sample: Center crack, 2 a Single edge crack, 2 a Double edge crack, a & a Which will fail first…? R • I • T Mechanical Engineering
- Slides: 27