Lab descriptions Lab Pitch tuner Lab Self balancing

Lab descriptions • Lab: Pitch tuner • Lab: Self balancing platform Labs: pitch tuner and self balancing platform (v. 5 b) 1

Laboratory 1 A simple Pitch tuner Labs: pitch tuner and self balancing platform (v. 5 b) 2

Objectives • To lean how to interface analogue signals to digital systems • To learn how to process audio signals in embedded systems. • Aim • To develop a pitch tuner using an embedded system. Labs: pitch tuner and self balancing platform (v. 5 b) 3

Signal processing steps • • Capture signal by microphone Amplify the signal Feed to ADC of AMR 7 micro. Convert to digital , find autocorrelation coeff. • Find pitch Labs: pitch tuner and self balancing platform (v. 5 b) 4

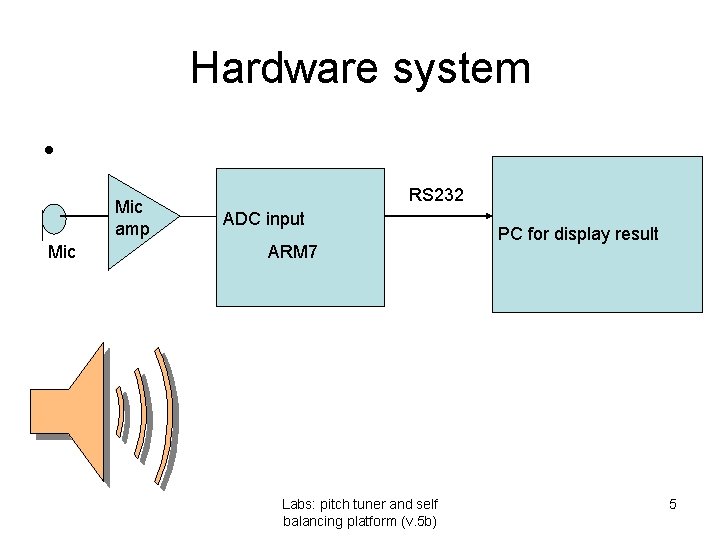
Hardware system • Mic amp Mic RS 232 ADC input ARM 7 Labs: pitch tuner and self balancing platform (v. 5 b) PC for display result 5

Amplifier What is the best bias voltage at pin 3(non-invert. input) ? • • Condenser MIC output impedance is 75 Ohms, why this circuit is not a good design. How to correct it? – Hint: Input=1 KHZ, find impedance of C 1 and input of the amp. – Solution: C 1>1 u. F, R 2=1 K, V 3 = 100 K(VR), use , one VR to replace VR 1, 2. Discuss why? Labs: pitch tuner and self balancing platform (v. 5 b) 6

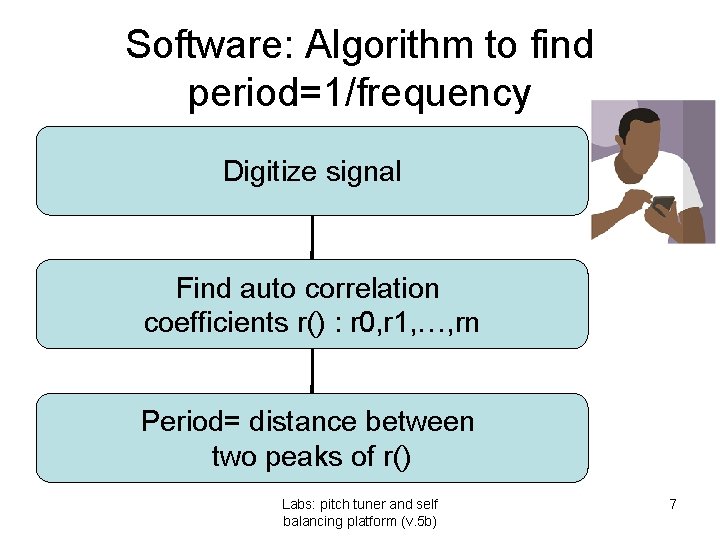
Software: Algorithm to find period=1/frequency Digitize signal Find auto correlation coefficients r() : r 0, r 1, …, rn Period= distance between two peaks of r() Labs: pitch tuner and self balancing platform (v. 5 b) 7

Pitch Estimation Method : ACF (Autocorrelation function) • Autocorrelation function (ACF) x n R m Labs: pitch tuner and self balancing platform (v. 5 b) n Symmetrical on both side 8

What is Autocorrelation, R(m)? • • • E. g. x=[1 5 7 1 4 ] N=5, R(0)=[x(0)*x(0)+x(1)*x(1)+x(2)*x 2+x(3)*x(3)+x(4)*x(4)] R(0)= (1+ 25+49+1+16)=92 • • • R(1)=[x(0)*x(1)+x(1)*x(2)+x(2)*x(3)+x(3)*x(4)] x=[1 5 7 1 4 ] (5+ 35+ 7+ 4)=51 And so on… R=[92. 0000 51. 0000 40. 0000 21. 0000 4. 0000] • Labs: pitch tuner and self balancing platform (v. 5 b) 9

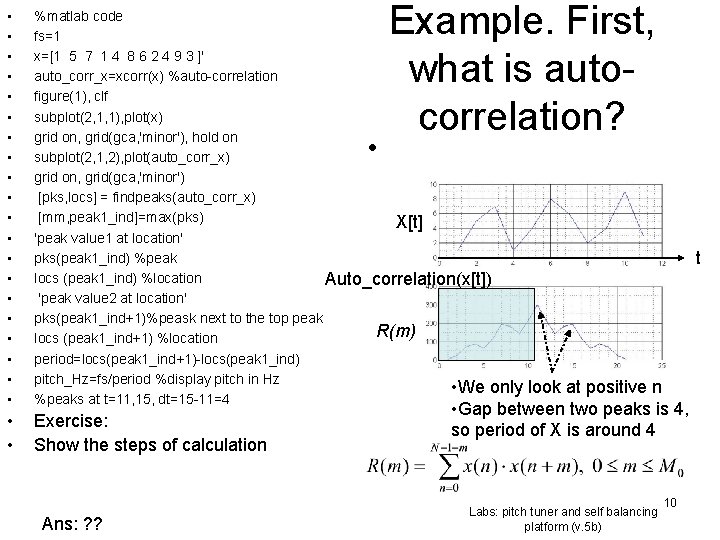
Example. First, what is autocorrelation? • • • • • %matlab code fs=1 x=[1 5 7 1 4 8 6 2 4 9 3 ]' auto_corr_x=xcorr(x) %auto-correlation figure(1), clf subplot(2, 1, 1), plot(x) grid on, grid(gca, 'minor'), hold on subplot(2, 1, 2), plot(auto_corr_x) grid on, grid(gca, 'minor') [pks, locs] = findpeaks(auto_corr_x) [mm, peak 1_ind]=max(pks) X[t] 'peak value 1 at location' pks(peak 1_ind) %peak locs (peak 1_ind) %location Auto_correlation(x[t]) 'peak value 2 at location' pks(peak 1_ind+1)%peask next to the top peak R(m) locs (peak 1_ind+1) %location period=locs(peak 1_ind+1)-locs(peak 1_ind) pitch_Hz=fs/period %display pitch in Hz • We only %peaks at t=11, 15, dt=15 -11=4 • • Exercise: Show the steps of calculation • Ans: ? ? t look at positive n • Gap between two peaks is 4, so period of X is around 4 Labs: pitch tuner and self balancing platform (v. 5 b) 10

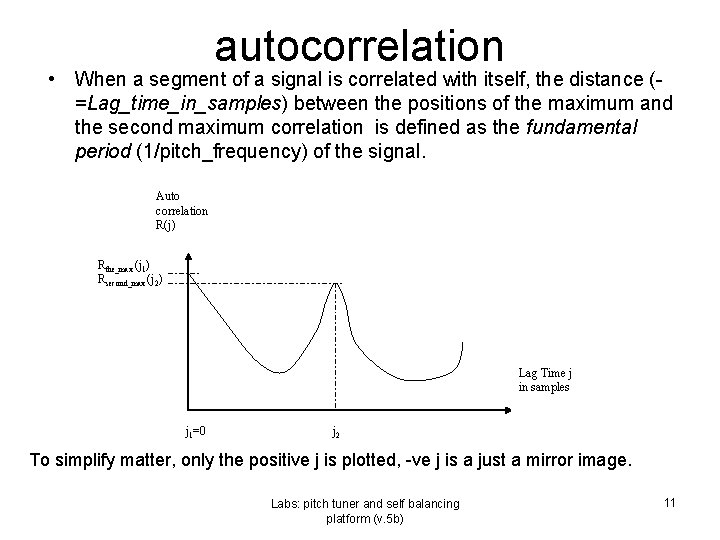
autocorrelation • When a segment of a signal is correlated with itself, the distance (=Lag_time_in_samples) between the positions of the maximum and the second maximum correlation is defined as the fundamental period (1/pitch_frequency) of the signal. Auto correlation R(j) Rthe_max (j 1) Rsecond_max (j 2) Lag Time j in samples j 1=0 j 2 To simplify matter, only the positive j is plotted, -ve j is a just a mirror image. Labs: pitch tuner and self balancing platform (v. 5 b) 11

Then the fundamental frequency can be calculated as: • Usually assume j 1=0, then Labs: pitch tuner and self balancing platform (v. 5 b) 12

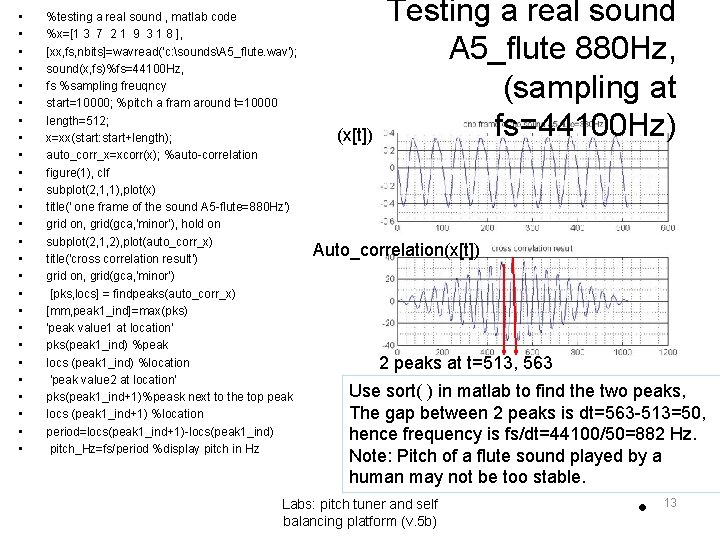
• • • • • • • %testing a real sound , matlab code %x=[1 3 7 2 1 9 3 1 8 ], [xx, fs, nbits]=wavread('c: soundsA 5_flute. wav'); sound(x, fs)%fs=44100 Hz, fs %sampling freuqncy start=10000; %pitch a fram around t=10000 length=512; x=xx(start: start+length); auto_corr_x=xcorr(x); %auto-correlation figure(1), clf subplot(2, 1, 1), plot(x) title(' one frame of the sound A 5 -flute=880 Hz') grid on, grid(gca, 'minor'), hold on subplot(2, 1, 2), plot(auto_corr_x) title('cross correlation result') grid on, grid(gca, 'minor') [pks, locs] = findpeaks(auto_corr_x) [mm, peak 1_ind]=max(pks) 'peak value 1 at location' pks(peak 1_ind) %peak locs (peak 1_ind) %location 'peak value 2 at location' pks(peak 1_ind+1)%peask next to the top peak locs (peak 1_ind+1) %location period=locs(peak 1_ind+1)-locs(peak 1_ind) pitch_Hz=fs/period %display pitch in Hz (x[t]) Testing a real sound A 5_flute 880 Hz, (sampling at fs=44100 Hz) Auto_correlation(x[t]) 2 peaks at t=513, 563 Use sort( ) in matlab to find the two peaks, The gap between 2 peaks is dt=563 -513=50, hence frequency is fs/dt=44100/50=882 Hz. Note: Pitch of a flute sound played by a human may not be too stable. Labs: pitch tuner and self balancing platform (v. 5 b) • 13

Matlab example 1 • • a=[1 3 9 3 2 3 8 3 2 ], r=(xcorr(a)) , round (r) R=r(j=time lag) r=[ 2 9 35 60 96 123 86 72 96 60 72 86 123 190 35 9 17 2] • Exercise • Verify by hand the first 3 (r [ j ]) elements after the signal overlapped with itself. Labs: pitch tuner and self balancing platform (v. 5 b) 14

Matlab Example 2: a=[1 3 9 3 2 3 8 3 2 ], r=(xcorr(a)) figure(1), clf, subplot(2, 1, 1) plot(a), subplot(2, 1, 2)plot(r) Data (a) Auto Corr. Xcorr (r) Pick 2 peaks and measure period Period=4, The middle is the peak Labs: pitch tuner and self balancing platform (v. 5 b) 15

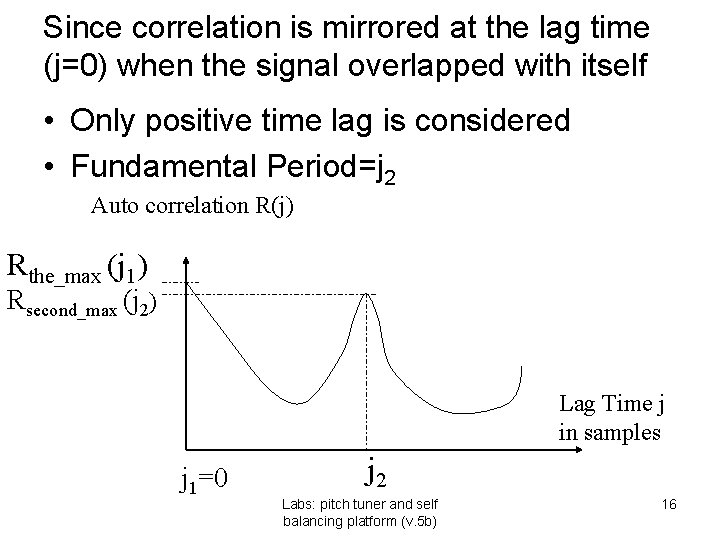
Since correlation is mirrored at the lag time (j=0) when the signal overlapped with itself • Only positive time lag is considered • Fundamental Period=j 2 Auto correlation R(j) Rthe_max (j 1) Rsecond_max (j 2) Lag Time j in samples j 1=0 j 2 Labs: pitch tuner and self balancing platform (v. 5 b) 16

Matlab Example 3: y=sin wave of 440 Hz • • • dt=0. 0001 time=[0: dt: 2] freq=440 nu=2. 0*pi*freq y=sin(nu*time) %angular freq. (sin wave of 440 Hz) r=(xcorr(y)) figure(2) , clf, subplot(2, 1, 1), plot(time, y) axis ([0 0. 01 -1 1]) subplot(2, 1, 2), plot(time(1: 100), r(1: 100)) Labs: pitch tuner and self balancing platform (v. 5 b) 17

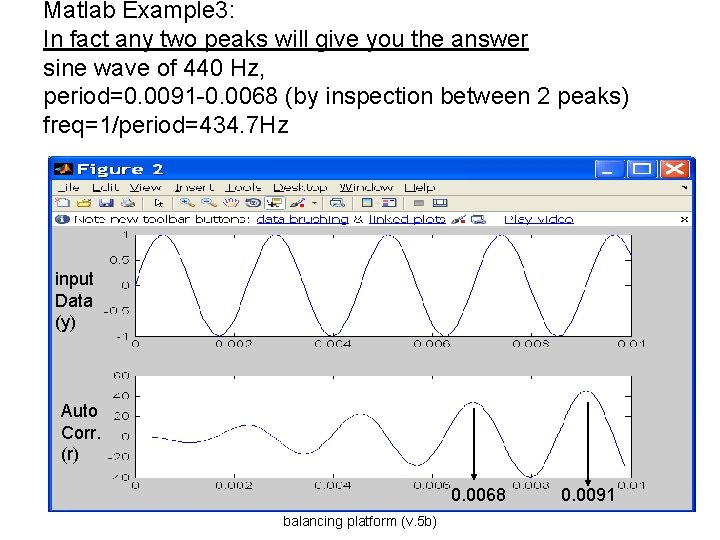
Matlab Example 3: In fact any two peaks will give you the answer sine wave of 440 Hz, period=0. 0091 -0. 0068 (by inspection between 2 peaks) freq=1/period=434. 7 Hz input Data (y) Auto Corr. (r) Labs: pitch tuner and self balancing platform (v. 5 b) 0. 0068 0. 0091 18

Conclusion • Studied a method of measuring the pitch of an audio sound. Labs: pitch tuner and self balancing platform (v. 5 b) 19

Laboratory 2 A self balancing platform Labs: pitch tuner and self balancing platform (v. 5 b) 20

Objectives • 1. Objectives – To lean how to interface a direct current (DC) output sensor to an microcontroller – To learn how to implement a Proportional–Integral– Derivative PID feed back control system. • 2. Aim – To develop a self-balancing platform using an embedded system. • Reference: http: //www. cse. cuhk. edu. hk/%7 Ekhwong/ceg 3480/PID_DC_motor_Control 08. ppt Labs: pitch tuner and self balancing platform (v. 5 b) 21

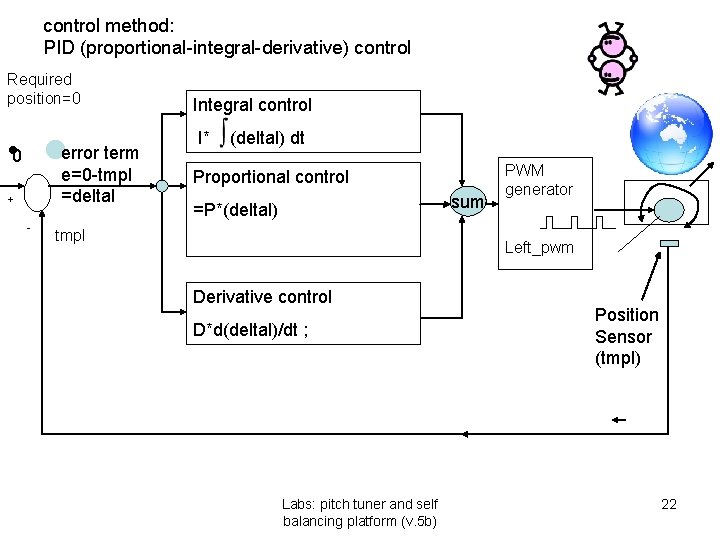
control method: PID (proportional-integral-derivative) control Required position=0 • 0 lerror term e=0 -tmpl =deltal + - Integral control I* (deltal) dt Proportional control sum =P*(deltal) tmpl PWM generator Left_pwm Derivative control D*d(deltal)/dt ; Labs: pitch tuner and self balancing platform (v. 5 b) Position Sensor (tmpl) 22

The experimental setup • video Labs: pitch tuner and self balancing platform (v. 5 b) 23

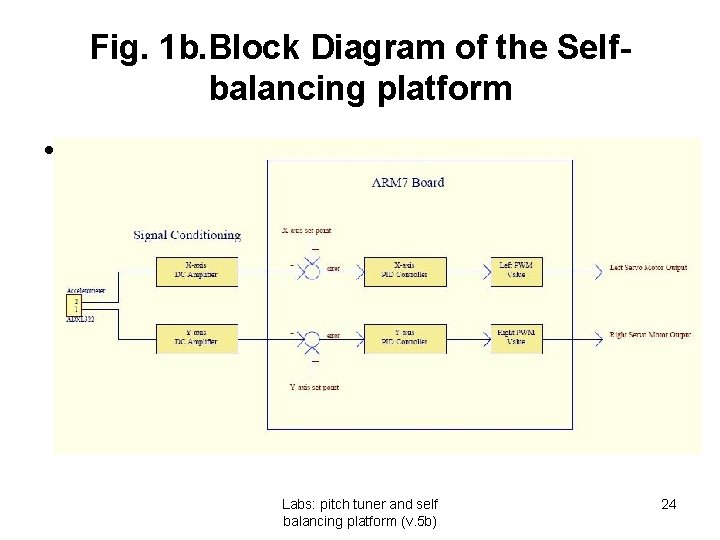
Fig. 1 b. Block Diagram of the Selfbalancing platform • Labs: pitch tuner and self balancing platform (v. 5 b) 24

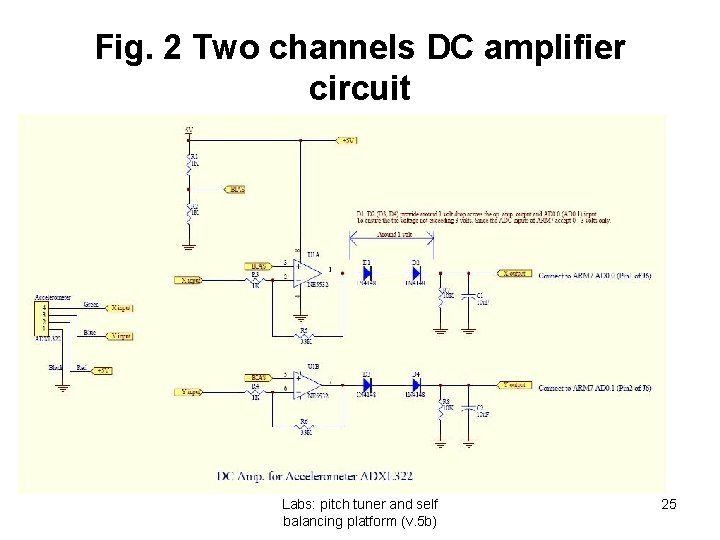
Fig. 2 Two channels DC amplifier circuit • Labs: pitch tuner and self balancing platform (v. 5 b) 25

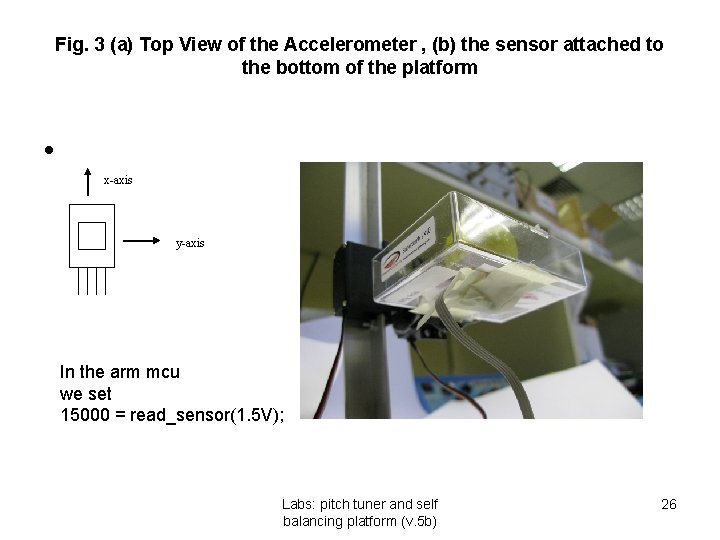
Fig. 3 (a) Top View of the Accelerometer , (b) the sensor attached to the bottom of the platform • x-axis y-axis In the arm mcu we set 15000 = read_sensor(1. 5 V); Labs: pitch tuner and self balancing platform (v. 5 b) 26

Special techniques • MIDL is the mid set point value for X-axis • Use integer “int” to simulate floating point – Multiply the value by x and divide it by x afterwards, (e. g. x=200 in our example) – tmpl is the tilt position measurement • e=deltal = (tmpl - (MIDL+200)) / 200; • Derivative is d[e(t)] / dt = e (current ) – e (previous) – diffl = deltal – lastl; • Integration is e dt = e (current) + e (previous) • accul += deltal/200; //arbitrary set to divide by 200, Dead-band (see next page) Labs: pitch tuner and self balancing platform (v. 5 b) 27

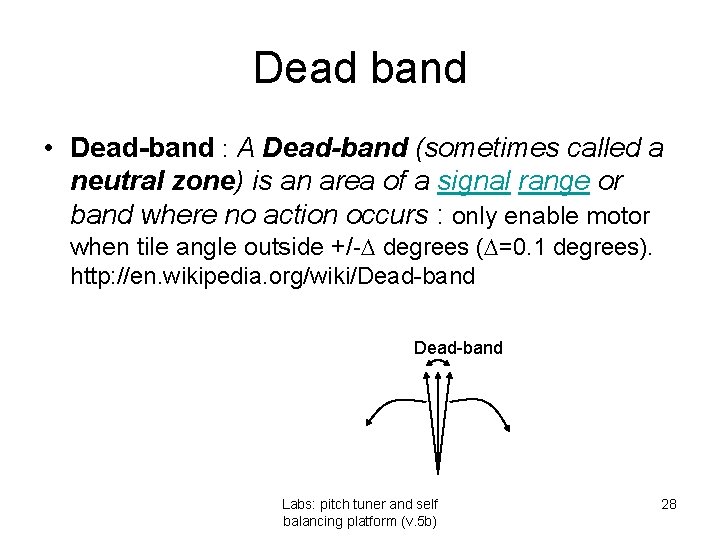
Dead band • Dead-band : A Dead-band (sometimes called a neutral zone) is an area of a signal range or band where no action occurs : only enable motor when tile angle outside +/- degrees ( =0. 1 degrees). http: //en. wikipedia. org/wiki/Dead-band Labs: pitch tuner and self balancing platform (v. 5 b) 28

Algorithm of left motor (core loop in timer IRQ_exception) 500 Hz • • void __irq IRQ_Exception() { – • • • • • • • • tmpl = read_sensor(0); // read X-axis value //putint(tmpl); // print("; "); if (tmpl>=(MIDL+200)) { deltal = (tmpl - (MIDL+200))/200; diffl = deltal-lastl; if(diffl<maxdiff) { // display on terminal // if X-axis value >= setpoint plus 200 // calculate the error and normalize it // caculate the different between current and last error // ignore if the error different > max. difference // this prevent the noise due to undesired movement of accelerometer lastl = deltal; // save error as the last error left. PWM = left. PWM - (P*deltal - I*accul + D*diffl); // update the left PWM value by PID if (left. PWM<MINOUTPUT) left. PWM = MINOUTPUT; // limit the PWM value to its minimum if(accul<maxaccu) accul += deltal/200; // ensure the integral not exceed the maximum PWMMR 2=left. PWM; // set the left PWM output PWMLER = 0 x 24; //enable match 2, 5 latch to effective } } else if (tmpl<=(MIDL-200)) { // if X-axis value <= setpoint plus 200 deltal = ((MIDL-200) - tmpl)/200; // calculate the error and normalize it diffl = deltal- lastl; // caculate the different between current and last error if(diffl<maxdiff) { // ignore if the error different > max. difference // this prevent the noise due to undesired movement of accelerometer lastl = deltal; // save error to the last error left. PWM = left. PWM + P*deltal + I*accul + D*diffl; if (left. PWM>MAXOUTPUT) left. PWM = MAXOUTPUT; if(accul>0) accul -= deltal/100; // ensure the integral not less than zero PWMMR 2=left. PWM; // set the left PWM output PWMLER = 0 x 24; } } ////////////////////////// // update the left PWM value by PID // limit the PWM value to its maximum //enable match 2, 5 latch to effective Labs: pitch tuner and self balancing platform (v. 5 b) 29

if (tmpl>=(MIDL+200)) Tile position > degrees (outside dead band) • void __irq IRQ_Exception() //running at 500 Hz, set by timer • { tmpl = read_sensor(0); // read X-axis value //putint(tmpl); • if (tmpl>=(MIDL+200)) {// if X-axis value >= setpoint plus 200 • deltal = (tmpl - (MIDL+200))/200; // cal. error and normalize it • diffl = deltal-lastl; // cal. different between current and last error • if(diffl<maxdiff) // ignore if the error different > max. difference • {//prevents noise from undesired accelerometer movement lastl = deltal; // save error as the last error • left. PWM = left. PWM - (P*deltal - I*accul +D*diffl); //update. PWM • if (left. PWM<MINOUTPUT) • left. PWM = MINOUTPUT; // limit PWM to its min. • if(accul<maxaccu) //make sure accul cannot grow too big • accul += deltal/200; • // ensure integral< maximum • PWMMR 2=left. PWM; // set the left PWM output • PWMLER = 0 x 24; //enable match 2, 5 latch to effective • } Labs: pitch tuner and self 30 • } balancing platform (v. 5 b)

Else of if (tmpl>=(MIDL+200)) Tile position <= degrees (outside dead band) • else if (tmpl<=(MIDL-200)) • { Similar but the rotation is reversed • }////////////////////////// Labs: pitch tuner and self balancing platform (v. 5 b) 31

Question 1) Is the output voltage changes linearly with the tilt angle? 2) What is the effect on the performance of the system when the sampling frequency is 100 Hz? 3) The deadband in sensor reading is +/-200. Estimate the deadband in degrees of our system. 4) What is the effect on the performance of the system when the sampling frequency is 1000 Hz? Explain your observation. Labs: pitch tuner and self balancing platform (v. 5 b) 32

Conclusion • Studied how to interface direct currents sensor to a embedded system • Studied how to build and tune a PID control system Labs: pitch tuner and self balancing platform (v. 5 b) 33