Lab Demo 1 Dr Mai Elshehaly What is

Lab Demo 1 Dr. Mai Elshehaly

What is Python? • An interpreted language • Executes instructions directly, without previously compiling a program into machine-language instructions

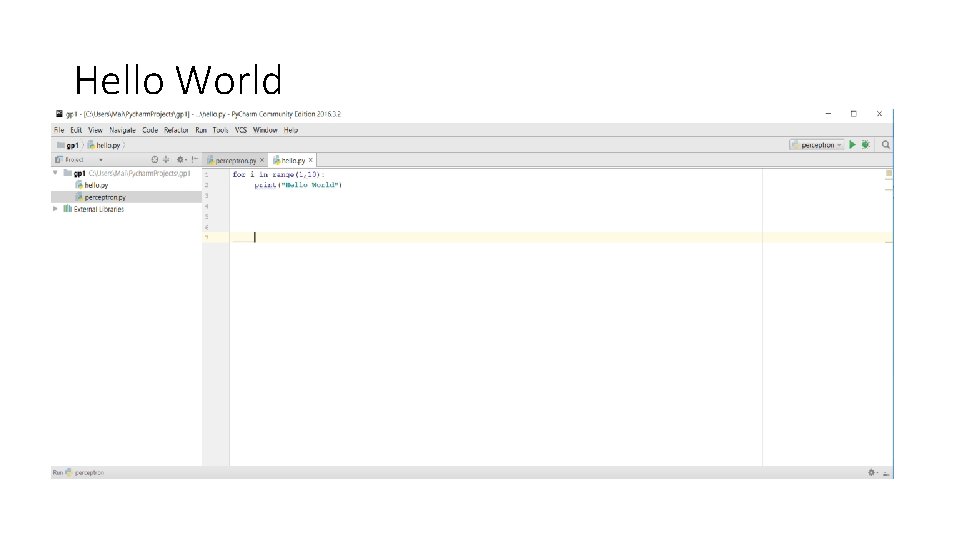
Hello World

Indentation acts as {}

Classes in Python • A class is a way to group variables and functions that work together to define a certain functionality in your code. • Let’s say we want to write code to simulate a dog • We will create a class named “Dog” • Let’s do this!

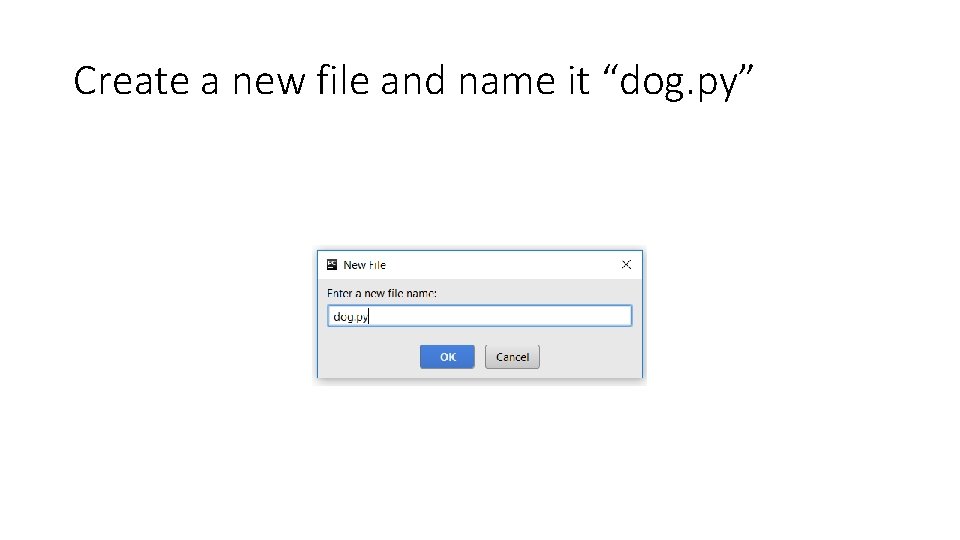
Create a new file and name it “dog. py”

Class definition

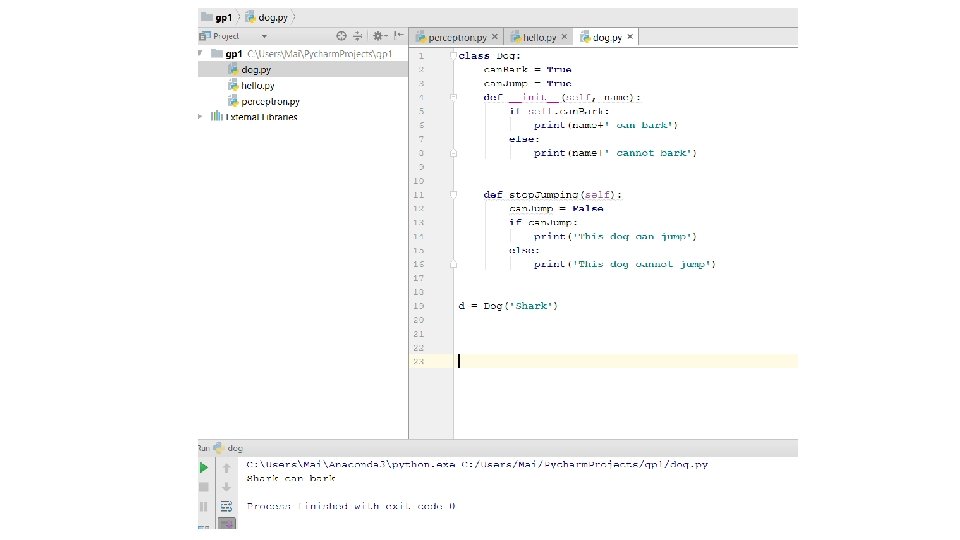
Run your code. Nothing happens! Why? • What we wrote so far is a class definition • This is equivalent to saying: Hypothetically if there is any dog in the street, we assume that it can bark, and it can jump. • This doesn’t mean we’re talking about a specific dog • So we haven’t actually seen a real dog • We only know what dogs in general can do

Now let’s instantiate our class • Meaning: we will create an object which is an instance of the class Dog • This will mean a specific dog • Now we can execute some of his actions (functions) and/or read his properties

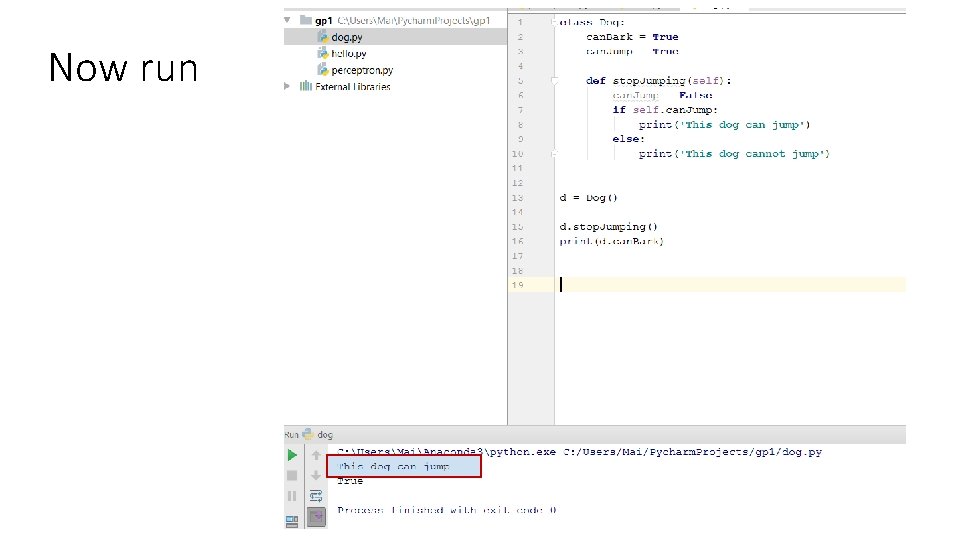
Now run

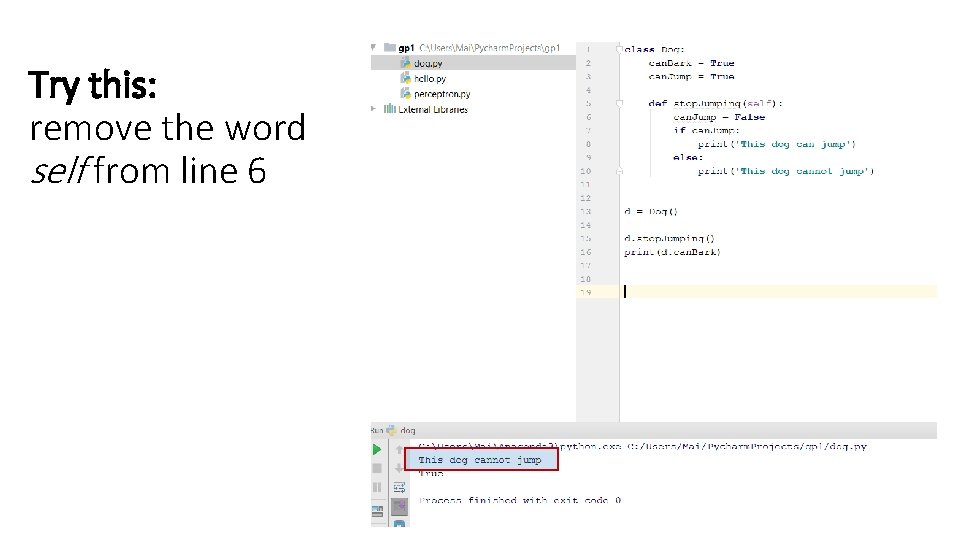
Try this: remove the word self from line 6

What happened? • We defined the variable can. Jump twice • The first is a member of the class definition, we can refer to it using the keyword self • The second is local

The __init__ function • Notice how we had to call the stop. Jumpint() method in our code • Nothing happened when we instantiated the class because the class has no entry point • The __init__ function is a special function we define for our class • It gets executed as soon as an object is created

What we learned so far: • How to define a class • How to create initialization code in __init__ function • How to create an object to instantiate the class • How to call member functions of a class

Create a new file: data. Maker. py

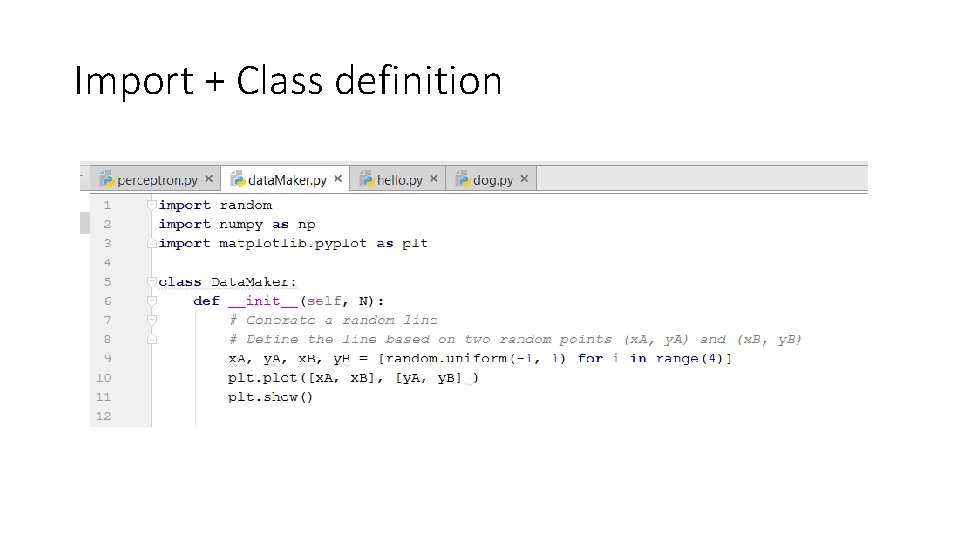
Import + Class definition

Instantiate and run (multiple times)

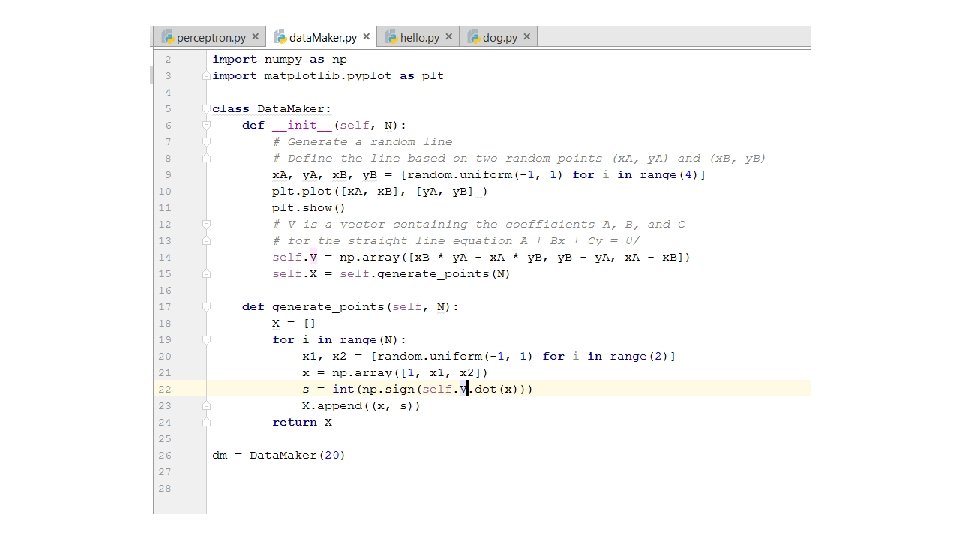
Refresher: Equation of a line passing through 2 points A + Bx + Cy = 0 Where, A = x. B*y. A – x. A*y. B B = y. B – y. A C = x. A – x. B

Generate points on both sides of the line • Define a vector V of coefficients for the line equation • Calculate new points X by using dot product • For any point on the line: x. V = 0 • For any point below the line: x. V is negative • For any point above the line: x. V is positive