Lab 6 Geometric Transformations Matrix Type in Open

Lab 6 Geometric Transformations

�Matrix Type in Open. GL gl. Matrix. Mode(mode) mode : The matrix stack that is the target for subsequent matrix operations. The mode parameter can assume one of three values. �GL_MODELVIEW ->Modeling , Viewing �GL_PROJECTION ->Projection �GL_TEXTURE �Use this function when draw, Translation , Rotation , Scaling �gl. Translate*() �gl. Rotate*() �gl. Scale*() �glut. Look. At()

�Although the gl. Matrix. Mode does not used when drawing the shape or Rotate it in Some programs but they are true. Why? Because the MODELVIEW is the default matrix. �Void gl. Load. Identity(void); Used to reset a matrix , Should be always use after gl. Matrix. Mode(mode)

�gl. Matrix. Mode(mode) When use GL_PROJECTION or GL_TEXTURE or. GL_COLOR We must use GL_MODELVIEW �Example: gl. Matrix. Mode(GL_PROJECTION); gl. Load. Identity(); glu. Ortho 2 D(45. 0, (… , … , …); gl. Matrix. Mode(GL_MODELVIEW); gl. Load. Identity();

�There is a stack of matrices for each of the matrix modes. In GL_MODELVIEW mode, the stack depth is at least 32. In the other two modes, GL_PROJECTION and GL_TEXTURE, the depth is at least 2. The current matrix in any mode is the matrix on the top of the stack for that mode.

�Void gl. Push. Matrix(void); Save model-view matrix setting �Void gl. Pop. Matrix(void); Restore the model-view matrix

�The gl. Push. Matrix function pushes the current matrix stack down by one, duplicating the current matrix. That is, after a gl. Push. Matrix call, the matrix on the top of the stack is identical to the one below it. �The gl. Pop. Matrixfunction pops the current matrix stack, replacing the current matrix with the one below it on the stack. Initially, each of the stacks contains one matrix, an identity matrix.

1. 2. 3. Translation Rotation Scaling

The gl. Translate* function multiplies the current matrix by a translation matrix. float gl. Translatef(Glfloat x , Glfloat y , Glfloat z); Double gl. Translated(Gldouble x, Gldouble y, Gldouble z); Displacement on �X: x axis �Y: y axis �Z: z axis
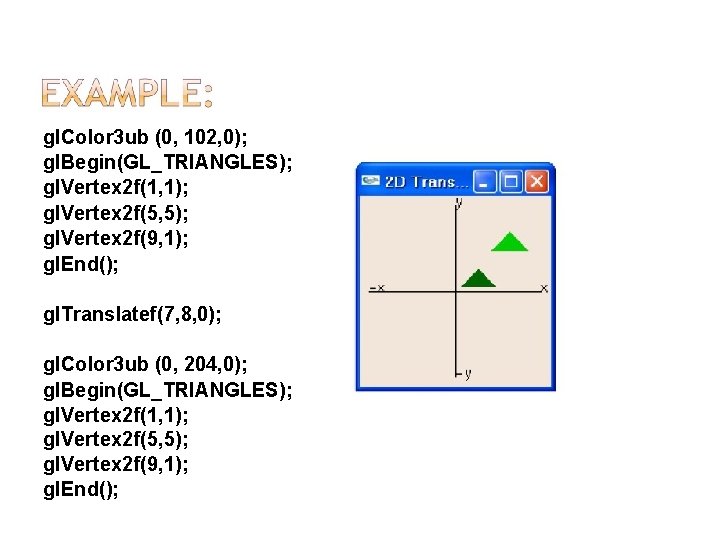
gl. Color 3 ub (0, 102, 0); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(1, 1); gl. Vertex 2 f(5, 5); gl. Vertex 2 f(9, 1); gl. End(); gl. Translatef(7, 8, 0); gl. Color 3 ub (0, 204, 0); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(1, 1); gl. Vertex 2 f(5, 5); gl. Vertex 2 f(9, 1); gl. End();

gl. Color 3 ub (204, 0, 102); glut. Solid. Torus(1. 5, 4, 15, 70); gl. Translatef(-9, -10, -2); gl. Color 3 ub(255, 67, 130); Glut. Solid. Torus(1. 5, 4, 15, 70);

The gl. Rotated, gl. Rotatef functions computes a matrix that performs a counterclockwise rotation of angle degrees about the vector from the origin through the point (x, y, z). Then multiplies the current matrix by a rotation matrix.

Float gl. Rotatef(Glfloat angle, Glfloat x , Glfloat y , Glfloat z); Double gl. Rotated(Glfloat angle, Gldouble x, Gldouble y, Gldouble z); �gl. Rotatef(Ө, 0, 0, 0) �gl. Rotatef(-Ө, 0, 0, 0) �Ө --> anticlockwise rotation �-Ө --> Clockwise rotation � 0, 0 -> x, y -> Rotation about the origin
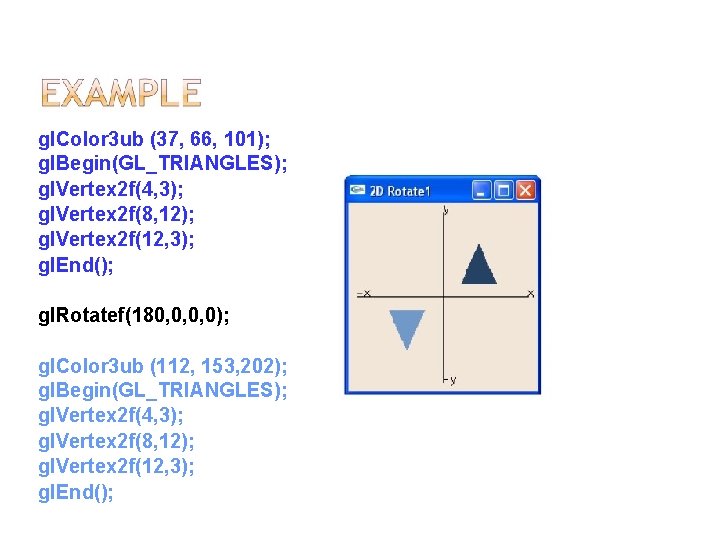
gl. Color 3 ub (37, 66, 101); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(4, 3); gl. Vertex 2 f(8, 12); gl. Vertex 2 f(12, 3); gl. End(); gl. Rotatef(180, 0, 0, 0); gl. Color 3 ub (112, 153, 202); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(4, 3); gl. Vertex 2 f(8, 12); gl. Vertex 2 f(12, 3); gl. End();

gl. Color 3 ub (37, 66, 101); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(4, 3); gl. Vertex 2 f(8, 12); gl. Vertex 2 f(12, 3); gl. End(); gl. Rotatef(180, 1, 0, 0); gl. Color 3 ub (112, 153, 202); gl. Begin(GL_TRIANGLES); gl. Vertex 2 f(4, 3); gl. Vertex 2 f(8, 12); gl. Vertex 2 f(12, 3); gl. End();

Rotation around the point is not the origin point: 1. Displacement the body until point rotation match origin point. 2. 3. Rotate the body around the origin point Inverse displacement for body (back the rotation point to its original position) Rotation around the axis In the 3 D When �gl. Rotatef(180, 1, 0, 0); � X �gl. Rotatef(180, 0, 1, 0); � Y �gl. Rotatef(180, 0, 0, 1); � Z

Rotation around the axis In the third dimension: gl. Pop. Matrix(); // x gl. Push. Matrix(); gl. Color 3 ub (153, 102, 51); gl. Rotatef(180, 1, 0, 0); gl. Translatef(8, 6, 3); glut. Solid. Teapot(4. 5); gl. Pop. Matrix(); // y gl. Push. Matrix(); gl. Color 3 ub (78, 110, 20); gl. Rotatef(180, 0, 1, 0); gl. Translatef(8, 6, 3); glut. Solid. Teapot(4. 5); gl. Pop. Matrix(); // z gl. Push. Matrix(); gl. Color 3 ub (128, 181, 33); gl. Rotatef(180, 0, 0, 1); gl. Translatef(8, 6, 3); glut. Solid. Teapot(4. 5); gl. Pop. Matrix();

The gl. Scaled and gl. Scalef functions produces a general scaling matrix along the x, y, and z axes. The three arguments indicate the desired scale factors along each of the three axes. Then multiply the current matrix by a general scaling matrix.

Float gl. Scalef(Glfloat x , Glfloat y , Glfloat z); Double gl. Scaled(Gldouble x, Gldouble y, Gldouble z); x , y , z >1 �Enlarge the size x , y , z > 0 and x , y , z <1 �Reduce the size x , y , z < 0 �Inverse

// blue TRIANGLES gl. Color 3 ub (33, 88, 104); gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(4, 3, 0); gl. Vertex 3 f(6, 6, 0); gl. Vertex 3 f(8, 3, 0); gl. End(); gl. Push. Matrix(); // Light blue gl. Scalef(2, 2. 5, 2); gl. Color 3 ub (55, 149, 175); gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(4, 3, 0); gl. Vertex 3 f(6, 6, 0); gl. Vertex 3 f(8, 3, 0); gl. End(); gl. Pop. Matrix(); // red TRIANGLES gl. Push. Matrix(); gl. Scalef(0. 5, 0. 6, 0. 5); gl. Color 3 ub (252, 20, 53); gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(4, 3, 0); gl. Vertex 3 f(6, 6, 0); gl. Vertex 3 f(8, 3, 0); gl. End(); gl. Pop. Matrix();

Scaling body for a fixed point in the second dimension : 1. Displacement the body until fixed point match origin point. 2. Change the body size 3. Inverse displacement for body (back the fixed point to its original position)

gl. Push. Matrix(); gl. Translatef(7. 5, 5. 5, 0); gl. Scalef(2, 2, 2); gl. Translatef(-7. 5, -5. 5, 0); gl. Color 3 ub (255, 130, 45); gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(4, 3, 0); gl. Vertex 3 f(7. 5, 10, 0); gl. Vertex 3 f(11, 3, 0); gl. End(); gl. Pop. Matrix(); gl. Color 3 ub (255, 51, 0); gl. Begin(GL_TRIANGLES); gl. Vertex 3 f(4, 3, 0); gl. Vertex 3 f(7. 5, 10, 0); gl. Vertex 3 f(11, 3, 0); gl. End();
- Slides: 22