Lab 4 Strings Standing Waves Modes Slinky Experiments

Lab 4: Strings • • • Standing Waves Modes Slinky Experiments 1. Frequency of Modes 2. Pulse on Slinky • Experiments with String – 1. 2. 3. 4. 5. 6. Computer as Driver Control Finding the Fundamental Mode Higher Modes The “Plucking Game” Changing the Length of the String Changing the Tension on the String Changing the Mass Per Unit Length of the String

String Oscillations on Musical Instruments • Stringed musical instruments – Can produce a single tone steadily (e. g. A @ 440 Hz) – String oscillation for a single tone • Complex • But periodic (e. g. 440 Hz) • Can a single string produce sounds at different pitches? – How? – At what frequencies? • How does the string oscillation look like? – Can they occur simultaneously? • How does the string oscillation look like? • How does the tone sound like? Demo http: //www. surendranath. org/Applets/Waves/Harmonics. Applet. html

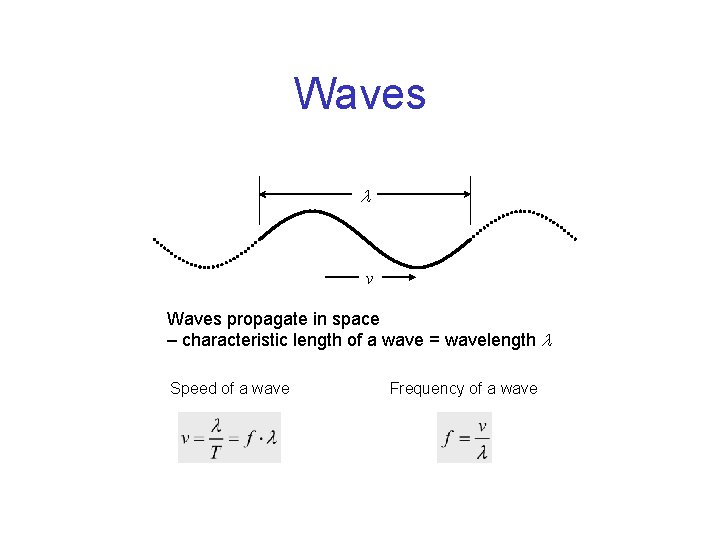
Waves v Waves propagate in space – characteristic length of a wave = wavelength Speed of a wave Frequency of a wave

Superposition Displacement “If the medium is subject to 2 or more disturbances at the same time, the net effect is to add these disturbances algebraically (with a sense of direction)”

Standing Waves (1) driving wave • Build up (superposition) of traveling waves – Driving wave & reflected wave N A N A N N: node A: antinode

Standing Waves (2) standing wave When the standing wave forms, all nodes become clear and sharp – stationary points stand out and elsewhere blurred above ~20 Hz.

Fixed-End String A 0 L x First mode (Fundamental) Second mode (First Overtone) ? Third mode (Second Overtone)

Data Table String experiments with ƒ 1 = 45 Hz case: Picture mode #, n Measured ƒ (Hz) n · measured ƒ 1 (Hz) # of nodes 1 45 1 · 45 = 45 2 2 2 · 45 = 90 3 135

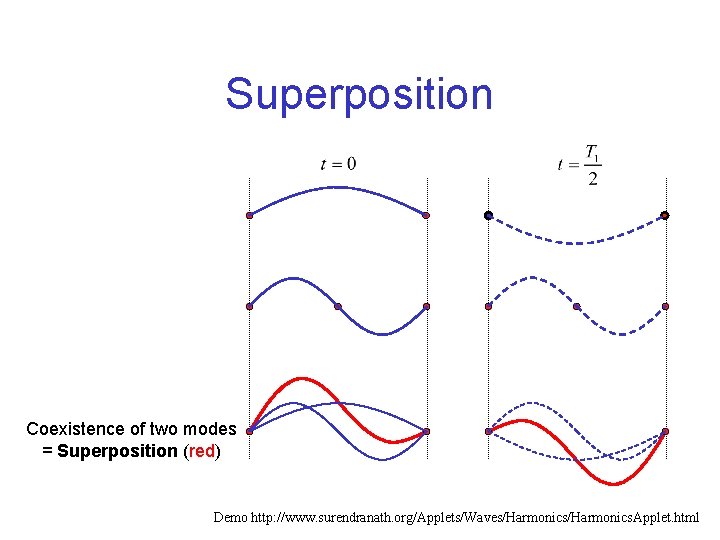
Superposition Coexistence of two modes = Superposition (red) Demo http: //www. surendranath. org/Applets/Waves/Harmonics. Applet. html