Lab 2 variable transformations LISA statistics GetisOrd statistics

Lab #2: - variable transformations - LISA statistics - Getis-Ord statistics - constructing spider diagrams Spatial statistics in practice Center for Tropical Ecology and Biodiversity, Tunghai University & Fushan Botanical Garden

SAS code for identifying a Box-Cox type of response variable transformation FILENAME INDATA ' D: JYU-SUMMERSCHOOL 2006LAB#1PR-AREAS-COMPETITION. TXT'; TITLE 'SW-BASED TRANSFORMATIONS FOR THE PR AREA DATA'; ************************ * READ IN GEOREFERENCED DATA; * * THEN CENTER THE SELEDTED ATTRIBUTE VARIABLE * ************************; DATA STEP 1; INFILE INDATA LRECL=1024; INPUT ID AREAM AREACT MCT_RATIO TRMCT_RATIO AREAPT MPT_RATIO TRMPT_RATIO NAME$; Y = AREAM; X 0=1; RUN; PROC UNIVARIATE NORMAL; VAR Y; RUN; PROC UNIVARIATE NOPRINT; VAR Y; OUTPUT OUT=TEMP MEDIAN=XM MAX=YMAX MIN=YMIN; RUN; DATA TEMP(REPLACE=YES); SET TEMP; IF YMIN>0 THEN DEC = YMAX/YMIN; ELSE DEM=YMAX; RUN; PROC PRINT; VAR DEC YMAX YMIN XM; RUN; PROC RANK DATA=STEP 1 OUT=STEP 1 (REPLACE=YES) NORMAL=BLOM; VAR Y; RANKS NY; RUN; PROC RANK DATA=STEP 1 OUT=STEP 1 (REPLACE=YES); VAR Y; RANKS RY; RUN; DATA STEP 1 (REPLACE=YES); SET STEP 1; IF _N_=1 THEN SET TEMP(KEEP=YMIN YMAX); Y=Y-YMIN; RUN;

************************** * A JACOBIAN TERM MAY BE NEEDED HERE IF N IS SMALL * ************************** * LOG TRANSFORMATION (POWER OF 0) WITH TRANSLATION * **************************; PROC NLIN DATA=STEP 1 NOITPRINT MAXITER=5000 METHOD=MARQUARDT; PARMS A=0 B=1 D=0. 01; BOUNDS 0<D; MODEL NY = A + B*LOG(Y+D); OUTPUT OUT=TEMP 1 PARMS=A B D; RUN; DATA TEMP 1(REPLACE=YES); SET TEMP 1; D=D-YMIN; RUN; PROC MEANS; VAR D; RUN; *************************** * POWER TRANSFORMATION (POWER <> 0) WITH TRANSLATION * ***************************; PROC NLIN DATA=STEP 1 NOITPRINT MAXITER=1000 METHOD=MARQUARDT; PARMS A=0 B=1 C=0. 5; D=1. 0 E-10; BOUNDS 0<D; MODEL NY = A + B*((Y + D)**C - 1)/C; OUTPUT OUT=TEMP 2 PARMS=A B D; RUN; DATA TEMP 2(REPLACE=YES); SET TEMP 2; D=D-YMIN; RUN; PROC MEANS; VAR C D; RUN; *************** * EXPONENTIAL TRANSFORMATION * ***************; PROC NLIN DATA=STEP 1 NOITPRINT MAXITER=5000 METHOD=MARQUARDT; PARMS A=0 B=1 C=0. 01; MODEL NY = A + B*EXP(-C*(Y+YMIN) ); OUTPUT OUT=TEMP PARMS=A B C; RUN; PROC MEANS; VAR C; RUN; exponent of 0 exponent of < 0, > 0 exponentiation (Manley transformation)

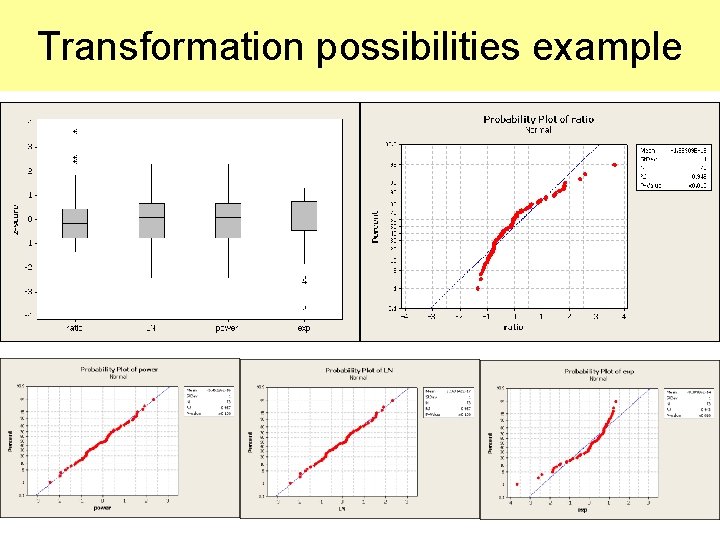
Transformation possibilities example

SAS code for normality & variance equality tests FILENAME INDATA 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-AREAS-COMPETITION. TXT'; OPTIONS LINESIZE=72; TITLE 'SW-BASED TRANSFORMATIONS FOR THE PR AREA DATA'; ************************ * READ IN GEOREFERENCED DATA; * * THEN CENTER THE SELEDTED ATTRIBUTE VARIABLE * ************************; DATA STEP 1; INFILE INDATA LRECL=1024; INPUT ID AREAM AREACT MCT_RATIO TRMCT_RATIO AREAPT MPT_RATIO TRMPT_RATIO NAME$; Y = MCT_RATIO; TRY = LOG(Y – 0. 20); X 0=1; RUN; PROC UNIVARIATE NORMAL; VAR Y TRY; RUN; PROC MEANS DATA=STEP 1 NOPRINT; VAR Y; OUTPUT OUT=YMEAN=YMEAN; RUN; DATA STEP 1(REPLACE=YES); SET STEP 1; IF _N_=1 THEN SET YMEAN(KEEP=YMEAN); IF Y>YMEAN THEN IYMEAN=1; ELSE IYMEAN=0; RUN; PROC GLM; CLASS IYMEAN; MODEL Y=IYMEAN; MEANS IYMEAN/HOVTEST=BARTLETT; RUN; PROC GLM; CLASS IYMEAN; MODEL Y=IYMEAN; MEANS IYMEAN/HOVTEST=LEVENE; RUN; PROC MEANS DATA=STEP 1 NOPRINT; VAR TRY; OUTPUT OUT=TRYMEAN=TRYMEAN; RUN; DATA STEP 1(REPLACE=YES); SET STEP 1; IF _N_=1 THEN SET TRYMEAN(KEEP=TRYMEAN); IF TRY>TRYMEAN THEN ITRYMEAN=1; ELSE ITRYMEAN=0; RUN; PROC GLM; CLASS ITRYMEAN; MODEL TRY=ITRYMEAN; MEANS ITRYMEAN/HOVTEST=BARTLETT; RUN; PROC GLM; CLASS ITRYMEAN; MODEL TRY=ITRYMEAN; MEANS ITRYMEAN/HOVTEST=LEVENE; RUN;

SAS code for Gi, LISA and z. LISA FILENAME INDATA 1 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-AREAS-COMPETITION. TXT'; FILENAME INDATA 2 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-DEM&QUAD-DATA. TXT'; FILENAME CONN 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-CON. TXT'; FILENAME OUTFILE 'D: JYU-SUMMERSCHOOL 2006LAB#2PR-LISA-OUT. TXT'; OPTIONS LINESIZE=72; TITLE 'GI AND LISA FOR THE PR AREA DATA'; ******************************************* * READ IN THE N-BY-N GEOGRAPHIC CONNECTIVITY MATRIX; MAKE SURE NOT TO MISREAD THE ID * *******************************************; DATA STEP 1; INFILE CONN; INPUT IDC C 1 -C 73; RUN; ************************************** * READ IN GEOREFERENCED DATA; THEN CENTER THE SELECTED ATTRIBUTE VARIABLE * **************************************; DATA STEP 2 A; INFILE INDATA 1 LRECL=1024; INPUT POLYGON AREAM AREACT MCT_RATIO TRMCT_RATIO AREAPT MPT_RATIO TRMPT_RATIO NAME$; * Y = AREAM; * Y = MCT_RATIO; X 0=1; RUN; PROC SORT DATA=STEP 2 A OUT=STEP 2 A(REPLACE=YES); BY NAME; RUN; DATA STEP 2 B; INFILE INDATA 2 LRECL=1024; INPUT IDDEM MELEV SELEV U V QUAD NAME$; U=U/1000; V=V/1000; Y=LOG(MELEV+17. 5); * Y=(SELEV-25)**0. 5; YO=Y; RUN; PROC SORT DATA=STEP 2 B OUT=STEP 2 B(REPLACE=YES); BY NAME; RUN; DATA STEP 2; MERGE STEP 2 A STEP 2 B; BY NAME; RUN;

PROC DATA STANDARD MEAN=0 STD=1 OUT=STEP 2(REPLACE=YES); VAR Y; RUN; MEANS DATA=STEP 2 NOPRINT; VAR X 0; OUTPUT OUT=NOUT SUM=N; RUN; MEANS DATA=STEP 2 NOPRINT; VAR YO; OUTPUT OUT=YOOUT MEAN=YOBAR USS=YOUSS; RUN; STEP 2(REPLACE=YES); SET STEP 2; SET STEP 1; ARRAY CONN{73} C 1 -C 73; ARRAY YCONN{73} CY 1 -CY 73; ARRAY YOCONN{73} CYO 1 -CYO 73; CSUM = 0; DO I=1 TO 73; CSUM = CSUM + CONN{I}; IF _N_=I THEN CONN{I}=0; YCONN{I} = Y*CONN{I}; YOCONN{I} = YO*CONN{I}; END; RUN; PROC DATA MEANS DATA=STEP 2 NOPRINT; VAR CY 1 -CY 73; OUTPUT OUT=CYOUT 1 SUM=CY 1 -CY 73; RUN; TRANSPOSE DATA=CYOUT 1 PREFIX=CY OUT=CYOUT 2; VAR CY 1 -CY 73; RUN; MEANS DATA=STEP 2 NOPRINT; VAR CYO 1 -CYO 73; OUTPUT OUT=CYOOUT 1 SUM=CYO 1 -CYO 73; RUN; TRANSPOSE DATA=CYOOUT 1 PREFIX=CYO OUT=CYOOUT 2; VAR CYO 1 -CYO 73; RUN; STEP 3; SET STEP 2(KEEP=POLYGON Y YO CSUM); SET CYOUT 2(KEEP=CY 1); SET CYOOUT 2(KEEP=CYO 1); IF _N_=1 THEN SET NOUT(KEEP=N); would be (n-2) IF _N_=1 THEN SET YOOUT(KEEP=YOBAR YOUSS); for an unbiased LISA=Y*CY 1/((N-1)/N); estimate ELISA=-CSUM/(N-1); GI=(CYO 1 -((N*YOBAR-YO)/(N-1))*CSUM)/ ( SQRT((YOUSS-YO**2 -((N*YOBAR-YO)**2)/(N-1))*SQRT(((N-1)*CSUM-CSUM**2)/(N-2)) ); DROP CY 1; RUN; PROC PRINT; VAR LISA GI; RUN;

*************** * CONDITIONAL RANDOMIZATION * ***************; PROC TRANSPOSE DATA=STEP 3 PREFIX=N OUT=SAMPLE 1; VAR CSUM; RUN; PROC TRANSPOSE DATA=STEP 3 PREFIX=Y OUT=SAMPLE 2; VAR Y; RUN; DATA SAMPLE 3; SET SAMPLE 1; SET SAMPLE 2; ARRAY TY{73} Y 1 -Y 73; ARRAY NI{73} N 1 -N 73; DO I=1 TO 73; reduce to 100 for class purposes DO J=1 TO 10000; DO K=1 TO 73; YI=TY{I}; YJ=TY{K}; PROB = RANUNI(0); IF K=I THEN PROB=0; NUMI=NI{I}; OUTPUT; END; DROP K Y 1 -Y 73 N 1 -N 73; RUN; PROC RANK DATA=SAMPLE 3 OUT=SAMPLE 3 (REPLACE=YES) DESCENDING; VAR PROB; RANKS RPROB; BY I J; RUN; DATA SAMPLE 3(REPLACE=YES); SET SAMPLE 3; IF _N_=1 THEN SET NOUT(KEEP=N); IF RPROB > NUMI THEN DELETE; YIYJ=YI*YJ/((N-1)/N); RUN; PROC MEANS NOPRINT; VAR YIYJ; BY I J; OUTPUT OUT=SAMPLE 4 SUM=CYIYJ; RUN; PROC MEANS NOPRINT; VAR CYIYJ; BY I; OUTPUT OUT=SAMPLE 5 MEAN=MCYIYJ STD=SCYIYJ; RUN;

DATA FINAL; SET STEP 3(KEEP=POLYGON LISA ELISA N); SET SAMPLE 5(KEEP=MCYIYJ SCYIYJ); ZLISA = (LISA-MCYIYJ)/SCYIYJ; IF ZLISA> 0 THEN PROBLISA = 1 - PROBNORM(ZLISA); ELSE PROBLISA = PROBNORM(ZLISA); BON 1 = 0. 05/N; BON 2 = 1 - 0. 01/N; SIDAK 1 = 1 - (1 - 0. 05)**(1/N); SIDAK 2 = (1 - 0. 05)**(1/N); IF PROBLISA < BON 1 OR PROBLISA < SIDAK 1 OR PROBLISA > BON 2 OR PROBLISA > SIDAK 2 THEN IEXTREME=1; ELSE IEXTREME=0; RUN; PROC PRINT; VAR POLYGON LISA ZLISA PROBLISA IEXTREME BON 1 BON 2 SIDAK 1 SIDAK 2; RUN; DATA EXTREMES; SET FINAL; IF IEXTREME=0 THEN DELETE; RUN; PROC PRINT; VAR POLYGON LISA ZLISA PROBLISA IEXTREME BON 1 BON 2 SIDAK 1 SIDAK 2; RUN; PROC CLUSTER DATA=FINAL NOPRINT SIMPLE METHOD=COMPLETE NOEIGEN OUTTREE=LISATREE; VAR ZLISA; ID POLYGON; RUN; ************** * SET THE NUMBER OF GROUPS * **************; PROC TREE DATA=LISATREE OUT=TREEOUT NCLUSTERS=5; ID POLYGON; RUN; PROC SORT OUT=TREEOUT; BY POLYGON; RUN; DATA PROC PROC FINAL(REPLACE=YES); MERGE FINAL TREEOUT; BY POLYGON; RUN; SORT OUT=FINAL(REPLACE=YES); BY CLUSTER ZLISA; RUN; ANOVA; CLASS CLUSTER; MODEL ZLISA=CLUSTER; RUN; MEANS DATA=FINAL NOPRINT; VAR ZLISA; BY CLUSTER; OUTPUT OUT=TEMP MIN=ZMIN MAX=ZMAX; RUN; PRINT; RUN; UNIVARIATE DATA=FINAL NOPRINT; VAR ZLISA; BY CLUSTER; OUTPUT OUT=TEMP 2 PROBN=SW; RUN; PRINT; RUN; DISCRIM DATA=FINAL POOL=TEST; CLASS CLUSTER; VAR ZLISA; RUN; DATA _NULL_; SET FINAL; FILE OUTFILE; PUT CLUSTER POLYGON ZLISA; RUN;

SAS code for Moran scatterplot regression diagnostics FILENAME INDATA 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-DEM&QUAD-DATA. TXT'; FILENAME CONN 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-CON. TXT'; FILENAME OUTFILE 'D: JYU-SUMMERSCHOOL 2006LAB#2PR-REGRESSION-DIAGNOSTICS. TXT'; TITLE 'MORAN SCATTERPLOT REGRESSION DIAGNOSTICS FOR THE PR DATA'; ******************************* * READ IN THE N-BY-N GEOGRAPHIC CONNECTIVITY MATRIX; * *******************************; DATA STEP 1; INFILE CONN LRECL=512; INPUT IDC C 1 -C 73; ARRAY CONN{73} C 1 -C 73; CSUM = 0; DO I=1 TO 73; CSUM = CSUM + CONN{I}; END; RUN; PROC MEANS DATA=STEP 1 NOPRINT; VAR CSUM; OUTPUT OUT=CSUM SUM=SUMCSUM; RUN; PROC PRINT; RUN; ************************************** * READ IN GEOREFERENCED DATA; THEN CENTER THE SELECTED ATTRIBUTE VARIABLE * **************************************; DATA STEP 2; INFILE INDATA; IDDEM is INPUT IDDEM MELEV SELEV U V QUAD NAME$; U=U/1000; V=V/1000; Y=LOG(MELEV+17. 5); * Y=(SELEV-25)**0. 5; X 0=1; RUN; PROC SORT OUT=STEP 2(REPLACE=YES); BY IDDEM; RUN; PROC STANDARD MEAN=0 STD=1 OUT=STEP 2(REPLACE=YES); VAR Y; RUN; PROC MEANS NOPRINT; VAR X 0; OUTPUT OUT=OUTN SUM=N; RUN; the unique id

DATA STEP 2(REPLACE=YES); SET STEP 2; SET STEP 1; ARRAY CONN{73} C 1 -C 73; ARRAY YCONN{73} CY 1 -CY 73; DO I=1 TO 73; YCONN{I} = Y*CONN{I}; END; RUN; PROC MEANS NOPRINT; VAR CY 1 -CY 73; OUTPUT OUT=CYOUT 1 SUM=CY 1 -CY 73; RUN; PROC TRANSPOSE DATA=CYOUT 1 PREFIX=CY OUT=CYOUT 2; VAR CY 1 -CY 73; RUN; DATA STEP 3; SET STEP 2(KEEP=X 0 Y CSUM); SET CYOUT 2(KEEP=CY 1); CZY=CY 1; ZY=Y; RUN; PROC REG OUTEST=OUTREG; MODEL CZY=ZY/NOINT PRESS; OUTPUT OUT=MCPRED P=CZYHAT H=HI RSTUDENT=RSTUDENTI DFFITS=DFFITSI; RUN; DATA OUTREG(REPLACE=YES); SET OUTREG; SET OUTN(KEEP=N); RMSEPRESS=SQRT(_PRESS_/N); RUN; PROC PRINT DATA=OUTREG; VAR _RMSE_ RMSEPRESS; RUN; DATA _NULL_; SET MCPRED; SET STEP 2(KEEP=IDDEM NAME); FILE OUTFILE; PUT IDDEM HI RSTUDENTI DFFITSI NAME; RUN; DATA MCPRED(REPLACE=YES); SET MCPRED; IF _N_=1 THEN SET OUTN(KEEP=N); IF HI<2*1/N THEN HI='. '; IF ABS(RSTUDENTI) < 2 THEN RSTUDENTI='. '; IF DFFITSI < 2/SQRT(1/N) THEN DFFITSI='. '; RUN; DATA CHECK; SET MCPRED; SET STEP 2(KEEP=IDDEM NAME); IF HI='. ' AND RSTUDENTI='. ' AND DFFITSI='. ' THEN DELETE; RUN; PROC PRINT DATA=CHECK; VAR IDDEM HI RSTUDENTI DFFITSI NAME; RUN;

SAS code for local statistics eigenvector covariates FILENAME EVECS 'D: JYU-SUMMERSCHOOL 2006LAB#1PR-EIGENVECTORS. TXT'; FILENAME LISA 'D: JYU-SUMMERSCHOOL 2006LAB#2PR-LISA-OUT. TXT'; FILENAME REGD 'D: JYU-SUMMERSCHOOL 2006LAB#2PR-REGRESSION-DIAGNOSTICS. TXT'; FILENAME OUTFILE 'D: JYU-SUMMERSCHOOL 2006LAB#2PR-SELECTED-EVECS. TXT'; TITLE 'SPATIAL AUTOCORRELATION IN PR MORAN SCATTERPLOT DIAGNOSTICS'; *************************** * READ IN EIGENVECTORS, LISA, REGRESSION DIAGNOSTICS * ***************************; DATA STEP 1; INFILE EVECS LRECL=1024; INPUT IDE E 1 -E 73; RUN; PROC SORT OUT=STEP 1(REPLACE=YES); BY IDE; RUN; DATA STEP 2; INFILE LISA; INPUT CLUSTER IDL ZLISA; RUN; PROC SORT OUT=STEP 2(REPLACE=YES); BY IDL; RUN; DATA STEP 3; INFILE REGD; INPUT IDR HI RSTUDENTI DFFITSI; RUN; PROC SORT OUT=STEP 3(REPLACE=YES); BY IDR; RUN; DATA FINAL; SET STEP 1; SET STEP 2; SET STEP 3; RUN; PROC PRINT; VAR IDE IDL IDR; RUN; PROC REG; MODEL ZLISA = E 1 -E 73/SELECTION=STEPWISE SLE=0. 01; OUTPUT P=ZLISAHAT; RUN; PROC GPLOT; PLOT ZLISA*ZLISAHAT ZLISA*ZLISA/OVERLAY; RUN; PROC REG; MODEL HI = E 1 -E 73/SELECTION=STEPWISE SLE=0. 01; OUTPUT P=HIHAT; RUN; PROC GPLOT; PLOT HI*HIHAT HI*HI/OVERLAY; RUN; PROC REG; MODEL RSTUDENTI = E 1 -E 73/SELECTION=STEPWISE SLE=0. 01; OUTPUT P=RSTHAT; RUN; PROC GPLOT; PLOT RSTUDENTI*RSTHAT RSTUDENTI*RSTUDENTI/OVERLAY; RUN; PROC REG; MODEL DFFITSI = E 1 -E 73/SELECTION=STEPWISE SLE=0. 01; OUTPUT P=DFFITSHAT; RUN; PROC GPLOT; PLOT DFFITSI*DFFITSHAT DFFITSI*DFFITSI/OVERLAY; RUN; DATA _NULL_; SET FINAL(KEEP=IDE E 2); FILE OUTFILE; PUT IDE E 2; RUN; OUT=OUTLISA OUT=OUTHI OUT=OUTRST OUT=OUTDFFITS

Arc. GIS 9. 1: LISA & Getis-Ord Gi This is to be fully functional in Arc. GIS 9. 2!

Constructing spider diagrams in Arc. View • Enable Geoprocessing extension • Use Geoprocessing Wizard to disolve areal units on the basis of some grouping • Enable “Add true X, Y Centroid” extension • Compute centroids of disolved *. shp map • RUN spider diagram script to add “event themes” from original map (centers) and disolved map (points)

What you should have learned in today’s lab: 1. Identify power transformation for variables 2. Calculate normality and variance equality (attribute and geographic) diagnostics 3. Reconstruct the Moran scatterplots and the semivariogram plots 4. Calculate and map Gi, LISA and regression diagnostic statistics 5. The ability to construct spider diagrams