Lab 11 Maps and Scales Objectives O 1

Lab 11 Maps and Scales Objectives: O 1: Review the metric system and conversions O 2: Learn about map scales (= image scale when working with images) O 3: Review angular distances in degrees/arcminutes/arcseconds, and in decimal degrees. O 4: Check your angular distances against software 1

Metric Units - length millimeters (mm) = 1/1000 m centimeters (cm) = 1/100 m meters (m) = 1000 mm, 100 cm kilometers (km) = 1000 m Metric Units - mass gram (g) kilogram (kg) =1000 g Metric Units - time seconds (s) Every number you provide in this lab must have appropriate units, or it is wrong. Not a warning, just how things are. 4

Unit Conversions The length of this room is about 9 yards. Convert this to inches. . . Multiply 9 yards by “one” 3 feet Length = 9 yards x 1 yard ( 1 yard Length = 9 yards x 3 feet ( Length = 27 feet x ( 12 in 1 foot ) = 27 feet ) = 3 yards /feet 2 ) = 324 inches 300 inches 4

Unit Conversions Watch the beauty of the metric system. The distance to the moon is 384, 000 km. Convert this to cm. Start with the conversions: 1 km = 1000 m 1 m = 100 cm Distance = 384, 000 km x 384, 000 m x ( ( 100 cm 1 m 1000 m 1 km ) = 384, 000 m ) = 38, 400, 000 cm

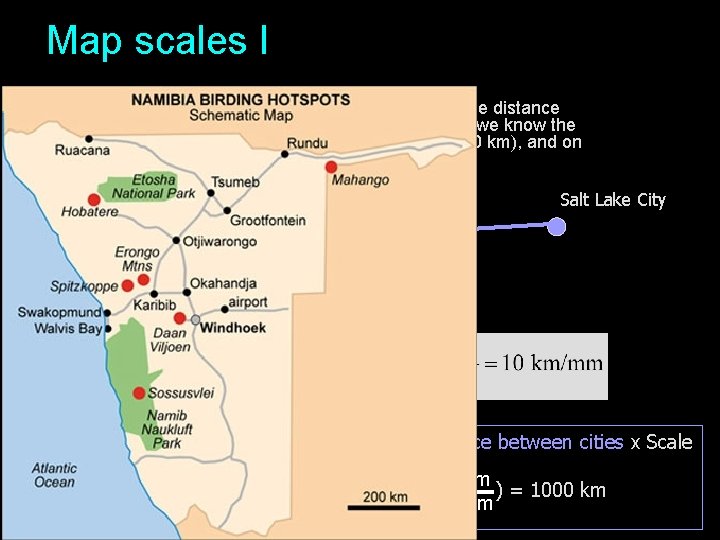
Map scales I On a map of the U. S. A. , we want to determine the distance from Sacramento to Salt Lake City. In this case, we know the distance from Sacramento to San Francisco (150 km), and on the map they are separated by 15 mm. 15 mm San Francisco Sacramento 100 mm Salt Lake City 150 km Distance from Sacramento to Salt Lake City = Measured distance between cities x Scale = (100 mm)(10 km ) = 1000 km mm

Map Scale II Moon map scale = 1: 2, 500, 000 1 cm on the map corresponds to 2, 500, 000 cm in the real world. 5

Map Scale II Moon map scale = 1: 2, 500, 000 10. 3 cm Suppose you measure a crater to be 10. 3 cm across on a map: To convert this into a real-world size, multiply your measure by the map scale: 2, 500, 000 cm (real world) 10. 3 cm (map) x 1 cm (map) ( )= = 25, 750, 000 cm (real world) = 257. 5 km = 258 km 5

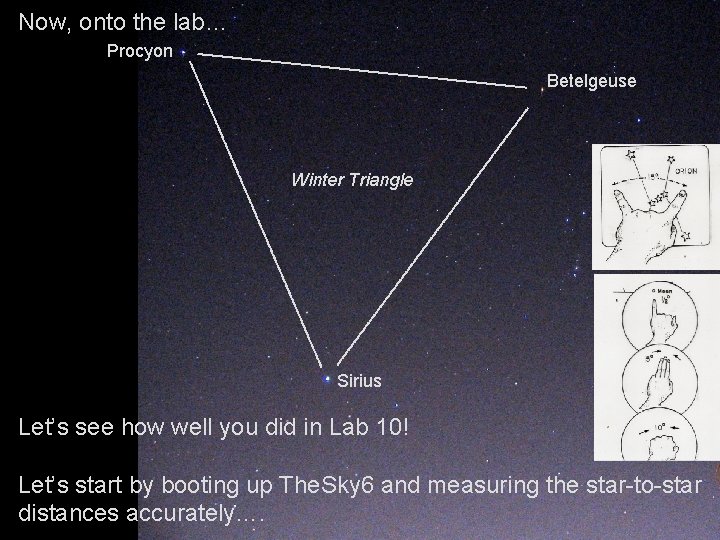
Now, onto the lab… Procyon Betelgeuse Winter Triangle Sirius Let’s see how well you did in Lab 10! Let’s start by booting up The. Sky 6 and measuring the star-to-star distances accurately….

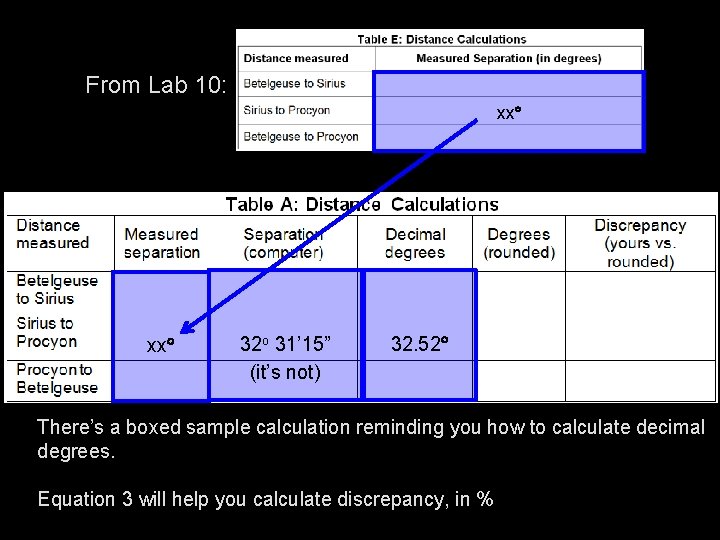
From Lab 10: xx 32 o 31’ 15” (it’s not) 32. 52 There’s a boxed sample calculation reminding you how to calculate decimal degrees. Equation 3 will help you calculate discrepancy, in %

Decimal degrees Suppose you measured some angle between stars as: 32 o 31’ 15” Let’s convert this to Decimal Degrees First, convert the 15” to arc minutes: 15” x 1’ = 0. 25’ 60” Add that to 31’: 31’ + 0. 25’ = 31. 25’ 32 o 31. 25’ Next, convert the 31. 25’ to degrees: 1 o 31. 25’ x 60’ = 0. 5208 o Add that to 32 o: o = 32. 52 o 32 o + 0. 5208 o = 32. 5208 32 32 5

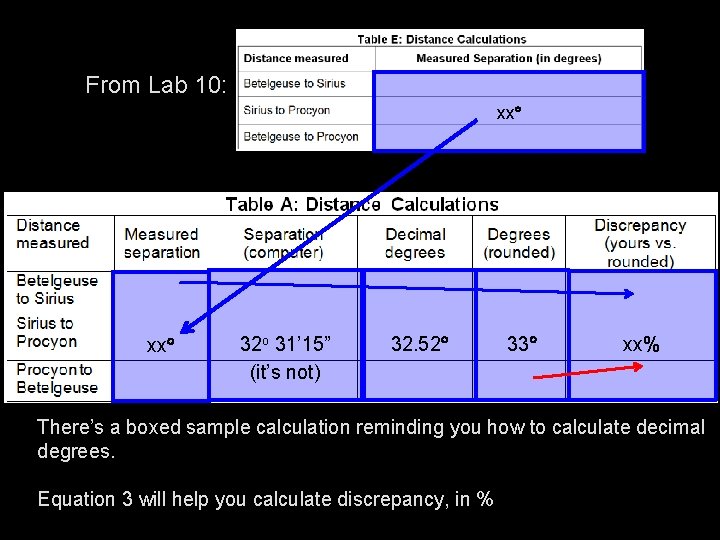
From Lab 10: xx 32 o 31’ 15” (it’s not) 32. 52 33 xx% There’s a boxed sample calculation reminding you how to calculate decimal degrees. Equation 3 will help you calculate discrepancy, in %

Measure in mm for Table B

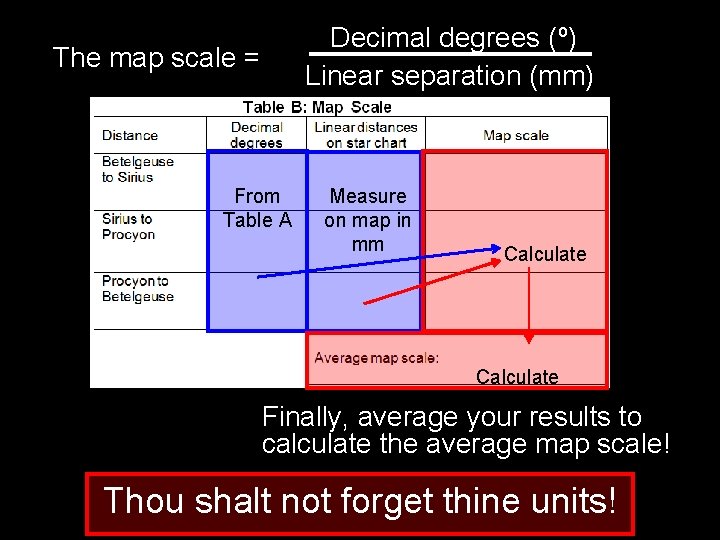
Decimal degrees (º) Linear separation (mm) The map scale = From Table A Measure on map in mm Calculate Finally, average your results to calculate the average map scale! Thou shalt not forget thine units!

From Map Calculate