Lab 10 Arithmetic Systems Slide 2 Adder System

Lab 10 : Arithmetic Systems : Slide #2 Adder System Layout: Slide #3 2’s Complement Conversions: Slide #4 Arithmetic Overflow: Slide #5 8 Bit Adder/Subtractor System:
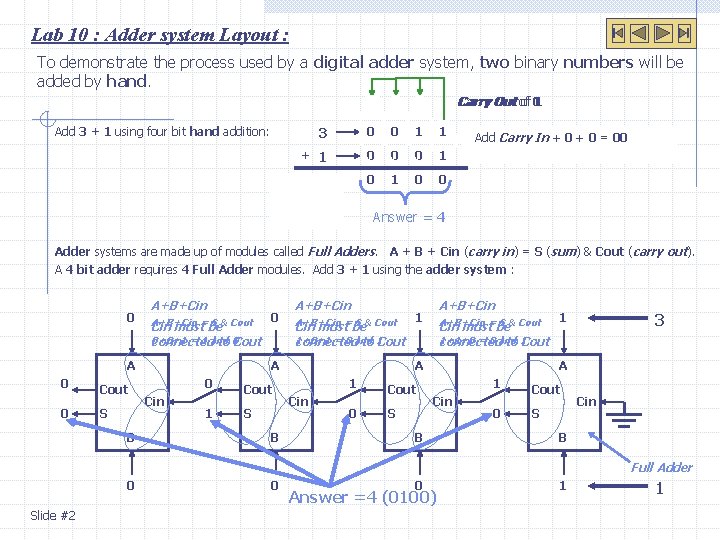
Lab 10 : Adder system Layout : To demonstrate the process used by a digital adder system, two binary numbers will be added by hand. Carry Out of of 0 11 0 1 1 3 0 0 1 1 + 1 0 0 0 1 0 0 Add 3 + 1 using four bit hand addition: 0 Ignore the Carry Out Addthe Carry 2 LSB’s. In In++1 1+1=10 0++00==10 (200 01 in binary) …or… 1+1 = 0 and a carry out of 1. Answer = 4 Adder systems are made up of modules called Full Adders. A + B + Cin (carry in) = S (sum) & Cout (carry out). A 4 bit adder requires 4 Full Adder modules. Add 3 + 1 using the adder system : 0 A+B+Cin = S & Cout Cin must be 0+0+1 = 1 and connected to 0 Cout A 0 0 Cout S B 0 A+B+Cin = S & Cout Cin must be 1+0+1 = 0 and connected to 1 Cout A 0 Cin 1 Cout S B A+B+Cin 1 A+B+Cin = S & Cout Cin must be 1+1+0 = 0 and connected to 1 Cout A 1 Cin 0 Cout S 3 1 A 1 Cin B 0 Cout S Cin B Full Adder 0 Slide #2 0 0 Answer =4 (0100) 1 1

Lab 10: 2’s Complement Conversion : Signed numbers encoded using 2’s complement notation can be added and subtracted using one process: “The process of addition”. Converting numbers to 2’s complement form is easy. Sign Bit Positive Numbers: Example: Convert +22 into 8 bit 2’s complement form. Rule : 2’s complement notation = Binary Notation. 0 Process: Write 22 as a 7 bit number. Make the Sign Bit =0 to denote 4 2 1 0 0 1 Sign Bit 64 32 16 Negative Numbers: Example: Convert -22 into 8 bit 2’s complement form. Rule : 2’s complement notation is NOT= Binary Notation. You must use a 3 step procedure to convert the negative number. Step 1: Write – 22 as an 8 bit positive number From the work above: +22 = 0 0010110 Step 2: Invert all bits The result of this process is called 1’s complement notation. Step 3: Add 1 to this new binary pattern Thus -22 = 1 1101010 in 8 bit 2’s complement notation. Theory: Adding a positive and a negative 2’s comp. number will subtract the 2 numbers. Test the Theory: Try 22+(-22) Slide #3 8 0+ 0+ 16+ 0+ 4+ 2 +0 = 22 a positive number and your done! Thus +22 = 0 0010110 in 8 bit 2’s complement notation. At first glance it does not appear to work. The 1 in the MSB is actually a carry out and can be ignored! 64 32 16 8 4 2 1 0 0 0 1 1 1 0 1 0 0 1 + 1 1 0 1 0 0 0 1 1 0 +22 + 1 1 1 0 1 0 -22 1 0 0 0 0 Answer = 0 0

Lab 10: Arithmetic Overflow is an error that occurs when 2 numbers being added together generate an answer that requires more bits than are available for the answer. numbers always wraps around to the negative Overflow from 2 positive negative numbers always wraps around to the end of theend number In our example 9 + 8 =(– 9) -15. + (-8) = +15. positive of theline. number line. For example 5 bit signed numbers will be used to demonstrate arithmetic overflow. -15 (-9)+(-8) 8+9 +15 line. falls in the NO overflow! The valid range of 5 bit numbers is. Answer – 16 to always +15. The range canmiddle be represented using a number One number on this side -16 -14 -12 -10 -8 -6 -4 -2 0 +2 +4 +6 +8 +10 +12 +15 One number on this side Add 9+8. Each number on there own is 4 a valid 5 bit number but there sum (17) exceeds the valid range. 16 (2 ) –ve #s. 16 number (24) +ve #s. invert and +1 and it will The sum turns out to be a negative number. To check which negative it is: convert to its equivalent +ve number. Sign Bit 8 4 2 1 9 0 1 0 0 1 + 8 0 1 0 0 0 1 1 0 0 1 0 1 1 0 +1 0 1 1 Negative # Invert Add 1 15 If the error goes undetected then the system would calculate 9+8 = -15 Error! Detecting Arithmetic Overflow errors is easy. All calculators and computers do it. Overflow never occurs if the 2 numbers being added have opposite sign bits. Think about it using the number line. One number on the positive side and the other on the negative side always generates a sum in between Overflow may occur if the 2 numbers being added have the same sign bits. Think about it using the number line. Both numbers from the positive side may generate a sum that exceeds +15. Both numbers from the negative side may generate a sum that exceeds -16. Slide #4 An overflow detection system checks the logic level of each number’s sign bit. If they are the same then it checks the sign bit of the answer. If the sign bit of the answer is different than the sign bit of each number then overflow has occurred and the system generates an error message.

Lab 10: 8 Bit Adder/Subtractor : Two 4 -bit adders are combined with XOR gates to create an 8 -bit adder/subtractor system. The system will be used to add 12 + (-4) and then subtract 12 – (-4). Sign Bit Load the data registers with the 2 numbers: +12 and – 4. 64 32 16 8 4 2 1 Put the system in the ADD mode. ADD/SUB =0. The XOR +12 +4 gates 0 are 0 controlled 0 0 1 0 inverters 1 0 and 0 will pass the number – 4 to the adders. Add the numbers and show the response at the SInvert output of the 1 adders. 1 1 0 1 1 Put the system in the SUB mode. ADD/SUB =1. The Add. XOR 1 gates 1 are 1 controlled 1 1 1 inverters 1 0 and 0 will pass the inverse of the number – 4 to the adders. This will make the system subtract 12 -(-4). 1 1 1 0 1 C 0 Add the numbers the response B at the S output of the adders. 1 1 and 0 1 show 0 1 Register + 1 Register A 0 1 0 0 0 1 C 0 1 1 C 4 1 0 Register B 0 0 0 1 1 Register B + 0 0 Register 1 1 1 0 0 -4 + 1 1 0 0 Register A A 0 C 4 0 0 0 C 4 1 0 0 0 1 0 1 10 01 1 0 1 1 1 0 0 00 00 00 10 Answerisis 16 8 [12+(-4)] [12 -(-4)] 1 0 0 0 Slide #5 1 0 0 1 1 0 0 0 +12
- Slides: 5