Lab 1 Egg Float Challenge Scientific Method in

Lab #1 Egg Float Challenge?

Scientific Method in Action: Oh Deer! You Smell! • Read the following article • On the paper, mark an ◦ ◦ “E” for experiment “C” for the control “R” for results “N” for conclusion ◦ Write what their hypothesis might have been

Scientific “Method? ” • Not always the same process or order! • But…always QUESTIONS and OBSERVATIONS

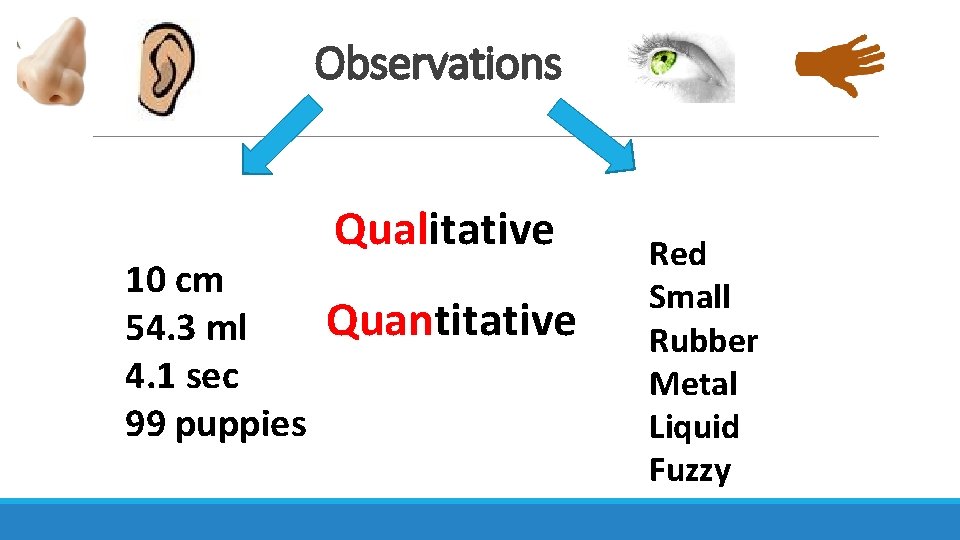
Observations 10 cm 54. 3 ml 4. 1 sec 99 puppies Qualitative Quantitative Red Small Rubber Metal Liquid Fuzzy

Experimentation • Independent variable (what you manipulate) ◦ Your “treatment” ◦ Ex. How much fertilizer, type or dosage of medicine, hours of sunlight, etc. • Dependent variable (what responds) ◦ Ex. Plant height, weight gain, animal mortality

Control • Something you don’t change for a comparison e. g. Does fertilizer help the plant grow taller? a. Water only b. Water + fertilizer

Replication Should be repeatable! - What if have one Water + fertilizer Control (water) lame plant seed and one great one?

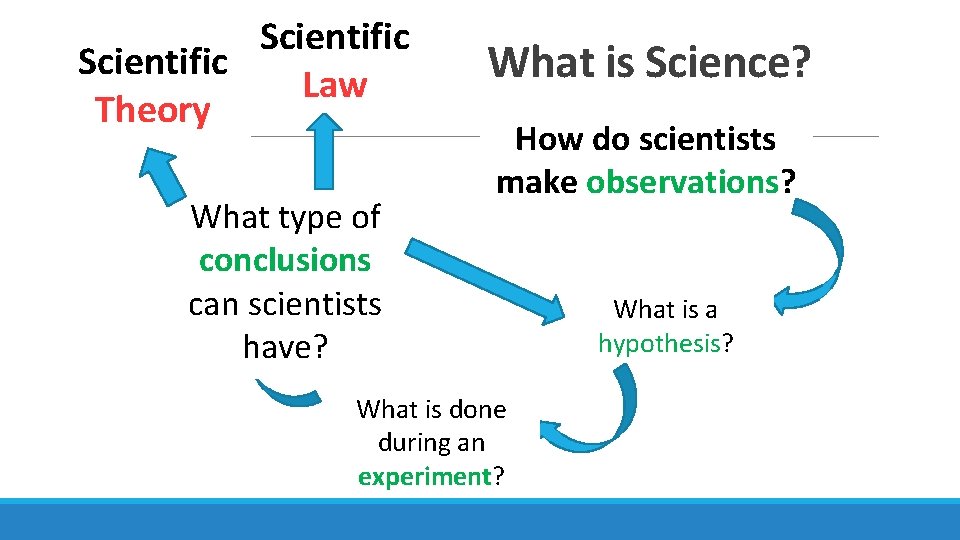
Scientific Law Theory What type of conclusions can scientists have? What is Science? How do scientists make observations? What is done during an experiment? What is a hypothesis?

Conclusions Law • DESCRIBES phenomena • Lots of data • “law of nature” Theory • Lots of observations and experiments • Tries to EXPLAIN phenomena

Quantitative (#) Observations How tall are you? How long is a class period? How much does a pound of feathers weigh? =Measurements!

Every measurement has a number and a UNIT 2. 4 L 3 puppies 3, 000 m/s How could 1 + 1 = 3? 1 person + 1 couple = 3 people

“No-No’s” for science!! Pounds (lbs) Ounces (oz) Gallons (gal) Pints, quarts, cups Feet (ft) Inches (in) Yards (yds) Miles (mi)

Systeme Internationale d’Unites (SI, metric) Copy this into the back of your Chem notebook (also found on page 34)

Certain vs. Estimated Digits in a Measurement – Write down your observation Length = 3. 3 cm 0 1 2 3 4 5 6

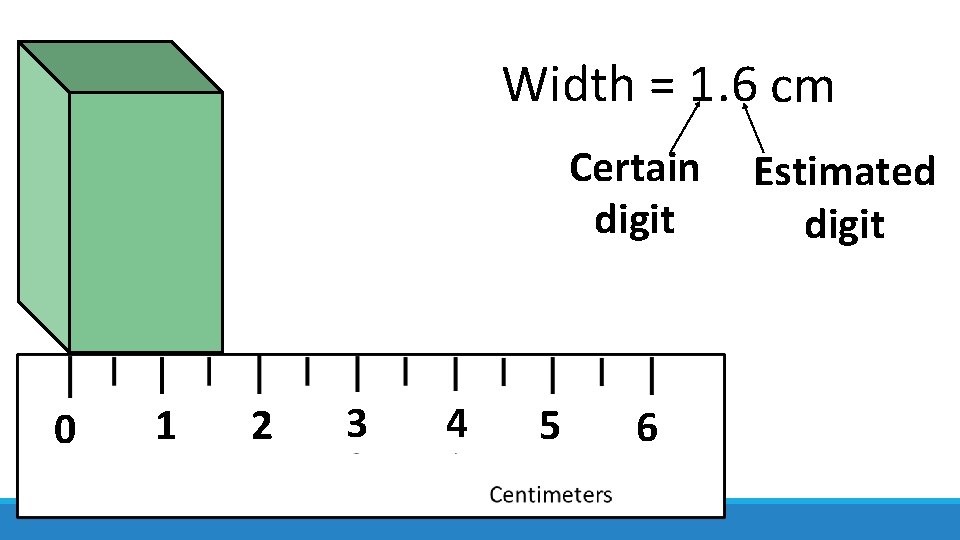
Width = 1. 6 cm Certain digit 0 1 2 3 4 5 6 Estimated digit

Mass on a Triple Beam Balance 2. 40 g 60 g =62. 40 g

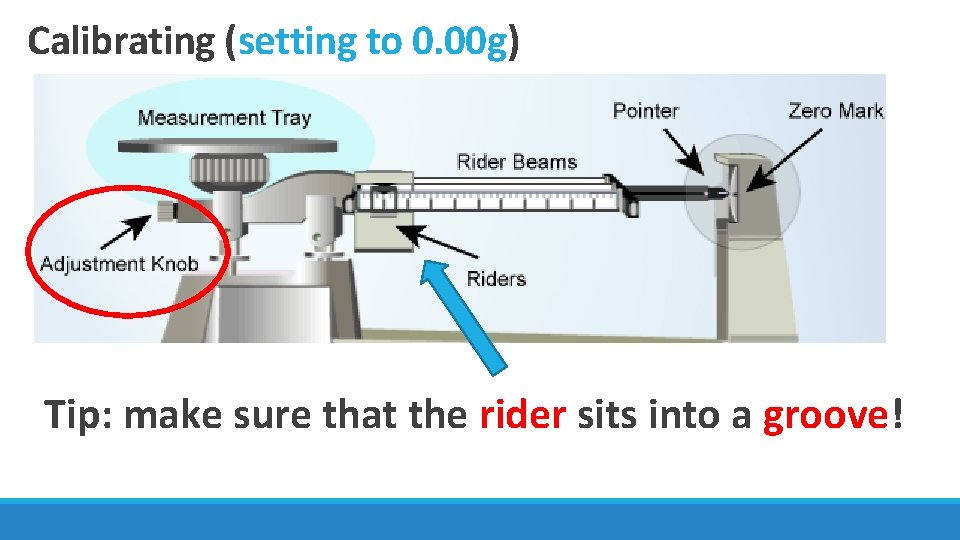
Calibrating (setting to 0. 00 g) Tip: make sure that the rider sits into a groove!

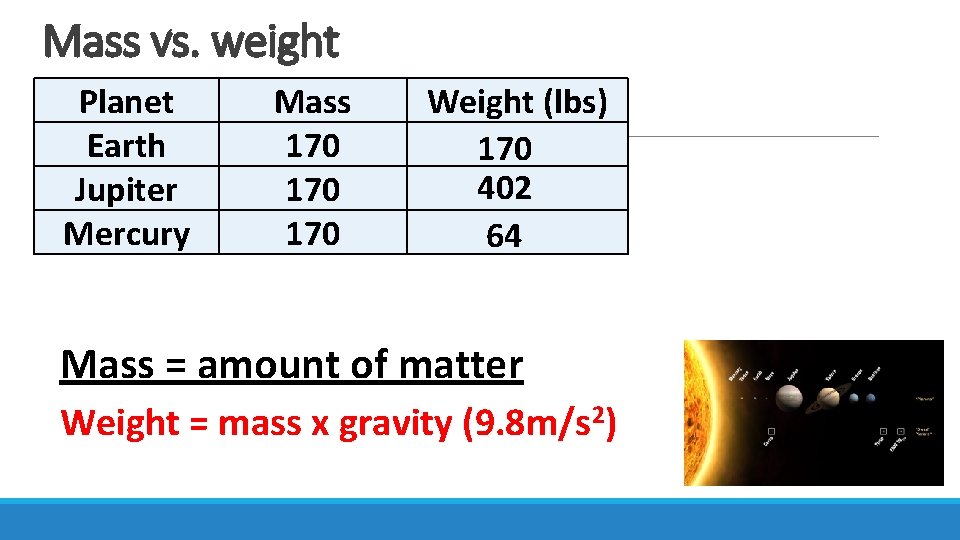
Mass vs. weight Planet Earth Jupiter Mercury Mass 170 170 Weight (lbs) 170 402 64 Mass = amount of matter Weight = mass x gravity (9. 8 m/s 2)

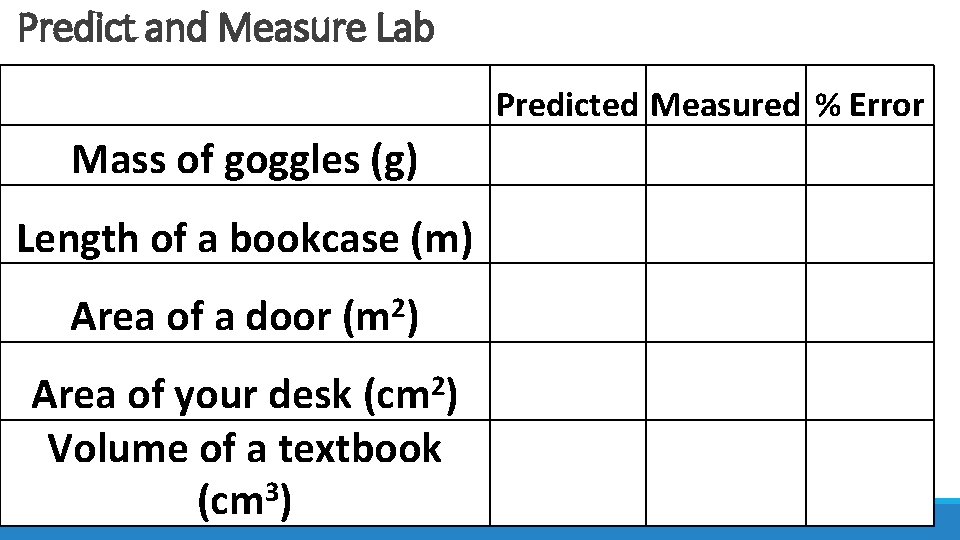
Predict and Measure Lab Predicted Measured % Error Mass of goggles (g) Length of a bookcase (m) Area of a door (m 2) 2 (cm ) Area of your desk Volume of a textbook (cm 3)

Percent error- copy this % Error = Predicted – Measured Ex. x 100 90 – 108 x 100 = % error 108

Meter Sticks in centimeters (cm)What are these two values a. _______ b. _______

Meter Sticks in meters (m) What are these two values a. _______ b. _______

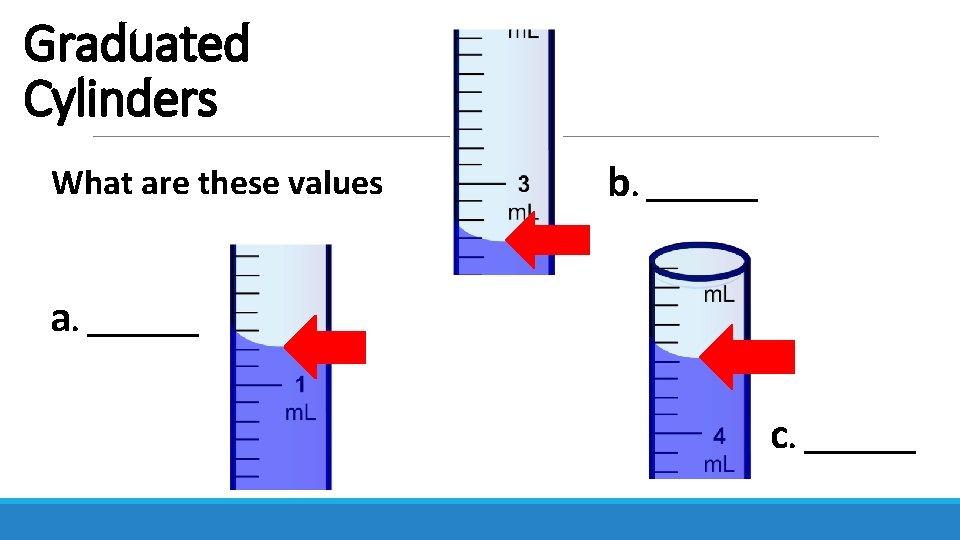
Graduated Cylinders What are these values b. _______ a. _______ c. _______

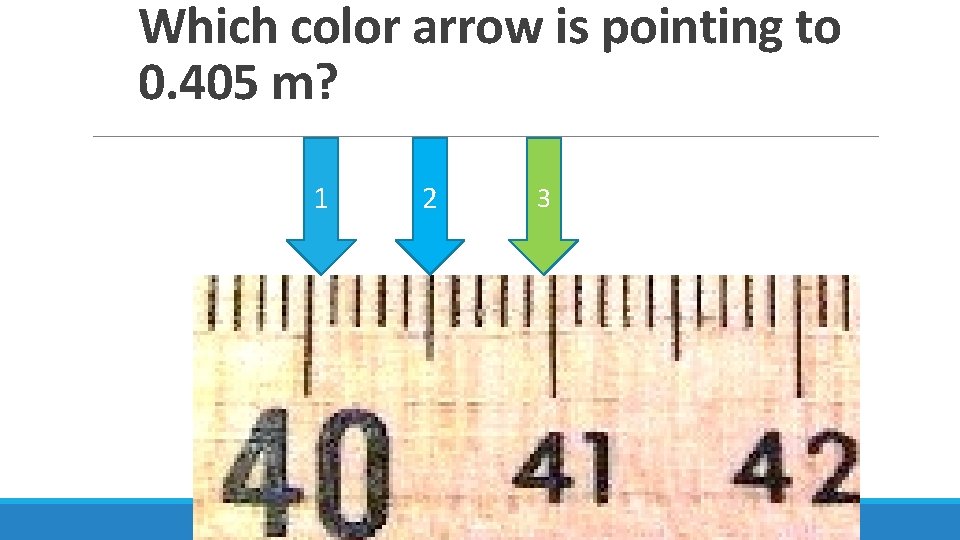
Which color arrow is pointing to 0. 405 m? 1 2 3

% Error = actual – measured x 100 A student measures the mass of an object to be 10. 2 g, but it’s actually 10. 5 g. What was his % error?

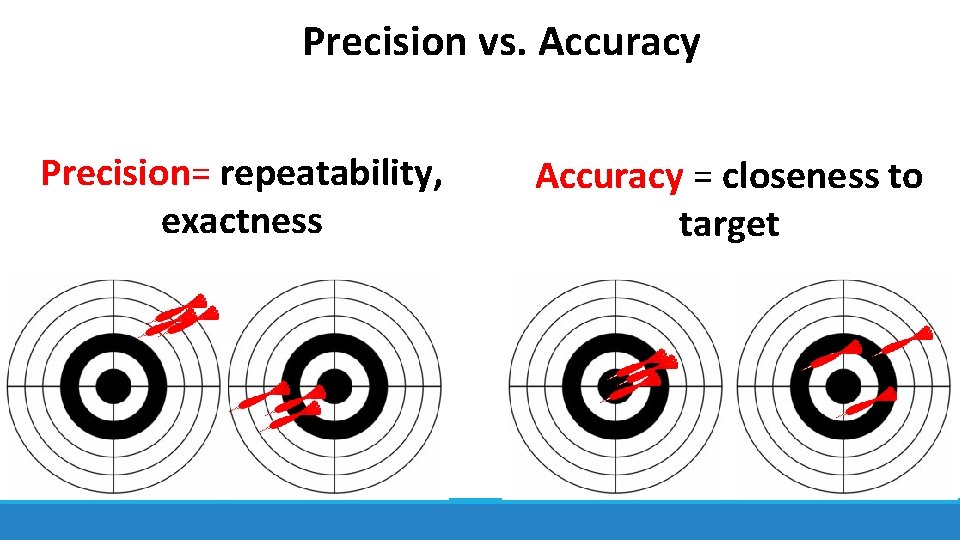
Precision vs. Accuracy Precision= repeatability, exactness Accuracy = closeness to target

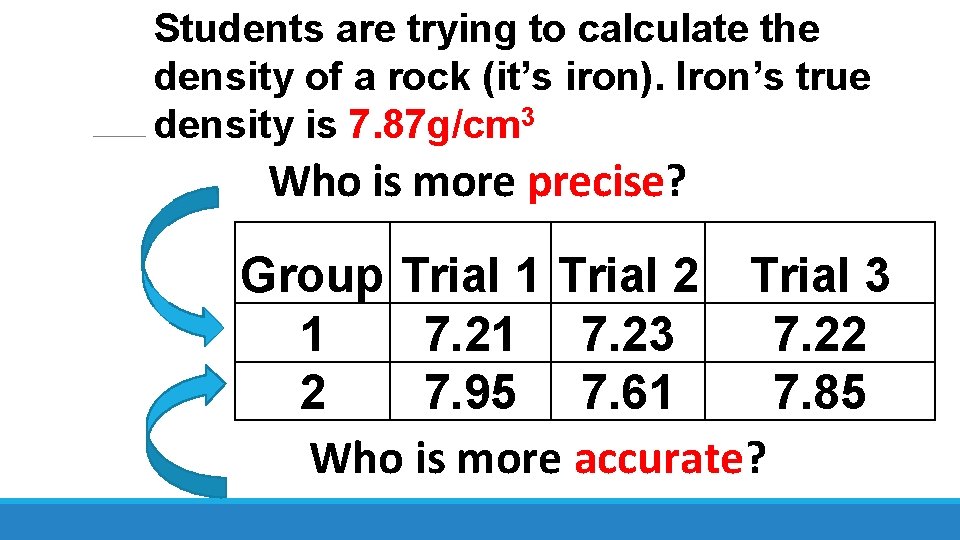
Students are trying to calculate the density of a rock (it’s iron). Iron’s true density is 7. 87 g/cm 3 Who is more precise? Group Trial 1 Trial 2 Trial 3 1 7. 23 7. 22 2 7. 95 7. 61 7. 85 Who is more accurate?

How many cm from 100 cm? your desk to the gym? 1, 000 cm? 10, 000 cm? How many atoms are in your eye? 60, 200, 000, 000 atoms! Who has time to write all that? !

Scientific Notation ◦Quick and easy way to write really big and really small #’s ◦ 10, 000 cm 1. 0 x 4 10 cm ◦ 60, 200, 000, 000 atoms! ◦ 6. 02 x 1023 atoms

Scientific notation For very big things, move the decimal to the front and count! Example: 1, 000. 00 Estimated grains of sand on Earth: 4, 000, 000, 000! =4 x 1021

Scientific notation For very small things, move the decimal to the back, count and add a negative symbol! Example: 0. 00000023

Ways to Write in Scientific Notation 1, 200, 000= 6 1. 2 x 10 1. 2 EE 6 1. 2 e+6 0. 0030= -3 3. 0 x 10 3. 0 EE-3 3. 0 e-6

Using your calculator Find the “EE” button, or “EXP” button, or “ 10 xn” button

Maintaining the “Proper” number of digits • “Significant Figures” or reliable numbers • If I use a meter stick to measure my height, I can’t report it as 160. 8987993 cm! • Watching Sig Figs is a way to maintain measurement integrity

Sig Figs in a measurement are limited by the precision of the instrument you use They are numbers that are reliably measured Hey! I’m important too! 1 2 3 4 5 5 6 7 8 9 10 10

Can you figure out how many significant figures (measured digits) each of the following has? 4 sig figs 1. 1234 2. 0. 6034 4 sig figs 3. 12, 700 4. 12, 700. 00 7 sig figs 5. 0. 000983 3 sig figs 6. 123300. 9 7 23 4 7. 6. 023 x 10 8. 0. 005600 4 1 9. 10000000 10. 2. 0 x 10 -3 2

Rules of Sig. Figs 1. Non-zeros are significant -1, 2, 3, 4, 5, 6, 7, 8, 9 How many SF in 357? 3 SF

Rules of Sig. Figs 2. Zeros between non-zeroes are always significant. Ex. 3, 105 How many SF in 4. 109? 4 SF

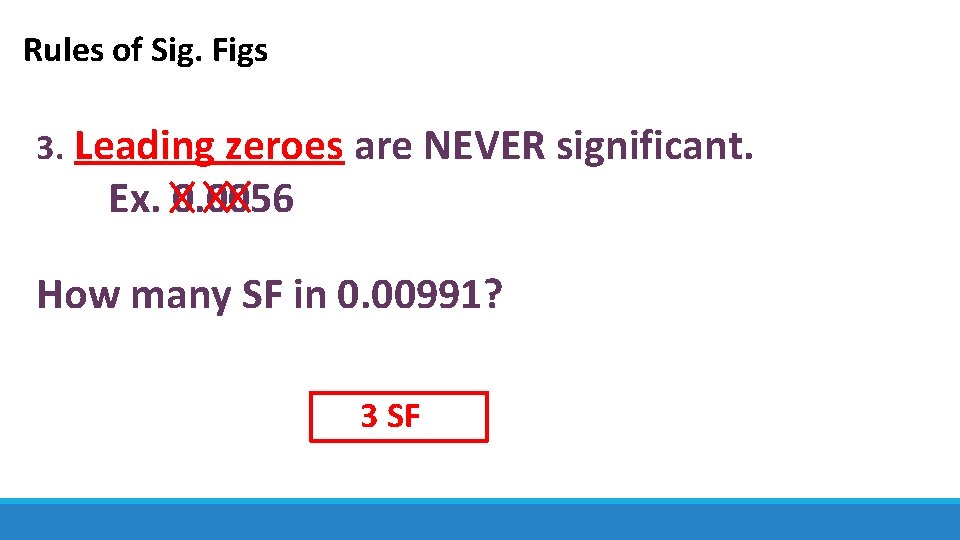
Rules of Sig. Figs 3. Leading zeroes are NEVER significant. Ex. 0. 0056 How many SF in 0. 00991? 3 SF

Rules of Sig. Figs 4. Ending zeros as placeholders are NOT significant. Ø Can remove placeholder zeros by putting in sci. notation. Ex. 905, 000 = 9. 07 x 105 = 3 SF 5. Ending zeros in a decimal ARE significant (measured) Ex. How many SF in 0. 002040? = 2. 040 x 10 -3 = 4 SF

Calculating w/Sig. Figs (Rounding Rules) Multiplying / Dividing: answer should have as many SF’s as your least precise measurement 1) 3. 2 x 4. 9999= 15. 99968 16 2) 100 x 6. 821 = 682. 1 700

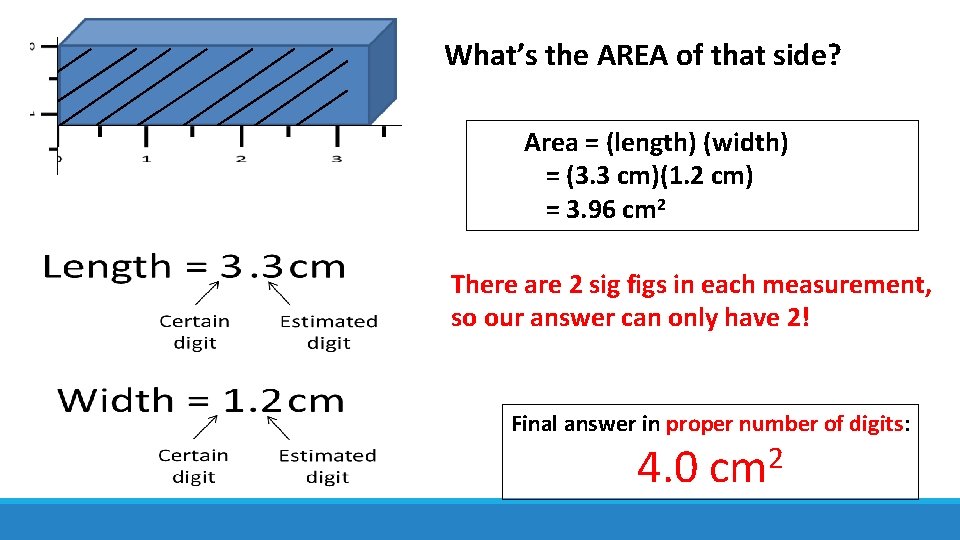
What’s the AREA of that side? Area = (length) (width) = (3. 3 cm)(1. 2 cm) = 3. 96 cm 2 There are 2 sig figs in each measurement, so our answer can only have 2! Final answer in proper number of digits: 2 4. 0 cm

Calculating w/Sig. Figs (Rounding Rules) When multiplying / dividing, answer should have as many SF’s as your least precise measurement 1) 3. 2 x 4. 9999= 15. 99968 16 2) 100 x 6. 821 = 682. 1 700

Calculating w/Sig. Figs (Rounding Rules) When adding / subtracting, answer should have as many decimal places as the measurement with the least number of decimal places 1) 3. 2 + 4. 9999= 8. 1999 8. 2 2) 100 + 6. 821 = 106. 821 107

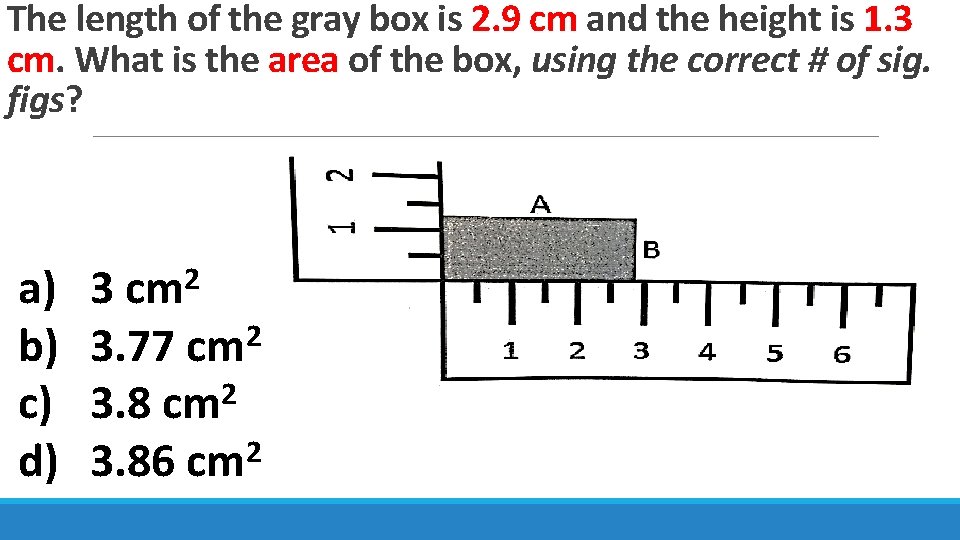
The length of the gray box is 2. 9 cm and the height is 1. 3 cm. What is the area of the box, using the correct # of sig. figs? a) b) c) d) 3 cm 2 2 3. 77 cm 3. 8 cm 2 2 3. 86 cm

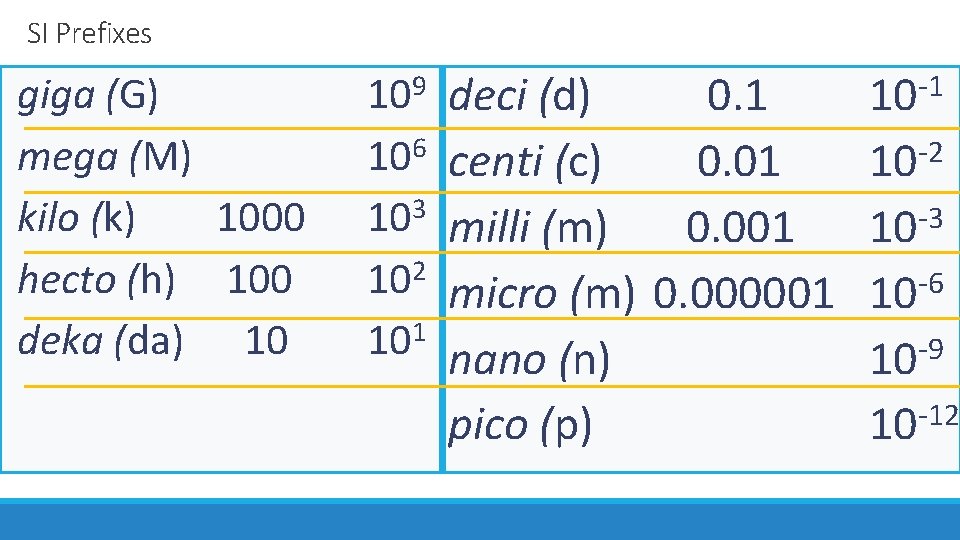
SI Prefixes giga (G) mega (M) kilo (k) 1000 hecto (h) 100 deka (da) 10 deci (d) 0. 1 106 centi (c) 0. 01 103 milli (m) 0. 001 2 10 micro (m) 0. 000001 101 nano (n) pico (p) 9 10 -1 10 -2 10 -3 10 10 -6 -9 10 10 -12

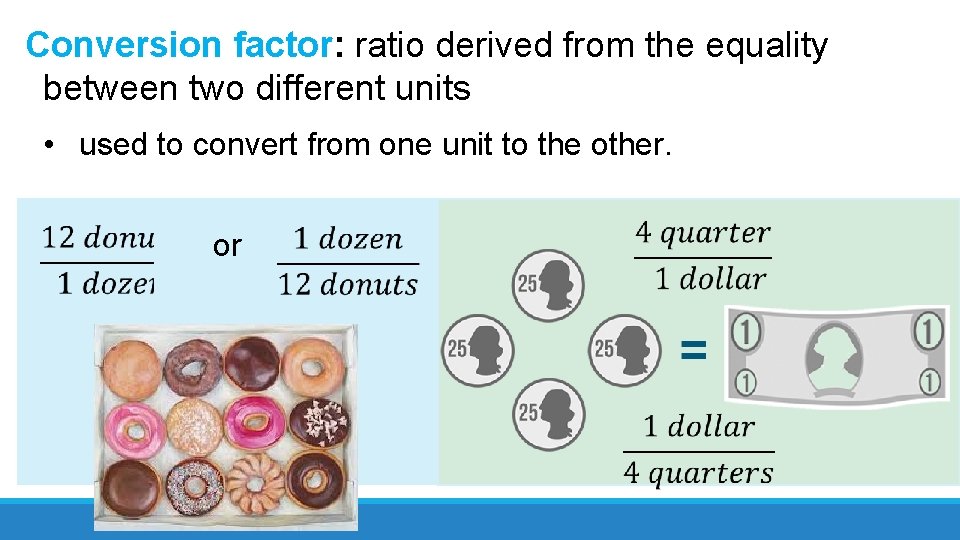
Conversion factor: ratio derived from the equality between two different units • used to convert from one unit to the other. or

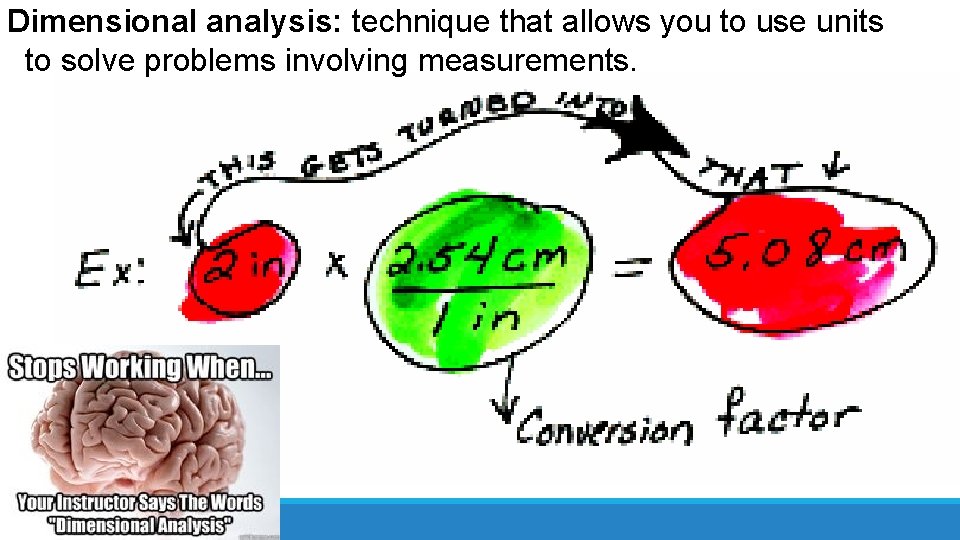
Dimensional analysis: technique that allows you to use units to solve problems involving measurements.

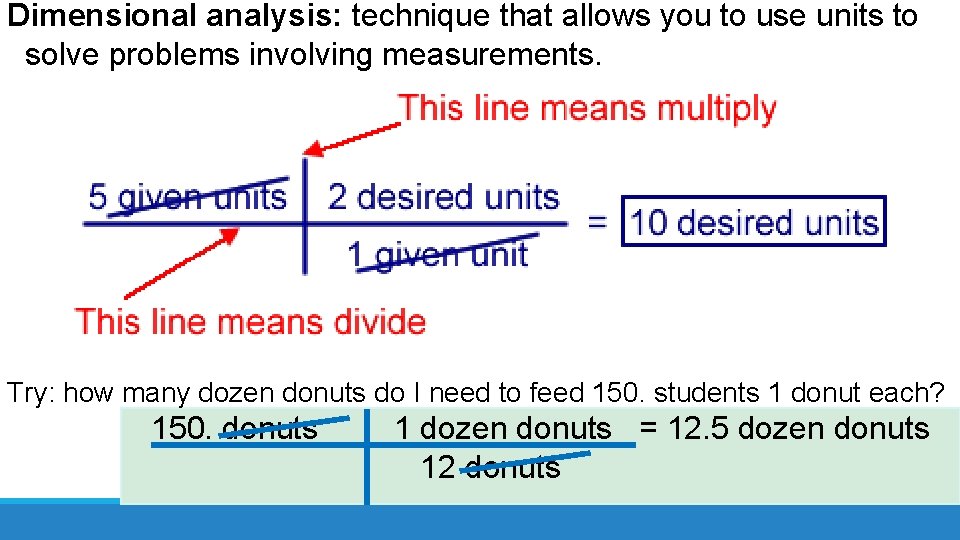
Dimensional analysis: technique that allows you to use units to solve problems involving measurements. Try: how many dozen donuts do I need to feed 150. students 1 donut each? 150. donuts 1 dozen donuts = 12. 5 dozen donuts 12 donuts