La subordination de la gomtrie lalgbre linaire analyse

La subordination de la géométrie à l’algèbre linéaire : analyse de la transposition didactique (3ème partie) Giang Ngan Nguyen, Maggy Schneider Université de Liège 1

Quelques rappels § La géométrie d’Euclide : déductive … en partie, prenant appui sur les définitions opératoires de figures géométriques mais aussi sur dessins correctement tracés qui attestent de l’existence de points ou de positions relatives de points ou de points et de droites § L’absence de nombres réels et donc de mesures est compensée par des configurations géométriques et l’idée de superposition par mouvement : Euclide peut alors traiter de segments égaux et de segments dans un rapport donné 2

La géométrie vectorielle § La géométrie d’Hilbert corrige les défauts de celle d’Euclide grâce aux axiomes de congruence, d’incidence, d’ordre et de continuité § La géométrie vectorielle apparaît comme une autre solution jugée plus accessible que la géométrie d’Hilbert § Elle correspond aux visées de la réforme des mathématiques visant à initier les élèves aux mathématiques inspirées du structuralisme § Elle bénéficiait donc d’une niche écologique porteuse à l’époque des mathématiques modernes mais qu’en est-il aujourd’hui ? 3

Niches écologiques a priori (Cissé Ba) 4

Niches écologiques a priori (Cissé Ba) 5

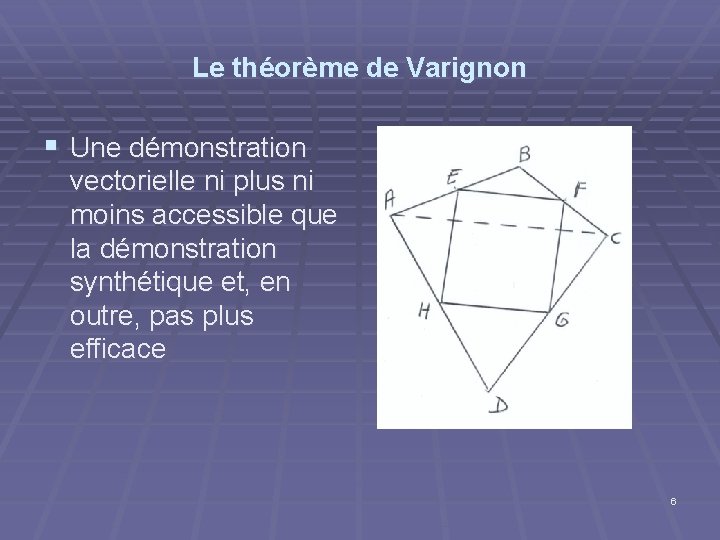
Le théorème de Varignon § Une démonstration vectorielle ni plus ni moins accessible que la démonstration synthétique et, en outre, pas plus efficace 6

Niches écologiques a priori (Cissé Ba) 7

Une niche géométrico-algébrique Analyse des enjeux d’un projet d’enseignement dans lequel on cherche à construire un formalisme qui permettrait de démontrer des propriétés de figures géométriques (plan et espace) de manière calculatoire tout en justifiant les bases de ce formalisme au départ de la géométrie d’Euclide connue des élèves 8

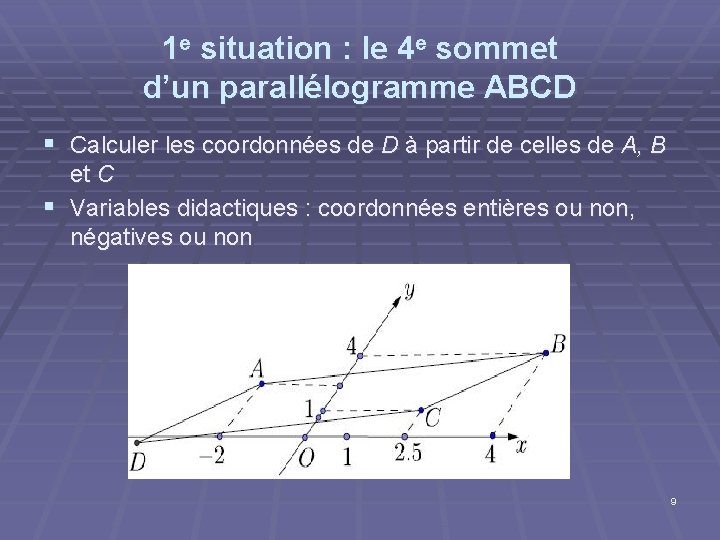
1 e situation : le 4 e sommet d’un parallélogramme ABCD § Calculer les coordonnées de D à partir de celles de A, B et C § Variables didactiques : coordonnées entières ou non, négatives ou non 9

1 e situation : le 4 e sommet d’un parallélogramme Plusieurs techniques : § Équations de droites dont on connaît un point et la pente, résolution d’un système § Utiliser 2 fois la formule du milieu d’un segment § Exploiter ce que les élèves connaissent des translations § Le démontrer via l’isométrie de triangles 10

Justification au départ de la géométrie synthétique Euclide : §Caractérisations parallélogramme §Cas d’égalité des triangles § La droite numérique comme point de départ § La bijection entre points et couples de réels § Les longueurs de segments parallèles à un axe 11

1 e situation : le 4 e sommet d’un parallélogramme § Quel que soit l’ordre des coordonnées des sommets, si ABCD est un parallélogramme non croisé, alors 12

2 e situation : un point P sur une droite AB, deux fois plus éloigné de A que de B Plusieurs techniques : § Equation de droite + expression de la distance entre deux points + système § Exploitation de triangles semblables § Exploitation des vecteurs § Projections parallèles sur les axes et exploitation du théorème de Thalès 13

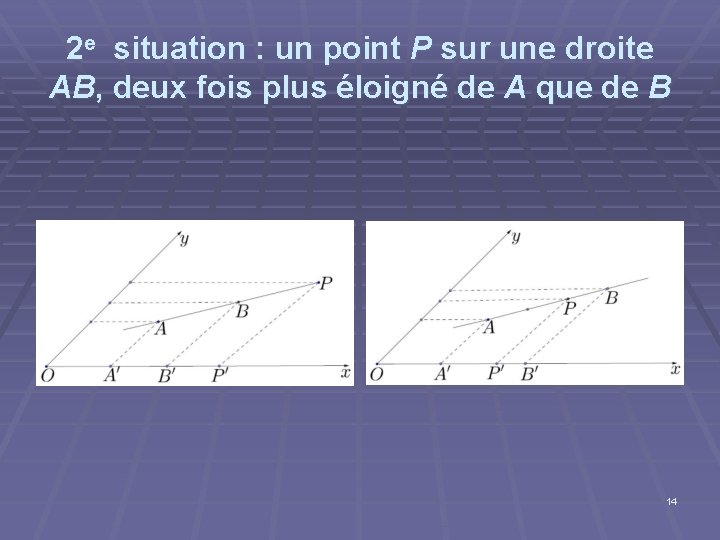
2 e situation : un point P sur une droite AB, deux fois plus éloigné de A que de B 14

2 e situation : un point P sur une droite AB, deux fois plus éloigné de A que de B 15

Questions à travailler § Comment introduire les vecteurs à partir de là ? § Quel type de repère ? Quelle géométrie impliquée ? § Portée des généralisations ? § Comment établir la bijection entre points du plan et couples de réels ? 16

Application affine et application linéaire 17

Application affine et application linéaire 18

Application affine et application linéaire 19

Application affine et application linéaire 20

Changement de repère 21

Changement de repère En comparaison avec (1), on peut constater que l’étude de l’invariance de la forme des expressions algébriques lors d’une transformation affine revient à l’étude d’un changement de repère. 22

23

Par conséquent, la pente est changée par un changement de repère. 24

Isométrie 25

Isométrie 26

Isométrie Le formule (4) présente une application affine avec le matrice M orthogonale dont le déterminant vaut 1, alors cette application est 27 une isométrie, c’est-à-dire elle conserve les distances.

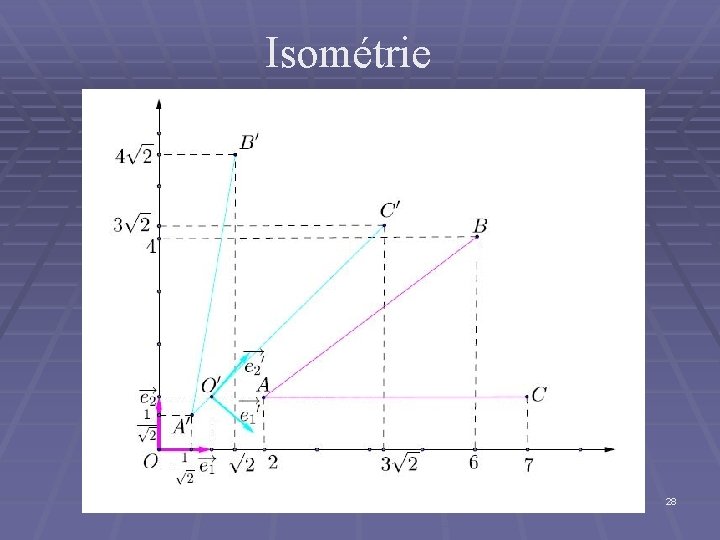
Isométrie 28

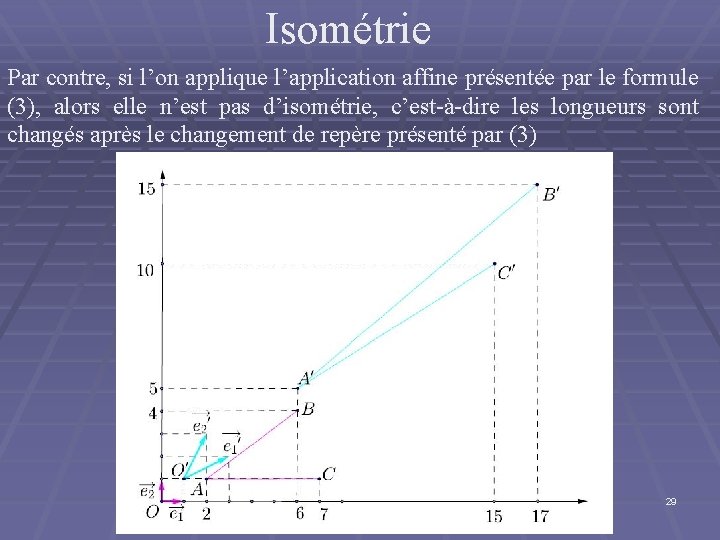
Isométrie Par contre, si l’on applique l’application affine présentée par le formule (3), alors elle n’est pas d’isométrie, c’est-à-dire les longueurs sont changés après le changement de repère présenté par (3) 29

Conclusion 30

Pourquoi les vecteurs (et opérations associées) ? Mais quelle entrée en matière pour les élèves ? Souvent, on part des translations et on évoque des questions de trajets dans un plan mais comment définir « sens » et « direction » à ce stade d’étude en dehors de la physique ? Quasiment jamais, on ne dit aux élèves qu’on cherche à exprimer des configurations géométriques et démontrer leurs propriétés de manière symbolique et calculatoire On se situe difficilement entre physique et algèbre linéaire qui est une théorie « multi-sens » 31

Pourquoi les vecteurs (et opérations associées) ? Annoncer le but : traduire des configurations géométriques au moyen des coordonnées ou vecteurs. Exemples : § Parallélogramme ABCD éventuellement « aplati » : B-A=C-D § Milieu M d’un segment EF : (E + F) / 2 Que démontre l’équivalence entre B - A = C - D et (D + B) / 2 = (A + C) / 2 ? Une situation fondamentale d’entrée dans cet univers : trouver le 4ème sommet d’un parallélogramme connaissant les 3 autres 32

Forme d’un déterminant 3 x 3 § Partir d’une définition du déterminant de n vecteurs relativement à une base en termes d’image d’une forme n-linéaire alternée § Une alternative possible, parmi d’autres, est d’étudier la compatibilité d’un système linéaire de trois équations à deux inconnues : recherche d’un critère général et non pas résolution d’un système 33

Forme d’un déterminant 3 x 3 D’une écriture « brute » à la nécessité d’une écriture « mnémotechnique » : 34

Forme d’un déterminant 3 x 3 § Intérêt d’un notation indicée : émergence historique des matrices postérieure à celle des déterminants § Caractère « multi-sens » de l’annulation d’un déterminant 3 x 3 : § § Concourance de droites Coplanarité de points Parallélisme d’une droite et d’un plan Positions relatives de trois plans (toutes sauf plans qui ont un seul point commun) § Dépendance linéaire de trois vecteurs… 35

Praxéologie « modélisation » vs praxéologie « déduction » La subordination de la géométrie à l’algèbre linéaire représente une économie de pensée énorme : e. a. les notions d’orthogonalité et de distance prennent un sens plus large et s’étendent aux espaces fonctionnels (distance chez Fréchet) mais cette subordination se paie du prix de définitions absconses et d’une absence d’articulation entre modélisation et déduction 36

Une remontée de la géométrie analytique à l’algèbre linéaire Eviter la lourdeur des calculs sur les coordonnées Notation « bipoint » vs notation « vecteur » 37

Une remontée de la géométrie analytique à l’algèbre linéaire « Vecteur : Elément d’un espace vectoriel […] (Exemples: polynôme, matrice carrée, fonction de classe C 1 sur R, progression arithmétique, éléments de R 2 ou de R 3 appelés vecteurs géométriques). […] Pendant longtemps, on appela vecteurs liés des couples de points de R 2 (ou des triplets de R 3) et vecteurs libres leurs classes modulo l’équipollence. Aujourd’hui la terminologie s’est précisée; les vecteurs liés (qui ne sont pas des vecteurs !) sont désormais appelés bipoints, le mot vecteur étant réservé aux vecteurs libres » (Bouvier et al. , Dictionnaire des mathématiques, PUF, 7 e édition de 2005) 38

Une remontée de la géométrie analytique à l’algèbre linéaire § Expressions ambiguës ou sujettes à glissemental dans l’apprentissage : vecteurs liés, vecteurs égaux, vecteurs consécutifs, vecteurs parallèles, … § D’où la nécessité de ménager un apprentissage qui permette de voir des triplets de points de manières multiples (coordonnées, variations de position, vecteur directeur, …) 39

Une remontée de la géométrie analytique à l’algèbre linéaire § Ici, les écritures vectorielles sont censées modéliser les écritures paramétriques ou cartésiennes § Dans la transposition didactique standard, le passage du vectoriel au paramétrique et au cartésien n’est pas vraiment justifié dans l’enseignement secondaire. Il manque une pièce du montage déductif : Tout espace vectoriel E de dimension finie sur un champ K est isomorphe à l’espace Kn des coordonnées (par rapport à une base donnée de E) § On observe une praxéologie « à trous » (Rouy) : on laisse tomber les maillons du schéma déductif qui semblent trop difficiles pour les élèves 40

Praxéologie « modélisation » vs praxéologie « déduction » § Dans une praxéologie « modélisation » , les tâches majeures consistent à déterminer des grandeurs, mouvements, objets géométriques, … sur base d’intuitions premières et avec les techniques les plus commodes. Ces techniques servent, en fin de parcours, à définir les objets modélisés § Dans une praxéologie « déduction » , ces mêmes définitions servent, avec des axiomes bien « choisis » , de point de départ à un développement déductif 41

En résumé § CONfigurations géométriques de base en 2 D : Parallélogramme, configurations équivalentes de trois points alignés, alignement de points, parallélisme de droites Modélisation en termes de bipoints sous forme de RELATIONS (égalités) Validée sur base de théorèmes de la géométrie élémentaire synthétique 42

Le travail à faire CONfigurations géométriques 3 D : Parallélogramme, configurations équivalentes de trois points alignés, alignement de points, parallélisme de droites, coplanarité de points Modélisation en termes de bipoints sous forme de RELATIONS (égalités), dans un ordre au choix Validation sur base de géométrie élémentaire synthétique 3 D avec identification explicite des théorèmes utilisés 43