La spcificit de la dmarche dinvestigation en mathmatiques

La spécificité de la démarche d’investigation en mathématiques Catherine Houdement, IUFM de Rouen, COPIRELEM, DIDIREM Paris 7. catherine. houdement@rouen. iufm. fr Claudine Robert, Université Joseph Fourier, Grenoble. Claudine. Robert@imag. fr Colloque La Main à la Pâte, St Etienne, 28 septembre 2005 1

Trois questions seront évoquées dans cet exposé : • La démarche d’investigation est- elle appropriée à un enseignement des mathématiques ? • La statistique : peut-on commencer en primaire ? • Quel est le statut des mathématiques rencontrées au cours des activités de La Main à la Pâte ? 2

A propos de la première question, il convient de bien distinguer : -les mathématiques construites, souvent présentées selon l’organisation définitions / théorèmes / applications On associe à cette triade les activités suivantes : abstraire / démontrer/ déduire Et on ne voit pas où se situerait une démarche d’investigation. - les mathématiques en voie de construction Laissons la parole au mathématicien Vladimir Arnold : Les mathématiques sont la branche de la physique où les expériences ne coûtent pas cher. C’est une boutade…. elle contient donc une part de vérité et une part d’exagération : 3

Les mathématiques peuvent être vues comme une branche de la physique dans une première phase de leur élaboration ou de leur apprentissage : En mathématiques comme dans les autres sciences, on commence par observer, expérimenter, pour construire un rapport de familiarité et de confiance avec des objets (ici des objets conceptuels tels les nombres, les figures, les chances). On fait des « bouts de démonstrations » . Ensuite, des années ou des siècles plus tard viennent : …. . définitions, théorèmes…questions …. observations …. qui s’organisent en théorie…. Les mathématiques ne sont pas une branche de la physique : Dans les sciences expérimentales la validation se fait par la la théorie et par l’expérience. En mathématiques, la validation ne se fait que par la démonstration. Et dans l’enseignement ? 4

Démarche d’investigation et enseignement des mathématiques 5

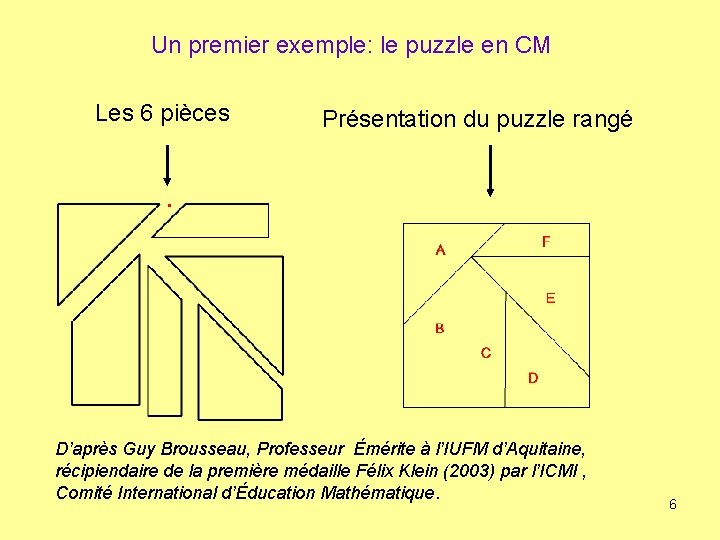
Un premier exemple: le puzzle en CM Les 6 pièces Présentation du puzzle rangé D’après Guy Brousseau, Professeur Émérite à l’IUFM d’Aquitaine, récipiendaire de la première médaille Félix Klein (2003) par l’ICMI , Comité International d’Éducation Mathématique. 6

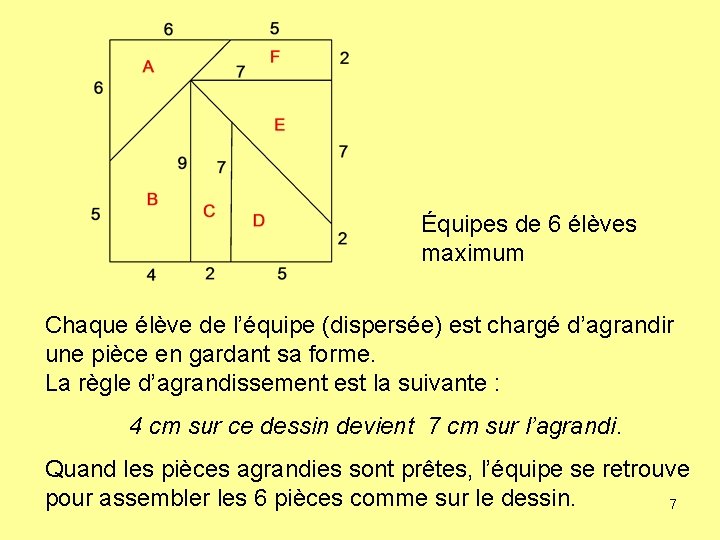
Équipes de 6 élèves maximum Chaque élève de l’équipe (dispersée) est chargé d’agrandir une pièce en gardant sa forme. La règle d’agrandissement est la suivante : 4 cm sur ce dessin devient 7 cm sur l’agrandi. Quand les pièces agrandies sont prêtes, l’équipe se retrouve pour assembler les 6 pièces comme sur le dessin. 7

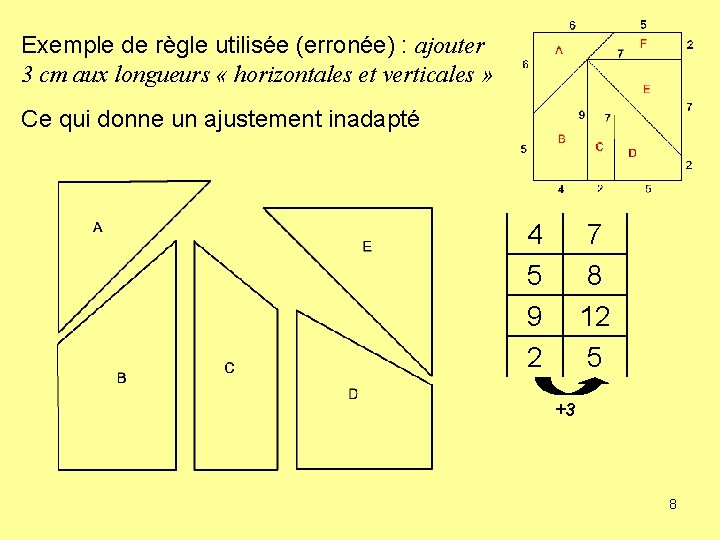
Exemple de règle utilisée (erronée) : ajouter 3 cm aux longueurs « horizontales et verticales » Ce qui donne un ajustement inadapté 4 5 9 2 7 8 12 5 +3 8

Une autre règle inférée par les élèves 7 obtenu comme 4 x 2 - 1 4 8 5 7 15 9 9 17 a ax 2 - 1 . Là encore l’ajustement ne donne pas un carré. Les élèves commencent à penser que c’est une tâche impossible…. La question évolue. Comment contrôler les calculs sur les longueurs dans la perspective d’obtenir de bons assemblages : un carré en assemblant les 6 pièces…. . ? 9

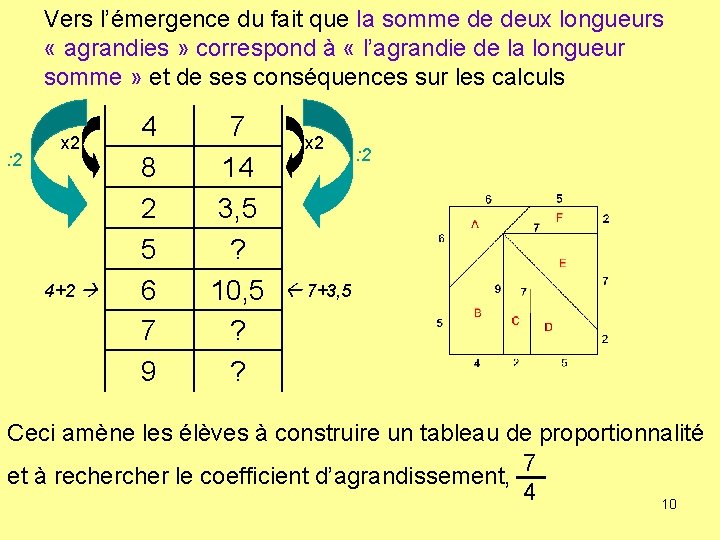
Vers l’émergence du fait que la somme de deux longueurs « agrandies » correspond à « l’agrandie de la longueur somme » et de ses conséquences sur les calculs : 2 x 2 4+2 4 8 2 5 6 7 9 7 14 3, 5 ? 10, 5 ? ? x 2 : 2 7+3, 5 Ceci amène les élèves à construire un tableau de proportionnalité 7 et à recher le coefficient d’agrandissement, 4 10

Ainsi la situation est contrainte par le professeur pour que les élèves, en agissant sur les pièces, puissent apprendre. Visées du professeur, à moyen terme * Mettre en défaut le modèle additif (spontané) * Construire un modèle proportionnel, reconnaître sa pertinence pour l’agrandissement Démarche des élèves Les élèves doivent progressivement mettre au point un protocole de construction qui résiste à l’ajustement. Une première validation est matérielle : les pièces du puzzle sont choisies pour garantir -presque toujours- un mauvais ajustement si l’agrandissement n’est pas licite. 11

Second exemple : des poules et des lapins…. au cycle 3 Des poules et des lapins Jojo, un peu farfelu, compte les têtes et trouve 8 têtes. Puis il compte les pattes et trouve 26 pattes. Saurais tu trouver le nombre de poules et celui de lapins? Des voitures et des motos Jojo compte 19 véhicules et 52 roues. Combien de voitures? Combien de motos ? L’élève n’a pas appris de technique pour ces problèmes (système de 2 équations à 2 inconnues): il doit construire un protocole de résolution qui nécessite l’insertion d’une hypothèse, par exemple, le nombre de lapins. 12

Quelques exemples de productions d’élèves de cycle 3 Réponse attendue pour 8 têtes et 26 pattes : 5 lapins et 3 poules Agnès CE 2 13

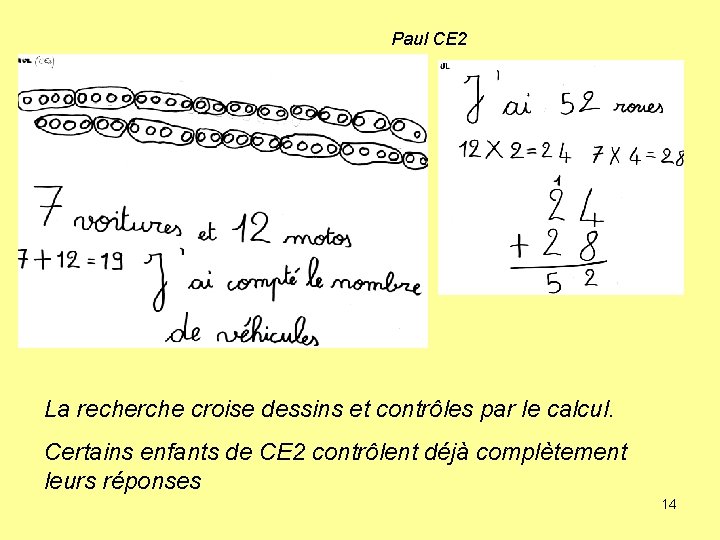
Paul CE 2 La recherche croise dessins et contrôles par le calcul. Certains enfants de CE 2 contrôlent déjà complètement leurs réponses 14

CM : réponse exacte 12 motos et 7 voitures pour 19 véhicules et 52 roues Le contrôle des réponses (nombre de roues et nombre de véhicules) n’est pas assuré au CM. La diversité des réponses ci-dessus est prétexte à débat, tranché 15 par le retour au texte de départ (nombre de véhicules).

Conclusion de la première partie La démarche d’investigation intervient en mathématiques, en particulier dans les problèmes de recherche, numériques ou géométriques. Mais les environnements des problèmes sont beaucoup plus contraints par le professeur pour amener l’élève au plus près de la connaissance visée. En mathématiques, trois types de connaissances : « connaissances en actes » ; langages; preuves et théories. Le langage mathématique est spécifique. Il existe aussi en mathématiques plusieurs niveaux de preuve : ce niveau change avec la nature des objets sur lesquels elle s’exerce et les connaissances des ‘acteurs’ (élèves, étudiants…). 16

La géométrie de l’école est particulièrement propice à une démarche expérimentale. La validation est souvent matérielle, médiée par les instruments. Elle deviendra virtuelle (Cabri…) , puis progressivement théorique (démonstrations). Et la statistique ? 17

Enseigner la statistique 18

Edgar Morin. Dans son ouvrage « les 7 savoirs nécessaires à l’éducation » , un de ces savoirs est répertorié sous le titre « affronter l’incertitude » . Statistiques du citoyen : un enjeu éducatif pour tous les pays. En primaire, on ne va pas aborder la statistique, mais on peut entrer dans le monde de l’aléatoire. On commence par faire des expériences d’où se forge une intuition juste. On construit des images mentales propices à une conceptualisation ultérieure. Pour le professeur , voici trois éléments clés pour se lancer avec les élèves dans une sensibilisation à l’aléatoire. 19

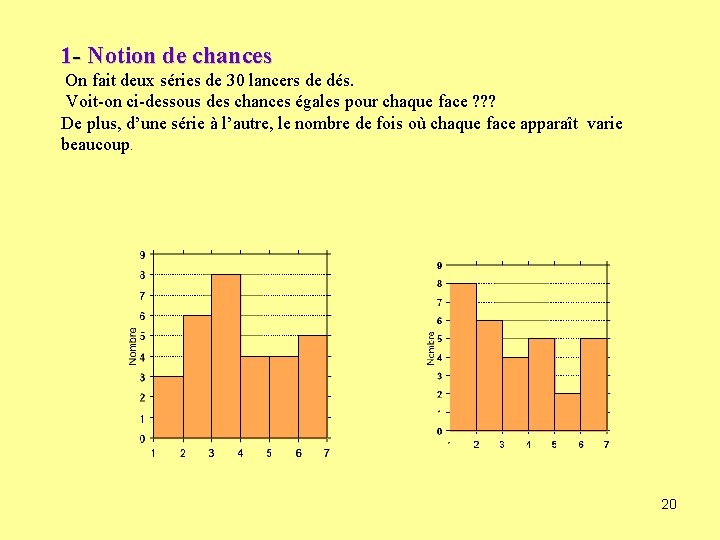
1 - Notion de chances On fait deux séries de 30 lancers de dés. Voit-on ci-dessous des chances égales pour chaque face ? ? ? De plus, d’une série à l’autre, le nombre de fois où chaque face apparaît varie beaucoup. 20

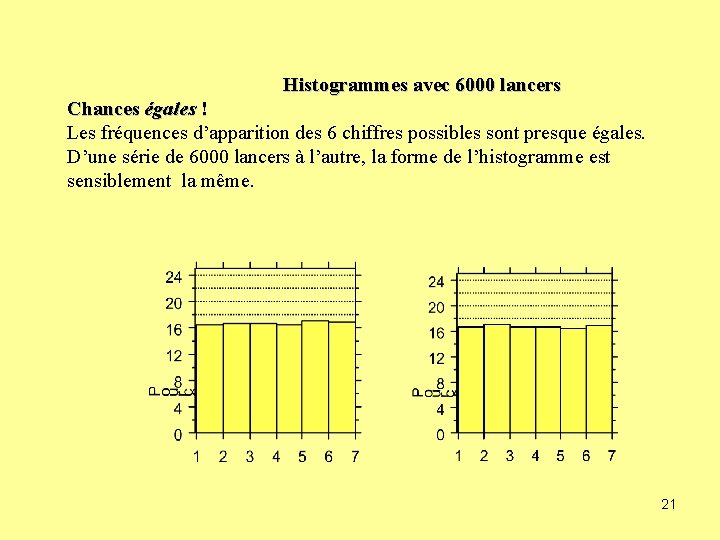
Histogrammes avec 6000 lancers Chances égales ! Les fréquences d’apparition des 6 chiffres possibles sont presque égales. D’une série de 6000 lancers à l’autre, la forme de l’histogramme est sensiblement la même. 21

Changer l’échelle du regard permet de voir apparaître des régularités Un « Théorème des grands nombres » explique l’apparition de ces régularités et permet : - en sciences sociales de passer de l’individu à la population Exemple : on peut prévoir environ 800 000 naissances par an en France, sans savoir dans quelle famille elles auront lieu. - de passer de la molécule à la mole en physique Remarque : dans la pratique de la statistique 100 est souvent déjà un grand nombre. 22

2 -Risques En statistique, on ne peut rien affirmer. Il y a toujours un risque d’erreur dans ce qu’on dit, mais on cherche à quantifier ce risque. Exemple du dé avec 2 ou 3 faces blanches , les autres noires. Comment savoir s’il y en a 2 ou 3 ? Voici les résultats de 200 lancers. On peut alors dire que c’est plutôt deux faces blanches, mais il y a un risque de se tromper et le statisticien calculera ses chances d’erreur. 23

3 -Il existe des dés électroniques • Dé : expériences réelles • Dé électronique : expériences virtuelles Les dés électroniques permettent de faire des milliers d’expériences en peu de temps. Mais si on y accède trop vite, certaines questions dont la réponse fait avancer dans le maniement de l’aléatoire ne se posent pas, ou leur réponse est cachée par la puissance de l’outil. • • En primaire, il convient de faire des expériences réelles, avec des « vrais dés » pour mieux comprendre les notions de chances égales ou inégales. Le recours par le maître à des résultats d’expériences virtuelles peut aider à stabiliser des intuitions. (on a l’analogue en géométrie avec les logiciels de géométrie dynamique) Suit la présentation de trois activités, qui font l’objet d’un texte plus détaillé sur la page de ce colloque. 24

1 -Construire des nombres On construit trois nombres à deux chiffres en utilisant des dés de telle sorte que leur somme soit la plus grande possible. • • • Les deux chiffres de chaque nombre sont obtenus en lançant un dé. L’élève place tout de suite dans la case des dizaines ou des unités le résultat du premier lancer : il est libre de son choix. Puis il complète avec le résultat du deuxième lancer. dé 1 : 5 dé 2 : 3 dé 1 : 2 dé 2 : 6 dé 1 : 3 dé 2 : 2 On a 158 comme somme, mais avec les mêmes résultats de lancers on aurait pu avoir 32 comme troisième nombre et la somme aurait été égale à 147. Cette activité numérique qui utilise les dés est aussi l’occasion de récolter des résultats et de les confronter aux idées a priori des élèves. 25

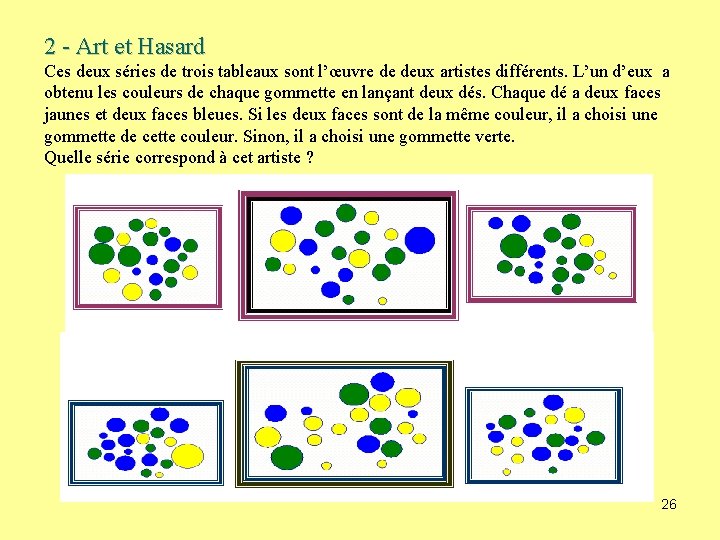
2 - Art et Hasard Ces deux séries de trois tableaux sont l’œuvre de deux artistes différents. L’un d’eux a obtenu les couleurs de chaque gommette en lançant deux dés. Chaque dé a deux faces jaunes et deux faces bleues. Si les deux faces sont de la même couleur, il a choisi une gommette de cette couleur. Sinon, il a choisi une gommette verte. Quelle série correspond à cet artiste ? 26

3 - La courte paille • • • Choisi aujourd’hui, pas choisi demain ? Équilibre. . . à long terme. Choix à la courte paille et au dé : dispositifs comparables ? Ces trois activités peuvent être discutées en famille (formation des parents !). Exemples transposables à d’autres situations et qu’on peut approfondir à des niveaux ultérieurs. 27

Au cycle 3 Une introduction au monde de l’aléatoire permet de : -Partager un questionnement -Mettre en commun des résultats. Les savoirs visés sont: - la notion de chances : liée à la répétition - les dés n’ont pas de mémoire (il serait difficile de le faire comprendre en n’utilisant que des dés électroniques). - les possibilités et chances égales (ce n’est pas parce qu’une expérience peut mener à des résultats distincts que ceux -ci ont des chances égales) Atteindre ces savoirs sera un grand progrès ! Langage parlé : spontané (pas de formalisation théorique)/ langage graphique Ecrit : cahier d’expériences indispensable pour qu’il y ait progression. 28

Conclusion 29

(1) Mathématiques et démarche d’investigation Deux domaines où la démarche expérimentale est particulièrement constitutive du sens : la géométrie, science de l’espace et la statistique, science de l’aléatoire. Mais la démarche existe aussi dans le numérique. Pourtant il existe dans ces domaines des théories de référence : géométrie axiomatique pour l’un et probabilités pour l’autre… L’expérimentation est fondamentale dans les sciences (mathématiques comprises), même si la nature des objets (matériels, virtuels, mentaux, conceptuels) sur lesquels s’exerce cette expérimentation peut dépendre du domaine. 30

(2) Mathématiques dans les situations scientifiques de la Main à la Pâte Un exemple : le voyage de Marco Polo http: //www. mapmonde. org/marcopolo/ Comment Marco Polo s’y est-il pris pour être sûr de retrouver le trésor lors de son prochain passage ? Un échange entre élèves permet de dégager rapidement la nécessité d’une boussole. 31

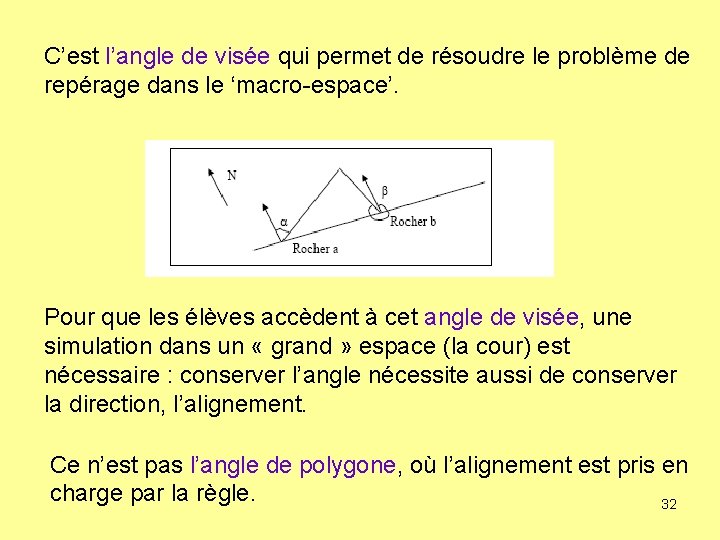
C’est l’angle de visée qui permet de résoudre le problème de repérage dans le ‘macro-espace’. Pour que les élèves accèdent à cet angle de visée, une simulation dans un « grand » espace (la cour) est nécessaire : conserver l’angle nécessite aussi de conserver la direction, l’alignement. Ce n’est pas l’angle de polygone, où l’alignement est pris en charge par la règle. 32

Les élèves sont ainsi confrontés à une des conceptions de l’angle (angle de visée), conception historiquement fondatrice du concept d’angle. Ils sont aussi confrontés à sa mesure, hors programme cycle 3 ; plus exactement ils apprennent à utiliser un instrument , la boussole. Ils pourront aussi « rencontrer l’angle » quand ils s’intéresseront à la période d’un pendule et cheront à faire varier angle de départ, longueur… La conception est alors l’angle de rotation. L’angle est ainsi outil dans des problèmes scientifiques , avant de devenir objet d’étude dans les mathématiques. 33

Ainsi des concepts commencent à être fréquentés, sans être considérés comme définitivement appris. L’élève rencontre un objet sous de multiples conceptions. Il accumule ainsi des expériences, constitutives de savoirs futurs. 34